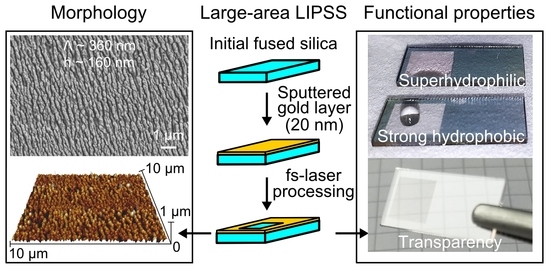
Large-Area Fabrication of Laser-Induced Periodic Surface Structures on Fused Silica Using Thin Gold Layers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Laser Processing
2.3. Characterization
3. Results and Discussion
3.1. Single-Spot Investigation
3.2. Large-Area Fabrication of HSFL
3.3. Characterization of Surface Properties
3.3.1. Surface Chemistry
3.3.2. Wettability
3.3.3. Optical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barthlott, W.; Neinhuis, C. Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 1997, 202, 1–8. [Google Scholar] [CrossRef]
- Bernhard, C.G. Structural and functional adaptation in a visual system. Endeavour 1967, 26, 79–84. [Google Scholar]
- Bonse, J.; Höhm, S.; Kirner, S.V.; Rosenfeld, A.; Krüger, J. Laser-induced periodic surface structures—A scientific evergreen. IEEE J. Select. Top. Quant. Electron. 2017, 23, 9000615. [Google Scholar] [CrossRef]
- Vorobyev, A.Y.; Guo, C. Direct femtosecond laser surface nano/microstructuring and its applications. Laser Photon. Rev. 2013, 7, 385–407. [Google Scholar] [CrossRef]
- Liu, H.; Lin, W.; Hong, M. Surface coloring by laser irradiation of solid substrates. APL Photonics 2019, 4, 051101. [Google Scholar] [CrossRef] [Green Version]
- Bonse, J.; Krüger, J.; Höhm, S.; Rosenfeld, A. Femtosecond laser-induced periodic surface structures. J. Laser Appl. 2012, 24, 042006. [Google Scholar] [CrossRef]
- Reif, J.; Costache, F.; Henyk, M.; Pandelov, S.V. Ripples revisited: Non-classical morphology at the bottom of femtosecond laser ablation craters in transparent dielectrics. Appl. Surf. Sci. 2002, 197, 891–895. [Google Scholar] [CrossRef]
- Höhm, S.; Rosenfeld, A.; Krüger, J.; Bonse, J. Femtosecond laser-induced periodic surface structures on silica. J. Appl. Phys. 2012, 112, 014901. [Google Scholar] [CrossRef]
- Gräf, S.; Kunz, C.; Müller, F.A. Formation and Properties of Laser-Induced Periodic Surface Structures on Different Glasses. Materials 2017, 10, 933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gräf, S.; Kunz, C.; Engel, S.; Derrien, T.J.Y.; Müller, F.A. Femtosecond laser-induced periodic surface structures on fused silica: The impact of the initial substrate temperature. Materials 2018, 11, 1340. [Google Scholar] [CrossRef] [Green Version]
- Rosenfeld, A.; Rohloff, M.; Höhm, S.; Krüger, J.; Bonse, J. Formation of laser-induced periodic surface structures on fused silica upon multiple parallel polarized double-femtosecond-laser-pulse irradiation sequences. Appl. Surf. Sci. 2012, 258, 9233–9236. [Google Scholar] [CrossRef]
- Schwarz, S.; Rung, S.; Hellmann, R. Generation of laser-induced periodic surface structures on transparent material-fused silica. Appl. Phys. Lett. 2016, 108, 181607. [Google Scholar] [CrossRef]
- Seifert, G.; Kaempfe, M.; Syrowatka, F.; Harnagea, C.; Hesse, D.; Graener, H. Self-organized structure formation on the bottom of femtosecond laser ablation craters in glass. Appl. Phys. A 2005, 81, 799–803. [Google Scholar] [CrossRef]
- Sipe, J.E.; Young, J.F.; Preston, J.S.; van Driel, H.M. Laser-induced periodic surface structure. I. Theory. Phys. Rev. B 1983, 27, 1141–1154. [Google Scholar] [CrossRef]
- Varlamova, O.; Costache, F.; Reif, J.; Bestehorn, M. Self-organized pattern formation upon femtosecond laser ablation by circularly polarized light. Appl. Surf. Sci. 2006, 252, 4702–4706. [Google Scholar] [CrossRef]
- Rudenko, A.; Colombier, J.P.; Höhm, S.; Rosenfeld, A.; Krüger, J.; Bonse, J.; Itina, T.E. Spontaneous periodic ordering on the surface and in the bulk of dielectrics irradiated by ultrafast laser: A shared electromagnetic origin. Sci. Rep. 2017, 7, 12306. [Google Scholar] [CrossRef]
- Schwarz, S.; Rung, S.; Hellmann, R. One-dimensional low spatial frequency LIPSS with rotating orientation on fused silica. Appl. Surf. Sci. 2017, 411, 113–116. [Google Scholar] [CrossRef]
- Schwarz, S.; Rung, S.; Esen, C.; Hellmann, R. Surface Plasmon Polariton Triggered Generation of 1D-Low Spatial Frequency LIPSS on Fused Silica. Appl. Sci. 2018, 8, 1624. [Google Scholar] [CrossRef] [Green Version]
- Papadopoulos, A.; Skoulas, E.; Mimidis, A.; Perrakis, G.; Kenanakis, G.; Tsibidis, G.D.; Stratakis, E. Biomimetic omnidirectional antireflective glass via direct ultrafast laser nanostructuring. Adv. Mater. 2019, 31, 1901123. [Google Scholar] [CrossRef]
- Kostal, E.; Stroj, S.; Kasemann, S.; Matylitsky, V.; Domke, M. Fabrication of biomimetic fog-collecting superhydrophilic-superhydrophobic surface micropatterns using femtosecond lasers. Langmuir 2018, 34, 2933–2941. [Google Scholar] [CrossRef]
- Kunz, C.; Müller, F.A.; Gräf, S. Multifunctional Hierarchical Surface Structures by Femtosecond Laser Processing. Materials 2018, 11, 789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, S.-Z.; Dou, H.-Q.; Sun, K.; Ye, Y.-Y.; Li, Z.; Wang, H.-J.; Liao, W.; Liu, H.; Miao, X.-X.; Yuan, X.-D.; et al. Scan speed and fluence effects in femtosecond laser induced micro/nano-structures on the surface of fused silica. J. Non-Cryst. Solids 2018, 492, 56–62. [Google Scholar] [CrossRef]
- Lin, Y.; Han, J.; Cai, M.; Liu, W.; Luo, X.; Zhang, H.; Zhong, M. Durable and robust transparent superhydrophobic glass surfaces fabricated by a femtosecond laser with exceptional water repellency and thermostability. J. Mater. Chem. A 2018, 6, 9049–9056. [Google Scholar] [CrossRef]
- Yin, K.; Wang, C.; Duan, J.; Guo, C.L. Femtosecond laser-induced periodic surface structural formation on sapphire with nanolayered gold coating. Appl. Phys. A Mater. Sci. Process. 2016, 122, 834. [Google Scholar] [CrossRef]
- Wen, Q.; Wang, H.; Cheng, G.; Jiang, F.; Lu, J.; Xu, X. Improvement of ablation capacity of sapphire by gold film-assisted femtosecond laser processing. Opt. Laser Eng. 2020, 128, 106007. [Google Scholar] [CrossRef]
- Farid, N.; Nieto, D.; O’Connor, G.M. Thin film enabling sub-250 nm nano-ripples on glass by low fluence IR picosecond laser irradiation. Opt. Laser Technol. 2018, 108, 26–31. [Google Scholar] [CrossRef]
- Wang, L.; Cao, X.-W.; Abid, M.I.; Li, Q.-K.; Tian, W.-J.; Chen, Q.-D.; Juodkazis, S.; Sun, H.-B. Nano-ablation of silica by plasmonic surface wave at low fluence. Opt. Lett. 2017, 42, 4446–4449. [Google Scholar] [CrossRef] [Green Version]
- Feng, P.; Jiang, L.; Li, X.; Rong, W.L.; Zhang, K.H.; Cao, Q. Gold-film coating assisted femtosecond laser fabrication of large-area, uniform periodic surface structures. Appl. Opt. 2015, 54, 1314–1319. [Google Scholar] [CrossRef]
- Liu, J.M. Simple technique for measurements of pulsed Gaussian-beam spot sizes. Opt. Lett. 1982, 7, 196–198. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Matthias, E.; Reichling, M.; Siegel, J.; Kading, O.W.; Petzoldt, S.; Skurk, H.; Bizenberger, P.; Neske, E. The influence of thermal-diffusion on laser-ablation of metal-films. Appl. Phys. A-Mater. Sci. Process. 1994, 58, 129–136. [Google Scholar] [CrossRef]
- Krüger, J.; Dufft, D.; Koter, R.; Hertwig, A. Femtosecond laser-induced damage of gold films. Appl. Surf. Sci. 2007, 253, 7815–7819. [Google Scholar] [CrossRef]
- Güdde, J.; Hohlfeld, J.; Müller, J.G.; Matthias, E. Damage threshold dependence on electron-phonon coupling in Au and Ni films. Appl. Surf. Sci. 1998, 127, 40–45. [Google Scholar] [CrossRef]
- Stuart, B.C.; Feit, M.D.; Herman, S.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Optical ablation by high-power short-pulse lasers. J. Opt. Soc. Am. B-Opt. Phys. 1996, 13, 459–468. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.B.; Lee, S.H. Thermal boundary resistance effect on non-equilibrium energy transport in metal-dielectric thin films heated by femtosecond pulse lasers. Mater. Trans. 2011, 52, 1492–1499. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, A.; Reddy, P. Role of electron-phonon coupling in thermal conductance of metal-nonmetal interfaces. Appl. Phys. Lett. 2004, 84, 4768–4770. [Google Scholar] [CrossRef]
- Derrien, T.J.Y.; Koter, R.; Krüger, J.; Höhm, S.; Rosenfeld, A.; Bonse, J. Plasmonic formation mechanism of periodic 100-nm-structures upon femtosecond laser irradiation of silicon in water. J. Appl. Phys. 2014, 116, 074902. [Google Scholar] [CrossRef]
- Nieto, D.; Cambronero, F.; Flores-Arias, M.T.; Farid, N.; O’Connor, G.M. Aluminum thin film enhanced IR nanosecond laser-induced frontside etching of transparent materials. Opt. Laser Eng. 2017, 88, 233–242. [Google Scholar] [CrossRef]
- Höhm, S.; Rosenfeld, A.; Krüger, J.; Bonse, J. Femtosecond diffraction dynamics of laser-induced periodic surface structures on fused silica. Appl. Phys. Lett. 2013, 102, 054102. [Google Scholar] [CrossRef]
- Petite, G.; Guizard, S.; Martin, P.; Quéré, F. Comment on Ultrafast electron dynamics in femtosecond optical breakdown of dielectrics. Phys. Rev. Lett. 1999, 83, 5182. [Google Scholar] [CrossRef]
- Richter, S.; Heinrich, M.; Doring, S.; Tunnermann, A.; Nolte, S.; Peschel, U. Nanogratings in fused silica: Formation, control, and applications. J. Laser Appl. 2012, 24. [Google Scholar] [CrossRef]
- Richter, S.; Jia, F.; Heinrich, M.; Doring, S.; Peschel, U.; Tunnermann, A.; Nolte, S. The role of self-trapped excitons and defects in the formation of nanogratings in fused silica. Opt. Lett. 2012, 37, 482–484. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, S.; Rung, S.; Esen, C.; Hellmann, R. Homogeneous Low Spatial Frequency LIPSS on Dielectric Materials Generated by Beam-Shaped Femtosecond Pulsed Laser Irradiation. J. Laser Micro Nanoeng. 2018, 13, 90–94. [Google Scholar] [CrossRef]
- Möhl, A.; Kaldun, S.; Kunz, C.; Müller, F.A.; Fuchs, U.; Gräf, S. Tailored focal beam shaping and its application in laser material processing. J. Laser Appl. 2020, 31, 042019. [Google Scholar]
- Varkentina, N.; Dussauze, M.; Royon, A.; Ramme, M.; Petit, Y.; Canioni, L. High repetition rate femtosecond laser irradiation of fused silica studied by Raman spectroscopy. Opt. Mater. Express 2016, 6, 79–90. [Google Scholar] [CrossRef]
- Salleo, A.; Taylor, S.T.; Martin, M.C.; Panero, W.R.; Jeanloz, R.; Sands, T.; Génin, F.Y. Laser-driven formation of a high-pressure phase in amorphous silica. Nat. Mater. 2003, 2, 796–800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reichman, W.; Chan, J.W.; Krol, D.M. Confocal fluorescence and Raman microscopy of femtosecond laser-modified fused silica. J. Phys. Condens. Matter 2003, 15, S2447–S2456. [Google Scholar] [CrossRef]
- De Michele, V.; Royon, M.; Marin, E.; Alessi, A.; Morana, A.; Boukenter, A.; Cannas, M.; Girard, S.; Ouerdane, Y. Near-IR- and UV-femtosecond laser waveguide inscription in silica glasses. Opt. Mater. Express 2019, 9, 4624–4633. [Google Scholar] [CrossRef]
- Rhinow, D.; Weber, N.E.; Turchanin, A. Atmospheric pressure, temperature-induced conversion of organic monolayers into nanocrystalline graphene. J. Phys. Chem. C 2012, 116, 12295–12303. [Google Scholar] [CrossRef]
- Sharma, B.; Frontiera, R.R.; Henry, A.I.; Ringe, E.; Van Duyne, R.P. SERS: Materials, applications, and the future. Mater. Today 2012, 15, 16–25. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Kietzig, A.M.; Hatzikiriakos, S.G.; Englezos, P. Patterned superhydrophobic metallic surfaces. Langmuir 2009, 25, 4821–4827. [Google Scholar] [CrossRef] [PubMed]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Raguin, D.H.; Morris, G.M. Antireflection structured surfaces for the infrared spectral region. Appl. Opt. 1993, 32, 1154–1167. [Google Scholar] [CrossRef]
- Grann, E.B.; Moharam, M.G.; Pommet, D.A. Optimal design for antireflective tapered two-dimensional subwavelength grating structures. J. Opt. Soc. Am. A 1995, 12, 333–339. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kunz, C.; Engel, S.; Müller, F.A.; Gräf, S. Large-Area Fabrication of Laser-Induced Periodic Surface Structures on Fused Silica Using Thin Gold Layers. Nanomaterials 2020, 10, 1187. https://doi.org/10.3390/nano10061187
Kunz C, Engel S, Müller FA, Gräf S. Large-Area Fabrication of Laser-Induced Periodic Surface Structures on Fused Silica Using Thin Gold Layers. Nanomaterials. 2020; 10(6):1187. https://doi.org/10.3390/nano10061187
Chicago/Turabian StyleKunz, Clemens, Sebastian Engel, Frank A. Müller, and Stephan Gräf. 2020. "Large-Area Fabrication of Laser-Induced Periodic Surface Structures on Fused Silica Using Thin Gold Layers" Nanomaterials 10, no. 6: 1187. https://doi.org/10.3390/nano10061187
APA StyleKunz, C., Engel, S., Müller, F. A., & Gräf, S. (2020). Large-Area Fabrication of Laser-Induced Periodic Surface Structures on Fused Silica Using Thin Gold Layers. Nanomaterials, 10(6), 1187. https://doi.org/10.3390/nano10061187