Organic Functionalized Graphene Oxide Behavior in Water
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Synthesis of Graphene Oxide (GO)
2.3. Functionalization of GO
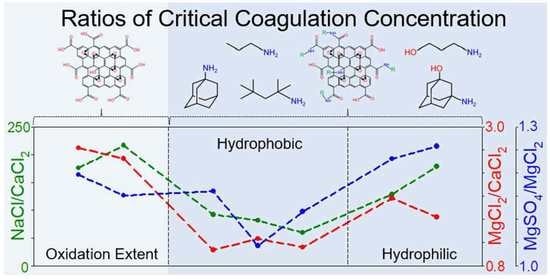
2.4. Critical Coagulation Concentration (CCC)
2.5. Hydrodynamic Diameter and Zeta Potential
2.6. Fourier Transform Infrared Spectroscopy (FTIR)
2.7. X-Ray Photoelectron Spectroscopy (XPS)
2.8. X-Ray Diffraction (XRD)
3. Theory
3.1. The Plate–Plate Geometry DLVO Interactions
3.2. Schulze–Hardy Rule (CCC Relationship for Sphere–Sphere Interaction)
3.3. CCC Relationship for Plate–Plate Interaction
4. Results and Discussion
4.1. Synthesis and Characterization of GO Materials
4.2. Effect of Oxidation Extent on Colloidal Stability of GO
4.3. Effect of Organic Coating on Colloidal Stability of GO
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nair, R.; Wu, H.; Jayaram, P.; Grigorieva, I.; Geim, A. Unimpeded permeation of water through helium-leak–tight graphene-based membranes. Science 2012, 335, 442–444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dreyer, D.R.; Park, S.; Bielawski, C.W.; Ruoff, R.S. The chemistry of graphene oxide. Chem. Soc. Rev. 2010, 39, 228–240. [Google Scholar] [CrossRef]
- Loh, K.P.; Bao, Q.; Eda, G.; Chhowalla, M. Graphene oxide as a chemically tunable platform for optical applications. Nat. Chem. 2010, 2, 1015. [Google Scholar] [CrossRef] [PubMed]
- Gudarzi, M.M. Colloidal stability of graphene oxide: Aggregation in two dimensions. Langmuir 2016, 32, 5058–5068. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, L.; Liu, L.; Gao, B.; Muñoz-Carpena, R.; Zhang, M.; Chen, H.; Zhou, Z.; Wang, H. Aggregation kinetics of graphene oxides in aqueous solutions: Experiments, mechanisms, and modeling. Langmuir 2013, 29, 15174–15181. [Google Scholar] [CrossRef]
- Ren, X.; Li, J.; Chen, C.; Gao, Y.; Chen, D.; Su, M.; Alsaedi, A.; Hayat, T. Graphene analogues in aquatic environments and porous media: Dispersion, aggregation, deposition and transformation. Environ. Sci. Nano 2018, 5, 1298–1340. [Google Scholar] [CrossRef]
- Wang, M.; Gao, B.; Tang, D.; Yu, C. Concurrent aggregation and transport of graphene oxide in saturated porous media: Roles of temperature, cation type, and electrolyte concentration. Environ. Pollut. 2018, 235, 350–357. [Google Scholar] [CrossRef]
- Chowdhury, I.; Mansukhani, N.D.; Guiney, L.M.; Hersam, M.C.; Bouchard, D. Aggregation and stability of reduced graphene oxide: Complex roles of divalent cations, pH, and natural organic matter. Environ. Sci. Technol. 2015, 49, 10886–10893. [Google Scholar] [CrossRef]
- Jiang, Y.; Raliya, R.; Liao, P.; Biswas, P.; Fortner, J.D. Graphene oxides in water: Assessing stability as a function of material and natural organic matter properties. Environ. Sci. Nano 2017, 4, 1484–1493. [Google Scholar] [CrossRef]
- Orth, E.S.; Ferreira, J.G.; Fonsaca, J.E.; Blaskievicz, S.F.; Domingues, S.H.; Dasgupta, A.; Terrones, M.; Zarbin, A.J. PKa determination of graphene-like materials: Validating chemical functionalization. J. Colloid Interface Sci. 2016, 467, 239–244. [Google Scholar] [CrossRef]
- Kashyap, S.; Mishra, S.; Behera, S.K. Aqueous colloidal stability of graphene oxide and chemically converted graphene. J. Nanopart. 2014, 2014, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kan, C.-C.; Genuino, D.A.D.; Rivera, K.K.P.; De Luna, M.D.G. Ultrasonic cleaning of polytetrafluoroethylene membrane fouled by natural organic matter. J. Membr. Sci. 2016, 497, 450–457. [Google Scholar] [CrossRef]
- Fraga, T.J.; Carvalho, M.N.; Ghislandi, M.G.; Motta Sobrinho, M.A.D. Functionalized graphene-based materials as innovative adsorbents of organic pollutants: A concise overview. Braz. J. Chem. Eng. 2019, 36, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Elimelech, M.; Gregory, J.; Jia, X. Particle Deposition and Aggregation: Measurement, Modelling and Simulation; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Chen, K.L.; Elimelech, M. Influence of humic acid on the aggregation kinetics of fullerene (C60) nanoparticles in monovalent and divalent electrolyte solutions. J. Colloid Interface Sci. 2007, 309, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.L.; Elimelech, M. Aggregation and deposition kinetics of fullerene (C60) nanoparticles. Langmuir 2006, 22, 10994–11001. [Google Scholar] [CrossRef]
- Trefalt, G. Derivation of the inverse Schulze-Hardy rule. Phys. Rev. E 2016, 93, 032612. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, I.; Duch, M.C.; Mansukhani, N.D.; Hersam, M.C.; Bouchard, D. Colloidal properties and stability of graphene oxide nanomaterials in the aquatic environment. Environ. Sci. Technol. 2013, 47, 6288–6296. [Google Scholar] [CrossRef]
- Chowdhury, I.; Duch, M.C.; Mansukhani, N.D.; Hersam, M.C.; Bouchard, D. Interactions of graphene oxide nanomaterials with natural organic matter and metal oxide surfaces. Environ. Sci. Technol. 2014, 48, 9382–9390. [Google Scholar] [CrossRef]
- Yang, K.; Chen, B.; Zhu, X.; Xing, B. Aggregation, adsorption, and morphological transformation of graphene oxide in aqueous solutions containing different metal cations. Environ. Sci. Technol. 2016, 50, 11066–11075. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.-J.; Xia, Q.-Q.; Zhang, Z.-H.; Zhao, L.; Zhang, G.-D.; Gao, J.-F.; Tang, L.-C. Simultaneous improvements in fire resistance and alarm response of GO paper via one-step 3-mercaptopropyltrimethoxysilane functionalization for efficient fire safety and prevention. Compos. Part A Appl. Sci. Manuf. 2020, 131, 105797. [Google Scholar] [CrossRef]
- Lian, Q.; Ahmad, Z.U.; Gang, D.D.; Zappi, M.E.; Fortela, D.L.B.; Hernandez, R. The effects of carbon disulfide driven functionalization on graphene oxide for enhanced Pb (II) adsorption: Investigation of adsorption mechanism. Chemosphere 2020, 248, 126078. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.; An, S.; Lee, J.; Zeng, Q.; Fortner, J.D. Engineering Graphene Oxide Laminate Membranes for Enhanced Flux and Boron Treatment with Polyethylenimine (PEI) Polymers. ACS Appl. Mater. Interfaces 2018, 11, 924–929. [Google Scholar] [CrossRef] [PubMed]
- Hotze, E.M.; Phenrat, T.; Lowry, G.V. Nanoparticle aggregation: Challenges to understanding transport and reactivity in the environment. J. Environ. Qual. 2010, 39, 1909–1924. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ortega-Vinuesa, J.; Martın-Rodrıguez, A.; Hidalgo-Alvarez, R. Colloidal stability of polymer colloids with different interfacial properties: Mechanisms. J. Colloid Interface Sci. 1996, 184, 259–267. [Google Scholar] [CrossRef]
- Shahriary, L.; Athawale, A.A. Graphene oxide synthesized by using modified hummers approach. Int. J. Renew. Energy Environ. Eng. 2014, 2, 58–63. [Google Scholar]
- Humers, W.; Offeman, R. Preparation of graphitic oxide. J. Am. Chem. Soc. 1958, 80, 1339. [Google Scholar] [CrossRef]
- Mylon, S.E.; Chen, K.L.; Elimelech, M. Influence of natural organic matter and ionic composition on the kinetics and structure of hematite colloid aggregation: Implications to iron depletion in estuaries. Langmuir 2004, 20, 9000–9006. [Google Scholar] [CrossRef]
- Holthoff, H.; Egelhaaf, S.U.; Borkovec, M.; Schurtenberger, P.; Sticher, H. Coagulation rate measurements of colloidal particles by simultaneous static and dynamic light scattering. Langmuir 1996, 12, 5541–5549. [Google Scholar] [CrossRef]
- Chen, K.L.; Mylon, S.E.; Elimelech, M. Aggregation kinetics of alginate-coated hematite nanoparticles in monovalent and divalent electrolytes. Environ. Sci. Technol. 2006, 40, 1516–1523. [Google Scholar] [CrossRef] [PubMed]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Parsegian, V.A. Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Gudarzi, M.M.; Moghadam, M.H.M.; Sharif, F. Spontaneous exfoliation of graphite oxide in polar aprotic solvents as the route to produce graphene oxide–organic solvents liquid crystals. Carbon 2013, 64, 403–415. [Google Scholar] [CrossRef]
- Casero, E.; Alonso, C.; Petit-Domínguez, M.D.; Vázquez, L.; Parra-Alfambra, A.M.; Merino, P.; Álvarez-García, S.; De Andrés, A.; Suárez, E.; Pariente, F. Lactate biosensor based on a bionanocomposite composed of titanium oxide nanoparticles, photocatalytically reduced graphene, and lactate oxidase. Microchim. Acta 2014, 181, 79–87. [Google Scholar] [CrossRef] [Green Version]
- Silverstein, R.M.; Bassler, G.C. Spectrometric identification of organic compounds. J. Chem. Educ. 1962, 39, 546. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Z.; Zhao, Q.; Huang, J.; Shen, H.; Zhang, Z. Enhanced chemotherapy efficacy by sequential delivery of siRNA and anticancer drugs using PEI-grafted graphene oxide. Small 2011, 7, 460–464. [Google Scholar] [CrossRef] [PubMed]
- Hung, W.-S.; Tsou, C.-H.; De Guzman, M.; An, Q.-F.; Liu, Y.-L.; Zhang, Y.-M.; Hu, C.-C.; Lee, K.-R.; Lai, J.-Y. Cross-linking with diamine monomers to prepare composite graphene oxide-framework membranes with varying d-spacing. Chem. Mater. 2014, 26, 2983–2990. [Google Scholar] [CrossRef]
- Lotya, M.; Rakovich, A.; Donegan, J.F.; Coleman, J.N. Measuring the lateral size of liquid-exfoliated nanosheets with dynamic light scattering. Nanotechnology 2013, 24, 265703. [Google Scholar] [CrossRef]
- Jiang, Y.; Raliya, R.; Fortner, J.D.; Biswas, P. Graphene oxides in water: Correlating morphology and surface chemistry with aggregation behavior. Environ. Sci. Technol. 2016, 50, 6964–6973. [Google Scholar] [CrossRef]
- Yi, P.; Chen, K.L. Influence of surface oxidation on the aggregation and deposition kinetics of multiwalled carbon nanotubes in monovalent and divalent electrolytes. Langmuir 2011, 27, 3588–3599. [Google Scholar] [CrossRef]
- Huynh, K.A.; Chen, K.L. Aggregation kinetics of citrate and polyvinylpyrrolidone coated silver nanoparticles in monovalent and divalent electrolyte solutions. Environ. Sci. Technol. 2011, 45, 5564–5571. [Google Scholar] [CrossRef] [Green Version]
- Cao, T.; Szilagyi, I.; Oncsik, T.; Borkovec, M.; Trefalt, G. Aggregation of colloidal particles in the presence of multivalent co-ions: The inverse Schulze–Hardy rule. Langmuir 2015, 31, 6610–6614. [Google Scholar] [CrossRef]
- Ruiz-Cabello, F.J.M.; Moazzami-Gudarzi, M.; Elzbieciak-Wodka, M.; Maroni, P.; Labbez, C.; Borkovec, M.; Trefalt, G. Long-ranged and soft interactions between charged colloidal particles induced by multivalent coions. Soft Matter 2015, 11, 1562–1571. [Google Scholar] [CrossRef] [Green Version]
- Moroi, Y. Stability of Colloidal Particles. In Micelles; Springer: Berlin/Heidelberg, Germany, 1992; pp. 131–148. [Google Scholar]
- De Carvalho, S.J.; Fenley, M.O.; Da Silva, F.L.s.B. Protein−Ion Binding Process on Finite Macromolecular Concentration. A Poisson−Boltzmann and Monte Carlo Study. J. Phys. Chem. B 2008, 112, 16766–16776. [Google Scholar] [CrossRef] [PubMed]
- Das, P.K.; Bhattacharjee, S.; Moussa, W. Electrostatic double layer force between two spherical particles in a straight cylindrical capillary: Finite element analysis. Langmuir 2003, 19, 4162–4172. [Google Scholar] [CrossRef]
- Park, S.; Lee, K.-S.; Bozoklu, G.; Cai, W.; Nguyen, S.T.; Ruoff, R.S. Graphene oxide papers modified by divalent ions—Enhancing mechanical properties via chemical cross-linking. ACS Nano 2008, 2, 572–578. [Google Scholar] [CrossRef] [PubMed]






| Sample | O-C=O (%) | C=O (%) | C-O-C (%) | C-O/C-N (%) | C-C (%) |
|---|---|---|---|---|---|
| Graphene oxide (GO) | 0.55 | 6.62 | 36.53 | 10.89 | 45.42 |
| Highly oxidized GO (HGO) | 0.07 | 4.54 | 52.73 | 0.92 | 41.75 |
| Propylamine GO | 1.86 | 9.23 | 16.41 | 28.40 | 44.10 |
| Tert-octylamine GO | 1.38 | 5.56 | 11.15 | 30.65 | 51.27 |
| 1-adamantylamine GO | 0.35 | 7.49 | 7.84 | 29.93 | 54.50 |
| 3-amino-1-propanol GO | 0.00 | 3.40 | 12.41 | 16.45 | 67.74 |
| 3-amino-1-adamantanol GO | 0.00 | 4.06 | 10.68 | 16.88 | 68.38 |
| Samples | NaCl (mM) | CaCl2 (mM) | MgCl2 (mM) | MgSO4 (mM) | CCC Ratio | ||||
|---|---|---|---|---|---|---|---|---|---|
| NaCl/ CaCl2 | NaCl/ MgCl2 | NaCl/ MgSO4 | MgCl2/ CaCl2 | MgSO4/ MgCl2 | |||||
| GO | 246.38 | 1.40 | 3.97 | 4.75 | 27.46 | 25.96 | 25.70 | 2.84 | 1.20 |
| HGO | 387.18 | 1.79 | 4.75 | 5.47 | 27.76 | 26.45 | 26.15 | 2.65 | 1.15 |
| Propylamine GO | 101.38 | 1.10 | 1.18 | 1.37 | 26.42 | 26.43 | 26.21 | 1.07 | 1.16 |
| Tert-octylamine GO | 104.55 | 1.28 | 1.62 | 1.69 | 26.46 | 26.01 | 25.95 | 1.27 | 1.04 |
| 1-adamantylamine GO | 118.29 | 1.99 | 2.23 | 2.49 | 25.90 | 25.73 | 25.57 | 1.12 | 1.12 |
| 3-amino-1-propanol GO | 153.05 | 1.19 | 2.34 | 2.88 | 27.01 | 26.03 | 25.73 | 1.97 | 1.23 |
| 3-amino-1-adamantanol GO | 303.31 | 1.70 | 2.79 | 3.51 | 27.48 | 26.76 | 26.43 | 1.64 | 1.26 |
| Schulze-Hardy Rule | 22–26 | 1 | |||||||
| Plate-Plate Interaction | 22 | 1 | |||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Lee, J.; Wang, W.; Fortner, J. Organic Functionalized Graphene Oxide Behavior in Water. Nanomaterials 2020, 10, 1228. https://doi.org/10.3390/nano10061228
Kim C, Lee J, Wang W, Fortner J. Organic Functionalized Graphene Oxide Behavior in Water. Nanomaterials. 2020; 10(6):1228. https://doi.org/10.3390/nano10061228
Chicago/Turabian StyleKim, Changwoo, Junseok Lee, Will Wang, and John Fortner. 2020. "Organic Functionalized Graphene Oxide Behavior in Water" Nanomaterials 10, no. 6: 1228. https://doi.org/10.3390/nano10061228
APA StyleKim, C., Lee, J., Wang, W., & Fortner, J. (2020). Organic Functionalized Graphene Oxide Behavior in Water. Nanomaterials, 10(6), 1228. https://doi.org/10.3390/nano10061228