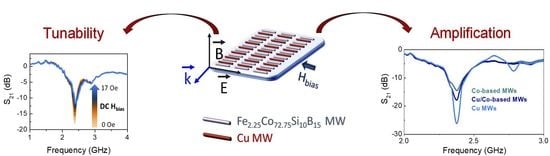
Boosting the Tunable Microwave Scattering Signature of Sensing Array Platforms Consisting of Amorphous Ferromagnetic Fe2.25Co72.75Si10B15 Microwires and Its Amplification by Intercalating Cu Microwires
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication and Characterization of the Co-Based Amorphous Ferromagnetic MWs
2.2. Design of the Sensing Platforms Composed of Co-Based and Co-Based + Cu MWs Linear Arrays
- Configuration 1: one sensing platform composed by a 15 MWs linear array. The MWs have a length of 4 cm and they are equidistantly separated by 0.5 cm.
- Configuration 2: one sensing platform composed by three columns of 15 MWs linear array. The MWs have a length of 4 cm, and they are separated equidistantly by 0.5 cm. The spacing between columns is also set to 0.5 cm.
- Configuration 3: two sensing platforms of the configuration 2 in a tandem form.
2.3. Operational Physical Basis and High-Frequency Characterization
3. Results and Discussion
3.1. Structural and Magnetic Characterization of Co-Based MWs
3.2. Evolution of the Microwave Scattering Properties in Co-Based MWs Linear Arrays
3.3. Microwave Scattering Experiments Performed in Co-Based MWs Sensing Array Platforms by Applying DC/AC Magnetic Fields
3.4. Microwave Scattering Experiments Performed in Cu and Co-Based MWs Sensing Array Platforms by Applying DC Magnetic Fields
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McHenry, M.E.; Willard, M.E.; Laughlin, D.E. Amorphous and nanocrystalline materials for applications as soft magnets. Prog. Mater. Sci. 1999, 44, 291–433. [Google Scholar] [CrossRef]
- Qin, F.; Peng, H.-X. Ferromagnetic microwires enabled multifunctional composite materials. Prog. Mater. Sci. 2013, 58, 183–259. [Google Scholar] [CrossRef]
- Vázquez, M. Magnetic Nano and Microwires; Woodhead Publishing: Sawston, UK, 2015. [Google Scholar]
- Huang, L.; Duan, Y.; Liu, J.; Zeng, Y.; Ma, G.; Pang, H.; Zhang, W. Bionic composite metamaterials for harvesting of microwave and integration of multifunctionality. Compos. Sci. Technol. 2021, 204, 108640. [Google Scholar] [CrossRef]
- Estevez, D.; Qin, F.; Luo, Y.; Quan, L.; Mai, Y.-W.; Panina, L.; Peng, H.-X. Tunable negative permittivity in nano-carbon coated magnetic microwire polymer metacomposites. Compos. Sci. Technol. 2019, 171, 206–217. [Google Scholar] [CrossRef]
- Zheng, X.; Qin, F.; Wang, H.; Mai, Y.-W.; Peng, H. Microwave absorbing properties of composites containing ultra-low loading of optimized microwires. Compos. Sci. Technol. 2017, 151, 62–70. [Google Scholar] [CrossRef]
- Xu, Y.; Uddin, A.; Estevez, D.; Luo, Y.; Peng, H.; Qin, F. Lightweight microwire/graphene/silicone rubber composites for efficient electromagnetic interference shielding and low microwave reflectivity. Compos. Sci. Technol. 2020, 189, 108022. [Google Scholar] [CrossRef]
- Dijvejin, Z.A.; Kazemi, K.K.; Zarasvand, K.A.; Zarifi, M.H.; Golovin, K. Kirigami enabled microwave resonator arrays for wireless, flexible, passive strain sensing. ACS Appl. Mater. Interfaces 2020, 12, 44256–44264. [Google Scholar] [CrossRef]
- Vijayakumar, K.; Wylie, S.R.; Cullen, J.D.; Wright, C.C.; Ai-Shamma’A, A.I. Non invasive rail track detection system using microwave sensor. J. Phys. Conf. Ser. 2009, 178, 012033. [Google Scholar] [CrossRef]
- Yuan, B.; Yu, L.; Sheng, L.; An, K.; Zhao, X. Comparison of electromagnetic interference shielding properties between single-wall carbon nanotube and graphene sheet/polyaniline composites. J. Phys. D Appl. Phys. 2012, 45, 235108. [Google Scholar] [CrossRef]
- Qin, F.; Peng, H.X.; Pankratov, N.; Phan, M.H.; Panina, L.V.; Ipatov, M.; Zhukova, V.; Zhukov, A.; González, J. Exceptional electromagnetic interference shielding properties of ferromagnetic microwires enabled polymer composites. J. Appl. Phys. 2010, 108, 044510. [Google Scholar] [CrossRef] [Green Version]
- Zeng, X.; Jiang, G.; Zhu, L.; Wang, C.; Chen, M.; Yu, R. Fe3O4 Nanoflower-carbon nanotube composites for microwave shielding. ACS Appl. Nano Mater. 2019, 2, 5475–5482. [Google Scholar] [CrossRef]
- Gund, G.S.; Jung, M.G.; Shin, K.-Y.; Park, H.S. Two-dimensional metallic niobium diselenide for sub-micrometer-thin antennas in wireless communication systems. ACS Nano 2019, 13, 14114–14121. [Google Scholar] [CrossRef] [PubMed]
- Herrero-Gómez, C.; Aragón, A.M.; Hernando-Rydings, M.; Marín, P.; Hernando, A. Stress and field contactless sensor based on the scattering of electromagnetic waves by a single ferromagnetic microwire. Appl. Phys. Lett. 2014, 105, 092405. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.; Pang, L.-X.; Wang, D.-W.; Qi, Z.-M.; Reaney, I.M. High quality factor, ultralow sintering temperature Li6B4O9 microwave dielectric ceramics with ultralow density for antenna substrates. ACS Sustain. Chem. Eng. 2018, 6, 11138–11143. [Google Scholar] [CrossRef] [Green Version]
- Kraus, L.; Infante, G.; Frait, Z.; Vázquez, M. Ferromagnetic resonance in microwires and nanowires. Phys. Rev. B 2011, 83, 174438. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.; Kiourti, A.; Wang, H.; Zhao, S.; Zhao, G.; Lu, X.; Volakis, J.L.; He, X. Enhanced microwave hyperthermia of cancer cells with fullerene. Mol. Pharm. 2016, 13, 2184–2192. [Google Scholar] [CrossRef] [PubMed]
- Kurlyandskaya, G.; Sánchez, M.L.; Hernando, B.; Prida, V.M.; Gorria, P.; Tejedor, M. Giant-magnetoimpedance-based sensitive element as a model for biosensors. Appl. Phys. Lett. 2003, 82, 3053. [Google Scholar] [CrossRef]
- Marín, P.; Marcos, M.; Hernando, A. High magnetomechanical coupling on magnetic microwire for sensors with biological applications. Appl. Phys. Lett. 2010, 96, 262512. [Google Scholar] [CrossRef] [Green Version]
- Gas, P.; Miaskowski, A.; Subramanian, M. In silico study on tumor-size-dependent thermal profiles inside an anthropomorphic female breast phantom subjected to multi-dipole antenna array. Int. J. Mol. Sci. 2020, 21, 8597. [Google Scholar] [CrossRef]
- Liu, W.; Miroshnichenko, A.E.; Neshev, D.N.; Kivshar, Y.S. Broadband unidirectional scattering by magneto-electric core–shell nanoparticles. ACS Nano 2012, 6, 5489–5497. [Google Scholar] [CrossRef]
- Vázquez, M.; Knobel, M.; Sánchez, M.L.; Valenzuela, R.; Zhukov, A. Giant magnetoimpedance effect in soft magnetic wires for sensor applications. Sens. Actuators A Phys. 1997, 59, 20–29. [Google Scholar] [CrossRef]
- García-Prieto, M.; Pina, E.; Zhukov, A.; Larin, V.; Marín, P.; Vázquez, M.; Hernando, A. Glass-coated Co-rich amorphous microwires with enhanced permeability. Sens. Actuators A Phys. 2000, 81, 227–231. [Google Scholar] [CrossRef]
- Larin, V.; Torcunov, A.; Zhukov, A.; González, J.; Vázquez, M.; Panina, L. Preparation and properties of glass-coated microwires. J. Magn. Magn. Mater. 2002, 249, 39–45. [Google Scholar] [CrossRef]
- Vázquez, M.; Zhukov, A. Magnetic properties of glass-coated amorphous and nanocrystalline microwires. J. Magn. Magn. Mater. 1996, 160, 223–228. [Google Scholar] [CrossRef]
- Taylor, G.F. A Method of Drawing Metallic Filaments and a Discussion of their Properties and Uses. Phys. Rev. 1924, 23, 655–660. [Google Scholar] [CrossRef]
- Chiriac, H.; Ovari, T.; Pop, G.; Barariu, F. Amorphous glass-covered magnetic wires for sensing applications. Sens. Actuators A Phys. 1997, 59, 243–251. [Google Scholar] [CrossRef]
- Usov, N.; Antonov, A.; Lagar’Kov, A. Theory of giant magneto-impedance effect in amorphous wires with different types of magnetic anisotropy. J. Magn. Magn. Mater. 1998, 185, 159–173. [Google Scholar] [CrossRef]
- Peng, H.; Qin, F.; Phan, M.; Tang, J.; Panina, L.; Ipatov, M.; Zhukova, V.; Zhukov, A.; González, J. Co-based magnetic microwire and field-tunable multifunctional macro-composites. J. Non-Cryst. Solids 2009, 355, 1380–1386. [Google Scholar] [CrossRef]
- González-Alonso, D.; González-Legarreta, L.; Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Zhukov, A. Magnetoimpedance response and field sensitivity in stress-annealed Co-based microwires for sensor applications. Sensors 2020, 20, 3227. [Google Scholar] [CrossRef] [PubMed]
- González-Legarreta, L.; Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Route of magnetoimpedance and domain walls dynamics optimization in Co-based microwires. J. Alloys Compd. 2020, 830, 154576. [Google Scholar] [CrossRef]
- Corodeanu, S.; Chiriac, H.; Damian, A.; Lupu, N.; Óvári, T.-A. Field and current controlled domain wall propagation in twisted glass-coated magnetic microwires. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Panina, L.V.; Ipatov, M.; Zhukova, V.; Zhukov, A.; González, J. Magnetic field effects in artificial dielectrics with arrays of magnetic wires at microwaves. J. Appl. Phys. 2011, 109, 053901. [Google Scholar] [CrossRef]
- Reynet, O.; Adenot, A.-L.; Deprot, S.; Acher, O.; Latrach, M. Effect of the magnetic properties of the inclusions on the high-frequency dielectric response of diluted composites. Phys. Rev. B 2002, 66, 094412. [Google Scholar] [CrossRef] [Green Version]
- Uddin, A.; Qin, F.; Estevez, D.; Jiang, S.; Panina, L.; Peng, H. Microwave programmable response of Co-based microwire polymer composites through wire microstructure and arrangement optimization. Compos. Part B Eng. 2019, 176, 107190. [Google Scholar] [CrossRef] [Green Version]
- Hernando, A.; López-Domínguez, V.; Ricciardi, E.; Osiak, K.; Marín, P.; Riccardi, E. Tuned scattering of electromagnetic waves by a finite length ferromagnetic microwire. IEEE Trans. Antennas Propag. 2015, 64, 1112–1115. [Google Scholar] [CrossRef]
- Gueye, P.G.B.; López-Sánchez, J.; Navarro, E.; Serrano, A.; Marín, P. Control of the length of Fe73.5Si13.5Nb3Cu1B9 microwires to be used for magnetic and microwave absorbing purposes. ACS Appl. Mater. Interfaces 2020, 12, 15644–15656. [Google Scholar] [CrossRef]
- Panina, L.V.; Sandacci, S.I.; Makhnovskiy, D.P. Stress effect on magnetoimpedance in amorphous wires at gigahertz frequencies and application to stress-tunable microwave composite materials. J. Appl. Phys. 2005, 97, 013701. [Google Scholar] [CrossRef] [Green Version]
- Ipatov, M.; Zhukova, V.; Zhukov, A.; Gonzalez, J.; Zvezdin, A. Low-field hysteresis in the magnetoimpedance of amorphous microwires. Phys. Rev. B 2010, 81, 134421. [Google Scholar] [CrossRef]
- Gorriti, A.; Marín, P.; Cortina, D.; Hernando, A. Microwave attenuation with composite of copper microwires. J. Magn. Magn. Mater. 2010, 322, 1505–1510. [Google Scholar] [CrossRef]
- Landy, N.; Smith, D.R. A full-parameter unidirectional metamaterial cloak for microwaves. Nat. Mater. 2012, 12, 25–28. [Google Scholar] [CrossRef]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- López-Domínguez, V.; García, M.A.; Marín, P.; Hernando, A. Tuning metamaterials by using amorphous magnetic microwires. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, L.; Zhao, Q.; Zhao, H.; Zhou, J. Ferrite-based magnetically tunable left-handed metamaterial composed of SRRs and wires. Opt. Express 2008, 16, 17269–17275. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zhou, J.; Zhao, Q.; Li, B.; Kang, L.; Bai, Y. Magnetotunable left-handed material consisting of yttrium iron garnet slab and metallic wires. Appl. Phys. Lett. 2007, 91, 131107. [Google Scholar] [CrossRef]
- Carbonell, J.; García-Miquel, H.; Sánchez-Dehesa, J. Double negative metamaterials based on ferromagnetic microwires. Phys. Rev. B 2010, 81, 024401. [Google Scholar] [CrossRef]
- Marín, P. Wireless stress sensor based on magnetic microwires. In Magnetic Sensors—Development Trends and Applications Parameters; Asfour, A., Ed.; IntechOpen: London, UK, 2017; pp. 17–29. [Google Scholar]
- Archilla, D.; Moya, A.; Hernando, A.; Marín, P. Optimization of tunable GHz micro-antennas based on giant magnetoimpedance. J. Magn. Magn. Mater. 2019, 469, 289–295. [Google Scholar] [CrossRef]
- Makhnovskiy, D.P.; Panina, L.V.; Mapps, D.J. Field-dependent surface impedance tensor in amorphous wires with two types of magnetic anisotropy: Helical and circumferential. Phys. Rev. B 2001, 63, 144424. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Qin, F.; Xing, D.; Cao, F.; Wang, X.; Peng, H.; Sun, J. Relating residual stress and microstructure to mechanical and giant magneto-impedance properties in cold-drawn Co-based amorphous microwires. Acta Mater. 2012, 60, 5425–5436. [Google Scholar] [CrossRef]
- Moya, A.; Archilla, D.; Navarro, E.; Hernando, A.; Marín, P. Scattering of microwaves by a passive array antenna based on amorphous ferromagnetic microwires for wireless sensors with biomedical applications. Sensors 2019, 19, 3060. [Google Scholar] [CrossRef] [Green Version]
- Brookner, E. Practical Phased Array Antenna Systems; Artech House: Boston, MA, USA, 1991. [Google Scholar]
- Panina, L.V.; Makhnovskiy, D.P.; Beklemisheva, A.V.; Salem, M.; Yudanov, N.A. Functional magnetoelectric composites with magnetostrictive microwires. SN Appl. Sci. 2019, 1, 249. [Google Scholar] [CrossRef] [Green Version]
- Qin, F.; Peng, H.-X.; Tang, J.; Qin, L.-C. Ferromagnetic microwires enabled polymer composites for sensing applications. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1823–1828. [Google Scholar] [CrossRef]
- Duan, Y.; Xiao, Z.; Yan, X.; Gao, Z.; Tang, Y.; Hou, L.; Li, Q.; Ning, G.; Li, Y. Enhanced electromagnetic microwave absorption property of peapod-like MnO@carbon nanowires. ACS Appl. Mater. Interfaces 2018, 10, 40078–40087. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.-H.; Tao, R.; Luo, P.; Shu, X.; Ban, G.-D. Preparation and microwave absorbing property of carbon fiber/polyurethane radar absorbing coating. RSC Adv. 2017, 7, 46060–46068. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Huang, D.; Yang, Y.; Kang, F.; Gu, J. Fe3O4/carbon composite nanofiber absorber with enhanced microwave a sorption performance. Mater. Sci. Eng. B 2013, 178, 1–9. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Archilla, D.; López-Sánchez, J.; Hernando, A.; Navarro, E.; Marín, P. Boosting the Tunable Microwave Scattering Signature of Sensing Array Platforms Consisting of Amorphous Ferromagnetic Fe2.25Co72.75Si10B15 Microwires and Its Amplification by Intercalating Cu Microwires. Nanomaterials 2021, 11, 920. https://doi.org/10.3390/nano11040920
Archilla D, López-Sánchez J, Hernando A, Navarro E, Marín P. Boosting the Tunable Microwave Scattering Signature of Sensing Array Platforms Consisting of Amorphous Ferromagnetic Fe2.25Co72.75Si10B15 Microwires and Its Amplification by Intercalating Cu Microwires. Nanomaterials. 2021; 11(4):920. https://doi.org/10.3390/nano11040920
Chicago/Turabian StyleArchilla, Diego, Jesús López-Sánchez, Antonio Hernando, Elena Navarro, and Pilar Marín. 2021. "Boosting the Tunable Microwave Scattering Signature of Sensing Array Platforms Consisting of Amorphous Ferromagnetic Fe2.25Co72.75Si10B15 Microwires and Its Amplification by Intercalating Cu Microwires" Nanomaterials 11, no. 4: 920. https://doi.org/10.3390/nano11040920
APA StyleArchilla, D., López-Sánchez, J., Hernando, A., Navarro, E., & Marín, P. (2021). Boosting the Tunable Microwave Scattering Signature of Sensing Array Platforms Consisting of Amorphous Ferromagnetic Fe2.25Co72.75Si10B15 Microwires and Its Amplification by Intercalating Cu Microwires. Nanomaterials, 11(4), 920. https://doi.org/10.3390/nano11040920