Highly Sensitive Plasmonic Structures Utilizing a Silicon Dioxide Overlayer
Abstract
:1. Introduction
2. Theoretical Background
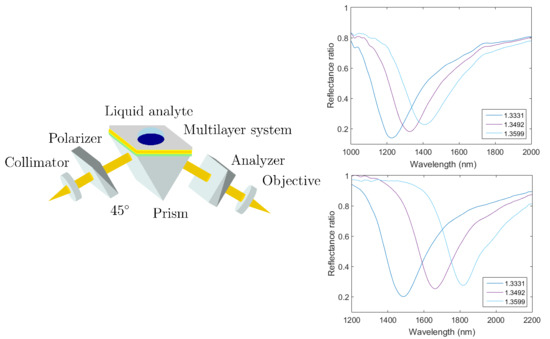
2.1. Structure Design
2.2. Transfer Matrix Method
2.3. Material Parameters
2.3.1. Substrate (BK7 Glass) and Silicon Dioxide ()
2.3.2. Gold Layer
2.3.3. Adhesion Chromium Layers
3. Theoretical Analysis
4. Fabrication of Structures
5. Responses of Real Structures
6. Experimental Analysis
Experimental Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kretschmann, E.; Raether, H. Radiative decay of nonradiative surface plasmons excited by light. Z. Naturforschung A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer: New York, NY, USA, 1988. [Google Scholar]
- Homola, J.; Yee, S.; Gauglitz, G. Surface plasmon resonance sensors: Review. Sens. Actuators B Chem. 1999, 54, 3–15. [Google Scholar] [CrossRef]
- Homola, J. Surface Plasmon Resonance Based Sensors; Springer: New York, NY, USA, 2006. [Google Scholar]
- Manuel, M.; Vidal, B.; Lopéz, R.; Alegret, S.; Alonso-Chamarro, J.; Garces, I.; Mateo, J. Determination of probable alcohol yield in musts by means of an SPR optical sensor. Sens. Actuators B Chem. 1993, 11, 455–459. [Google Scholar] [CrossRef]
- Liedberg, B.; Nylander, C.; Lundström, I. Principles of biosensing with an extended coupling matrix and surface plasmon resonance. Sens. Actuators B Chem. 1993, 11, 63–72. [Google Scholar] [CrossRef]
- Dostálek, J.; Vaisocherova, H.; Homola, J. Multichannel surface plasmon resonance biosensor with wavelength division multiplexing. Sens. Actuators B Chem. 2005, 108, 758–764. [Google Scholar] [CrossRef]
- Gwon, H.R.; Lee, S.H. Spectral and angular responses of surface plasmon resonance based on the Kretschmann prism configuration. Mater. Trans. 2010, 51, 1150–1155. [Google Scholar] [CrossRef]
- Shalabney, A.; Abdulhalim, I. Figure-of-merit enhancement of surface plasmon resonance sensors in the spectral interrogation. Opt. Lett. 2012, 37, 1175–1177. [Google Scholar] [CrossRef]
- Urbancova, P.; Chylek, J.; Hlubina, P.; Pudis, D. Guided-Mode Resonance-Based Relative Humidity Sensing Employing a Planar Waveguide Structure. Sensors 2020, 20, 6788. [Google Scholar] [CrossRef]
- Nikitin, P.; Beloglazov, A.; Kochergin, V.; Valeiko, M.; Ksenevich, T. Surface plasmon resonance interferometry for biological and chemical sensing. Sens. Actuators B Chem. 1999, 54, 43–50. [Google Scholar] [CrossRef]
- Hlubina, P.; Ciprian, D. Spectral phase shift of surface plasmon resonance in the Kretschmann configuration: Theory and experiment. Plasmonics 2017, 12, 1071–1078. [Google Scholar] [CrossRef]
- Lahav, A.; Shalabaney, A.; Abdulhalim, I. Surface plasmon sensor with enhanced sensitivity using top nano dielectric layer. J. Nanophotonics 2009, 3, 031501. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Dong, J.; Hu, S.; Zhu, W.; Qiu, W.; Lu, H.; Yu, J.; Guan, H.; Gao, S.; et al. Sensitivity-enhanced surface plasmon resonance sensor utilizing a tungsten disulfide (WS2) nanosheets overlayer. Photonics Res. 2018, 6, 485–491. [Google Scholar] [CrossRef]
- Maurya, J.B.; Prajapati, Y.K.; Singh, V.; Saini, J.P.; Tripathi, R. Performance of graphene–MoS2 based surface plasmon resonance sensor using Silicon layer. Opt. Quant. Electron. 2015, 47, 3599–3611. [Google Scholar] [CrossRef]
- Szunerits, S.; Shalabney, A.; Boukherroub, R.; Abdulhalim, I. Dielectric coated plasmonic interfaces: Their interest for sensitive sensing of analyte-ligand interactions. Rev. Anal. Chem. 2012, 31, 15–28. [Google Scholar] [CrossRef]
- Mishra, A.K.; Mishra, S.K.; Verma, R.K. An SPR-based sensor with an extremely large dynamic range of refractive index measurements in the visible region. J. Phys. D Appl. Phys. 2015, 48, 435502. [Google Scholar] [CrossRef]
- Sharma, A.K. Analyzing the application of silicon–silver–2D nanomaterial–Al2O3 heterojunction in plasmonic sensor and its performance evaluation. Opt. Commun. 2018, 410, 75–82. [Google Scholar] [CrossRef]
- Samdani, S.; Kala, A.; Kaurav, R.; Kaladharan, S.; Achanta, V.G. Reusable Biosensor Based on Differential Phase Detection at the Point of Darkness. Adv. Photonics Res. 2021, 2, 2000147. [Google Scholar] [CrossRef]
- Mahajna, S.; Neumann, M.; Eyal, O.; Shalabney, A. Plasmon-Waveguide Resonances with Enhanced Figure of Merit and Their Potential for Anisotropic Biosensing in the Near Infrared Region. J. Sens. 2016, 2016, 898315. [Google Scholar] [CrossRef]
- Nesterenko, D.V.; Hayashi, S.; Sekkat, Z. Extremely narrow resonances, giant sensitivity and field enhancement in low-loss waveguide sensors. J. Opt. 2016, 18, 065004. [Google Scholar] [CrossRef]
- Kabashin, A.; Evans, P.; Pastkovsky, S.; Hendren, W.; Wurtz, G.A.; Atkinson, R.; Pollard, R.; Podolskiy, V.A.; Zayats, A.V. Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 2009, 8, 867–871. [Google Scholar] [CrossRef]
- Cetin, A.E.; Etezadi, D.; Galarreta, B.C.; Busson, M.P.; Eksioglu, Y.; Altug, H. Plasmonic Nanohole Arrays on a Robust Hybrid Substrate for Highly Sensitive Label-Free Biosensing. ACS Photonics 2015, 2, 1167–1174. [Google Scholar] [CrossRef]
- Sreekanth, K.V.; Alapan, Y.; ElKabbash, M.; Ilkerand, E.; Hinczewski, M.; Gurkan, U.A.; Luca, A.D.; Strangi, G. Extreme sensitivity biosensing platform based on hyperbolic metamaterials. Nat. Mater. 2016, 15, 621–627. [Google Scholar] [CrossRef] [PubMed]
- Garoli, D.; Calandrini, E.; Giovannini, G.; Hubarevich, A.; Caligiuri, V.; Angelis, F.D. Nanoporous gold metamaterials for high sensitivity plasmonic sensing. Nanoscale Horiz. 2019, 4, 1153–1157. [Google Scholar] [CrossRef]
- Yan, R.; Wang, T.; Yue, X.; Wang, H.; Zhang, Y.H.; Xu, P.; Wang, L.; Wang, Y.; Zhang, J. Highly sensitive plasmonic nanorod hyperbolic metamaterial biosensor. Photonics Res. 2022, 10, 84–95. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Polyanskiy, M.N. Refractive Index Database. Available online: http://refractiveindex.info (accessed on 18 July 2022).
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Vial, A.; Grimault, A.S.; Macías, D.; Barchiesi, D.; Chapelle, M.L.D.L. Improved analytical fit of gold dispersion: Application to the modeling of extinction spectra with a finite-difference time-domain method. Phys. Rev. B 2005, 71, 085416. [Google Scholar] [CrossRef]
- Vial, A.; Laroche, T. Description of dispersion properties of metals by means of the critical points model and application to the study of resonant structures using the FDTD method. J. Phys. D Appl. Phys. 2007, 40, 7152–7158. [Google Scholar] [CrossRef]
- Yang, Z.; Gu, D.; Gao, Y. An improved dispersion law of thin metal film and application to the study of surface plasmon resonance phenomenon. Opt. Commun. 2014, 329, 180–183. [Google Scholar] [CrossRef]
- Sinibaldi, A.; Danz, N.; Descrovi, E.; Munzert, P.; Schulz, U.; Sonntag, F.; Dominici, L.; Michelotti, F. Direct comparison of the performance of Bloch surface wave and surface plasmon polariton sensors. Sens. Actuators B Chem. 2012, 174, 292–298. [Google Scholar] [CrossRef]
- Refki, S.; Hayashi, S.; Ishitobi, H.; Nesterenko, D.V.; Rahmouni, A.; Inouye, Y.; Sekkat, Z. Resolution Enhancement of Plasmonic Sensors by Metal-Insulator-Metal Structures. Ann. Der Phys. 2018, 530, 1700411. [Google Scholar] [CrossRef]
- Tikhonravov, A.V.; Trubetskov, M.K.; Hrdina, J.; Sobota, J. Characterization of quasi-rugate filters using ellipsometric measurements. Thin Solid Films 1996, 277, 83–89. [Google Scholar] [CrossRef]
- Chlebus, R.; Chylek, J.; Ciprian, D.; Hlubina, P. Surface plasmon resonance based measurement of the dielectric function of a thin metal film. Sensors 2018, 18, 3693. [Google Scholar] [CrossRef] [PubMed]
- Shrivastav, A.M.; Satish, L.; Kushmaro, A.; Shvalya, V.; Cvelbar, U.; Abdulhalim, I. Engineering the penetration depth of nearly guided wave surface plasmon resonance towards application in bacterial cells monitoring. Sens. Actuators B Chem. 2021, 345, 130338. [Google Scholar] [CrossRef]
- Urbancova, P.; Pudis, D.; Goraus, M.; Kovac, J.J. IP-Dip-Based SPR Structure for Refractive Index Sensing of Liquid Analytes. Nanomaterials 2021, 11, 1163. [Google Scholar] [CrossRef] [PubMed]












| Drude Term Parameter | Value | Oscillator 1 Parameter | Value | Oscillator 2 Parameter | Value |
|---|---|---|---|---|---|
| 1 | 3.612 | 1.423 | |||
| (nm) | 133.85 | (nm) | 309.11 | (nm) | 424.06 |
| (nm) | 27851 | (nm) | 2591.3 | (nm) | 1515.2 |
| Drude Term Parameter | Value | CP Term 1 Parameter | Value | CP Term 2 Parameter | Value |
|---|---|---|---|---|---|
| 1.129 | 33.086 | 1.659 | |||
| (nm) | 213.67 | (nm) | 1082.3 | (nm) | 496.5 |
| (nm) | 4849.8 | (nm) | 1153.2 | (nm) | 2559.7 |
| (nm) | −0.25722 | (nm) | 0.83533 |
| 147.5 nm | 3.66 nm | 38.95 nm | 2 nm | 1 mm |
| 270.9 nm | 3.11 nm | 37.93 nm | 2 nm | 1 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chylek, J.; Maniakova, P.; Hlubina, P.; Sobota, J.; Pudis, D. Highly Sensitive Plasmonic Structures Utilizing a Silicon Dioxide Overlayer. Nanomaterials 2022, 12, 3090. https://doi.org/10.3390/nano12183090
Chylek J, Maniakova P, Hlubina P, Sobota J, Pudis D. Highly Sensitive Plasmonic Structures Utilizing a Silicon Dioxide Overlayer. Nanomaterials. 2022; 12(18):3090. https://doi.org/10.3390/nano12183090
Chicago/Turabian StyleChylek, Jakub, Petra Maniakova, Petr Hlubina, Jaroslav Sobota, and Dusan Pudis. 2022. "Highly Sensitive Plasmonic Structures Utilizing a Silicon Dioxide Overlayer" Nanomaterials 12, no. 18: 3090. https://doi.org/10.3390/nano12183090
APA StyleChylek, J., Maniakova, P., Hlubina, P., Sobota, J., & Pudis, D. (2022). Highly Sensitive Plasmonic Structures Utilizing a Silicon Dioxide Overlayer. Nanomaterials, 12(18), 3090. https://doi.org/10.3390/nano12183090