How to Use Localized Surface Plasmon for Monitoring the Adsorption of Thiol Molecules on Gold Nanoparticles?
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. FTIR Analysis of MUDA Functionalized AuNPs
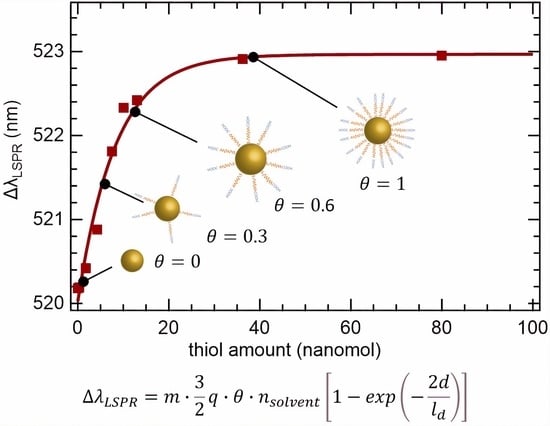
3.2. Surface Saturation Experiments
3.3. Functionalization Reaction Kinetics
3.4. Analytical and Theoretical Model for Predicting the LSPR Spectral Shift
4. Discussion
4.1. AuNP Full Functionalization—Geometrical Calculation and Experimental Determination
4.2. LSPR Shift after Full Molecular Functionalization
4.3. Kinetics and Time for Completing Nanoparticle Functionalization
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ikeda, K.; Takahashi, K.; Masuda, T.; Uosaki, K. Plasmonic enhancement of photoinduced uphill electron transfer in a molecular monolayer system. Angew. Chem. Int. Ed. 2011, 50, 1280–1284. [Google Scholar] [CrossRef] [PubMed]
- Conklin, D.; Nanayakkara, S.; Park, T.-H.; Lagadec, M.F.; Stecher, J.T.; Chen, X.; Therien, M.J.; Bonnell, D.A. Exploiting plasmon-induced hot electrons in molecular electronic devices. ACS Nano 2013, 7, 4479–4486. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Wenger, J.; Viscomi, F.N.; Le Cunff, L.; Béal, J.; Kochtcheev, S.; Yang, X.; Wiederrecht, G.P.; Colas des Francs, G.; Bisht, A.S.; et al. Two-color single hybrid plasmonic nanoemitters with real time switchable dominant emission wavelength. Nano Lett. 2015, 15, 7458–7466. [Google Scholar] [CrossRef] [PubMed]
- Amendola, V.; Pilot, R.; Frasconi, M.; Maragò, O.M.; Iatì, M.A. Surface plasmon resonance in gold nanoparticles: A review. J. Phys. Condens. Matter 2017, 29, 203002. [Google Scholar] [CrossRef] [PubMed]
- Nath, S.; Kaittanis, C.; Tinkham, A.; Perez, J.M. Dextran-coated gold nanoparticles for the assessment of antimicrobial susceptibility. Anal. Chem. 2008, 80, 1033–1038. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Wang, J.; Jiao, K.; Yang, X. Colorimetric detection of mercury ion (Hg2+) based on DNA oligonucleotides and unmodified gold nanoparticles sensing system with a tunable detection range. Biosens. Bioelectron. 2009, 24, 3153–3158. [Google Scholar] [CrossRef] [PubMed]
- Qin, G.; Zhao, S.; Huang, Y.; Jiang, J.; Liu, Y.-M. A sensitive gold nanoparticles sensing platform based on resonance energy transfer for chemiluminescence light on detection of biomolecules. Biosens. Bioelectron. 2013, 46, 119–123. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Salmain, M.; Liedberg, B.; Boujday, S. Naked Eye immunosensing of food biotoxins using gold nanoparticle-antibody bioconjugates. ACS Appl. Nano Mater. 2019, 2, 4150–4158. [Google Scholar] [CrossRef]
- Homberger, M.; Simon, U. On the application potential of gold nanoparticles in nanoelectronics and biomedicine. Philos. Trans. R. Soc. 2010, 368, 1405–1453. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Zheng, K.; Xie, J. Engineering ultrasmall water-soluble gold and silver nanoclusters for biomedical applications. Chem. Commun. 2014, 50, 5143–5155. [Google Scholar] [CrossRef] [PubMed]
- Mackey, M.A.; Ali, M.R.K.; Austin, L.A.; Near, R.D.; El-Sayed, M.A. The most effective gold nanorod size for plasmonic photothermal therapy: Theory and in vitro experiments. J. Phys. Chem. B 2014, 118, 1319–1326. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, H.; Kuwauchi, Y.; Jinschek, J.R.; Sun, K.; Tanaka, S.; Kohyama, M.; Shimada, S.; Haruta, M.; Takeda, S. Visualizing gas molecules interacting with supported nanoparticulate catalysts at reaction conditions. Science 2012, 335, 317. [Google Scholar] [CrossRef]
- Shi, X.; Ueno, K.; Oshikiri, T.; Sun, Q.; Sasaki, K.; Misawa, H. Enhanced water splitting under modal strong coupling conditions. Nat. Nanotechnol. 2018, 13, 953–958. [Google Scholar] [CrossRef]
- Alibart, F.; Pleutin, S.; Guérin, D.; Novembre, C.; Lenfant, S.; Lmimouni, K.; Gamrat, C.; Vuillaume, D. An organic nanoparticle transistor behaving as a biological spiking synapse. Adv. Funct. Mater. 2010, 20, 330–337. [Google Scholar] [CrossRef] [Green Version]
- Conklin, D.; Nanayakkara, S.; Park, T.-H.; Lagadec, M.F.; Stecher, J.T.; Therien, M.J.; Bonnell, D.A. Electronic transport in porphyrin supermolecule-gold nanoparticle assemblies. Nano Lett. 2012, 12, 2414–2419. [Google Scholar] [CrossRef]
- Pluchery, O.; Caillard, L.; Dollfus, P.; Chabal, Y.J. Gold nanoparticles on functionalized silicon substrate under Coulomb blockade regime: An experimental and theoretical investigation. J. Phys. Chem. B 2018, 122, 897–903. [Google Scholar] [CrossRef] [PubMed]
- Cho, C.-Y.; Lee, S.-J.; Song, J.-H.; Hong, S.-H.; Lee, S.-M.; Cho, Y.-H.; Park, S.-J. Enhanced optical output power of green light-emitting diodes by surface plasmon of gold nanoparticles. Appl. Phys. Lett. 2011, 98, 051106. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Liu, X.; Yan, H.; Chen, Z.; Liu, Y.; Liu, S. Highly efficient GaN-based high-power flip-chip light-emitting diodes. Opt. Express 2019, 27, A669–A692. [Google Scholar] [CrossRef]
- Kabir, D.; Forhad, T.; Ghann, W.; Richards, B.; Rahman, M.M.; Uddin, M.N.; Rakib, R.J.; Shariare, M.H.; Chowdhury, F.I.; Rabbani, M.M.; et al. Dye-sensitized solar cell with plasmonic gold nanoparticles modified photoanode. Nano Struct. Nano Objects 2021, 26, 100698. [Google Scholar] [CrossRef]
- Devid, E.J.; Martinho, P.N.; Kamalakar, M.V.; Šalitroš, I.; Prendergast, Ú.; Dayen, J.-F.; Meded, V.; Lemma, T.; González-Prieto, R.; Evers, F.; et al. Spin transition in arrays of gold nanoparticles and spin crossover molecules. ACS Nano 2015, 9, 4496–4507. [Google Scholar] [CrossRef]
- Genta, H.; Hiromi, S.; Matsushita Michio, M.; Akira, I.; Tadashi, S. Preparation and characterization of gold nanoparticles chemisorbed by π-radical thiols. Chem. Lett. 2002, 31, 1030–1031. [Google Scholar]
- Villarreal, E.; Li, G.G.; Zhang, Q.; Fu, X.; Wang, H. Nanoscale surface curvature effects on ligand–nanoparticle interactions: A plasmon-enhanced spectroscopic study of thiolated ligand adsorption, desorption, and exchange on gold nanoparticles. Nano Lett. 2017, 17, 4443–4452. [Google Scholar] [CrossRef]
- Turkevich, J.; Stevenson, P.C.; Hillier, J. A study of the nucleation and growth processes in the synthesis of colloidal gold. Discuss. Faraday Soc. 1951, 11, 55–75. [Google Scholar] [CrossRef]
- Frens, G. Controlled nucleation for regulation of particle-size in monodisperse gold suspensions. Nat. Phys. Sci. 1973, 241, 20–22. [Google Scholar] [CrossRef]
- Basu, S.; Ghosh, S.K.; Kundu, S.; Panigrahi, S.; Praharaj, S.; Pande, S.; Jana, S.; Pal, T. Biomolecule induced nanoparticle aggregation: Effect of particle size on interparticle coupling. J. Colloid Interface Sci. 2007, 313, 724–734. [Google Scholar] [CrossRef]
- Kimling, J.; Maier, M.; Okenve, B.; Kotaidis, V.; Ballot, H.; Plech, A. Turkevich method for gold nanoparticle synthesis revisited. J. Phys. Chem. B 2006, 110, 15700–15707. [Google Scholar] [CrossRef]
- Park, J.-W.; Shumaker-Parry, J.S. Structural study of citrate layers on gold nanoparticles: Role of intermolecular interactions in stabilizing nanoparticles. J. Am. Chem. Soc. 2014, 136, 1907–1921. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zeiri, O.; Neyman, A.; Stellacci, F.; Weinstock, I.A. Nucleation and island growth of alkanethiolate ligand domains on gold nanoparticles. ACS Nano 2012, 6, 629–640. [Google Scholar] [CrossRef]
- Kassam, A.; Bremner, G.; Clark, B.; Ulibarri, G.; Lennox, R.B. Place exchange reactions of alkyl thiols on gold nanoparticles. J. Am. Chem. Soc. 2006, 128, 3476–3477. [Google Scholar] [CrossRef]
- Bard, A.; Rondon, R.; Marquez, D.T.; Lanterna, A.E.; Scaiano, J.C. How fast can thiols bind to the gold nanoparticle surface? Photochem. Photobiol. 2018, 94, 1109–1115. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, E.; Tyner, K.M.; Poling, C.M.; Blacklock, J.L. Determination of nanoparticle surface coatings and nanoparticle purity using microscale thermogravimetric analysis. Anal. Chem 2014, 86, 1478–1484. [Google Scholar] [CrossRef]
- Locardi, F.; Canepa, E.; Villa, S.; Nelli, I.; Lambruschini, C.; Ferretti, M.; Canepa, F. Thermogravimetry and evolved gas analysis for the investigation of ligand-exchange reaction in thiol-functionalized gold nanoparticles. J. Anal. Appl. Pyrolysis 2018, 132, 11–18. [Google Scholar] [CrossRef]
- Bajaj, M.; Wangoo, N.; Jain, D.V.S.; Sharma, R.K. Quantification of adsorbed and dangling citrate ions on gold nanoparticle surface using thermogravimetric analysis. Sci. Rep. 2020, 10, 8213. [Google Scholar] [CrossRef] [PubMed]
- Aldewachi, H.; Woodroofe, N.; Gardiner, P. Study of the stability of functionalized gold nanoparticles for the colorimetric detection of dipeptidyl peptidase IV. Appl. Sci. 2018, 8, 2589. [Google Scholar] [CrossRef] [Green Version]
- Mazloomi-Rezvani, M.; Salami-Kalajahi, M.; Roghani-Mamaqani, H.; Pirayesh, A. Effect of surface modification with various thiol compounds on colloidal stability of gold nanoparticles. Appl. Organomet. Chem. 2018, 32, e4079. [Google Scholar] [CrossRef]
- Taladriz-Blanco, P.; Buurma, N.J.; Rodríguez-Lorenzo, L.; Pérez-Juste, J.; Liz-Marzán, L.M.; Hervés, P. Reversible assembly of metal nanoparticles induced by penicillamine. Dynamic formation of SERS hot spots. J. Mater. Chem. 2011, 21, 16880–16887. [Google Scholar] [CrossRef] [Green Version]
- Stein, B.; Zopes, D.; Schmudde, M.; Schneider, R.; Mohsen, A.; Goroncy, C.; Mathur, S.; Graf, C. Kinetics of aggregation and growth processes of PEG-stabilised mono- and multivalent gold nanoparticles in highly concentrated halide solutions. Faraday Discuss. 2015, 181, 85–102. [Google Scholar] [CrossRef] [PubMed]
- Englebienne, P.; Verhas, M.; Van Hoonacker, A. High-throughput screening using the surface plasmon resonance effect of colloidal gold nanoparticles. Analyst 2001, 126, 1645–1651. [Google Scholar] [CrossRef]
- Sardar, R.; Funston, A.M.; Mulvaney, P.; Murray, R.W. Gold nanoparticles: Past, present, and future. Langmuir 2009, 25, 13840–13851. [Google Scholar] [CrossRef]
- Ji, X.H.; Song, X.N.; Li, J.; Bai, Y.B.; Yang, W.S.; Peng, X.G. Size control of gold nanocrystals in citrate reduction: The third role of citrate. J. Amer. Chem. Soc. 2007, 129, 13939–13948. [Google Scholar] [CrossRef] [PubMed]
- Caillard, L.; Sattayaporn, S.; Lamic-Humblot, A.-F.; Casale, S.; Campbell, P.; Chabal, Y.J.; Pluchery, O. Controlling the reproducibility of coulomb blockade phenomena for gold nanoparticles on an organic monolayer/silicon system. Nanotechnology 2015, 26, 065301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pluchery, O.; Opila, R.L.; Chabal, Y.J. Wet chemical cleaning of InP surfaces investigated by in situ and ex situ infrared spectroscopy. J. Appl. Phys. 2003, 94, 2707–2715. [Google Scholar] [CrossRef]
- Busch, B.W.; Pluchery, O.; Chabal, Y.J.; Muller, D.A.; Opila, R.L.; Kwo, J.R.; Garfunkel, E. Materials characterization of alternative gate dielectrics. MRS Bull. 2002, 27, 206–211. [Google Scholar] [CrossRef] [Green Version]
- Perera, G.S.; Athukorale, S.A.; Perez, F.; Pittman, C.U.; Zhang, D. Facile displacement of citrate residues from gold nanoparticle surfaces. J. Colloid Interface Sci. 2018, 511, 335–343. [Google Scholar] [CrossRef] [PubMed]
- Louis, C.; Pluchery, O. Gold Nanoparticles for Physics, Chemistry and Biology, 2nd ed.; World Scientific Publishing Europe: London, UK, 2017. [Google Scholar]
- Bossard-Giannesini, L.; Cruguel, H.; Lacaze, E.; Pluchery, O. Plasmonic properties of gold nanoparticles on silicon substrates: Understanding Fano-like spectra observed in reflection. Appl. Phys. Lett. 2016, 109, 111901. [Google Scholar] [CrossRef] [Green Version]
- Willets, K.A.; Van Duyne, R.P. Localized surface plasmon resonance spectroscopy and sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef] [Green Version]
- Unser, S.; Bruzas, I.; He, J.; Sagle, L. Localized surface plasmon resonance biosensing: Current challenges and approaches. Sensors 2015, 15, 15684–15716. [Google Scholar] [CrossRef] [PubMed]
- Stuart, D.; Haes, A.; Yonzon, C.; Hicks, E.; Van Duyne, R.P. Biological applications of localised surface plasmonic phenomenae. IET Nanobiotechnol. 2005, 152, 13–32. [Google Scholar] [CrossRef] [PubMed]
- Zahid, A.; Hanif, M.A.; Lee, I.; Islam, M.A.; Hahn, J.R. Effect of amino, hydroxyl, and carboxyl terminal groups of alkyl chains of self-assembled monolayers on the adsorption pattern of gold nanoparticles. Surf. Interface Anal. 2019, 51, 1102–1112. [Google Scholar] [CrossRef]
- Vanderkooy, A.; Chen, Y.; Gonzaga, F.; Brook, M.A. Silica shell/gold core nanoparticles: Correlating shell thickness with the plasmonic red shift upon aggregation. ACS Appl. Mater. Interfaces 2011, 3, 3942–3947. [Google Scholar] [CrossRef]
- Haes, A.; Van Duyne, R.P. A nanoscale optical biosensor: Sensitivity and selectivity of an approach based on the localized surface plasmon resonance spectroscopy of triangular silver nanoparticles. J. Amer. Chem. Soc. 2002, 124, 10596–10604. [Google Scholar] [CrossRef]
- Dahlin, A.B.; Tegenfeldt, J.O.; Höök, F. Improving the instrumental resolution of sensors based on localized surface plasmon resonance. Anal. Chem. 2006, 78, 4416–4423. [Google Scholar] [CrossRef]
- Sannomiya, T.; Dermutz, H.; Hafner, C.; Vörös, J.; Dahlin, A.B. Electrochemistry on a localized surface plasmon resonance sensor. Langmuir 2009, 26, 7619–7626. [Google Scholar] [CrossRef]
- Watkins, W.L.; Assaf, A.; Prévot, G.; Borensztein, Y. Dichroic plasmonic films based on anisotropic au nanoparticles for enhanced sensitivity and figure of merit sensing. J. Phys. Chem. C 2021, 125, 11799–11812. [Google Scholar] [CrossRef]
- Pollitt, M.J.; Buckton, G.; Piper, R.; Brocchini, S. Measuring antibody coatings on gold nanoparticles by optical spectroscopy. RSC Adv. 2015, 5, 24521–24527. [Google Scholar] [CrossRef]
- Roether, J.; Chu, K.-Y.; Willenbacher, N.; Shen, A.Q.; Bhalla, N. Real-time monitoring of DNA immobilization and detection of DNA polymerase activity by a microfluidic nanoplasmonic platform. Biosens. Bioelectron. 2019, 142, 111528. [Google Scholar] [CrossRef]
- Messersmith, R.E.; Nusz, G.J.; Reed, S.M. Using the localized surface plasmon resonance of gold nanoparticles to monitor lipid membrane assembly and protein binding. J. Phys. Chem. C Nanomater. Interfaces 2013, 117, 26725–26733. [Google Scholar] [CrossRef] [Green Version]
- Vericat, C.; Vela, M.E.; Salvarezza, R.C. Self-assembled monolayers of alkanethiols on Au(111): Surface structures, defects and dynamics. Phys. Chem. Chem. Phys. 2005, 7, 3258–3268. [Google Scholar] [CrossRef] [PubMed]
- Goldmann, C.; Lazzari, R.; Paquez, X.; Boissière, C.; Ribot, F.; Sanchez, C.; Chanéac, C.; Portehault, D. Charge transfer at hybrid interfaces: Plasmonics of aromatic thiol-capped gold nanoparticles. ACS Nano 2015, 9, 7572–7582. [Google Scholar] [CrossRef]
- Maxwell Garnett, J.C., XII. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. 1904, 203, 385. [Google Scholar]
- Liu, X.; Atwater, M.; Wang, J.; Huo, Q. Extinction coefficient of gold nanoparticles with different sizes and different capping ligands. Colloids Surf. B Biointerfaces 2007, 58, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Badia, A.; Singh, S.; Demers, L.M.; Cuccia, L.A.; Brown, G.R.; Lennox, R.B. Self assembled monolayers on gold nanoparticles. Chem. Eur. J. 1996, 2, 359–363. [Google Scholar] [CrossRef]
- Chen, S.; Kimura, K. Synthesis and Characterization of carboxylate-modified gold nanoparticle powders dispersible in water. Langmuir 1999, 15, 1075–1082. [Google Scholar] [CrossRef]
- Hinterwirth, H.; Kappel, S.; Waitz, T.; Prohaska, T.; Lindner, W.; Lämmerhofer, M. Quantifying thiol ligand density of self-assembled monolayers on gold nanoparticles by inductively coupled plasma–mass spectrometry. ACS Nano 2013, 7, 1129–1136. [Google Scholar] [CrossRef]
- Techane, S.D.; Gamble, L.J.; Castner, D.G. Multitechnique Characterization of self-assembled carboxylic acid-terminated alkanethiol monolayers on nanoparticle and flat gold surfaces. J. Phys. Chem. C 2011, 115, 9432–9441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, W.; Durning, C.J.; Turro, N.J. Kinetics of alkanethiol adsorption on gold. Langmuir 1996, 12, 4469–4473. [Google Scholar] [CrossRef]
- Swenson, H.; Stadie, N.P. Langmuir’s theory of adsorption: A centennial review. Langmuir 2019, 35, 5409–5426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cárdenas, M.; Barauskas, J.; Schillén, K.; Brennan, J.L.; Brust, M.; Nylander, T. Thiol-specific and nonspecific interactions between dna and gold nanoparticles. Langmuir 2006, 22, 3294–3299. [Google Scholar] [CrossRef] [PubMed]
- Damos, F.S.; Luz, R.C.S.; Kubota, L.T. Determination of thickness, dielectric constant of thiol films, and kinetics of adsorption using surface plasmon resonance. Langmuir 2005, 21, 602–609. [Google Scholar] [CrossRef]






| # | [Thiol] in the Added Aliquot (µM) | nthiol Added (nmol) | [Thiol] in the Solution (µM) | λLSPR (nm) for MUDA (Measured) | λLSPR (nm) for MHDA (Measured) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 520.18 | 520.18 |
| 1 | 6 | 0.28 | 0.13 | 520.19 | 520.19 |
| 2 | 35 | 1.75 | 0.86 | 520.42 | 520.30 |
| 3 | 85 | 4.25 | 2.07 | 520.88 | 520.49 |
| 4 | 150 | 7.50 | 3.66 | 521.81 | 520.79 |
| 5 | 201 | 10.06 | 4.91 | 522.33 | 521.25 |
| 6 | 260 | 13.00 | 6.34 | 522.42 | 522.40 |
| 7 | 725 | 36.25 | 17.68 | 522.91 | 524.26 |
| 8 | 1599 | 79.97 | 39.01 | 522.95 | 524.16 |
| 9 | 2500 | 125.00 | 60.98 | 522.91 | 524.07 |
| Molecules | Length (d)/nm | nsolvent | Calc. Satur/nm | Calc. Partial Cov/nm | Meas. /nm |
|---|---|---|---|---|---|
| MUDA | 1.32 | 1.33 | 3.70 | 2.7 | |
| MHDA | 1.84 | 1.33 | 4.71 | 3.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dileseigres, A.S.; Prado, Y.; Pluchery, O. How to Use Localized Surface Plasmon for Monitoring the Adsorption of Thiol Molecules on Gold Nanoparticles? Nanomaterials 2022, 12, 292. https://doi.org/10.3390/nano12020292
Dileseigres AS, Prado Y, Pluchery O. How to Use Localized Surface Plasmon for Monitoring the Adsorption of Thiol Molecules on Gold Nanoparticles? Nanomaterials. 2022; 12(2):292. https://doi.org/10.3390/nano12020292
Chicago/Turabian StyleDileseigres, Angeline S., Yoann Prado, and Olivier Pluchery. 2022. "How to Use Localized Surface Plasmon for Monitoring the Adsorption of Thiol Molecules on Gold Nanoparticles?" Nanomaterials 12, no. 2: 292. https://doi.org/10.3390/nano12020292
APA StyleDileseigres, A. S., Prado, Y., & Pluchery, O. (2022). How to Use Localized Surface Plasmon for Monitoring the Adsorption of Thiol Molecules on Gold Nanoparticles? Nanomaterials, 12(2), 292. https://doi.org/10.3390/nano12020292