Design of A-D-A-Type Organic Third-Order Nonlinear Optical Materials Based on Benzodithiophene: A DFT Study
Abstract
:1. Introduction
2. Computational Methods
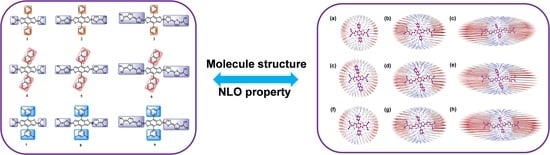
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yi, J.; Du, L.; Li, J.; Yang, L.L.; Hu, L.Y.; Huang, S.H.; Dong, Y.C.; Miao, L.L.; Wen, S.C.; Mochalin, V.N.; et al. Unleashing the potential of Ti2CTx MXene as a pulse modulator for mid-infrared fiber lasers. 2D Mater. 2019, 6, 045038–045047. [Google Scholar] [CrossRef]
- Pattipaka, S.; Joseph, A.; Bharti, G.P.; Raju, K.C.J.; Khare, A.; Pamu, D. Thickness-dependent microwave dielectric and nonlinear optical properties of Bi0.5Na0.5TiO3 thin films. Appl. Surf. Sci. 2019, 488, 391–403. [Google Scholar] [CrossRef]
- Ropagnol, X.; Kovacs, Z.; Gilicze, B.; Zhuldybina, M.; Blanchard, F.; Garcia-Rosas, C.M.; Szatmari, S.; Foldes, I.B.; Ozaki, T. Intense sub-terahertz radiation from wide-bandgap semiconductor based large-aperture photoconductive antennas pumped by UV lasers. New J. Phys. 2019, 21, 113042–113050. [Google Scholar] [CrossRef] [Green Version]
- Kuis, R.; Gougousi, T.; Basaldua, I.; Burkins, P.; Kropp, J.A.; Johnson, A.M. Engineering of large third-order nonlinearities in atomic layer deposition grown nitrogen-enriched TiO2. ACS Photonics 2019, 6, 2966–2973. [Google Scholar] [CrossRef]
- Uthayakumar, M.; Jeyakumari, A.P.; Dhandapani, A.; Shinde, V.; Arivanandhan, M. Synthesis, experimental and computational spectroscopic investigations of third-order nonlinear optical material (E)-N′-(benzo[d][1,3]dioxol-5-ylmethylene)benzo-hydrazide. J. Phys. D. Appl. Phys. 2019, 52, 395102–395113. [Google Scholar] [CrossRef]
- Dong, D.Y.; Li, Q.Z.; Hou, W.L.; Zhang, H.Q. Synthesis, nonlinear optical, magnetic and electrical properties of ultra-stable open-shell pancake bonding linked perylene diimide anion radicals π-oligomer. J. Mol. Struct. 2020, 1199, 127002–127007. [Google Scholar] [CrossRef]
- Bibi, A.; Muhammad, S.; UrRehman, S.; Bibi, S.; Bashir, S.; Ayub, K.; Adnan, M.; Khalid, M. Chemically modified quinoidal oligothiophenes for enhanced linear and third-order nonlinear optical properties. ACS Omega 2021, 6, 24602–24613. [Google Scholar] [CrossRef]
- Chang, H.J.; Bondar, M.V.; Liu, T.; Liu, X.; Singh, S.; Belfield, K.D.; Sheely, A.; Masunov, A.E.; Hagan, D.J.; van Stryland, E.W. Electronic nature of neutral and charged two-photon absorbing squaraines for fluorescence bioimaging application. ACS Omega 2019, 4, 14669–14679. [Google Scholar] [CrossRef]
- Ketavath, R.; Kattur, N.K.; Ghugal, S.G.; Kolli, H.K.; Swetha, T.; Soma, V.R.; Murali, B. Deciphering the ultrafast nonlinear optical properties and dynamics of pristine and Ni-doped CsPbBr3 colloidal two-dimensional nanocrystals. J. Phys. Chem. Lett. 2019, 10, 5577–5584. [Google Scholar] [CrossRef]
- Mbarak, H.; Kodeary, A.K.; Hamidi, S.M.; Mohajarani, E.; Zaatar, Y. Control of nonlinear refractive index of AuNPs doped with nematic liquid crystal under external electric field. Optik 2019, 198, 163299–163304. [Google Scholar] [CrossRef]
- Wang, Z.R.; Zhao, G.X.; Yan, W.Y.; Wu, K.C.; Wang, F.; Li, Q.H.; Zhang, J. Tin metal cluster compounds as new third-order nonlinear optical materials by computational study. J. Phys. Chem. Lett. 2021, 12, 7537–7544. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Ghoshal, D.; Bhattacharya, S.; Mondal, D.; Paul, B.K.; Bose, N.; Datta, P.K.; Das, S.; Basu, M. Third-order optical nonlinearity of the CuCo0.5Ti0.5O2 nanostructure under 120 fs laser irradiation. Appl. Opt. 2019, 58, 9163–9171. [Google Scholar] [CrossRef]
- Sujatha, R.A.; Flower, N.A.L.; Vinitha, G.; Sharath, R.A.; Rahulan, K.M. Structural and non-linear optical response of Er3+ doped SrMoO4 nanostructures. Appl. Surf. Sci. 2019, 490, 260–265. [Google Scholar] [CrossRef]
- Jagadale, T.C.; Murali, D.S.; Chu, S.W. Nonlinear absorption and scattering of a single plasmonic nanostructure characterized by x-scan technique. Beilstein J. Nanotechnol. 2019, 10, 2182–2191. [Google Scholar] [CrossRef] [Green Version]
- Cocca, L.H.Z.; Sciuti, L.F.; Menezes, L.B.; Kohler, M.H.; Bevilacqua, A.C.; Piquini, P.C.; Iglesias, B.A.; de Boni, L. Excited-state investigations of meso-mono-substituted-(amino-ferrocenyl) porphyrins: Experimental and theoretical approaches. J. Photoch. Photobio. A 2019, 384, 112048–112058. [Google Scholar] [CrossRef]
- Liu, Z.W.; Gan, F.; Dong, N.N.; Zhang, B.; Wang, J.; Chen, Y. Fabrication and nonlinear optical characterization of fluorinated zinc phthalocyanine covalently modified black phosphorus/PMMA films using the nanosecond Z-scan technique. J. Mater. Chem. C 2019, 7, 10789–10794. [Google Scholar] [CrossRef]
- Shelton, A.H.; Valandro, S.R.; Price, R.S.; Dubinina, G.G.; Abboud, K.A.; Wicks, G.; Rebane, A.; Younus, M.; Schanze, K.S. Stereochemical effects on platinum acetylide two-photon chromophores. J. Phys. Chem. A 2019, 123, 9382–9393. [Google Scholar] [CrossRef]
- Tong, J.; Huang, Y.; Liu, W.; Shou, M.; An, L.; Jiang, X.; Guo, P.; Han, Y.; Liang, Z.; Li, J.; et al. Optimized molecular aggregation and photophysical process synergistically promoted photovoltaic performance in low regularity benzo[c][1,2,5]thiadiazole-based medium bandgap copolymers via modulating π bridges. J. Mater. Chem. C 2022. [Google Scholar] [CrossRef]
- Xue, L.; Liu, X.; Wang, Q.; Yang, M.; Du, S.; Yang, C.; Tong, J.; Xia, Y.; Li, J. Improved Performance of Organic Solar Cells by Utilizing Green Non-Halogen Additive to Modulate Active-Layer Morphology. Energy Technol. 2022, 10, 2200504. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, X.; Li, H.; Qin, J.; Du, S.; Lu, X.; Tong, J.; Yang, C.; Li, J. Utilizing non-conjugated small-molecular tetrasodium iminodisuccinateas electron transport layer enabled improving efficiency of organic solar cells. Opt. Mater. 2022, 129, 112520. [Google Scholar] [CrossRef]
- Liu, X.; Liang, Z.; Du, S.; Niu, X.; Tong, J.; Yang, C.; Lu, X.; Bao, X.; Yan, L.; Li, J.; et al. Two compatible acceptors as an alloy model with a halogen-free solvent for efficient ternary polymer solar cells. ACS Appl. Mater. Interfaces 2022, 14, 9386–9397. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, C.; Chen, C.; Ren, Y.; Shen, H.; Tong, J.; Du, S.; Xia, Y.; Li, J. A New Alcohol-Soluble Polymer PFN-ID as Cathode Interlayer to Optimize Performance of Conventional Polymer Solar Cells by Increasing Electron Mobility. Energy Technol. 2022, 10, 2200199. [Google Scholar] [CrossRef]
- Liang, Z.; Tong, J.; Li, H.; Wang, Y.; Wang, N.; Li, J.; Yang, C.; Xia, Y. The comprehensive utilization of the synergistic effect of fullerene and non-fullerene acceptors to achieve highly efficient polymer solar cells. J. Mater. Chem. A 2019, 7, 15841–15850. [Google Scholar] [CrossRef]
- Liang, Z.; Yan, L.; Si, J.; Gong, P.; Li, X.; Liu, D.; Li, J.; Hou, X. Rational design and characterization of symmetry-breaking organic semiconductors in polymer solar cells: A theory insight of the asymmetric advantage. Materials 2021, 14, 6723. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian Inc.: Wallingford, UK, 2019. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154123. [Google Scholar] [CrossRef] [Green Version]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Hill, J.G.; Peterson, K.A. Gaussian basis sets for use in correlated molecular calculations. XI. Pseudopotential-based and all-electron relativistic basis sets for alkali metal (K-Fr) and alkaline earth (Ca-Ra) elements. J. Chem. Phys. 2017, 147, 244106–244117. [Google Scholar] [CrossRef] [Green Version]
- Prascher, B.P.; Woon, D.E.; Peterson, K.A.; Dunning, T.H.; Wilson, A.K. Gaussian basis sets for use in correlated molecular calculations. VII. Valence, core-valence, and scalar relativistic basis sets for Li, Be, Na, and Mg. Theor. Chem. Acc. 2011, 128, 69–82. [Google Scholar] [CrossRef]
- Dunning, T.H.; Peterson, K.A.; Wilson, A.K. Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited. J. Chem. Phys. 2001, 114, 9244–9253. [Google Scholar] [CrossRef] [Green Version]
- Van Mourik, T.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. VIII. Standard and augmented sextuple zeta correlation consistent basis sets for aluminum through argon. Int. J. Quantum. Chem. 2000, 76, 205–221. [Google Scholar] [CrossRef]
- Wilson, A.K.; Woon, D.E.; Peterson, K.A.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton. J. Chem. Phys. 1999, 110, 7667–7676. [Google Scholar] [CrossRef] [Green Version]
- Wilson, A.K.; van Mourik, T.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations 6. Sextuple zeta correlation consistent basis sets for boron through neon. J. Mol. Struc. Theochem. 1996, 388, 339–349. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian-basis sets for use in correlated molecular calculations 5. core-valence basis-sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef] [Green Version]
- Woon, D.E.; Dunning, T.H. Gaussian-basis sets for use in correlated molecular calculations 4. calculation of static electrical response properties. J. Chem. Phys. 1994, 100, 2975–2988. [Google Scholar] [CrossRef] [Green Version]
- Woon, D.E.; Dunning, T.H. Gaussian-basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef] [Green Version]
- Dunning, T.H. Gaussian-basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Shinde, S.S.; Sreenath, M.C.; Chitrambalam, S.; Joe, I.H.; Sekar, N. Non-linear optical properties of disperse blue 354 and disperse blue183 by DFT and Z-scan technique. Polycycl. Aromat. Comp. 2021, 41, 1531–1548. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Lu, T.; Yuan, A.; Yan, X. Potential optical molecular switch: Lithium@cyclo[18]carbon complex transforming between two stable configurations. Carbon 2022, 187, 78–85. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, T.; Yuan, A.; Wang, X.; Chen, Q.; Yan, X. Remarkable size effect on photophysical and nonlinear optical properties of all-carboatomic rings, cyclo[18]carbon and its analogues. Chem. Asian J. 2021, 16, 2267–2271. [Google Scholar] [CrossRef]









| α | Comp 1 (a.u.) | Comp 2 (a.u.) | Comp 3 (a.u.) | Comp 4 (a.u.) | Comp 5 (a.u.) | Comp 6 (a.u.) | Comp 7 (a.u.) | Comp 8 (a.u.) | Comp 9 (a.u.) |
|---|---|---|---|---|---|---|---|---|---|
| αxx | 952.08 | 2996.13 | 7979.27 | 810.35 | 3028.70 | 8018.49 | 575.88 | 3007.86 | 8023.75 |
| αxy | −34.43 | 5.86 | −69.60 | 180.20 | 292.75 | 190.93 | 186.85 | 92.34 | 15.61 |
| αyy | 489.14 | 598.37 | 726.34 | 921.301 | 834.517 | 928.69 | 865.15 | 601.55 | 726.26 |
| αxz | 0.000020 | −0.0068 | 0.02210 | −0.000030 | 0.00402 | 0.036 | −0.000020 | −0.0094 | 0.023 |
| αyz | −0.000030 | −0.0059 | −0.00531 | −0.000020 | 0.00715 | 0.010 | 0.000010 | −0.017 | −0.0052 |
| αzz | 227.12 | 290.63 | 354.587 | 308.309 | 371.897 | 437.18 | 231.75 | 293.634 | 356.31 |
| αiso | 556.12 | 1295.05 | 3020.06 | 679.986 | 1411.7 | 3128.12 | 557.59 | 1301.02 | 3035.40 |
| αaniso | 638.61 | 2565.53 | 7446.75 | 646.123 | 2510.11 | 7355.33 | 637.49 | 2579.08 | 7489.40 |
| Incident Light | Second Hyperpolarizability (γ) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Comp 1 (a.u.) | Comp 2 (a.u.) | Comp 3 (a.u.) | Comp 4 (a.u.) | Comp 5 (a.u.) | Comp 6 (a.u.) | Comp 7 (a.u.) | Comp 8 (a.u.) | Comp 9 (a.u.) | |
| ∞ (static) | 1.94 × 105 | 1.85 × 106 | 4.18 × 107 | 3.29 × 105 | 2.40 × 106 | 4.22 × 107 | 2.45 × 105 | 1.84 × 106 | 4.02 × 107 |
| 532 nm | 1.18 × 1010 | 6.70 × 107 | 1.70 × 107 | 1.02 × 109 | 9.42 × 107 | 2.59 × 107 | 1.66 × 109 | 1.68 × 108 | 2.77 × 107 |
| 1064 nm | 3.01 × 107 | 3.66 × 107 | 5.81 × 108 | 1.01 × 107 | 3.78 × 107 | 2.73 × 109 | 3.13 × 107 | 3.83 × 107 | 1.41 × 109 |
| Compound | λmax (nm) | E(eV) | f | MO Contributions a |
|---|---|---|---|---|
| 1 | 529.98 | 2.34 | 1.35 | H → L (98.07%) |
| 2 | 801.55 | 1.54 | 2.56 | H → L (97.40%) |
| 3 | 1187.25 | 1.04 | 3.34 | H → L (98.03%) |
| 4 | 544.82 | 2.27 | 1.12 | H → L (98.00%) |
| 5 | 806.19 | 1.54 | 2.51 | H → L (97.50%) |
| 6 | 1215.76 | 1.02 | 3.29 | H → L (97.90%) |
| 7 | 527.57 | 2.35 | 1.39 | H → L (98.18%) |
| 8 | 802.12 | 1.55 | 2.58 | H → L (97.50%) |
| 9 | 1218.15 | 1.01 | 3.32 | H → L (98.00%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, P.; An, L.; Tong, J.; Liu, X.; Liang, Z.; Li, J. Design of A-D-A-Type Organic Third-Order Nonlinear Optical Materials Based on Benzodithiophene: A DFT Study. Nanomaterials 2022, 12, 3700. https://doi.org/10.3390/nano12203700
Gong P, An L, Tong J, Liu X, Liang Z, Li J. Design of A-D-A-Type Organic Third-Order Nonlinear Optical Materials Based on Benzodithiophene: A DFT Study. Nanomaterials. 2022; 12(20):3700. https://doi.org/10.3390/nano12203700
Chicago/Turabian StyleGong, Pingping, Lili An, Junfeng Tong, Xinpeng Liu, Zezhou Liang, and Jianfeng Li. 2022. "Design of A-D-A-Type Organic Third-Order Nonlinear Optical Materials Based on Benzodithiophene: A DFT Study" Nanomaterials 12, no. 20: 3700. https://doi.org/10.3390/nano12203700
APA StyleGong, P., An, L., Tong, J., Liu, X., Liang, Z., & Li, J. (2022). Design of A-D-A-Type Organic Third-Order Nonlinear Optical Materials Based on Benzodithiophene: A DFT Study. Nanomaterials, 12(20), 3700. https://doi.org/10.3390/nano12203700