The Effect of Y Doping on Monoclinic, Orthorhombic, and Cubic Polymorphs of HfO2: A First Principles Study
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
3.1. Geometrical and Lattice Parameters
3.2. Ground State Cohesive Energy
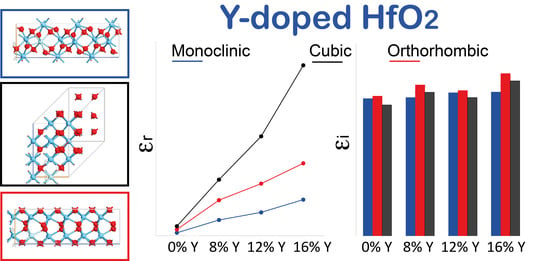
3.3. Dielectric Constant and Optical Band Gap
3.4. Refractive Index
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choi, J.; Mao, Y.; Chang, J. Development of hafnium based high-k materials—A review. Mater. Sci. Eng. R Rep. 2011, 72, 97–136. [Google Scholar] [CrossRef]
- Müller, J.; Knebel, S.; Bräuhaus, D.; Schröder, U. Insights into electrical characteristics of silicon doped hafnium oxide ferroelectric thin films. Appl. Phys. Lett. 2012, 100, 082905–082912. [Google Scholar] [CrossRef]
- Robertson, J. High dielectric constant gate oxides for metal oxide Si transistors. Rep. Prog. Phys. 2006, 69, 327–396. [Google Scholar] [CrossRef]
- Dragoman, M.L.; Modreanu, M.; Povey, I.M.; Dinescu, A.; Dragoman, D.; Di Donato, A.; Pavoni, E.; Farina, M. Wafer-scale very large memory windows in graphene monolayer/HfZrO ferroelectric capacitors. Nanotechnology 2018, 29, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Mikolajick, T.; Slesazeck, S.; Park, M.H.; Schroeder, U. Ferroelectric hafnium oxide for ferroelectric random-access memories and ferroelectric field-effect transistors. MRS Bull. 2018, 43, 340–346. [Google Scholar] [CrossRef]
- Hwang, C.S.; Dieny, B. Advanced memory—Materials for a new era of information technology. MRS Bull. 2018, 43, 330–333. [Google Scholar] [CrossRef] [Green Version]
- Jachalke, S.; Schenk, T.; Park, M.H.; Schroeder, U.; Mikolajick, T.; Stöcker, H.; Mehner, E.; Meyer, D.C. Pyroelectricity of silicon-doped hafnium oxide thin films. Appl. Phys. Lett. 2018, 112, 142901. [Google Scholar] [CrossRef]
- Ali, F.; Zhou, D.; Ali, M.; Ali, H.W.; Daaim, M.; Khan, S.; Hussain, M.M.; Sun, N. Recent Progress on Energy-Related Applications of HfO2-Based Ferroelectric and Antiferroelectric Materials. ACS Appl. Electron. Mater. 2020, 2, 2301–2317. [Google Scholar] [CrossRef]
- Mart, C.; Kämpfe, T.; Zybell, S.; Weinreich, W. Layer thickness scaling and wake-up effect of pyroelectric response in Si-doped HfO2. Appl. Phys. Lett. 2018, 112, 052905. [Google Scholar] [CrossRef]
- Park, M.H.; Kim, H.J.; Kim, Y.J.; Moon, T.; Kim, K.D.; Lee, Y.H.; Hyun, S.D.; Hwang, C.S. Giant Negative Electrocaloric Effects of Hf0.5Zr0.5O2Thin Films. Adv. Mater. 2016, 28, 7956–7961. [Google Scholar] [CrossRef]
- Xu, X.; Huang, F.-T.; Qi, Y.; Singh, S.; Rabe, K.M.; Obeysekera, D.; Yang, J.; Chu, M.-W.; Cheong, S.-W. Kinetically stabilized ferroelectricity in bulk single-crystalline HfO2:Y. Nat. Mater. 2021, 20, 826–832. [Google Scholar] [CrossRef] [PubMed]
- Huan, T.D.; Sharma, V.; Rossetti, J.G.A.; Ramprasad, R. Pathways towards ferroelectricity in hafnia. Phys. Rev. B 2014, 90, 64111. [Google Scholar] [CrossRef] [Green Version]
- Jaffe, J.E.; Bachorz, R.A.; Gutowski, M. Low-temperature polymorphs of ZrO2 and HfO2: A density-functional theory study. Phys. Rev. B 2005, 72, 144107. [Google Scholar] [CrossRef]
- Lee, C.-K.; Cho, E.; Lee, H.-S.; Hwang, C.S.; Han, S. First-Principles Study on Doping and Phase Stability of HfO2. Phys. Rev. B 2008, 78, 012102. [Google Scholar] [CrossRef]
- Jayaraman, A.; Wang, S.Y.; Sharma, S.K.; Ming, L.C. Pressure-Induced Phase Transformations in HfO2 to 50 GPa Studied by Raman Spectroscopy. Phys Rev B 1993, 48, 9205–9211. [Google Scholar] [CrossRef] [PubMed]
- Mandal, G.; Das, P. The Pressure Induced Structural Phase Transition of HfO2. AIP Conf. Proc. 2017, 1832, 030014. [Google Scholar] [CrossRef]
- Pavoni, E.; Mohebbi, E.; Stipa, P.; Mencarelli, D.; Pierantoni, L.; Laudadio, E. The Role of Zr on Monoclinic and Orthorhombic Hfx Zry O2 Systems: A First-Principles Study. Materials 2022, 15, 4175. [Google Scholar] [CrossRef]
- Materlik, R.; Künneth, C.; Falkowski, M.; Mikolajick, T.; Kersch, A. Al-, Y-, and La-Doping Effects Favoring Intrinsic and Field Induced Ferroelectricity in HfO2: A First Principles Study. J. Appl. Phys. 2018, 123, 12465–12546. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, H.J.; Moon, T.; Kim, K.D.; Hyun, S.; Park, H.W.; Lee, Y.B.; Park, M.H.; Hwang, C.S. Preparation and characterization of ferroelectric Hf0.5Zr0.5O2 thin films grown by reactive sputtering. Nanotechnology 2017, 28, 305703–305716. [Google Scholar] [CrossRef]
- Rauwel, E.; Dubourdieu, C.; Holländer, B.; Rochat, N.; Ducroquet, F.; Rossell, M.D.; van Tendeloo, G.; Pelissier, B. Stabilization of the Cubic Phase of HfO2 by Y Addition in Films Grown by Metal Organic Chemical Vapor Deposition. Appl. Phys. Lett. 2006, 89, 012902. [Google Scholar] [CrossRef]
- Chen, X.; Song, L.; You, L.; Zhao, L. Incorporation Effect of Y2O3 on the Structure and Optical Properties of HfO2 Thin Films. Appl. Surf. Sci. 2013, 271, 248–252. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, B.; Zhou, D.; Guo, X.; Li, Y.; Lu, Y.; Guo, Y. Effect of Y Concentration and Film Thickness on Microstructure and Electrical Properties of HfO2 Based Thin Films. Ceram. Int. 2021, 47, 12137–12143. [Google Scholar] [CrossRef]
- Liang, H.; Xu, J.; Zhou, D.; Ren, S. Phase Transformation and Dielectric Properties of Y Doped HfO2 Thin Films. J. Alloys Compd. 2021, 861, 158241–1582417. [Google Scholar] [CrossRef]
- Shimizu, T.; Katayama, K.; Kiguchi, T.; Akama, A.; Konno, T.J.; Sakata, O.; Funakubo, H. The Demonstration of Significant Ferroelectricity in Epitaxial Y-Doped HfO2 Film. Sci. Rep. 2016, 6, 32931–32938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shimura, R.; Mimura, T.; Tateyama, A.; Shimizu, T.; Yamada, T.; Tanaka, Y.; Inoue, Y.; Funakubo, H. Preparation of 1 Μm Thick Y-Doped HfO2ferroelectric Films on (111)Pt/TiOx/SiO2/(001)Si Substrates by a Sputtering Method and Their Ferroelectric and Piezoelectric Properties. Jpn. J. Appl. Phys. 2021, 60, 1456–1465. [Google Scholar] [CrossRef]
- Shimizu, T.; Tashiro, Y.; Mimura, T.; Kiguchi, T.; Shiraishi, T.; Konnno, T.J.; Sakata, O.; Funakubo, H. Electric-Field-Induced Ferroelectricity in 5%Y-Doped Hf0.5Zr0.5O2: Transformation from the Paraelectric Tetragonal Phase to the Ferroelectric Orthorhombic Phase. Phys. Status Solidi—Rapid Res. Lett. 2021, 15, 2000589–2000596. [Google Scholar] [CrossRef]
- Padilha, A.C.M.; McKenna, K.P. First Principles Investigation of Y2O3-Doped HfO2. J. Appl. Phys. 2019, 126, 084105–084112. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Vanderbilt, D. First-Principles Study of Structural, Vibrational, and Lattice Dielectric Properties of Hafnium Oxide. Phys. Rev. B Condens. Matter Mater. Phys. 2002, 65, 233106. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P. Density Functional Theory and the Band Gap Problem. Int. J. Quantum Chem. 1985, 28, 496–523. [Google Scholar] [CrossRef]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G.; et al. QuantumATK: An Integrated Platform of Electronic and Atomic-Scale Modelling Tools. J. Phys. Condens. Matter 2019, 32, 015901. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA Method for Ab Initio Order-N Materials Simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van Setten, M.; Giantomassi, M.; Bousquet, E.; Verstraete, M.; Hamann, D.; Gonze, X.; Rignanese, G.-M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef] [Green Version]
- Heyd, J.; Scuseria, G.E. Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187–1192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- King-Smith, R.D.; Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 1993, 47, 1651–1654. [Google Scholar] [CrossRef]
- Fan, S.-T.; Chen, Y.-W.; Liu, C.W. Strain effect on the stability in ferroelectric HfO2 simulated by first-principles calculations. J. Phys. D Appl. Phys. 2020, 53, 23LT01. [Google Scholar] [CrossRef]
- Dinh, L.N.; Chase, L.L.; Balooch, M.; Siekhaus, W.J.; Wooten, F. Optical Properties of Passivated Si Nanocrystals and SiO2 Nanostructures. Phys. Rev. B 1996, 54, 5029–5037. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Makaremi, M.; Rabczuk, T. Anisotropic mechanical and optical response and negative Poisson’s ratio in Mo2C nanomembranes revealed by first-principles simulations. Nanotechnology 2017, 28, 115705. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Shapeev, A.V.; Rabczuk, T.; Zhuang, X. Prediction of C7N6 and C9N4: Stable and strong porous carbon-nitride nanosheets with attractive electronic and optical properties. J. Mater. Chem. C 2019, 7, 10908–10917. [Google Scholar] [CrossRef] [Green Version]
- Ruh, R.; Garrett, H.J.; Domagala, R.F.; Tallan, N.M. The Svstern Zirconia-Hafnia. J. Am. Ceram. Soc. 1968, 51, 23–28. [Google Scholar] [CrossRef]
- Perevalov, T.V.; Gritsenko, V.A.; Erenburg, S.B.; Badalyan, A.M.; Wong, H.; Kim, C.W. Atomic and electronic structure of amorphous and crystalline hafnium oxide: X-ray photoelectron spectroscopy and density functional calculations. J. Appl. Phys. 2007, 101, 053704–053712. [Google Scholar] [CrossRef] [Green Version]
- Adams, D.M.; Leonard, S.; Russell, D.R.; Cernik, R.J. X-ray diffraction study of Hafnia under high pressure using synchrotron radiation. J. Phys. Chem. Solids 1991, 52, 1181–1186. [Google Scholar] [CrossRef]
- Senami, M.; Tsuchida, Y.; Fukushima, A.; Ikeda, Y.; Tachibana, A. Local Dielectric Property of Cubic, Tetragonal, and Monoclinic Hafnium Oxides. Jpn. J. Appl. Phys. 2012, 51, 031101. [Google Scholar] [CrossRef]
- Miikkulainen, V.; Leskela, M.; Ritala, M.; Puurunen, R.L. Crystallinity of inorganic films grown by atomic layer deposition: Overview and general trends. J. Appl. Phys. 2013, 113, 021201–021303. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, W.; Ma, T.P.; Stemmer, S. High-temperature phase stability of hafnium aluminate films for alternative gate dielectrics. J. Appl. Phys. 2004, 95, 3772–3777. [Google Scholar] [CrossRef] [Green Version]
- Kita, K.; Kyuno, K.; Toriumi, A. Permittivity increase of yttrium-doped HfO2 through structural phase transformation. Appl. Phys. Lett. 2005, 86, 102906. [Google Scholar] [CrossRef]
- Balog, M.; Schieber, M.; Michman, M.; Patai, S. Chemical vapor deposition and characterization of HfO2 films from organo-hafnium compounds. Thin Solid Films 1977, 41, 247–259. [Google Scholar] [CrossRef]
- Koller, D.; Tran, F.; Blaha, P. Improving the modified Becke-Johnson exchange potential. Phys. Rev. B 2012, 85, 155109. [Google Scholar] [CrossRef]





| Å | HfO2 | 8% Y:HfO2 | 12% Y:HfO2 | 16% Y:HfO2 | |
|---|---|---|---|---|---|
| Monoclinic P21/c | a | 5.116 | 5.116 | 5.116 | 5.116 |
| b | 5.172 | 5.172 | 5.172 | 5.172 | |
| c | 5.295 | 5.295 | 5.295 | 5.227 | |
| Orthorhombic Pca21 | a | 5.231 | 5.243 | 5.243 | 5.243 |
| b | 5.008 | 5.063 | 5.063 | 5.063 | |
| c | 5.052 | 5.079 | 5.079 | 5.079 | |
| Cubic Fmm | a | 5.115 | 5.115 | 5.115 | 5.115 |
| b | 5.115 | 5.115 | 5.115 | 5.115 | |
| c | 5.115 | 5.115 | 5.115 | 5.115 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavoni, E.; Mohebbi, E.; Mencarelli, D.; Stipa, P.; Laudadio, E.; Pierantoni, L. The Effect of Y Doping on Monoclinic, Orthorhombic, and Cubic Polymorphs of HfO2: A First Principles Study. Nanomaterials 2022, 12, 4324. https://doi.org/10.3390/nano12234324
Pavoni E, Mohebbi E, Mencarelli D, Stipa P, Laudadio E, Pierantoni L. The Effect of Y Doping on Monoclinic, Orthorhombic, and Cubic Polymorphs of HfO2: A First Principles Study. Nanomaterials. 2022; 12(23):4324. https://doi.org/10.3390/nano12234324
Chicago/Turabian StylePavoni, Eleonora, Elaheh Mohebbi, Davide Mencarelli, Pierluigi Stipa, Emiliano Laudadio, and Luca Pierantoni. 2022. "The Effect of Y Doping on Monoclinic, Orthorhombic, and Cubic Polymorphs of HfO2: A First Principles Study" Nanomaterials 12, no. 23: 4324. https://doi.org/10.3390/nano12234324
APA StylePavoni, E., Mohebbi, E., Mencarelli, D., Stipa, P., Laudadio, E., & Pierantoni, L. (2022). The Effect of Y Doping on Monoclinic, Orthorhombic, and Cubic Polymorphs of HfO2: A First Principles Study. Nanomaterials, 12(23), 4324. https://doi.org/10.3390/nano12234324