Elastic Strain Relaxation of Phase Boundary of α′ Nanoscale Phase Mediated via the Point Defects Loop under Normal Strain
Abstract
:1. Introduction
2. Model and Methods
2.1. Elastic Strain Including Vacancy and Interstitial Atoms
2.2. Free Energy
2.3. Phase-Field Model
2.4. Numerical Calculation
3. Results and Discussion
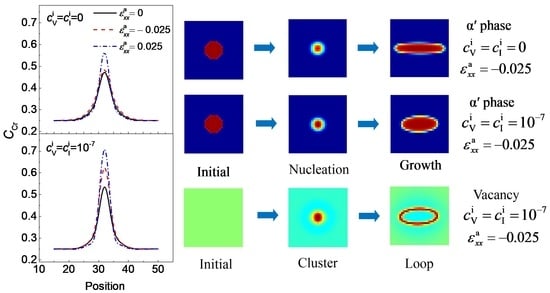
3.1. α′ Phase Evolution with a Point Defects Loop under Normal Strain
3.2. Concentration Evolution of the α′ Phase with the Effects of Point Defects, Strains and Temperature
3.3. Splitting of the α′ Phase with Defects Loop under Normal Strain
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Clouet, E.; Varvenne, C.; Jourdan, T. Elastic modeling of point-defects and their interaction. Comput. Mater. Sci. 2018, 147, 49–63. [Google Scholar] [CrossRef] [Green Version]
- Soisson, F.; Jourdan, T. Radiation-accelerated precipitation in Fe–Cr alloys. Acta Mater. 2016, 103, 870–881. [Google Scholar] [CrossRef]
- Grönhagen, K.; Ågren, J.; Odéna, M. Phase-field modelling of spinodal decomposition in TiAlN including the effect of metal vacancies. Scr. Mater. 2015, 95, 42–45. [Google Scholar] [CrossRef]
- Liang, L.Y.; Mei, Z.G.; Kim, Y.S.; Anitescu, M.; Yacout, A.M. Three-dimensional phase-field simulations of intragranular gas bubble evolution in irradiated U–Mo fuel. Comput. Mater. Sci. 2018, 145, 86–95. [Google Scholar] [CrossRef]
- Eshelby, J.D. The continuum theory of lattice defects. Solid State Phys. 1956, 3, 79–144. [Google Scholar] [CrossRef]
- Sugathan, S.; Bhattacharya, S. A phase-field study of elastic stress effects on phase separation in ternary alloys. Comput. Mater. Sci. 2020, 172, 109284. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.Y.; Xu, P.; Liu, Q.B. Effects of stress-induced solid phase transformations on residual stress in laser cladding a Fe–Mn–Si–Cr–Ni alloy coating. Mater. Des. 2020, 193, 108824. [Google Scholar] [CrossRef]
- Apte, A.; Kochat, V.; Rajak, P.; Krishnamoorthy, A.; Manimunda, P.; Hachtel, J.A.; Idrobo, J.C.; Amanulla, S.A.S.; Vashishta, P.; Nakano, A.; et al. Structural phase transformation in strained monolayer MoWSe2 alloy. ACS Nano 2018, 12, 3468–3476. [Google Scholar] [CrossRef]
- Fratzl, P.; Penrose, O.; Lebowitz, J.L. Modeling of phase separation in alloys with coherent elastic misfit. J. Stat. Phys. 1999, 95, 1429–1503. [Google Scholar] [CrossRef] [Green Version]
- Tien, J.K.; Copley, S.M. The effect of orientation and sense of applied uniaxial stress on the morphology of coherent gamma prime precipitates in stress annealed nickel-base superalloy crystals. Metall. Trans. 1971, 2, 543–553. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.S.; Shi, S.J.; Tong, X.W.; Yan, Z.W. Phase-field simulation of γ’ precipitates rafting and creep property of Co-base superalloys. Mater. Des. 2020, 196, 109077. [Google Scholar] [CrossRef]
- Sakaguchia, M.; Okazaki, M. Distinctive role of plastic and creep strain in directional coarsening of a Ni-base single crystal superalloy. Mater. Sci. Eng. A 2018, 710, 121–128. [Google Scholar] [CrossRef]
- Prikhodko, S.V.; Ardell, A.J. Coarsening of γ′ in Ni–Al alloys aged under uniaxial compression: I. Early-stage kinetics. Acta Mater. 2003, 51, 5001–5012. [Google Scholar] [CrossRef]
- Ardell, A.J.; Prikhodko, S.V. Coarsening of γ′ in Ni–Al alloys aged under uniaxial compression: II. Diffusion under stress and retardation of coarsening kinetics. Acta Mater. 2003, 51, 5013–5019. [Google Scholar] [CrossRef]
- Tong, X.W.; Li, Y.S.; Yan, Z.W.; Wang, D. Phase-field simulation of effects of normal strain on the morphology and kinetics evolution of nanoscale phase. J. Mater. Res. Technol. 2020, 9, 2063–2071. [Google Scholar] [CrossRef]
- Maqbool, S.; Li, Y.S.; Muhammad, S.; Yan, Z.W. Phase-feld simulation of Cu enriched nanoparticles with variation of defects migration energy under neutron irradiation. Model. Simul. Mater. Sci. Eng. 2021, 29, 085011. [Google Scholar] [CrossRef]
- Yan, Z.W.; Shi, S.J.; Li, Y.S.; Chen, J.; Maqbool, S. Vacancy and interstitial atom evolution with the separation of the nanoscale phase in Fe–Cr alloys: Phase-field simulations. Phys Chem. Chem. Phys. 2020, 22, 3611–3619. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Huang, X.F.; He, K.; Wang, H. Precipitation behavior and age hardening effect of the precipitates in a Fe-13Cr-4Al-2Mo-1.2Nb alloy. Mater. Charact. 2021, 173, 110918. [Google Scholar] [CrossRef]
- Kim, H.; Subramanian, G.O.; Kim, C.; Jang, H.; Jang, C. 400 °C aging embrittlement of FeCrAl alloys: Microstructure and fracture behavior. Mater. Sci. Eng. A 2019, 743, 159–167. [Google Scholar] [CrossRef]
- Zhu, L.H.; Li, Y.S.; Liu, C.W.; Chen, S.; Shi, S.J.; Jin, S.S. Effect of applied strain on phase separation of Fe–28 at. % Cr alloy: 3D phase-field simulation. Model. Simul. Mater. Sci. Eng. 2018, 26, 035015. [Google Scholar] [CrossRef]
- Doi, M.; Miyazaki, T.; Wakatsuki, T. The effect of elastic interaction energy on the morphology of γ′ precipitates in nickel-based alloys. Mater. Sci. Eng. 1984, 67, 247–253. [Google Scholar] [CrossRef]
- Yang, M.; Wei, H.; Zhang, J.; Zhao, Y.; Jin, T.; Liu, L.; Sun, X.F. Phase-field study on effects of antiphase domain and elastic energy on evolution of γ′ precipitates in nickel-based superalloys. Comput. Mater. Sci. 2017, 129, 211–219. [Google Scholar] [CrossRef]
- Lee, J.K. A study on coherency strain and precipitate morphologyvia a discrete atom method. Metall. Mater. Trans. A 1996, 27, 1449–1459. [Google Scholar] [CrossRef]
- Li, D.Y.; Chen, L.Q. Shape evolution and splitting of coherent particles under applied stresses. Acta Mater. 1999, 47, 247–257. [Google Scholar] [CrossRef]
- Khachaturyan, A.G. Theory of Structural Transformations in Solids; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Smirnova, D.E.; Kuksin, A.Y.; Starikov, S.V. Investigation of point defects diffusion in bcc uranium and U–Mo alloys. J. Nucl. Mater. 2015, 45, 304–311. [Google Scholar] [CrossRef]
- Hu, S.Y.; Chen, L.Q. A phase-field model for evolving microstructures with strong elastic inhomogeneity. Acta Mater. 2001, 49, 1879–1890. [Google Scholar] [CrossRef]
- Li, Y.S.; Li, S.X.; Zhang, T.Y. Effect of dislocations on spinodal decomposition in Fe–Cr alloys. J Nucl Mater. 2009, 395, 120–130. [Google Scholar] [CrossRef]
- Wang, J.J.; Yang, T.N.; Zorn, J.A.; Wang, E.; Irwin, J.L.; Lindemann, S.; Rzchowski, M.S.; Hu, J.M.; Eom, C.B.; Chen, L.Q. Strain anisotropy and magnetic domain structures in multiferroic heterostructures: High-throughput finite-element and phase-field studies. Acta. Mater. 2019, 176, 73–83. [Google Scholar] [CrossRef]
- Cahn, J.W. Phase separation by spinodal decomposition in isotropic system. J. Chem. Phys. 1965, 42, 93–99. [Google Scholar] [CrossRef]
- Andersson, J.O.; Sundman, B. Thermodynamic properties of the Cr–Fe system. Calphad 1987, 11, 83–92. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Ding, J.H.; Huang, S.S.; Zhao, J.J.; Wang, Y.Z. Mesoscale modeling of irradiation damage evolution in bcc iron and vanadium: A comparative study. Fusion Eng. Des. 2018, 137, 303–311. [Google Scholar] [CrossRef]
- Dinsdale, T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Millett, P.C.; Azab, A.E.; Rokkam, S.; Tonks, M.; Wolf, D. Phase-field simulation of irradiated metals Part I: Void kinetics. Comput. Mater. Sci. 2011, 50, 949–959. [Google Scholar] [CrossRef]
- Jiang, Y.B.; Liu, W.B.; Li, W.J.; Sun, Z.Y.; Xin, Y.; Chen, P.H.; Yun, D. Phase-field simulation of the interaction between intergranular voids and grain boundaries during radiation in UO2. Comput. Mater. Sci. 2021, 188, 110176. [Google Scholar] [CrossRef]
- Mohanty, R.R.; Guyer, J.E.; Sohn, Y. Diffusion under temperature gradient: A phase-field model study. J. Appl. Phys. 2009, 106, 034912. [Google Scholar] [CrossRef]
- Okita, T.; Sekimura, N.; Garner, F.A. Effects of dpa rate on swelling in neutron-irradiated Fe–Cr and Fe–Cr–Mo alloys. J. Nucl. Mater. 2011, 417, 944–948. [Google Scholar] [CrossRef]
- Gao, Y.P.; Zhang, Y.F.; Schwen, D.; Jiang, C.; Sun, C.; Gan, J. Formation and self-organization of void superlattices under irradiation: A phase field study. Materialia 2018, 1, 78–88. [Google Scholar] [CrossRef]
- Xiong, W.; Selleby, M.; Chen, Q.; Odqvist, J.; Du, Y. Phase equilibria and thermodynamic properties in the Fe–Cr system. Crit. Rev. Solid State Mater. Sci. 2010, 35, 125–152. [Google Scholar] [CrossRef]
- Barkar, T.; Höglund, L.; Odqvist, J.; Ågren, J. Effect of concentration dependent gradient energy coefficient on spinodal decomposition in the Fe–Cr system. Comput. Mater. Sci. 2018, 143, 446–453. [Google Scholar] [CrossRef]
- Zhu, L.H.; Li, Y.S.; Shi, S.J.; Yan, Z.W.; Chen, J.; Maqbool, S. Morphology and Kinetics Evolution of Nanoscale Phase in Fe–Cr Alloys under External Strain. Nanomaterials 2019, 9, 294. [Google Scholar] [CrossRef]
- Cottua, M.; Appolaire, B.; Finel, A.; Bouar, Y.L. Microstructure evolution under [110] creep in Ni-base superalloys. Acta Mater. 2021, 212, 116851. [Google Scholar] [CrossRef]
- Mughrabi, H. The importance of sign and magnitude of γ/γ′ lattice misfit in superalloys with special reference to the new γ′-hardened cobalt-base superalloys. Acta Mater. 2014, 81, 21–29. [Google Scholar] [CrossRef]
- Wang, J.C.; Osawa, M.; Yokokawa, T.; Harada, H.; Enomotoc, M. Modeling the microstructural evolution of Ni-base superalloys by phase field method combined with CALPHAD and CVM. Comput. Mater. Sci. 2007, 39, 871–879. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhu, H.; Zhang, L.; Cheng, X.L. Phase decomposition and morphology characteristic in thermal aging Fe–Cr alloys under applied strain: A phase-field simulation. J. Nucl. Mater. 2012, 429, 13–18. [Google Scholar] [CrossRef]
- Anento, N.; Serra, A.; Osetsky, Y. Effect of nickel on point defects diffusion in Fe–Ni alloys. Acta Mater. 2017, 132, 367–373. [Google Scholar] [CrossRef]
- Rachbauer, R.; Massl, S.; Stergar, E.; Holec, D.; Kiener, D.; Keckes, J.; Patscheider, J.; Stiefel, M.; Leitner, H.; Mayrhofer, P.H. Decomposition pathways in age hardening of Ti–Al–N films. J. Appl. Phys. 2011, 110, 023515. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, D.; Banerjee, R.; Wang, Y. Formation of split patterns of γ′ precipitates in Ni-Al via particle aggregation. Scr. Mater. 1999, 41, 1023–1030. [Google Scholar] [CrossRef]
- Yoo, Y.S.; Yoon, D.Y.; Henry, M.F. The effect of elastic misfit strain on the morphological evolution of γ′-precipitates in a model Ni-base superalloy. Met. Mater. 1995, 1, 47–61. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Z.; Wang, Y.X. Elastic strain energy induced split during precipitation in alloys. J. Alloy Compd. 2016, 661, 349–356. [Google Scholar] [CrossRef]













| 0 | −0.025 | 0.025 | 0 | −0.025 | 0.025 | |
| - | 0.01 | 0.10 | - | 0.09 | 0.18 | |
| - | 0.021 | 0.208 | - | 0.164 | 0.327 | |
| −0.025 | 0.025 | −0.025 | 0.025 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Shi, S.; Sang, P.; Li, K.; Qin, Q.; Li, Y. Elastic Strain Relaxation of Phase Boundary of α′ Nanoscale Phase Mediated via the Point Defects Loop under Normal Strain. Nanomaterials 2023, 13, 456. https://doi.org/10.3390/nano13030456
Yan Z, Shi S, Sang P, Li K, Qin Q, Li Y. Elastic Strain Relaxation of Phase Boundary of α′ Nanoscale Phase Mediated via the Point Defects Loop under Normal Strain. Nanomaterials. 2023; 13(3):456. https://doi.org/10.3390/nano13030456
Chicago/Turabian StyleYan, Zhengwei, Shujing Shi, Peng Sang, Kaiyue Li, Qingqing Qin, and Yongsheng Li. 2023. "Elastic Strain Relaxation of Phase Boundary of α′ Nanoscale Phase Mediated via the Point Defects Loop under Normal Strain" Nanomaterials 13, no. 3: 456. https://doi.org/10.3390/nano13030456
APA StyleYan, Z., Shi, S., Sang, P., Li, K., Qin, Q., & Li, Y. (2023). Elastic Strain Relaxation of Phase Boundary of α′ Nanoscale Phase Mediated via the Point Defects Loop under Normal Strain. Nanomaterials, 13(3), 456. https://doi.org/10.3390/nano13030456