Biaxial Structures of Localized Deformations and Line-like Distortions in Effectively 2D Nematic Films
Abstract
:1. Introduction
2. Phenomenological Model of Nematic Ordering
2.1. Order Parameter
2.2. Order Reconstruction
2.3. 2D Model of Nematic Ordering
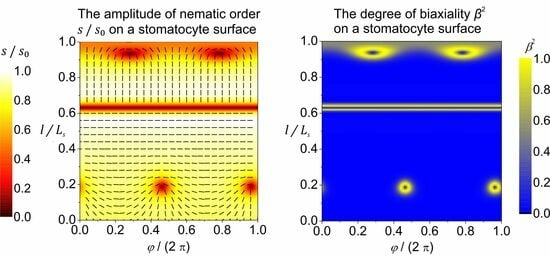
3. Results and Discussion
Coupling between Topological Defect and Nanoparticles
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kleman, M.; Laverntovich, O.D. Soft Matter Physics: An Introduction; Springer Science & BusinessMedia: New York, NY, USA, 2007. [Google Scholar]
- Palffy-Muhoray, P. The diverse world of liquid crystals. Phys. Today 2007, 6, 54–60. [Google Scholar] [CrossRef]
- Mesarec, L.; Góźdź, W.; Iglič, A.; Kralj-Iglič, V.; Virga, E.G.; Kralj, S. Normal red blood cells’ shape stabilized by membrane’s in-plane ordering. Sci. Rep. 2019, 9, 19742. [Google Scholar] [CrossRef] [PubMed]
- Kralj-Iglič, V.; Heinrich, V.; Svetina, S.; Žeks, B. Free energy of closed membrane with anisotropic inclusions. Eur. Phys. J. B 1999, 10, 5–8. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Babnik, B.; Gauger, D.R.; May, S.; Iglič, A. Quadrupolar ordering of phospholipid molecules in narrow necks of phospholipid vesicles. J. Stat. Phys. 2006, 125, 727–752. [Google Scholar] [CrossRef]
- Fournier, J. Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions. Phys. Rev. Lett. 1996, 76, 4436–4439. [Google Scholar] [CrossRef]
- Fournier, J.B.; Galatola, P. Bilayer Membranes with 2D-Nematic Order of the Surfactant Polar Heads. Braz. J. Phys. 1998, 28, 329–338. [Google Scholar] [CrossRef]
- Vyas, P.; Kumar, P.S.; Das, S.L. Sorting of proteins with shape and curvature anisotropy on a lipid bilayer tube. Soft Matter 2022, 18, 1653–1665. [Google Scholar] [CrossRef]
- Kumar, G.; Duggisetty, S.C.; Srivastava, A. A review of mechanics-based mesoscopic membrane remodeling methods: Capturing both the physics and the chemical diversity. J. Membr. Biol. 2022, 255, 757–777. [Google Scholar] [CrossRef] [PubMed]
- Mesarec, L.; Góźdź, W.; Kralj-Iglič, V.; Kralj, S.; Iglič, A. Coupling of nematic in-plane orientational ordering and equilibrium shapes of closed flexible nematic shells. Sci. Rep. 2023, 13, 10663. [Google Scholar] [CrossRef]
- Mahapatra, A.; Uysalel, C.; Rangamani, P. The mechanics and thermodynamics of tubule formation in biological membranes. J. Membr. Biol. 2021, 254, 273–291. [Google Scholar] [CrossRef]
- Alimohamadi, H.; Bell, M.K.; Halpain, S.; Rangamani, P. Mechanical Principles Governing the Shapes of Dendritic Spines. Front. Physiol. 2021, 12, 657074. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Leon, T.; Koning, V.; Devaiah, K.B.S.; Vitelli, V.; Fernandez-Nieves, A. Frustrated nematic order in spherical geometries. Nat. Phys. 2011, 7, 391–394. [Google Scholar] [CrossRef]
- Sačej, G.; Zannoni, C. Controlling surface defect valence in colloids. Phys. Rev. Lett. 2008, 100, 197802. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.R. Toward a tetravalent chemistry of colloids. Nano Lett. 2002, 2, 1125–1129. [Google Scholar] [CrossRef]
- Zurek, W.H. Cosmological experiments in superfluid helium? Nature 1985, 317, 505–508. [Google Scholar] [CrossRef]
- Lavrentovich, O.D. Topological defects in dispersed liquid crystals, or words and worlds around liquid crystal drops. Liq. Cryst. 1998, 24, 117–126. [Google Scholar] [CrossRef]
- Schopohl, N.; Sluckin, T.J. Defect Core Structure in Nematic Liquid Crystals. Phys. Rev. Lett. 1987, 59, 2582–2584. [Google Scholar] [CrossRef] [PubMed]
- Palffy-Muhoray, P.; Gartland, E.C.; Kelly, J.R. A new configurational transition in inhomogeneous nematics. Liq. Cryst. 1994, 16, 713–718. [Google Scholar] [CrossRef]
- Lombardo, G.; Amoddeo, A.; Hamdi, R.; Abey, H.; Barberi, R. Biaxial surface order dynamics in calamitic nematics. Eur. Phys. J. E 2012, 35, 32. [Google Scholar] [CrossRef]
- Bisi, F.; Garland, E.C.; Rosso, R.; Virga, E.G. Order reconstruction in frustrated nematic twist cells. Phys. Rev. E 2003, 68, 021707. [Google Scholar] [CrossRef]
- Rosso, R.; Virga, E.G. Metastable nematic hedgehogs. J. Phys. A Math. Gen. 1996, 29, 4247–4264. [Google Scholar] [CrossRef]
- Kamien, R.D. The geometry of soft materials: A primer. Rev. Mod. Phys. 2002, 74, 953–971. [Google Scholar] [CrossRef]
- Svenšek, D.; Žumer, S. Instability Modes of High-Strength Disclinations in Nematics. Phys. Rev. E 2004, 70, 061707. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Liu, M.; Zhou, X.; Zhang, Z. Decomposition of Topological Defects in Liquid Crystal Wells with Homeotropic Anchoring. Liq. Cryst. 2021, 48, 1929–1939. [Google Scholar] [CrossRef]
- Vitelli, V.; Turner, A.M. Anomalous coupling between topological defects and curvature. Phys. Rev. Lett. 2004, 93, 215301. [Google Scholar] [CrossRef]
- Mesarec, L.; Góźdź, W.; Iglič, A.; Kralj, S. Effective topological charge cancellation mechanism. Sci. Rep. 2016, 6, 27117. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Svetina, S.; Žekš, B. Shapes of bilayer vesicles with membrane-embedded molecules. Eur. Biophys. J. 1996, 24, 311–321. [Google Scholar] [CrossRef]
- Selinger, R.L.B.; Konya, A.; Travesset, A.; Selinger, J.V. Monte Carlo studies of the XY model on two-dimensional curved surfaces. J. Phys. Chem. B 2011, 115, 13989–13993. [Google Scholar] [CrossRef]
- Napoli, G.; Vergori, L. Extrinsic curvature effects on nematic shells. Phys. Rev. Lett. 2012, 108, 207803. [Google Scholar] [CrossRef]
- Kralj-Iglič, V. Stability of Membranous Nanostructures: A Possible Key Mechanism in Cancer Progression. Int. J. Nanomed. 2012, 7, 3579–3596. [Google Scholar] [CrossRef]
- Fischer, T.M. Bending stiffness of lipid bilayers. II. Spontaneous curvature of the monolayers. J. Phys. II 1992, 2, 327–336. [Google Scholar] [CrossRef]
- Fischer, T.M. Bending stiffness of lipid bilayers. III. Gaussian curvature. J. Phys. II 1992, 2, 337–343. [Google Scholar] [CrossRef]
- Fischer, T.M. Bending stiffness of lipid bilayers: IV. Interpretation of Red Cell Shape Change. Biophys. J. 1993, 65, 687–692. [Google Scholar] [CrossRef] [PubMed]
- Fischer, T.M. Bending stiffness of lipid bilayers. V. Comparison of Two Formulations. J. Phys. Chem. B 1993, 3, 1795–1805. [Google Scholar] [CrossRef]
- Perutková, Š.; Kralj-Iglič, V.; Frank, M.; Iglič, A. Mechanical stability of membrane nanotubular protrusions influenced by attachment of flexible rod-like proteins. J. Biomech. 2010, 43, 1612–1617. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, P.; Wiese, W.; Hess, S. Stability and instability of uniaxial alignment against biaxial distortions in the isotropic and nematic phases of liquid crystals. J. Non-Equilib. Thermodyn. 1992, 17, 153–170. [Google Scholar] [CrossRef]
- Kralj, S.; Virga, E.G.; Žumer, S. Biaxial torus around nematic point defects. Phys. Rev. E 1999, 60, 1858–1866. [Google Scholar] [CrossRef]
- Kralj, S.; Rosso, R.; Virga, E.G. Finite-size effects on order reconstruction around nematic defects. Phys. Rev. E 2010, 81, 021702. [Google Scholar] [CrossRef]
- Hamdi, R.; Lombardo, G.; Santo, M.P.; Barberi, R. Biaxial Coherence Length in a Nematic π-Cell. Eur. Phys. J. E 2013, 36, 115. [Google Scholar] [CrossRef]
- Lyuksyutov, I.F. Topological instability of singularities at small distances. Zh. Eksp. Teor. Fiz. 1978, 75, 358–360. [Google Scholar]
- Ambrožič, M.; Bisi, F.; Virga, E.G. Director Reorientation and Order Reconstruction: Competing Mechanisms in a Nematic Cell. Contin. Mech. Thermodyn. 2008, 20, 193–218. [Google Scholar] [CrossRef]
- Rosso, R.; Virga, E.G.; Kralj, S. Parallel transport and defects on nematic shells. Contin. Mech. Thermodyn. 2012, 24, 643–664. [Google Scholar] [CrossRef]
- Do Carmo, M.P. Differential Geometry of Curves and Surfaces: Revised and Updated Second Edition; Courier Dover Publications: Mineola, NY, USA, 2016. [Google Scholar]
- Kikuchi, H.; Yokota, M.; Hisakado, Y.; Yang, H.; Kajiyama, T. Polymer-stabilized liquid crystal blue phases. Nat. Mater. 2002, 1, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, H.; Tanaka, Y.; Kawamoto, K.; Kubo, H.; Tsuda, T.; Fujii, A.; Kuwabata, S.; Kikuchi, H.; Ozaki, M. Nanoparticle-stabilized cholesteric blue phases. Appl. Phys. Express 2009, 2, 121501. [Google Scholar] [CrossRef]
- Yan, J.; Wu, S.T. Polymer-Stabilized Blue Phase Liquid Crystals: A Tutorial. Opt. Mater. Express 2011, 1, 1527–1535. [Google Scholar] [CrossRef]
- Cordoyiannis, G.; Jampani, V.S.R.; Kralj, S.; Dhara, S.; Tzitzios, V.; Basina, G.; Nounesis, G.; Kutnjak, Z.; Tripathi, C.S.P.; Losada-Perez, P.; et al. Different modulated structures of topological defects stabilized by adaptive targeting nanoparticles. Soft Matter 2013, 9, 3956–3964. [Google Scholar] [CrossRef]
- Schopohl, N.; Sluckin, T.J. Hedgehog Structure in Nematic and Magnetic Systems. J. Phys. 1988, 49, 1097–1101. [Google Scholar] [CrossRef]
- Zhou, S.; Shiyanovskii, S.V.; Park, H.S.; Lavrentovich, O.D. Fine Structure of the Topological Defect Cores Studied for Disclinations in Lyotropic Chromonic Liquid Crystals. Nat. Commun. 2017, 8, 14974. [Google Scholar] [CrossRef]
- Ambrožič, M.; Kralj, S.; Virga, E.G. Defect-enhanced nematic surface order reconstruction. Phys. Rev. E 2007, 75, 031708. [Google Scholar] [CrossRef]
- Góźdź, W.T. Deformations of Lipid Vesicles Induced by Attached Spherical Particles. Langmuir 2007, 23, 5665–5669. [Google Scholar] [CrossRef]
- Cannon, G.J.; Swanson, J.A. The Macrophage Capacity for Phagocytosis. J. Cell Sci. 1992, 101, 907–913. [Google Scholar] [CrossRef] [PubMed]
- Kumari, S.; Mg, S.; Mayor, S. Endocytosis Unplugged: Multiple Ways to Enter the Cell. Cell Res. 2010, 20, 256–275. [Google Scholar] [CrossRef] [PubMed]
- Flannagan, R.S.; Jaumouillé, V.; Grinstein, S. The Cell Biology of Phagocytosis. Annu. Rev. Pathol. Mech. Dis. 2012, 7, 61–98. [Google Scholar] [CrossRef] [PubMed]
- Ellinger, I.; Pietschmann, P. Endocytosis in Health and Disease—A Thematic Issue Dedicated to Renate Fuchs. Wien. Med. Wochenschr. 2016, 166, 193–195. [Google Scholar] [CrossRef]
- Mylvaganam, S.; Freeman, S.A.; Grinstein, S. The Cytoskeleton in Phagocytosis and Macropinocytosis. Curr. Biol. 2021, 31, R619–R632. [Google Scholar] [CrossRef] [PubMed]
- Niedergang, F.; Chavrier, P. Signaling and Membrane Dynamics During Phagocytosis: Many Roads Lead to the Phagosome. Curr. Opin. Cell Biol. 2004, 16, 422–428. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Liu, X. Computational Study on the Uptake of Soft Nanoparticles and Nanoparticle Cluster by Cells. J. Appl. Phys. 2022, 132, 174702. [Google Scholar] [CrossRef]
- Gao, H.; Shi, W.; Freund, L.B. Mechanics of Receptor-Mediated Endocytosis. Proc. Natl. Acad. Sci. USA 2005, 102, 9469–9474. [Google Scholar] [CrossRef]
- Richards, D.M.; Endres, R.G. The mechanism of phagocytosis: Two stages of engulfment. Biophys. J. 2014, 107, 1542–1553. [Google Scholar] [CrossRef]
- Richards, D.M.; Endres, R.G. Target shape dependence in a simple model of receptor-mediated endocytosis and phagocytosis. Proc. Natl. Acad. Sci. USA 2016, 113, 6113–6118. [Google Scholar] [CrossRef]
- Frey, F.; Ziebert, F.; Schwarz, U.S. Stochastic Dynamics of Nanoparticle and Virus Uptake. Phys. Rev. Lett. 2019, 122, 088102. [Google Scholar] [CrossRef] [PubMed]
- Van Zon, J.S.; Tzircotis, G.; Caron, E.; Howard, M. A Mechanical Bottleneck Explains the Variation in Cup Growth During FcγR Phagocytosis. Mol. Syst. Biol. 2009, 5, 298. [Google Scholar] [CrossRef] [PubMed]
- Khosravanizadeh, A.; Sens, P.; Mohammad-Rafiee, F. Wrapping of a Nanowire by a Supported Lipid Membrane. Soft Matter 2019, 15, 7490–7500. [Google Scholar] [CrossRef] [PubMed]
- Bahrami, A.H. Orientational Changes and Impaired Internalization of Ellipsoidal Nanoparticles by Vesicle Membranes. Soft Matter 2013, 9, 8642–8646. [Google Scholar] [CrossRef]
- Sadhu, R.K.; Barger, S.R.; Penič, S.; Iglič, A.; Krendel, M.; Gauthier, N.C.; Gov, N.S. A Theoretical Model of Efficient Phagocytosis Driven by Curved Membrane Proteins and Active Cytoskeleton Forces. Soft Matter 2023, 19, 31–43. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R. Remodeling of Membrane Shape and Topology by Curvature Elasticity and Membrane Tension. Adv. Biol. 2022, 6, 2101020. [Google Scholar] [CrossRef] [PubMed]
- Prakash, S.; Kumbhojkar, N.; Clegg, J.R.; Mitragotri, S. Cell-Bound Nanoparticles for Tissue Targeting and Immunotherapy: Engineering of the Particle–Membrane Interface. Curr. Opin. Colloid Interface Sci. 2021, 52, 101408. [Google Scholar] [CrossRef]
- Coursault, D.; Grand, J.; Zappone, B.; Ayeb, H.; Lévi, G.; Félidj, N.; Lacaze, E. Linear self-assembly of nanoparticles within liquid crystal defect arrays. Adv. Mater. 2012, 24, 1461–1465. [Google Scholar] [CrossRef]
- Harkai, S.; Murray, B.S.; Rosenblatt, C.; Kralj, S. Electric field-driven reconfigurable multistable topological defect patterns. Phys. Rev. Res. 2020, 2, 013176. [Google Scholar] [CrossRef]
- Guillamat, P.; Blanch-Mercader, C.; Pernollet, G.; Kruse, K.; Roux, A. Integer Topological Defects Organize Stresses Driving Tissue Morphogenesis. Nat. Mater. 2022, 21, 588–597. [Google Scholar] [CrossRef]
- Saw, T.B.; Doostmohammadi, A.; Nier, V.; Kocgozlu, L.; Thampi, S.; Toyama, Y.; Marcq, P.; Lim, C.T.; Yeomans, J.M.; Ladoux, B. Topological Defects in Epithelia Govern Cell Death and Extrusion. Nat. Chem. 2017, 544, 212–216. [Google Scholar] [CrossRef] [PubMed]
- Pujals, S.; Miyamae, H.; Afonin, S.; Murayama, T.; Hirose, H.; Nakase, I.; Taniuchi, K.; Umeda, M.; Sakamoto, K.; Ulrich, A.S.; et al. Curvature Engineering: Positive Membrane Curvature Induced by Epsin N-Terminal Peptide Boosts Internalization of Octaarginine. ACS Chem. Biol. 2013, 8, 1894–1899. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, K.; Aburai, K.; Morishita, T.; Sakai, K.; Sakai, H.; Abe, M.; Nakase, I.; Futaki, S. Bioinspired Mechanism for the Translocation of Peptide Through the Cell Membrane. Chem. Lett. 2012, 41, 1078–1080. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesarec, L.; Kralj, S.; Iglič, A. Biaxial Structures of Localized Deformations and Line-like Distortions in Effectively 2D Nematic Films. Nanomaterials 2024, 14, 246. https://doi.org/10.3390/nano14030246
Mesarec L, Kralj S, Iglič A. Biaxial Structures of Localized Deformations and Line-like Distortions in Effectively 2D Nematic Films. Nanomaterials. 2024; 14(3):246. https://doi.org/10.3390/nano14030246
Chicago/Turabian StyleMesarec, Luka, Samo Kralj, and Aleš Iglič. 2024. "Biaxial Structures of Localized Deformations and Line-like Distortions in Effectively 2D Nematic Films" Nanomaterials 14, no. 3: 246. https://doi.org/10.3390/nano14030246
APA StyleMesarec, L., Kralj, S., & Iglič, A. (2024). Biaxial Structures of Localized Deformations and Line-like Distortions in Effectively 2D Nematic Films. Nanomaterials, 14(3), 246. https://doi.org/10.3390/nano14030246