Review of Recent Developments on Using an Off-Lattice Monte Carlo Approach to Predict the Effective Thermal Conductivity of Composite Systems with Complex Structures
Abstract
:1. Introduction
2. Simulation Methods
3. Results and Discussion
3.1. Model of Three-Phase SWNT/WS2/PEEK Composites
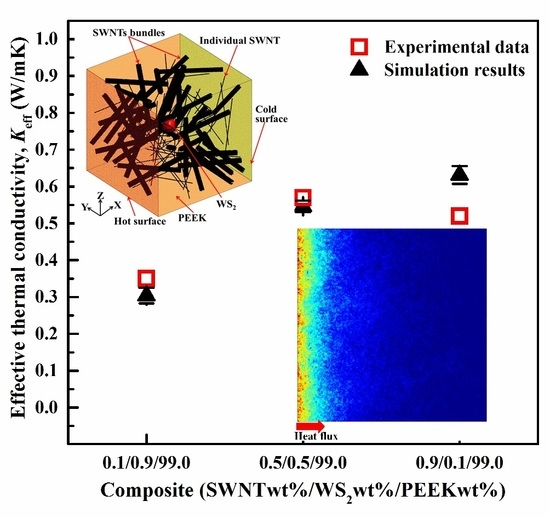
3.1.1. Validation of the Developed Off-Lattice Monte Carlo Approach
3.1.2. Effects of Interfacial Thermal Resistances on the Keff of SWNT/WS2/PEEK Composites
3.1.3. Effects of the Morphology of SWNTs on the Keff of SWNT/WS2/PEEK Composites
3.2. Model of SWNT/WS2/PEEK Composites with SWNT Bundles
3.2.1. Effects of the Morphology of SWNT Bundles on the Keff of SWNT/WS2/PEEK Composites
3.2.2. Effects of the SWNT-SWNT Thermal Resistance on the Keff of SWNT/WS2/PEEK Composites
3.3. Model of Graphene/PMMA with Complex Structure
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Thakur, V.K.; Thakur, M.K.; Raghavan, P.; Kessler, M.R. Progress in green polymer composites from lignin for multifunctional applications: A review. ACS Sustain. Chem. Eng. 2014, 2, 1072–1092. [Google Scholar] [CrossRef]
- De Volder, M.F.L.; Tawfick, S.H.; Baughman, R.H.; Hart, A.J. Carbon nanotubes: Present and future commercial applications. Science 2013, 339, 535–539. [Google Scholar] [CrossRef] [PubMed]
- Shahil, K.M.F.; Balandin, A.A. Graphene-multilayer graphene nanocomposites as highly efficient thermal interface materials. Nano Lett. 2012, 12, 861–867. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Gong, F.; Nguyen, S.T.; Duong, H.M. Advanced multifunctional graphene aerogel—Poly(methyl methacrylate) composites: Experiments and modeling. Carbon 2015, 81, 396–404. [Google Scholar] [CrossRef]
- Dai, W.; Yu, J.; Liu, Z.; Wang, Y.; Song, Y.; Lyu, J.; Bai, H.; Nishimura, K.; Jiang, N. Enhanced thermal conductivity and retained electrical insulation for polyimide composites with sic nanowires grown on graphene hybrid fillers. Compos. Part A 2015, 76, 73–81. [Google Scholar] [CrossRef]
- Yan, Z.; Nika, D.L.; Balandin, A.A. Thermal properties of graphene and few-layer graphene: Applications in electronics. Inst. Eng. Technol. 2015, 9, 4–12. [Google Scholar] [CrossRef]
- Qian, R.; Yu, J.; Wu, C.; Zhai, X.; Jiang, P. Alumina-coated graphene sheet hybrids for electrically insulating polymer composites with high thermal conductivity. RSC Adv. 2013, 3, 17373–17379. [Google Scholar] [CrossRef]
- Zhao, Y.-H.; Zhang, Y.-F.; Bai, S.-L. High thermal conductivity of flexible polymer composites due to synergistic effect of multilayer graphene flakes and graphene foam. Compos. Part A 2016, 85, 148–155. [Google Scholar] [CrossRef]
- Naffakh, M.; Diez-Pascual, A.M.; Gomez-Fatou, M.A. New hybrid nanocomposites containing carbon nanotubes, inorganic fullerene-like WS2 nanoparticles and poly(ether ether ketone) (PEEK). J. Mater. Chem. 2011, 21, 7425–7433. [Google Scholar] [CrossRef]
- Naffakh, M.; Diez-Pascual, A.M.; Marco, C.; Ellis, G. Morphology and thermal properties of novel poly(phenylene sulfide) hybrid nanocomposites based on single-walled carbon nanotubes and inorganic fullerene-like WS2 nanoparticles. J. Mater. Chem. 2012, 22, 1418–1425. [Google Scholar] [CrossRef]
- Im, H.; Kim, J. Thermal conductivity of a graphene oxide–carbon nanotube hybrid/epoxy composite. Carbon 2012, 50, 5429–5440. [Google Scholar] [CrossRef]
- Gupta, T.K.; Singh, B.P.; Mathur, R.B.; Dhakate, S.R. Multi-walled carbon nanotube-graphene-polyaniline multiphase nanocomposite with superior electromagnetic shielding effectiveness. Nanoscale 2014, 6, 842–851. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Park, J.S.; Lim, Y.-S.; Lee, C.S.; Shin, K.; Moon, H.J.; Yang, C.-M.; Lee, Y.S.; Han, J.H. Carbon hybrid fillers composed of carbon nanotubes directly grown on graphene nanoplatelets for effective thermal conductivity in epoxy composites. Nanotechnology 2013, 24. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Zhao, L. Effect of nano-fillers on the thermal conductivity of epoxy composites with micro-Al2O3 particles. Mater. Des. 2015, 66, 176–182. [Google Scholar] [CrossRef]
- Luan, V.H.; Tien, H.N.; Cuong, T.V.; Kong, B.-S.; Chung, J.S.; Kim, E.J.; Hur, S.H. Novel conductive epoxy composites composed of 2-D chemically reduced graphene and 1-D silver nanowire hybrid fillers. J. Mater. Chem. 2012, 22, 8649–8653. [Google Scholar] [CrossRef]
- Cheng, H.K.F.; Basu, T.; Sahoo, N.G.; Li, L.; Chan, S.H. Current advances in the carbon nanotube/thermotropic main-chain liquid crystalline polymer nanocomposites and their blends. Polymers 2012, 4, 889–912. [Google Scholar] [CrossRef]
- Wang, F.; Drzal, L.T.; Qin, Y.; Huang, Z. Enhancement of fracture toughness, mechanical and thermal properties of rubber/epoxy composites by incorporation of graphene nanoplatelets. Compos. Part A 2016, 87, 10–22. [Google Scholar] [CrossRef]
- Gong, F.; Bui, K.; Papavassiliou, D.V.; Duong, H.M. Thermal transport phenomena and limitations in heterogeneous polymer composites containing carbon nanotubes and inorganic nanoparticles. Carbon 2014, 78, 305–316. [Google Scholar] [CrossRef]
- Duong, H.M.; Papavassiliou, D.V.; Lee, L.L.; Mullen, K.J. Random walks in nanotube composites: Improved algorithms and the role of thermal boundary resistance. Appl. Phys. Lett. 2005, 87. [Google Scholar] [CrossRef]
- Voronov, R.S.; VanGordon, S.B.; Sikavitsas, V.I.; Papavassiliou, D.V. Efficient lagrangian scalar tracking method for reactive local mass transport simulation through porous media. Int. J. Numer. Methods Fluids 2011, 67, 501–517. [Google Scholar] [CrossRef]
- Tomadakis, M.M.; Sotirchos, S.V. Transport properties of random arrays of freely overlapping cylinders with various orientation distributions. J. Chem. Phys. 1993, 98, 616–626. [Google Scholar] [CrossRef]
- Papavassiliou, D.V. Turbulent transport from continuous sources at the wall of a channel. Int. J. Heat Mass Transf. 2002, 45, 3571–3583. [Google Scholar] [CrossRef]
- Mitrovic, B.M.; Le, P.M.; Papavassiliou, D.V. On the prandtl or schmidt number dependence of the turbulent heat or mass transfer coefficient. Chem. Eng. Sci. 2004, 59, 543–555. [Google Scholar] [CrossRef]
- Gong, F.; Duong, H.M.; Papavassiliou, D.V. Inter-carbon nanotube contact and thermal resistances in heat transport of three-phase composites. J. Phys. Chem. C 2015, 119, 7614–7620. [Google Scholar] [CrossRef]
- Einstein, A. The electrodynamics of moving bodies. Ann. Phys. 1905, 17, 891–921. [Google Scholar] [CrossRef]
- Swartz, E.T.; Pohl, R.O. Thermal-boundary resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Gong, F.; Papavassiliou, D.V.; Duong, H.M. Off-lattice monte carlo simulation of heat transfer through carbon nanotube multiphase systems taking into account thermal boundary resistances. Numer. Heat Transf. Part A 2014, 65, 1023–1043. [Google Scholar] [CrossRef]
- Duong, H.M.; Yamamoto, N.; Papavassiliou, D.V.; Maruyama, S.; Wardle, B.L. Inter-carbon nanotube contact in thermal transport of controlled-morphology polymer nanocomposites. Nanotechnology 2009, 20. [Google Scholar] [CrossRef] [PubMed]
- Gong, F.; Hongyan, Z.; Papavassiliou, D.V.; Bui, K.; Lim, C.; Duong, H.M. Mesoscopic modeling of cancer photothermal therapy using single-walled carbon nanotubes and near infrared radiation: Insights through an off-lattice monte carlo approach. Nanotechnology 2014, 25. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Diez-Pascual, A.M.; Naffakh, M.; Marco, C.; Ellis, G.; Gomez-Fatou, M.A. High-performance nanocomposites based on polyetherketones. Prog. Mater. Sci. 2012, 57, 1106–1190. [Google Scholar] [CrossRef]
- Hida, S.; Hori, T.; Shiga, T.; Elliott, J.; Shiomi, J. Thermal resistance and phonon scattering at the interface between carbon nanotube and amorphous polyethylene. Int. J. Heat Mass Transf. 2013, 67, 1024–1029. [Google Scholar] [CrossRef]
- Haggenmueller, R.; Guthy, C.; Lukes, J.R.; Fischer, J.E.; Winey, K.I. Single wall carbon nanotube/polyethylene nanocomposites: Thermal and electrical conductivity. Macromolecules 2007, 40, 2417–2421. [Google Scholar] [CrossRef]
- Jiang, W.T.; Ding, G.L.; Peng, H. Measurement and model on thermal conductivities of carbon nanotube nanorefrigerants. Int. J. Therm. Sci. 2009, 48, 1108–1115. [Google Scholar] [CrossRef]
- Nan, C.W.; Shi, Z.; Lin, Y. A simple model for thermal conductivity of carbon nanotube-based composites. Chem. Phys. Lett. 2003, 375, 666–669. [Google Scholar] [CrossRef]
- Xue, Q.Z. Model for the enective thermal conductivity of carbon nanotube composites. Nanotechnology 2006, 17, 1655–1660. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Nan, C.W.; Liu, G.; Lin, Y.H.; Li, M. Interface effect on thermal conductivity of carbon nanotube composites. Appl. Phys. Lett. 2004, 85, 3549–3551. [Google Scholar] [CrossRef]
- Han, Z.D.; Fina, A. Thermal conductivity of carbon nanotubes and their polymer nanocomposites: A review. Prog. Polym. Sci. 2011, 36, 914–944. [Google Scholar] [CrossRef]
- Shenogin, S. Role of thermal boundary resistance on the heat flow in carbon-nanotube composites. J. Appl. Phys. 2004, 95. [Google Scholar] [CrossRef]
- Konatham, D.; Striolo, A. Thermal boundary resistance at the graphene-oil interface. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
- Maruyama, S.; Igarashi, Y.; Taniguchi, Y.; Shiomi, J. Anisotropic heat transfer of single-walled carbon nanotubes. J. Therm. Sci. Technol. 2006, 1, 138–148. [Google Scholar] [CrossRef]
- Huxtable, S.T.; Cahill, D.G.; Shenogin, S.; Xue, L.P.; Ozisik, R.; Barone, P.; Usrey, M.; Strano, M.S.; Siddons, G.; Shim, M.; et al. Interfacial heat flow in carbon nanotube suspensions. Nat. Mater. 2003, 2, 731–734. [Google Scholar] [CrossRef] [PubMed]
- Shukla, N.C.; Liao, H.H.; Abiade, J.T.; Liu, F.X.; Liaw, P.K.; Huxtable, S.T. Thermal conductivity and interface thermal conductance of amorphous and crystalline Zr47Cu31Al13Ni9 alloys with a Y2O3 coating. Appl. Phys. Lett. 2009, 94. [Google Scholar] [CrossRef]
- Shenogin, S.; Bodapati, A.; Xue, L.; Ozisik, R.; Keblinski, P. Effect of chemical functionalization on thermal transport of carbon nanotube composites. Appl. Phys. Lett. 2004, 85, 2229–2231. [Google Scholar] [CrossRef]
- Clancy, T.C.; Gates, T.S. Modeling of interfacial modification effects on thermal conductivity of carbon nanotube composites. Polymer 2006, 47, 5990–5996. [Google Scholar] [CrossRef]
- Lin, S.C.; Buehler, M.J. The effect of non-covalent functionalization on the thermal conductance of graphene/organic interfaces. Nanotechnology 2013, 24. [Google Scholar] [CrossRef] [PubMed]
- Cherkasova, A.S.; Shan, J.W. Particle aspect-ratio effects on the thermal conductivity of micro- and nanoparticle suspensions. J. Heat Transf. Trans. ASME 2008, 130. [Google Scholar] [CrossRef]
- Kapadia, R.S.; Louie, B.M.; Bandaru, P.R. The influence of carbon nanotube aspect ratio on thermal conductivity enhancement in nanotube-polymer composites. J. Heat Transf.Trans. ASME 2014, 136. [Google Scholar] [CrossRef]
- Cherkasova, A.S.; Shan, J.W. Particle aspect-ratio and agglomeration-state effects on the effective thermal conductivity of aqueous suspensions of multiwalled carbon nanotubes. J. Heat Transf. Trans. ASME 2010, 132. [Google Scholar] [CrossRef]
- Kim, P.; Shi, L.; Majumdar, A.; McEuen, P.L. Thermal transport measurements of individual multiwalled nanotubes. Phys. Rev. Lett. 2001, 87. [Google Scholar] [CrossRef] [PubMed]
- Prasher, R. Thermal boundary resistance and thermal conductivity of multiwalled carbon nanotubes. Phys. Rev. B 2008, 77. [Google Scholar] [CrossRef]
- Volkov, A.N.; Zhigilei, L.V. Scaling laws and mesoscopic modeling of thermal conductivity in carbon nanotube materials. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.S.; Youn, J.R. Influence of dispersion states of carbon nanotubes on physical properties of epoxy nanocomposites. Carbon 2005, 43, 1378–1385. [Google Scholar] [CrossRef]
- Roy, A.K.; Farmer, B.L.; Varshney, V.; Sihn, S.; Lee, J.; Ganguli, S. Importance of interfaces in governing thermal transport in composite materials: Modeling and experimental perspectives. ACS Appl. Mater. Interfaces 2012, 4, 545–563. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.; Lukes, J.R. Interfacial thermal resistance between carbon nanotubes: Molecular dynamics simulations and analytical thermal modeling. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Duong, H.M.; Yamamoto, N.; Bui, K.; Papavassiliou, D.V.; Maruyama, S.; Wardle, B.L. Morphology effects on nonisotropic thermal conduction of aligned single-walled and multi-walled carbon nanotubes in polymer nanocomposites. J. Phys. Chem. C 2010, 114, 8851–8860. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Farmer, B.L. Modeling of thermal conductance at transverse CNT-CNT interfaces. J. Phys. Chem. C 2010, 114, 16223–16228. [Google Scholar] [CrossRef]
- Gharib-Zahedi, M.R.; Tafazzoli, M.; Böhm, M.C.; Alaghemandi, M. Transversal thermal transport in single-walled carbon nanotube bundles: Influence of axial stretching and intertube bonding. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Navarro, C.; Weitz, R.T.; Bittner, A.M.; Scolari, M.; Mews, A.; Burghard, M.; Kern, K. Electronic transport properties of individual chemically reduced graphene oxide sheets. Nano Lett. 2007, 7, 3499–3503. [Google Scholar] [CrossRef] [PubMed]
- Becerril, H.A.; Mao, J.; Liu, Z.; Stoltenberg, R.M.; Bao, Z.; Chen, Y. Evaluation of solution-processed reduced graphene oxide films as transparent conductors. ACS Nano 2008, 2, 463–470. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Zhang, Y.; Li, P.; Gao, C. Strong, conductive, lightweight, neat graphene aerogel fibers with aligned pores. ACS Nano 2012, 6, 7103–7113. [Google Scholar] [CrossRef] [PubMed]








© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, F.; Duong, H.M.; Papavassiliou, D.V. Review of Recent Developments on Using an Off-Lattice Monte Carlo Approach to Predict the Effective Thermal Conductivity of Composite Systems with Complex Structures. Nanomaterials 2016, 6, 142. https://doi.org/10.3390/nano6080142
Gong F, Duong HM, Papavassiliou DV. Review of Recent Developments on Using an Off-Lattice Monte Carlo Approach to Predict the Effective Thermal Conductivity of Composite Systems with Complex Structures. Nanomaterials. 2016; 6(8):142. https://doi.org/10.3390/nano6080142
Chicago/Turabian StyleGong, Feng, Hai M. Duong, and Dimitrios V. Papavassiliou. 2016. "Review of Recent Developments on Using an Off-Lattice Monte Carlo Approach to Predict the Effective Thermal Conductivity of Composite Systems with Complex Structures" Nanomaterials 6, no. 8: 142. https://doi.org/10.3390/nano6080142
APA StyleGong, F., Duong, H. M., & Papavassiliou, D. V. (2016). Review of Recent Developments on Using an Off-Lattice Monte Carlo Approach to Predict the Effective Thermal Conductivity of Composite Systems with Complex Structures. Nanomaterials, 6(8), 142. https://doi.org/10.3390/nano6080142