3D Nanoporous Anodic Alumina Structures for Sustained Drug Release
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication of NAA Structures
2.2. Characterization of NAA Structures
2.3. Drug Loading and Release
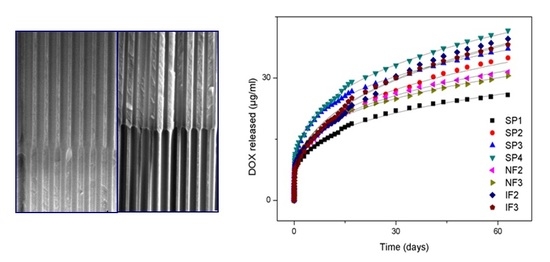
3. Results and Discussion
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Allen, T.M.; Cullis, P.R. Drug delivery systems: Entering the mainstream. Science 2004, 303, 1818–1822. [Google Scholar] [CrossRef] [PubMed]
- Losic, D.; Simovic, S. Self-ordered nanopore and nanotube platforms for drug delivery applications. Expert Opin. Drug Deliv. 2009, 6, 1363–1381. [Google Scholar] [CrossRef] [PubMed]
- Yao, F.; Weiyuan, J.K. Drug Release Kinetics and Transport Mechanisms of Nondegradable and Degradable Polymeric Delivery Systems. Expert Opin. Drug Deliv. 2011, 7, 429–444. [Google Scholar]
- Gultepe, E.; Nagesha, D.; Casse, B.D.F.; Banyal, R.; Fitchorov, T.; Karma, A.; Amiji, M.; Sridhar, S. Sustained drug release from non-eroding nanoporous templates. Small 2010, 6, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Fornell, J.; Soriano, J.; Guerrero, M.; Sirvent, J.; Ferran-Marqués, M.; Ibáñez, E.; Barrios, L.; Baró, M.D.; Suriñach, S.; Nogués, C.; et al. Biodegradable FeMnSi Sputter-Coated Macroporous Polypropylene Membranes for the Sustained Release of Drugs. Nanomaterials 2017, 7, 155. [Google Scholar] [CrossRef] [PubMed]
- Sinn Aw, M.; Kurian, M.; Losic, D. Non-eroding drug-releasing implants with ordered nanoporous and nanotubular structures: Concepts for controlling drug release. Biomater. Sci. 2014, 2, 10–34. [Google Scholar] [CrossRef]
- McInnes, S.J.; Irani, Y.; Williams, K.A.; Voelcker, N.H. Controlled drug delivery from composites of nanostructured porous silicon and poly (l-lactide) Research Article. Nanomedicine 2012, 7, 995–1016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costa, P.; Sousa Lobo, J.M. Modeling and comparison of dissolution profiles. Eur. J. Pharm. Sci. 2001, 13, 123–133. [Google Scholar] [CrossRef]
- Singhvi, G.; Singh, M. In Vitro drug release characterization models. Int. J. Pharm. Stud. Res. 2011, II, 77–84. [Google Scholar]
- Kikuchi, A.; Okano, T. Pulsatile drug release control using hydrogels. Adv. Drug Deliv. Rev. 2002, 54, 53–77. [Google Scholar] [CrossRef]
- Lin, C.C.; Metters, A.T. Hydrogels in controlled release formulations: Network design and mathematical modeling. Adv. Drug Deliv. Rev. 2006, 58, 1379–1408. [Google Scholar] [CrossRef] [PubMed]
- Carregal-Romero, S.; Guardia, P.; Yu, X.; Hartmann, R.; Pellegrino, T.; Parak, W.J. Magnetically triggered release of molecular cargo from iron oxide nanoparticle loaded microcapsules. Nanoscale 2015, 7, 570–576. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Xia, J.; Zhao, Q.; Liu, L.; Zhang, Z. Functional graphene oxide as a nanocarrier for controlled loading and targeted delivery of mixed anticancer drugs. Small 2010, 6, 537–544. [Google Scholar] [CrossRef] [PubMed]
- Alba, M.; Delalat, B.; Formentín, P.; Rogers, M.L.; Marsal, L.F.; Voelcker, N.H. Silica Nanopills for Targeted Anticancer Drug Delivery. Small 2015, 11, 4626–4631. [Google Scholar] [CrossRef] [PubMed]
- Romero, V.; Vega, V.; García, J.; Prida, V.; Hernando, B.; Benavente, J. Effect of Porosity and Concentration Polarization on Electrolyte Diffusive Transport Parameters through Ceramic Membranes with Similar Nanopore Size. Nanomaterials 2014, 4, 700–711. [Google Scholar] [CrossRef] [PubMed]
- Kumeria, T.; Santos, A.; Rahman, M.M.; Ferré-Borrull, J.; Marsal, L.F.; Losic, D. Advanced Structural Engineering of Nanoporous Photonic Structures: Tailoring Nanopore Architecture to Enhance Sensing Properties. ACS Photonics 2014, 1, 1298–1306. [Google Scholar] [CrossRef]
- Santos, A.; Formentín, P.; Pallarès, J.; Ferré-Borrull, J.; Marsal, L.F. Structural engineering of nanoporous anodic alumina funnels with high aspect ratio. J. Electroanal. Chem. 2011, 655, 73–78. [Google Scholar] [CrossRef]
- Santos, A.; Kumeria, T.; Wang, Y.; Losic, D. Insitu monitored engineering of inverted nanoporous anodic alumina funnels: On the precise generation of 3D optical nanostructures. Nanoscale 2014, 6, 9991–9999. [Google Scholar] [CrossRef] [PubMed]
- Hanawa, T. Materials for metallic stents. J. Artif. Organs 2009, 12, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Swan, E.E.L.; Popat, K.C.; Grimes, C.A.; Desai, T.A. Fabrication and evaluation of nanoporous alumina membranes for osteoblast culture. J. Biomed. Mater. Res. Part A 2005, 72, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Osmanbeyoglu, H.U.; Hur, T.B.; Kim, H.K. Thin alumina nanoporous membranes for similar size biomolecule separation. J. Membr. Sci. 2009, 343, 1–6. [Google Scholar] [CrossRef]
- Porta-i-Batalla, M.; Eckstein, C.; Xifré-Pérez, E.; Formentín, P.; Ferré-Borrull, J.; Marsal, L.F. Sustained, Controlled and Stimuli-Responsive Drug Release Systems Based on Nanoporous Anodic Alumina with Layer-by-Layer Polyelectrolyte. Nanoscale Res. Lett. 2016, 11, 372. [Google Scholar] [CrossRef] [PubMed]
- Jeon, G.; Yang, S.Y.; Kim, J.K. Functional nanoporous membranes for drug delivery. J. Mater. Chem. 2012, 22, 14814. [Google Scholar] [CrossRef]
- Xifre-Perez, E.; Guaita-Esteruelas, S.; Baranowska, M.; Pallares, J.; Masana, L.; Marsal, L.F. In Vitro Biocompatibility of Surface-Modified Porous Alumina Particles for HepG2 Tumor Cells: Toward Early Diagnosis and Targeted Treatment. ACS Appl. Mater. Interfaces 2015, 7, 18600–18608. [Google Scholar] [CrossRef] [PubMed]
- Ribes, À.; Xifré-Pérez, E.; Aznar, E.; Sancenón, F.; Pardo, T.; Marsal, L.F.; Martínez-Máñez, R. Molecular gated nanoporous anodic alumina for the detection of cocaine. Sci. Rep. 2016, 6, 38649. [Google Scholar] [CrossRef] [PubMed]
- Pla, L.; Xifre-Perez, E.; Ribes, A.; Aznar, E.; Marcos, M.D.; Marsal, L.F.; Martínez-Mañez, R.; Sancenon, F. A Mycoplasma Genomic DNA Probe using Gated Nanoporous Anodic Alumina. Chempluschem 2017, 82, 337–341. [Google Scholar] [CrossRef]
- Vázquez, M.I.; Romero, V.; Vega, V.; García, J.; Prida, V.M.; Hernando, B.; Benavente, J. Morphological, Chemical Surface, and Diffusive Transport Characterizations of a Nanoporous Alumina Membrane. Nanomaterials 2015, 5, 2192–2202. [Google Scholar] [CrossRef] [PubMed]
- Santos, A.; Ferré-Borrull, J.; Pallarès, J.; Marsal, L.F. Hierarchical nanoporous anodic alumina templates by asymmetric two-step anodization. Phys. Status Solidi Appl. Mater. Sci. 2011, 208, 668–674. [Google Scholar] [CrossRef]
- Marsal, L.F.; Vojkuvka, L.; Formentin, P.; Pallarés, J.; Ferré-Borrull, J. Fabrication and optical characterization of nanoporous alumina films annealed at different temperatures. Opt. Mater. 2009, 31, 860–864. [Google Scholar] [CrossRef]
- Santos, A.; Vojkuvka, L.; Alba, M.; Balderrama, V.S.; Ferre-Borrull, J.; Pallares, J.; Marsal, L.F. Understanding and morphology control of pore modulations in nanoporous anodic alumina by discontinuous anodization. Phys. Status Solidi Appl. Mater. Sci. 2012, 209, 2045–2048. [Google Scholar] [CrossRef]
- Mardilovich, P.P.; Govyadinov, A.N.; Mukhurov, N.I.; Rzhevskii, A.M.; Paterson, R. New and Modified Anodic Alumina Membranes. 1. Thermotreatment of Anodic Alumina Membranes. J. Memb. Sci. 1995, 98, 131–142. [Google Scholar] [CrossRef]
- Losic, D.; Santos, A. Nanoporous Alumina : Fabrication, Structure, Properties and Applications; Springer: Adelaide, Australia, 2015. [Google Scholar]
- Han, H.; Park, S.J.; Jang, J.S.; Ryu, H.; Kim, K.J.; Baik, S.; Lee, W. In situ determination of the pore opening point during wet-chemical etching of the barrier layer of porous anodic aluminum oxide: Nonuniform Impurity Distribution in Anodic Oxide. ACS Appl. Mater. Interfaces 2013, 5, 3441–3448. [Google Scholar] [CrossRef] [PubMed]
- Iskakov, R.M.; Kikuchi, A.; Okano, T. Time-programmed pulsatile release of dextran from calcium-alginate gel beads coated with carboxy-n-propylacrylamide copolymers. J. Control. Release 2002, 80, 57–68. [Google Scholar] [CrossRef]
- Aukunuru, J.V.; Sunkara, G.; Ayalasomayajula, S.P.; Deruiter, J.; Clark, R.C.; Kompella, U.B. A biodegradable injectable implant sustains systemic and ocular delivery of an aldose reductase inhibitor and ameliorates biochemical changes in a galactose-fed rat model for diabetic complications. Pharm. Res. 2002, 19, 278–285. [Google Scholar] [CrossRef] [PubMed]
- Horcajada, P.; Chalati, T.; Serre, C.; Gillet, B.; Sebrie, C.; Baati, T.; Eubank, J.F.; Heurtaux, D.; Clayette, P.; Kreuz, C.; et al. Porous metal–organic-framework nanoscale carriers as a potential platform for drug delivery and imaging. Nat. Mater. 2010, 9, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Vallet-Regí, M.; Balas, F.; Arcos, D. Mesoporous materials for drug delivery. Angew. Chem. 2007, 46, 7548–7558. [Google Scholar] [CrossRef] [PubMed]
- Shoaib, M.H.; Tazeen, J.; Merchant, H.A.; Yousuf, R.I. Evaluation of Drug Release Kinetics From Ibuprofen Matrix Tablets Using Hpmc. Pak. J. Pharm. Sci. 2006, 19, 119–124. [Google Scholar] [PubMed]
- Higuchi, T. Rate of release of medicaments from ointment bases containing drugs in suspension. J. Pharm. Sci. 1961, 50, 874–875. [Google Scholar] [CrossRef] [PubMed]
- Higuchi, T. Mechanism of Sustained-Action Medication. Theoretical Analysis of Rate of Release of Solid Drugs Dispersed in Solid Matrices. J. Pharm. Sci. 1963, 52, 1145–1149. [Google Scholar] [CrossRef] [PubMed]
- Brophy, M.R.; Deasy, P.B. Application of the Higuchi model for drug release from dispersed matrices to particles of general shape. Int. J. Pharm. 1987, 37, 41–47. [Google Scholar] [CrossRef]
- Suvakanta, D.; Murthy, P.N.; Nath, L.; Prasanta, C. Kinetic Modeling on Drug Release from Controlled Drug Delivery Systems. Pol. Pharm. Soc. 2010, 67, 217–223. [Google Scholar]











| Sample Name | Release Constant (K) | Intercept (M0) |
|---|---|---|
| SP1 | 0.24 ± 0.02 | 2.34 ± 0.26 |
| SP2 | 0.30 ± 0.02 | 2.75 ± 0.29 |
| SP3 | 0.35 ± 0.02 | 3.38 ± 0.29 |
| SP4 | 0.44 ± 0.02 | 2.01 ± 0.43 |
| NF2 | 0.28 ± 0.01 | 2.45 ± 0.21 |
| NF3 | 0.31 ± 0.01 | 2.31 ± 0.25 |
| IF2 | 0.32 ± 0.01 | 2.28 ± 0.25 |
| IF3 | 0.27 ± 0.01 | 1.89 ± 0.20 |
| Sample Name | Mt0 (μg/mL) | n | Release Rate |
|---|---|---|---|
| SP1 | 8.43 ± 0.14 | 0.27 ± 0.01 | 2.31 |
| SP2 | 9.93 ± 0.21 | 0.30 ± 0.001 | 2.94 |
| SP3 | 12.49 ± 0.17 | 0.26 ± 0.00 | 3.27 |
| SP4 | 12.55 ± 0.22 | 0.28 ± 0.01 | 3.60 |
| NF2 | 9.70 ± 0.16 | 0.29 ± 0.00 | 2.78 |
| NF3 | 10.14 ± 0.15 | 0.27 ± 0.00 | 2.69 |
| IF2 | 9.00 ± 0.33 | 0.35 ± 0.01 | 3.16 |
| IF3 | 8.91 ± 0.18 | 0.35 ± 0.01 | 3.13 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porta-i-Batalla, M.; Xifré-Pérez, E.; Eckstein, C.; Ferré-Borrull, J.; Marsal, L.F. 3D Nanoporous Anodic Alumina Structures for Sustained Drug Release. Nanomaterials 2017, 7, 227. https://doi.org/10.3390/nano7080227
Porta-i-Batalla M, Xifré-Pérez E, Eckstein C, Ferré-Borrull J, Marsal LF. 3D Nanoporous Anodic Alumina Structures for Sustained Drug Release. Nanomaterials. 2017; 7(8):227. https://doi.org/10.3390/nano7080227
Chicago/Turabian StylePorta-i-Batalla, Maria, Elisabet Xifré-Pérez, Chris Eckstein, Josep Ferré-Borrull, and Lluis F. Marsal. 2017. "3D Nanoporous Anodic Alumina Structures for Sustained Drug Release" Nanomaterials 7, no. 8: 227. https://doi.org/10.3390/nano7080227
APA StylePorta-i-Batalla, M., Xifré-Pérez, E., Eckstein, C., Ferré-Borrull, J., & Marsal, L. F. (2017). 3D Nanoporous Anodic Alumina Structures for Sustained Drug Release. Nanomaterials, 7(8), 227. https://doi.org/10.3390/nano7080227