Long-Term Mechanical Behavior of Nano Silica Sol Grouting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation and Curing Conditions
2.3. Testing Methods
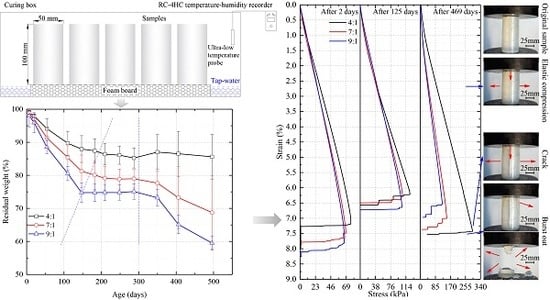
3. Results
4. Discussion
4.1. Weight- and Geometric Parameter-Time Law
4.2. Strength- and Secant Modulus-Time Law and Micro-Mechanism
4.3. Plastic Strength-Time Law
5. Conclusions
- (1)
- The temperature and humidity fluctuate over both long and short periods. As the dosage of catalyst in the grout mix is decreased, the curves showing the changes in sample weight and sample width, height, and volume over time can be divided into three stages, a shrinkage stage, a stable stage, and a second shrinkage stage. Higher amounts of catalyst improve the stability of the samples and reduce moisture loss. Temperature rise is also a driving force for moisture loss.
- (2)
- The uniaxial compressive stress-strain curves all show that the samples are elastoplastic. The deformation can be divided into four phases, a compaction phase, an elastic phase, a plastic phase, and a post-peak stress phase. The curves for the uniaxial compression strength and the secant modulus can be divided into an ascending stage, a descending stage, and a second ascending stage. Peak strain for the samples changed little with curing time. The PASED-time curves are W-shaped and are essentially unaffected by the amount of catalyst prior to 400 days. After 400 days, higher catalyst ratios increase the PASED values significantly. Sample brittleness increases with time and in the later stages of the experiment, the brittleness index increases with higher catalyst dosages.
- (3)
- Plastic strength-time curves for samples with different proportions of catalyst exhibit allometric scaling. A consistent effect of catalyst dosage on plastic strength is not apparent prior to 400 days of curing but after 400 days, it is clear that when the grout mix contains less catalyst, the plastic strength of the grout is greater.
- (4)
- The surfaces of samples are smooth and compact at different ages, substantially unchanging. The crystal structure of samples are basically unchanged. Ultrasonic velocity-time curves for samples are similar to UCS curves. These indicate that the curing conditions mainly affect the compactness, and then affect the strength.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Morris, C.; Anderson, M.; Stroud, R.; Merzbacher, C.; Rolison, D. Silica sol as a nanoglue: Flexible synthesis of composite aerogels. Science 1999, 284, 622–624. [Google Scholar] [CrossRef] [PubMed]
- Pan, D.; Zhang, N.; Han, C.; Yang, S.; Zhang, C.; Xie, Z. Experimental Study of Imbibition Characteristics of Silica Sol in Coal-Measure Mudstone Matrix. Appl. Sci. 2017, 7, 300. [Google Scholar] [CrossRef]
- Jurinak, J.; Summers, L. Oilfield Applications of Colloidal Silica Gel. SPE Prod. Eng. 1991, 6, 406–412. [Google Scholar] [CrossRef]
- Persoff, P.; Finsterle, S.; Moridis, G.; Apps, J.; Pruess, K.; Muller, S. Injectable Barriers for Waste Isolation; Technical Report; Lawrence Berkeley Lab: Berkeley, CA, USA, 1995; pp. 1–11. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, H.; Fu, D. Shield Tunnel; China Communications Press: Beijing, China, 2004; pp. 260–261. ISBN 7-114-05174-3. [Google Scholar]
- Butrón, C.; Axelsson, M.; Gustafson, G. Silica sol for rock grouting: Laboratory testing of strength, fracture behaviour and hydraulic conductivity. Tunn. Undergr. Space Technol. 2009, 24, 603–607. [Google Scholar] [CrossRef]
- Axelsson, M. Mechanical tests on a new non-cementitious grout, silica sol: A laboratory study of the material characteristics. Tunn. Undergr. Space Technol. 2006, 21, 554–560. [Google Scholar] [CrossRef]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock—New methods for calculation of penetration length, Part I. Tunn. Undergr. Space Technol. 2008, 23, 1–8. [Google Scholar] [CrossRef]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock—New design criteria tested in the field, Part II. Tunn. Undergr. Space Technol. 2008, 23, 9–17. [Google Scholar] [CrossRef]
- Butrón, C.; Gustafson, G.; Fransson, Å.; Funehag, J. Drip sealing of tunnels in hard rock: A new concept for the design and evaluation of permeation grouting. Tunn. Undergr. Space Technol. 2010, 25, 114–121. [Google Scholar] [CrossRef]
- McCartney, J.; Nogueira, C.; Homes, D.; Zornberg, J. Formation of Secondary Containment Systems Using Permeation of Colloidal Silica. J. Environ. Eng. 2011, 137, 444–453. [Google Scholar] [CrossRef]
- Hamderi, M.; Gallagher, P.; Lin, Y. Numerical Model for Colloidal Silica Injected Column Tests. Vadose Zone J. 2014, 13, 138–143. [Google Scholar] [CrossRef]
- Wang, Q.; Li, H.; Zhu, N. Research on water plugging with nanoscale grouting material and high-property concrete in slope shaft. Coal Min. Technol. 2013, 18, 97–98. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, F. Grouting Construction and Effect Detection in Civil Engineering; Tongji University Press: Shanghai, China, 1998; p. 78. ISBN 7-5608-1763-7. [Google Scholar]
- Zhao, J.; Yao, Y. Research on periodically change of airflow temperature in coal mine. China Coal 2012, 38, 98–101. [Google Scholar] [CrossRef]
- Qin, Y.; Song, H.; Wu, J.; Dong, Z. Numerical analysis of temperature field of surrounding rock under periodic boundary using Finite Volume Method. J. China Coal Soc. 2015, 40, 1541–1549. [Google Scholar] [CrossRef]
- Pan, D.; Zhang, N.; Xie, Z.; Feng, X.; Kong, Y. Laboratory Testing of Silica Sol Grout in Coal Measure Mudstones. Materials 2016, 9, 940. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Liu, B.; Qiao, S.; Yang, X.; Wu, G. Experimental research on new grouting materials of acidic water glass-calcium carbonate. Rock Soil Mech. 2010, 31, 2829–2834. [Google Scholar] [CrossRef]












| Properties | Silica Sol | Catalyst |
|---|---|---|
| Viscosity | ~10 mPa·s | ~1 mPa·s |
| Density | 1.1 kg/L | 1.07 kg/L |
| pH | 10 | 7 |
| Concentration (% by weight) | SiO2 15% | NaCl 10% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, D.; Zhang, N.; Zhang, C.; Qian, D.; Han, C.; Yang, S. Long-Term Mechanical Behavior of Nano Silica Sol Grouting. Nanomaterials 2018, 8, 46. https://doi.org/10.3390/nano8010046
Pan D, Zhang N, Zhang C, Qian D, Han C, Yang S. Long-Term Mechanical Behavior of Nano Silica Sol Grouting. Nanomaterials. 2018; 8(1):46. https://doi.org/10.3390/nano8010046
Chicago/Turabian StylePan, Dongjiang, Nong Zhang, Chenghao Zhang, Deyu Qian, Changliang Han, and Sen Yang. 2018. "Long-Term Mechanical Behavior of Nano Silica Sol Grouting" Nanomaterials 8, no. 1: 46. https://doi.org/10.3390/nano8010046
APA StylePan, D., Zhang, N., Zhang, C., Qian, D., Han, C., & Yang, S. (2018). Long-Term Mechanical Behavior of Nano Silica Sol Grouting. Nanomaterials, 8(1), 46. https://doi.org/10.3390/nano8010046