Tunable Electronic and Topological Properties of Germanene by Functional Group Modification
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
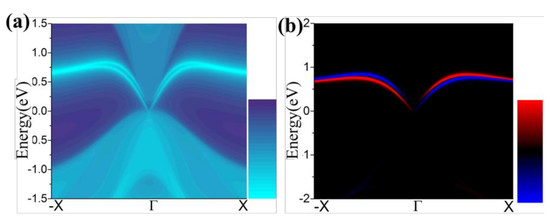
3.1. Monolayer Germanene
3.2. Functionalized Monolayer Germanene
3.3. Topological Properties
3.4. Bilayer of Functionalized Germanene
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Doubonos, S.V.; Firsov, A.A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Katsnelson, M.I.; Novoselov, K.S.; Geim, A.K. Klein paradox in graphene. Nat. Phys. 2006, 2, 620–625. [Google Scholar] [CrossRef] [Green Version]
- Tang, Q.; Zhou, Z. Graphene-Analogous Low-Dimensional Materials. Prog. Mater. Sci. 2013, 58, 1244–1315. [Google Scholar] [CrossRef]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb Carbon: A Review of Graphene. Chem. Rev. 2010, 110, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Guzmán-Verri, G.G.; Voon, L.C.L.Y. Electronic structure of silicon-based nanostructures. Phys. Rev. B 2011, 76, 12825–12834. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Kady, M.; Strong, V.; Dubin, S.; Kaner, R.B. Laser scribing of high-performance and flexible graphene-based. Science 2012, 335, 1326. [Google Scholar] [CrossRef] [PubMed]
- Pei, S.; Zhao, J.; Du, J.; Ren, W.; Cheng, H.M. Direct reduction of graphene oxide films into highly conductive and flexible graphene films by hydrohalic acids. Carbon 2010, 48, 4466–4474. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, H.; Lu, G.; Li, C.; Shi, G. Flexible Graphene Films via the Filtration of Water-Soluble Noncovalent Functionalized Graphene Sheets. J. Am. Chem. Soc. 2008, 130, 5856. [Google Scholar] [CrossRef] [PubMed]
- Gugliuzza, A.; Politano, A.; Drioli, E. The advent of graphene and other two-dimensional materials in membrane science and technology. Curr. Opin. Chem. Eng. 2017, 16, 78–85. [Google Scholar] [CrossRef]
- Politano, A.; Vitiello, M.S.; Viti, L.; Boukhvalov, D.W.; Chiarello, G. The role of surface chemical reactivity in the stability of electronic nanodevices based on two-dimensional materials “beyond graphene” and topological insulators. FlatChem 2016, 1, 60–64. [Google Scholar] [CrossRef]
- Putz, M.V.; Ori, O. Bondonic Characterization of Extended Nanosystems: Application to Graphene’s Nanoribbons. Chem. Phys. Lett. 2012, 548, 95–100. [Google Scholar] [CrossRef]
- Putz, M.V.; Ori, O. Bondonic effects in group-IV honeycomb nanoribbons with Stone-Wales topological defects. Molecules 2014, 19, 4157–4188. [Google Scholar] [CrossRef] [PubMed]
- Putz, M.V.; Ori, O. Predicting bondons by Goldstone mechanism with chemical topological indices. Int. J. Quantum. Chem. 2015, 115, 137–143. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.L.; Zhang, S.C. Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [PubMed]
- Du, L.; Knez, I.; Sullivan, G.; Du, R.R. Robust Helical Edge Transport in Gated InAs/GaSb Bilayers. Phys. Rev. Lett. 2015, 114, 096802. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Hughes, T.L.; Qi, X.L.; Wang, K.; Zhang, S.C. Quantum Spin Hall Effect in Inverted Type-II Semiconductors. Phys. Rev. Lett. 2008, 100, 236601. [Google Scholar] [CrossRef] [PubMed]
- Miller, D.L.; Kubista, K.D.; Rutter, G.M.; Ruan, M.; de Heer, W.A.; First, P.N.; Stroscio, J.A. Structural analysis of multilayer graphene via atomic moiré interferometry. Phys. Rev. B 2010, 81, 125427. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, C.; Ji, W.; Ren, M.; Li, F.; Yuan, M. First-principles Prediction on Siliene-based heterobilayers as a promising candidate for FET. Mater. Chem. Phys. 2015, 156, 89–94. [Google Scholar] [CrossRef]
- Zhang, R.W.; Zhang, C.W.; Ji, W.X.; Li, P.; Wang, P.J.; Li, S.S.; Yan, S.S. Silicon-based chalcogenide: Unexpected quantum spin Hall insulator with sizable band gap. Appl. Phys. Lett. 2016, 109, 182109. [Google Scholar] [CrossRef]
- Wang, Y.P.; Zhang, C.W.; Ji, W.X.; Li, P.; Wang, P.J.; Yan, S.S. Large-gap quantum spin Hall state in functionalized dumbbell stanene. Appl. Phys. Lett. 2016, 108, 073104. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, C.W.; Ji, W.X.; Zhang, R.W.; Li, S.S.; Yan, S.S.; Zhang, B.M.; Li, P.; Wang, P.J. Unexpected Giant-Gap Quantum Spin Hall Insulator in Chemically Decorated Plumbene Monolayer. Sci. Rep. 2016, 6, 20152. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.W.; Zhang, C.W.; Ji, W.X.; Li, S.S.; Li, P.; Wang, P.J. Room Temperature Quantum Spin Hall Insulator in Ethynyl-Derivative Functionalized Stanene Films. Sci. Rep. 2016, 6, 18879. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.W.; Ji, W.X.; Zhang, C.W.; Li, S.S.; Li, P.; Wang, P.J. New family of room temperature quantum spin Hall insulators in two-dimensional germanene films. J. Mater. Chem. C 2016, 4, 2088–2094. [Google Scholar] [CrossRef]
- Zhang, R.W.; Zhang, C.W.; Ji, W.X.; Li, S.S.; Hu, S.J.; Yan, S.S.; Li, P.; Wang, P.J.; Li, F. Ethynyl-functionalized stanene film: A promising candidate as large-gap quantum spin Hall insulator. New J. Phys. 2015, 17, 083036. [Google Scholar] [CrossRef]
- Vogt, P.; De, P.P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Silicene: Compelling experimental evidence for graphenelike two-dimensional silicon. Phys. Rev. Lett. 2012, 108, 489–492. [Google Scholar] [CrossRef] [PubMed]
- Cahangirov, S.; Topsakal, M.; Akturk, E.; Sahin, H.; Ciraci, S. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 2009, 102, 236804. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. Giant nonlocality near the dirac point in graphene. Nat. Mater. 2007, 6, 183. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, L.; Liu, Q.; Li, H.; Yu, D.; Mei, W.; Shi, J.; Gao, Z.; Lu, J. Sub-10 nm Gate Length Graphene Transistors: Operating at Terahertz Frequencies with Current Saturation. Sci. Rep. 2013, 3, 1314. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.W.; Yan, S.S. First-principles Study of Ferromagnetism in Two-Dimensional Silicene with Hydrogenation. J. Phys. Chem. C 2012, 116, 4163. [Google Scholar] [CrossRef]
- Voon, L.C.L.Y.; Sandberg, E.; Aga, R.S.; Farajian, A.A. Hydrogen compounds of group-IV nanosheets. Appl. Phys. Lett. 2010, 97, 163114. [Google Scholar] [CrossRef]
- Drummond, N.D. Electrically tunable band gap in silicone. Phys. Rev. B Condens. Matter 2011, 85, 872–878. [Google Scholar]
- Bianco, E.; Butler, S.; Jiang, S.; Restrepo, O.D.; Windl, W. Stability and exfoliation of germanae: A germanium grapheme analogue. ACS. Nano 2013, 7, 4414. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.W.; Zhang, C.W.; Li, S.S.; Ji, W.X.; Wang, P.J. Tunable electronic properties in the van der waals heterostructure of germanene/germanene. Phys. Chem. Chem. Phys. 2015, 17, 12194–12198. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.W.; Zhang, C.W.; Ji, W.X.; Yan, S.S. Silicane as an Inert Substrate of Silicene: A Promising Candidate for FET. J. Phys. Chem. C 2014, 118, 25278–25283. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y. Electronic structures of silicene fluoride and hydride. Appl. Phys. Lett. 2012, 100, 083102. [Google Scholar] [CrossRef]
- Houssa, M.; Van den Broek, B.; Scalise, E.; Pourtois, G.; Afanas’ev, V.V.; Stesmans, A. An electric field tunable energy band gap at silicene/(0001) ZnS interfaces. Phys. Chem. Chem. Phys. 2013, 15, 3702–3705. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E. Erratum: Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Erratum: Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotential to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Grimme, S.J. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Mostofi, A.A.; Yates, J.R.; Lee, Y.S.; Souza, I.; Vanderbilt, D.; Marzari, N. wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 2008, 178, 685. [Google Scholar] [CrossRef]
- Kaloni, T.P.; Schwingenschlögl, U. Stability of germanene under tensile strain. Chem. Phys. Lett. 2013, 583, 137–140. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Topological insulators with inversion symmetry. Phys. Rev. B 2007, 76, 045302. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological Insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological Insulators and Superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Li, Y.; Li, F.; Chen, Z. Graphane/fluorographene bilayer: Considerable C-H···F-C hydrogen bonding and effective band structure engineering. J. Am. Chem. Soc. 2012, 134, 11269–11275. [Google Scholar] [CrossRef] [PubMed]
- Denis, P.A. Stacked Functionalized silicone: A powerful system to adjust the electronic structure of silicone. Phys. Chem. Chem. Phys. 2015, 17, 5393–5402. [Google Scholar] [CrossRef] [PubMed]









| a (Å) | b (Å) | Ge–X/Ge–X’ (Å) | Ge–Ge (Å) | Ef (eV) | Gap (eV) | |
|---|---|---|---|---|---|---|
| Ge | 4.06 | 4.06 | \ | 2.44 | \ | 0 |
| GeH | 4.09 | 4.09 | 1.56 | 2.46 | −2.61 | 0.98 |
| GeCH3 | 4.12 | 4.12 | 2.01 | 2.50 | −4.96 | 0.78 |
| GeOH | 4.23 | 4.23 | 1.85 | 2.49 | −3.16 | 0.21 |
| GeF | 4.34 | 4.34 | 1.79 | 2.56 | −4.25 | 0.15 |
| H–Ge–CH3 | 4.10 | 4.10 | 2.01/1.56 | 2.49 | −3.82 | 0.86 |
| H–Ge–OH | 4.12 | 4.12 | 1.84/1.57 | 2.47 | −2.92 | 0.50 |
| H–Ge–F | 4.16 | 4.16 | 1.78/1.57 | 2.45 | −3.93 | 0.49 |
| CH3–Ge–OH | 4.13 | 4.15 | 2.02/1.84 | 2.51 | −4.06 | 0.44 |
| CH3–Ge–F | 4.18 | 4.18 | 2.02/1.79 | 2.51 | −4.60 | 0.41 |
| OH–Ge–F | 4.33 | 4.32 | 1.85/1.79 | 2.51 | −3.68 | 0.41 |
| Layer1/Layer2 | a (Å) | b (Å) | Interlayer Interaction (eV) | Gap (eV) |
|---|---|---|---|---|
| H–Ge–H/H–Ge–H | 4.09 | 4.09 | 0.013 | 0.96 |
| H–Ge–CH3/CH3–Ge–H | 4.10 | 4.10 | 0.030 | 0.86 |
| CH3–Ge–CH3/CH3–Ge–CH3 | 4.12 | 4.12 | 0.011 | 0.77 |
| H–Ge–F/F–Ge–H | 4.17 | 4.17 | 0.044 | 0.45 |
| H–Ge–HO/OH–Ge–H | 4.15 | 4.15 | 0.109 | 0.32 |
| H–Ge–H/OH–Ge–H | 4.11 | 4.11 | 0.002 | 0.48 |
| H–Ge–H/CH3-Ge-H | 4.09 | 4.10 | 0.013 | 0.18 |
| H–Ge–HO/F–Ge–H | 4.18 | 4.0 | 0.042 | 0.15 |
| H–Ge–H/F–Ge–H | 4.13 | 4.15 | 0.023 | metal |
| H–Ge–H/F–Ge–F | 4.20 | 4.17 | 0.034 | metal |
| H–Ge–F/CH3–Ge–H | 4.15 | 4.17 | 0.066 | metal |
| H–Ge–HO/CH3–Ge–H | 4.11 | 4.12 | 0.021 | metal |
| HO–Ge–H/F–Ge–H | 4.17 | 4.17 | 0.052 | metal |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, C.-C.; Zhang, S.-F.; Ji, W.-X.; Zhang, C.-W.; Li, P.; Wang, P.-J. Tunable Electronic and Topological Properties of Germanene by Functional Group Modification. Nanomaterials 2018, 8, 145. https://doi.org/10.3390/nano8030145
Ren C-C, Zhang S-F, Ji W-X, Zhang C-W, Li P, Wang P-J. Tunable Electronic and Topological Properties of Germanene by Functional Group Modification. Nanomaterials. 2018; 8(3):145. https://doi.org/10.3390/nano8030145
Chicago/Turabian StyleRen, Ceng-Ceng, Shu-Feng Zhang, Wei-Xiao Ji, Chang-Wen Zhang, Ping Li, and Pei-Ji Wang. 2018. "Tunable Electronic and Topological Properties of Germanene by Functional Group Modification" Nanomaterials 8, no. 3: 145. https://doi.org/10.3390/nano8030145
APA StyleRen, C. -C., Zhang, S. -F., Ji, W. -X., Zhang, C. -W., Li, P., & Wang, P. -J. (2018). Tunable Electronic and Topological Properties of Germanene by Functional Group Modification. Nanomaterials, 8(3), 145. https://doi.org/10.3390/nano8030145