Complex Magnetization Harmonics of Polydispersive Magnetic Nanoclusters
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
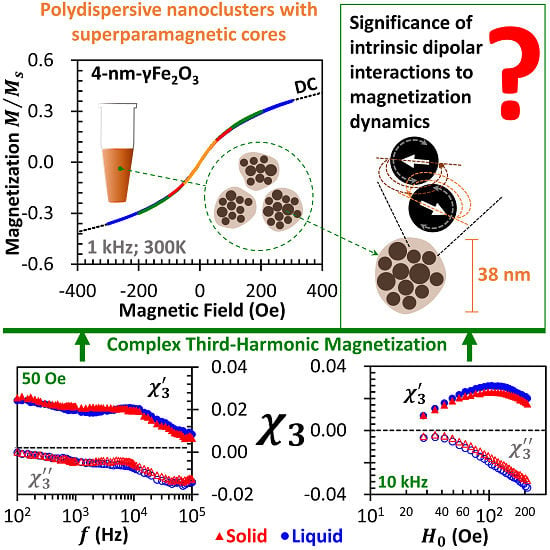
3.1. Magnetism of CMEAD-γFe2O3
3.2. Frequency and Field Dependences of Complex Third-Harmonic Magnetization
3.2.1. Spectra of Third-Harmonic Susceptibility
3.2.2. Field-Dependent Third-Harmonic Susceptibility
3.3. Damping Effect on Moment Dynamics
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Pankhurst, Q.A.; Thanh, N.T.K.; Jones, S.K.; Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224001. [Google Scholar] [CrossRef]
- Yoo, D.; Lee, J.-H.; Shin, T.-H.; Cheon, J. Theranostic magnetic nanoparticles. Acc. Chem. Res. 2011, 44, 863–874. [Google Scholar] [CrossRef] [PubMed]
- Bean, C.P.; Livingston, J.D. Superparamagnetism. J. Appl. Phys. 1959, 30, S120. [Google Scholar] [CrossRef]
- Kodama, R.H. Magnetic nanoparticles. J. Magn. Magn. Mater. 1999, 200, 359–372. [Google Scholar] [CrossRef]
- Coffey, W.T.; Cregg, P.J.; Kalmykov, Y.U.P. On the theory of Debye and Néel relaxation of single domain ferromagnetic particles. In Advances in Chemical Physics; Prigogine, I., Rice, S.A., Eds.; John Wiley & Sons Inc.: New York City, NY, USA, 2007; Volume 83, pp. 263–464. ISBN 9780471540182. [Google Scholar]
- Coffey, W.T.; Kalmykov, Y.P. Thermal fluctuations of magnetic nanoparticles: Fifty years after Brown. J. Appl. Phys. 2012, 112, 121301. [Google Scholar] [CrossRef] [Green Version]
- Mamiya, H.; Jeyadevan, B. Hyperthermic effects of dissipative structures of magnetic nanoparticles in large alternating magnetic fields. Sci. Rep. 2011, 1, 157. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.A.; Reeves, D.B.; Ferguson, R.M.; Weaver, J.B.; Krishnan, K.M. Mixed Brownian alignment and Néel rotations in superparamagnetic iron oxide nanoparticle suspensions driven by an ac field. Phys. Rev. B 2015, 92, 094438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Périgo, E.A.; Hemery, G.; Sandre, O.; Ortega, D.; Garaio, E.; Plazaola, F.; Teran, F.J. Fundamentals and advances in magnetic hyperthermia. Appl. Phys. Rev. 2015, 2, 041302. [Google Scholar] [CrossRef] [Green Version]
- Gleich, B.; Weizenecker, J. Tomographic imaging using the nonlinear response of magnetic particles. Nature 2005, 435, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Schrittwieser, S.; Pelaz, B.; Parak, W.J.; Lentijo-Mozo, S.; Soulantica, K.; Dieckhoff, J.; Ludwig, F.; Guenther, A.; Tschöpe, A.; Schotter, J. Homogeneous biosensing based on magnetic particle labels. Sensors 2016, 16, 828. [Google Scholar] [CrossRef] [PubMed]
- Ota, S.; Yamada, T.; Takemura, Y. Dipole-dipole interaction and its concentration dependence of magnetic fluid evaluated by alternating current hysteresis measurement. J. Appl. Phys. 2015, 117, 17D713. [Google Scholar] [CrossRef]
- Ilg, P. Equilibrium magnetization and magnetization relaxation of multicore magnetic nanoparticles. Phys. Rev. B 2017, 95, 214427. [Google Scholar] [CrossRef]
- Branquinho, L.C.; Carrião, M.S.; Costa, A.S.; Zufelato, N.; Sousa, M.H.; Miotto, R.; Ivkov, R.; Bakuzis, A.F. Effect of magnetic dipolar interactions on nanoparticle heating efficiency: Implications for cancer hyperthermia. Sci. Rep. 2013, 3, 2887. [Google Scholar] [CrossRef] [PubMed]
- Buzug, T.M.; Bringout, G.; Erbe, M.; Gräfe, K.; Graeser, M.; Grüttner, M.; Halkola, A.; Sattel, T.F.; Tenner, W.; Wojtczyk, H.; et al. Magnetic particle imaging: Introduction to imaging and hardware realization. Z. Med. Phys. 2012, 22, 323–334. [Google Scholar] [CrossRef] [PubMed]
- Trisnanto, S.B.; Kitamoto, Y. Field-dependent Brownian relaxation dynamics of a superparamagnetic clustered-particle suspension. Phys. Rev. E 2014, 90, 032306. [Google Scholar] [CrossRef] [PubMed]
- Jönsson, P.; García-Palacios, J.; Hansen, M.; Nordblad, P. Relaxation in interacting nanoparticle systems. J. Mol. Liq. 2004, 114, 131–135. [Google Scholar] [CrossRef]
- Jeun, M.; Lee, S.; Kang, J.K.; Tomitaka, A.; Kang, K.W.; Kim, Y.I.; Takemura, Y.; Chung, K.-W.; Kwak, J.; Bae, S. Physical limits of pure superparamagnetic Fe3O4 nanoparticles for a local hyperthermia agent in nanomedicine. Appl. Phys. Lett. 2012, 100, 092406. [Google Scholar] [CrossRef]
- Raĭkher, Y.L.; Pshenichnikov, A.F. Dynamic susceptibility of concentrated magnetic liquids. Sov. Phys. JETP Lett. 1985, 41, 132–135. Available online: http://www.jetpletters.ac.ru/ps/1442/article_21937.shtml (accessed on 6 June 2018).
- Shliomis, M.I.; Stepanov, V.I. Frequency dependence and long time relaxation of the susceptibility of the magnetic fluids. J. Magn. Magn. Mater. 1993, 122, 176–181. [Google Scholar] [CrossRef]
- Enpuku, K.; Sasayama, T.; Yoshida, T. Estimation of magnetic moment and anisotropy energy of magnetic markers for biosensing application. J. Appl. Phys. 2016, 119, 184902. [Google Scholar] [CrossRef]
- Yoshida, T.; Enpuku, K. Simulation and quantitative clarification of ac susceptibility of magnetic fluid in nonlinear Brownian relaxation region. Jpn. J. Appl. Phys. 2009, 48, 127002. [Google Scholar] [CrossRef]
- Yoshida, T.; Ogawa, K.; Enpuku, K.; Usuki, N.; Kanzaki, H. AC susceptibility of magnetic fluid in nonlinear Brownian relaxation region: Experiment and comparison with numerical simulation. Jpn. J. Appl. Phys. 2010, 49, 053001. [Google Scholar] [CrossRef]
- Dieckhoff, J.; Eberbeck, D.; Schilling, M.; Ludwig, F. Magnetic-field dependence of Brownian and Néel relaxation times. J. Appl. Phys. 2016, 119, 043903. [Google Scholar] [CrossRef]
- Brown, W.F., Jr. Thermal Fluctuations of a Single-Domain Particle. Phys. Rev. 1963, 130, 1677. [Google Scholar] [CrossRef]
- Bigot, J.-Y.; Vomir, M. Ultrafast magnetization dynamics of nanostructures. Ann. Phys. 2013, 525, 2–30. [Google Scholar] [CrossRef] [Green Version]
- Fannin, P.C.; Marin, C.N.; Raj, K.; Couper, C.; Barvinschi, P. An experimental study of the dynamic properties of nanoparticle colloids with identical magnetization but different particle size. J. Magn. Magn. Mater. 2012, 324, 3443–3447. [Google Scholar] [CrossRef] [Green Version]
- Verde, E.L.; Landi, G.T.; Carrião, M.S.; Drummond, A.L.; Gomes, J.A.; Vieira, E.D.; Sousa, M.H.; Bakuzis, A.F. Field dependent transition to the non-linear regime in magnetic hyperthermia experiments: Comparison between maghemite, copper, zinc, nickel and cobalt ferrite nanoparticles of similar sizes. AIP Adv. 2012, 2, 032120. [Google Scholar] [CrossRef] [Green Version]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trisnanto, S.B.; Takemura, Y. Complex Magnetization Harmonics of Polydispersive Magnetic Nanoclusters. Nanomaterials 2018, 8, 424. https://doi.org/10.3390/nano8060424
Trisnanto SB, Takemura Y. Complex Magnetization Harmonics of Polydispersive Magnetic Nanoclusters. Nanomaterials. 2018; 8(6):424. https://doi.org/10.3390/nano8060424
Chicago/Turabian StyleTrisnanto, Suko Bagus, and Yasushi Takemura. 2018. "Complex Magnetization Harmonics of Polydispersive Magnetic Nanoclusters" Nanomaterials 8, no. 6: 424. https://doi.org/10.3390/nano8060424
APA StyleTrisnanto, S. B., & Takemura, Y. (2018). Complex Magnetization Harmonics of Polydispersive Magnetic Nanoclusters. Nanomaterials, 8(6), 424. https://doi.org/10.3390/nano8060424