High-Performance Transmission of Surface Plasmons in Graphene-Covered Nanowire Pairs with Substrate
Abstract
:1. Introduction
2. Theoretical Model and Methodology
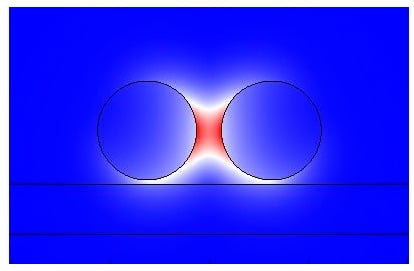
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ozbay, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef]
- Fang, Y.; Sun, M. Nanoplasmonic waveguides: Towards applications in integrated nanophotonic circuits. Light Sci. Appl. 2015, 4, e294. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83. [Google Scholar] [CrossRef]
- Kim, J.T.; Choi, S.Y. Graphene-based plasmonic waveguides for photonic integrated circuits. Opt. Express 2011, 19, 24557–24562. [Google Scholar] [CrossRef]
- Kim, J.T.; Yu, Y.J.; Choi, H.; Choi, C.G. Graphene-based plasmonic photodetector for photonic integrated circuits. Opt. Express 2014, 22, 803–808. [Google Scholar] [CrossRef] [PubMed]
- Sorger, V.J.; Oulton, R.F.; Ma, R.M.; Zhang, X. Toward integrated plasmonic circuits. MRS Bull. 2012, 37, 728–738. [Google Scholar] [CrossRef] [Green Version]
- Bian, Y.; Gong, Q. Metallic-nanowire-loaded silicon-on-insulator structures: A route to low-loss plasmon waveguiding on the nanoscale. Nanoscale 2015, 7, 4415–4422. [Google Scholar] [CrossRef] [PubMed]
- Bian, Y.; Zheng, Z.; Zhao, X.; Zhu, J.; Zhou, T. Symmetric hybrid surface plasmon polariton waveguides for 3D photonic integration. Opt. Express 2009, 17, 21320–21325. [Google Scholar] [CrossRef]
- Dai, D.; He, S. A silicon-based hybrid plasmonic waveguide with a metal cap for a nano-scale light confinement. Opt. Express 2009, 17, 16646–16653. [Google Scholar] [CrossRef]
- Liang, H.; Ruan, S.; Zhang, M.; Su, H.; Li, I.L. Modified surface plasmon polaritons for the nanoconcentration and long-range propagation of optical energy. Sci. Rep. 2014, 4, 5015. [Google Scholar] [CrossRef]
- Vlček, J.; Pištora, J.; Lesňák, M. Design of plasmonic-waveguiding structures for sensor applications. Nanomaterials 2019, 9, 1227. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, T.; Li, X.; Huang, W. Novel hybrid plasmonic waveguide consisting of two identical dielectric nanowires symmetrically placed on each side of a thin metal film. Opt. Express 2012, 20, 20535–20544. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.Z.; Aitchison, J.S.; Mojahedi, M. A marriage of convenience: Hybridization of surface plasmon and dielectric waveguide modes. Laser Photonics Rev. 2014, 8, 394–408. [Google Scholar] [CrossRef]
- Teng, D.; Cao, Q.; Wang, K. An extension of the generalized nonlocal theory for the mode analysis of plasmonic waveguides at telecommunication frequency. J. Opt. 2017, 19, 055003. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Shi, N.; Chen, Y.; Lu, X.; Wei, H.; Lu, Y.; Liu, N.; Zhang, B.; Wang, J. TM01 mode in a cylindrical hybrid plasmonic waveguide with large propagation length. Appl. Opt. 2018, 57, 4043–4047. [Google Scholar] [CrossRef]
- Veronis, G.; Fan, S. Modes of subwavelength plasmonic slot waveguides. J. Lightwave Technol. 2007, 25, 2511–2521. [Google Scholar] [CrossRef]
- Oulton, R.F.; Sorger, V.J.; Zentgraf, T.; Ma, R.M.; Gladden, C.; Dai, L.; Bartal, G.; Zhang, X. Plasmon lasers at deep subwavelength scale. Nature 2009, 461, 629. [Google Scholar] [CrossRef]
- Wu, H.; Gao, Y.; Xu, P.; Guo, X.; Wang, P.; Dai, D.; Tong, L. Plasmonic nanolasers: Pursuing extreme lasing conditions on nanoscale. Adv. Opt. Mater. 2019, 7, 1900334. [Google Scholar] [CrossRef]
- Guan, X.; Wu, H.; Shi, Y.; Dai, D. Extremely small polarization beam splitter based on a multimode interference coupler with a silicon hybrid plasmonic waveguide. Opt. Lett. 2014, 39, 259–262. [Google Scholar] [CrossRef]
- Noghani, M.T.; Samiei, M.H.V. Ultrashort hybrid metal–insulator plasmonic directional coupler. Appl. Opt. 2013, 52, 7498–7503. [Google Scholar] [CrossRef]
- Nielsen, M.G.; Bernardin, T.; Hassan, K.; Kriezis, E.E.; Weeber, J.C. Silicon-loaded surface plasmon polariton waveguides for nanosecond thermo-optical switching. Opt. Lett. 2014, 39, 2282–2285. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Xu, M.; Hu, X.; Wu, J.; Wang, T.; Su, Y. Monolithic silicon-based 16-QAM modulator using two plasmonic phase shifters. Opt. Commun. 2013, 286, 166–170. [Google Scholar] [CrossRef]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Modern Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Argyropoulos, C. Enhanced transmission modulation based on dielectric metasurfaces loaded with graphene. Opt. Express 2015, 23, 23787–23797. [Google Scholar] [CrossRef] [Green Version]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef]
- Vahed, H.; Ahmadi, S.S. Graphene-based plasmonic electro-optic modulator with sub-wavelength thickness and improved modulation depth. Appl. Phys. B 2017, 123, 265. [Google Scholar] [CrossRef]
- Ansell, D.; Radko, I.P.; Han, Z.; Rodriguez, F.J.; Bozhevolnyi, S.I.; Grigorenko, A.N. Hybrid graphene plasmonic waveguide modulators. Nat. Commun. 2015, 6, 8846. [Google Scholar] [CrossRef]
- Liu, J.P.; Wang, W.L.; Xie, F.; Luo, X.; Zhou, X.; Lei, M.; Yuan, Y.; Long, M.; Wang, L.L. Efficient directional coupling from multilayer-graphene-based long-range SPP waveguide to metal-based hybrid SPP waveguide in mid-infrared range. Opt. Express 2018, 26, 29509–29520. [Google Scholar] [CrossRef]
- Du, W.; Li, K.; Wu, D.; Jiao, K.; Jiao, L.; Liu, L.; Xia, F.; Kong, W.; Dong, L.; Yun, M. Electrically controllable directional coupler based on tunable hybrid graphene nanoplasmonic waveguide. Opt. Commun. 2019, 430, 450–455. [Google Scholar] [CrossRef]
- Guo, Z.; Nie, X.; Shen, F.; Zhou, H.; Zhou, Q.; Gao, J.; Guo, K. Actively tunable terahertz switches based on subwavelength graphene waveguide. Nanomaterials 2018, 8, 665. [Google Scholar] [CrossRef]
- Dai, Y.; Zhu, X.; Mortensen, N.A.; Zi, J.; Xiao, S. Nanofocusing in a tapered graphene plasmonic waveguide. J. Opt. 2015, 17, 065002. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, X.; Ma, Z.; Cai, W.; Wang, L.; Xu, J. Surface plasmon modes in graphene wedge and groove waveguides. Opt. Express 2013, 21, 32432–32440. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zhu, Y.Y.; Zhang, K.; Wu, H.W.; Peng, R.W.; Fan, R.H.; Wang, M. Plasmonic band structures in doped graphene tubes. Opt. Express 2017, 25, 12081–12089. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zeng, Y.; Xu, X.; Chen, X.; Zhou, Z.; Shi, P.; Yi, Z.; Ye, X.; Xiao, S.; Yi, Y. Plasmonic absorption enhancement in elliptical graphene arrays. Nanomaterials 2018, 8, 175. [Google Scholar] [CrossRef]
- Ding, Y.; Guan, X.; Zhu, X.; Hu, H.; Bozhevolnyi, S.I.; Oxenløwe, L.K.; Jin, K.J.; Mortensen, N.A.; Xiao, S. Efficient electro-optic modulation in low-loss graphene-plasmonic slot waveguides. Nanoscale 2017, 9, 15576–15581. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Zhang, T.; Chen, L.; Hong, W.; Li, X. A graphene-based hybrid plasmonic waveguide with ultra-deep subwavelength confinement. J. Lightwave Technol. 2014, 32, 4199–4203. [Google Scholar] [CrossRef]
- Liu, J.P.; Zhai, X.; Wang, L.L.; Li, H.J.; Xie, F.; Lin, Q.; Xia, S.X. Analysis of mid-infrared surface plasmon modes in a graphene-based cylindrical hybrid waveguide. Plasmonics 2016, 11, 703–711. [Google Scholar] [CrossRef]
- Liu, J.P.; Zhai, X.; Wang, L.L.; Li, H.J.; Xie, F.; Xia, S.X.; Shang, X.J.; Luo, X. Graphene-based long-range SPP hybrid waveguide with ultra-long propagation length in mid-infrared range. Opt. Express 2016, 24, 5376–5386. [Google Scholar] [CrossRef]
- Chen, M.; Sheng, P.; Sun, W.; Cai, J. A symmetric terahertz graphene-based hybrid plasmonic waveguide. Opt. Commun. 2016, 376, 41–46. [Google Scholar] [CrossRef]
- Ye, L.; Sui, K.; Liu, Y.; Zhang, M.; Liu, Q.H. Graphene-based hybrid plasmonic waveguide for highly efficient broadband mid-infrared propagation and modulation. Opt. Express 2018, 26, 15935–15947. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, H.; Wang, S.; Cai, M.; Ma, L. Optical transport properties of graphene surface plasmon polaritons in Mid-Infrared band. Crystals 2019, 9, 354. [Google Scholar] [CrossRef]
- He, X.; Ning, T.; Zheng, J.; Li, J.; Pei, L.; Wu, B. Deep-subwavelength light transmission in hybrid graphene-dielectric slot waveguide. J. Opt. 2019, 21, 095001. [Google Scholar] [CrossRef]
- Chen, B.; Meng, C.; Yang, Z.; Li, W.; Lin, S.; Gu, T.; Guo, X.; Wang, D.; Yu, S.; Wong, C.; et al. Graphene coated ZnO nanowire optical waveguides. Opt. Express 2014, 22, 24276–24285. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhang, X.; Zhang, H.; Xu, M. Graphene covered on microfiber exhibiting polarization and polarization-dependent saturable absorption. IEEE J. Sel. Top. Quantum Electron. 2013, 20, 55–61. [Google Scholar]
- Gao, Y.; Ren, G.; Zhu, B.; Liu, H.; Lian, Y.; Jian, S. Analytical model for plasmon modes in graphene-coated nanowire. Opt. Express 2014, 22, 24322–24331. [Google Scholar] [CrossRef]
- Gao, Y.; Ren, G.; Zhu, B.; Wang, J.; Jian, S. Single-mode graphene-coated nanowire plasmonic waveguide. Opt. Lett. 2014, 39, 5909–5912. [Google Scholar] [CrossRef]
- Hajati, M.; Hajati, Y. High-performance and low-loss plasmon waveguiding in graphene-coated nanowire with substrate. J. Opt. Soc. Am. B 2016, 33, 2560–2565. [Google Scholar] [CrossRef]
- Wu, D.; Tian, J.; Yang, R. Study of mode performances of graphene-coated nanowire integrated with triangle wedge substrate. J. Nonlinear Opt. Phys. Mater. 2018, 27, 1850013. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Yin, H.; Zhang, M.; Su, H.; Li, I.L.; Liang, H. Graphene-coated nanowires with a drop-shaped cross section for 10 nm confinement and 1 mm propagation. Opt. Lett. 2017, 42, 2078–2081. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, L.; Zhang, S.; Cao, T.; Alù, A.; Ruan, S.; Qiu, C.W. Gate-programmable electro-optical addressing array of graphene-coated nanowires with sub-10 nm resolution. ACS Photonics 2016, 3, 1847–1853. [Google Scholar] [CrossRef]
- Li, R.; Wang, H.; Zheng, B.; Dehdashti, S.; Li, E.; Chen, H. Bistable scattering in graphene-coated dielectric nanowires. Nanoscale 2017, 9, 8449–8457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuzmin, D.A.; Bychkov, I.V.; Shavrov, V.G.; Temnov, V.V.; Lee, H.I.; Mok, J. Plasmonically induced magnetic field in graphene-coated nanowires. Opt. Lett. 2016, 41, 396–399. [Google Scholar] [CrossRef] [PubMed]
- Teng, D.; Wang, K.; Li, Z.; Zhao, Y.; Zhao, G.; Li, H.; Wang, H. Graphene-coated elliptical nanowires for low loss subwavelength terahertz transmission. Appl. Sci. 2019, 9, 2351. [Google Scholar] [CrossRef]
- Zhu, B.; Ren, G.; Yang, Y.; Gao, Y.; Wu, B.; Lian, Y.; Wang, J.; Jian, S. Field enhancement and gradient force in the graphene-coated nanowire pairs. Plasmonics 2015, 10, 839–845. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Li, Z.; Zhao, Y. Graphene-coated nanowire dimers for deep subwavelength waveguiding in mid-infrared range. Opt. Express 2019, 27, 12458–12469. [Google Scholar] [CrossRef]
- Wu, D.; Tian, J. Study on the plasmonic characteristics of bow-tie type graphene-coated nanowire pair. Optik 2018, 156, 689–695. [Google Scholar] [CrossRef]
- Yan-Ling, P.; Wen-Rui, X.; Zhuang-Zhi, W.; Chang-Yong, L. Mode properties analysis of graphene-coated asymmetric parallel dielectric nanowire waveguides. Acta Phys. Sin. 2018, 67, 038102. [Google Scholar]
- Nikitin, A.Y.; Guinea, F.; Garcia-Vidal, F.J.; Martin-Moreno, L. Fields radiated by a nanoemitter in a graphene sheet. Phys. Rev. B 2011, 84, 195446. [Google Scholar] [CrossRef] [Green Version]
- Francescato, Y.; Giannini, V.; Maier, S.A. Strongly confined gap plasmon modes in graphene sandwiches and graphene-on-silicon. New J. Phys. 2013, 15, 063020. [Google Scholar] [CrossRef]
- Oulton, R.F.; Sorger, V.J.; Genov, D.A.; Pile, D.F.P.; Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photonics 2008, 2, 496. [Google Scholar] [CrossRef]
- Buckley, R.; Berini, P. Figures of merit for 2D surface plasmon waveguides and application to metal stripes. Opt. Express 2007, 15, 12174–12182. [Google Scholar] [CrossRef] [PubMed]






| Substrate Permittivity ε2 | Lp/μm | Aeff/A0 | FoM |
|---|---|---|---|
| 2.25 | 15.23 | 2.75 × 10−4 | 140.9 |
| 4 | 14.41 | 2.42 × 10−4 | 138.3 |
| 6 | 13.46 | 9.61 × 10−5 | 134.4 |
| 8 | 12.48 | 4.53 × 10−5 | 129.6 |
| 12.25 | 10.28 | 1.19 × 10−5 | 116.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, D.; Wang, K.; Huan, Q.; Zhao, Y.; Tang, Y. High-Performance Transmission of Surface Plasmons in Graphene-Covered Nanowire Pairs with Substrate. Nanomaterials 2019, 9, 1594. https://doi.org/10.3390/nano9111594
Teng D, Wang K, Huan Q, Zhao Y, Tang Y. High-Performance Transmission of Surface Plasmons in Graphene-Covered Nanowire Pairs with Substrate. Nanomaterials. 2019; 9(11):1594. https://doi.org/10.3390/nano9111594
Chicago/Turabian StyleTeng, Da, Kai Wang, Qiongsha Huan, Yongzhe Zhao, and Yanan Tang. 2019. "High-Performance Transmission of Surface Plasmons in Graphene-Covered Nanowire Pairs with Substrate" Nanomaterials 9, no. 11: 1594. https://doi.org/10.3390/nano9111594
APA StyleTeng, D., Wang, K., Huan, Q., Zhao, Y., & Tang, Y. (2019). High-Performance Transmission of Surface Plasmons in Graphene-Covered Nanowire Pairs with Substrate. Nanomaterials, 9(11), 1594. https://doi.org/10.3390/nano9111594