Multi-Response Optimization of Surface Grinding Process Parameters of AISI 4140 Alloy Steel Using Response Surface Methodology and Desirability Function under Dry and Wet Conditions
Abstract
:1. Introduction
- Experimentally investigation the influence of the input machining parameters (cross-feed, workpiece velocity, wheel velocity, and the depth of cut) on three responses (contact temperature, material removal rate (MRR), and machining cost) during surface grinding of AISI 4140 steel.
- Establishment of an empirical equation of each output responses in terms of input parameters based on the experimental data. Further this mathematical model is used to predict the output responses.
- Optimization of the output responses (minimum contact temperature, maximum MRR, and minimum machining cost) based on the DFA methodology. Further, optimal set of input parameters are investigated for these optimal responses.
2. Methodology and Experimental Procedures
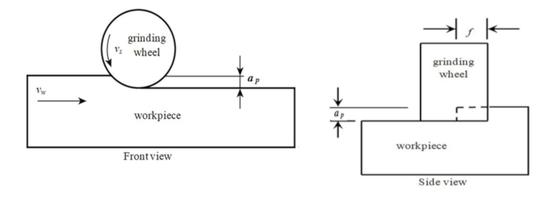
2.1. Materials and Instruments
2.2.1. Experimental Set Up
2.2.2. Material Removal Rate (MRR) Calculation
- MRR is the material removal rate (mm3/min)
- vw is the workpiece velocity or longitudinal table travel velocity (m/min)
- ap is the depth of cut (mm)
- b is the width of the cut (mm).
2.2.3. Response Surface Methodology
2.2.4. Desirability Function Approach
- Xi—input variables value for i in the experiment, I = 1, 2,…, m.
3. Results and Discussions
4. Conclusions
- The wet condition dominates the overall desirability when the temperature is given the highest (≥20%) weightage. As our optimization goal was minimum temperature, the obtained result is as expected. Since the wet conditions keep the temperature down, the obtained result is achieved so. Again, in current scenario, cross-feed, wheel velocity, and depth of cut were at the lowest levels as a higher value of these parameter increases the amount of material removal per pass leading to increased temperature.
- Dry condition achieves the highest overall desirability if the cost is given the highest priority instead. As the optimization goal was minimum cost, the obtained result is as expected. The underlying reason of the obtained result is no use of cutting fluid in the dry condition, hence cost is reduced. However, in the wet condition, cost is added due to cost of cutting fluid and extra power consumption. Again, in the current scenario, except depth of cut and wheel velocity, all other input parameters are at their upper limit. This provides a higher material removal leading to short machining time and reduced cost. However, depth of cut and wheel velocity at its upper limit provides larger power consumption which in turn increases cost. Thus, depth of cut and wheel velocity was kept at the lowest level.
- If MRR is given priority (20:40:40), i.e., quick material removal, then all the input parameters are set at their highest level along with the wet machining condition. Larger MRR require higher cross-feed, depth of cut, wheel velocity, and higher workpiece velocity. Due to higher MRR, quick removal of chips is required which is very effective with wet machining condition. The obtained result exists at two levels of wheel velocity (15 and 25 m/s). At higher wheel velocity, grinding zone temperature is higher, which is expected. However, it may lead to poor surface quality. Hence, lower wheel velocity is found to be more suitable for grinding.
- For equal weights of responses, the optimal values are found to be 6 mm/pass of cross-feed, 12 m/min of workpiece velocity, 15 m/s of the wheel or cutting velocity, 0.095 mm of the depth of cut in wet condition, with a maximum overall desirability value of 0.863. Optimum value for other weights of responses can be found in Table 8.
- For dry cutting condition, keeping other parameters constant, desirability value increases with higher values of depth of cut until 0.095 mm, from where it decreases. This is because, up to a certain increase in depth of cut, high temperature is produced which drives the overall desirability down. If depth of cut is kept constant instead, then a positive relationship between the overall desirability values, and cross-feed and workpiece velocity is observed.
- For the wet conditions, it is observed that workpiece velocity and cross-feed are positively related to the higher overall desirability values whereas the depth of cut and wheel velocity have negligible effects.
- For a specific weight assignment, it is evident that the depth of cut positively affects the overall desirability values in the dry cutting condition, but it has a negligible effect in the wet condition.
- It must be kept in mind that these conjectures are not invariable; rather it depends on how the weights are assigned. Wheel velocity has no apparent effect on desirability when all weights are equal in our case. However, this scenario will most likely change if different weights are assigned.
- The confirmatory experiments corroborate that the predicted responses are in good agreement with the experimental results.
5. Strength and Limitations of the Study
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ap | depth of cut (mm) |
| b | width of the cut (mm) |
| b0, bi, bii, bij | coefficient of intercept, linear, quadratic and interaction of input variables respectively |
| bjo, bjk, bjkk, bjkl | are the regression coefficients |
| Costdry | total cost at dry machining condition (BDT) |
| Costwet | total cost at wet machining condition (BDT) |
| Di | overall desirability of all responses |
| api | the depth of cut at experiment i |
| = 0 | denotes the lowest desirability value of output response (Yij) |
| = 1 | denotes the highest desirability value of output response (Yij) |
| fb | cross-feed (mm/pass) |
| fbi | cross-feed at experiment i |
| Gij | target value of the jth response (Yij) |
| maximum goal of output j at experiment i | |
| minimum goal of output j at experiment i | |
| m | no. of experimental runs |
| Mij | lower level of output j at experiment i |
| MRR | material removal rate (mm3/s) |
| n | no. of output responses variables |
| Nij | higher level of output j at experiment i |
| p | no. of input independent parameters |
| Tempdry | Temperature at dry machining condition (°C) |
| Tempwet | Temperature at wet machining condition (°C) |
| vs | wheel velocity (m/s) |
| vsi | the wheel velocity at experiment i |
| vw | workpiece velocity or longitudinal table travel velocity (m/min) |
| vwi | workpiece velocity at experiment i |
| Yij | output responses value at ith experiment of jth response, j = 1, 2,…, n |
References
- Chattopadhyay, A. Machining and Machine Tools (With CD); John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gupta, M.K.; Khan, A.M.; Song, Q.; Liu, Z.; Khalid, Q.S.; Jamil, M.; Kuntoğlu, M.; Usca, Ü.A.; Sarıkaya, M.; Pimenov, D.Y. A review on conventional and advanced minimum quantity lubrication approaches on performance measures of grinding process. Int. J. Adv. Manuf. Technol. 2021, 117, 729–750. [Google Scholar] [CrossRef]
- Malkin, S.; Guo, C. Grinding Technology: Theory and Application of Machining with Abrasives; Industrial Press Inc.: New York, NY, USA, 2008. [Google Scholar]
- Leskovar, P.; Grum, J. The metallurgical aspects of machining. CIRP Ann. 1986, 35, 537–550. [Google Scholar] [CrossRef]
- Tönshoff, H.; Brinksmeier, E. Determination of the mechanical and thermal influences on machined surfaces by microhardness and residual stress analysis. CIRP Ann. 1980, 29, 519–530. [Google Scholar] [CrossRef]
- Rowe, W.B. Principles of Modern Grinding Technology; William Andrew: Norwich, NY, USA, 2013. [Google Scholar]
- Guo, G.; Liu, Z.; An, Q.; Chen, M. Experimental investigation on conventional grinding of Ti-6Al-4V using SiC abrasive. Int. J. Adv. Manuf. Technol. 2011, 57, 135–142. [Google Scholar] [CrossRef]
- Howes, T.; Tönshoff, H.; Heuer, W.; Howes, T. Environmental aspects of grinding fluids. CIRP Ann. 1991, 40, 623–630. [Google Scholar] [CrossRef]
- Jawahir, I.; Brinksmeier, E.; M’saoubi, R.; Aspinwall, D.; Outeiro, J.; Meyer, D.; Umbrello, D.; Jayal, A. Surface integrity in material removal processes: Recent advances. CIRP Ann. 2011, 60, 603–626. [Google Scholar] [CrossRef]
- Sharma, C.; Ghosh, S.; Talukdar, P. Finite element analysis of workpiece temperature during surface grinding of inconel 718 alloy. In Proceedings of the 5th International & 26th All India Manufacturing Technology, Design and Research Conference, IIT Guwahati, Assam, India, 12–14 December 2014; pp. 420–421. [Google Scholar]
- Guo, C.; Wu, Y.; Varghese, V.; Malkin, S. Temperatures and energy partition for grinding with vitrified CBN wheels. CIRP Ann. 1999, 48, 247–250. [Google Scholar] [CrossRef]
- Upadhyaya, R.; Malkin, S. Thermal aspects of grinding with electroplated CBN wheels. J. Manuf. Sci. Eng. 2004, 126, 107–114. [Google Scholar] [CrossRef]
- Yao, C.; Wang, T.; Xiao, W.; Huang, X.; Ren, J. Experimental study on grinding force and grinding temperature of Aermet 100 steel in surface grinding. J. Mater. Process. Technol. 2014, 214, 2191–2199. [Google Scholar] [CrossRef]
- Johnson, R.T.; Parker, P.A.; Montgomery, D.C.; Cutler, A.D.; Danehy, P.M.; Rhew, R.D. Design strategies for response surface models for the study of supersonic combustion. Qual. Reliab. Eng. Int. 2009, 25, 365–377. [Google Scholar] [CrossRef]
- Bhushan, R.K. Optimization of cutting parameters for minimizing power consumption and maximizing tool life during machining of Al alloy SiC particle composites. J. Clean. Prod. 2013, 39, 242–254. [Google Scholar] [CrossRef]
- Rudrapati, R.; Pal, P.K.; Bandyopadhyay, A. Modeling and optimization of machining parameters in cylindrical grinding process. Int. J. Adv. Manuf. Technol. 2016, 82, 2167–2182. [Google Scholar] [CrossRef]
- Janardhan, M.; Krishna, A.G. Multi-objective optimization of cutting parameters for surface roughness and metal removal rate in surface grinding using response surface methodology. Int. J. Adv. Eng. Technol. 2012, 3, 270. [Google Scholar]
- Periyasamy, S.; Aravind, M.; Vivek, D.; Amirthagadeswaran, K. Optimization of Surface Grinding Process Parameters for Minimum Surface Roughness in AISI 1080 Using Response Surface Methodology. Adv. Mater. Res. 2014, 984–985, 118–123. [Google Scholar] [CrossRef]
- Venkatesan, K.; Devendiran, S.; Sachin, D.; Swaraj, J. Investigation of machinability characteristics and comparative analysis under different machining conditions for sustainable manufacturing. Measurement 2020, 154, 107425. [Google Scholar] [CrossRef]
- Manohar, M.; Joseph, J.; Selvaraj, T.; Sivakumar, D. Application of desirability-function and RSM to optimise the multi-objectives while turning Inconel 718 using coated carbide tools. Int. J. Manuf. Technol. Manag. 2013, 27, 218–237. [Google Scholar] [CrossRef]
- Naresh, N.; Rajasekhar, K. Multi-response optimization for milling AISI 304 Stainless steel using GRA and DFA. Adv. Mater. Res. 2016, 5, 67–80. [Google Scholar] [CrossRef]
- Buranská, E.; Buranský, I. Cutting Environment Impact on the Aluminium Alloy Machining (DFA). In Proceedings of the 29th DAAAM International Symposium, Zadar, Croatia, 21–28 October 2018; pp. 1158–1163. [Google Scholar]
- Borchers, F.; Clausen, B.; Eckert, S.; Ehle, L.; Epp, J.; Harst, S.; Hettig, M.; Klink, A.; Kohls, E.; Meyer, H.; et al. Comparison of Different Manufacturing Processes of AISI 4140 Steel with Regard to Surface Modification and Its Influencing Depth. Metals 2020, 10, 895. [Google Scholar] [CrossRef]
- Saravanan, R.; Asokan, P.; Sachidanandam, M. A multi-objective genetic algorithm (GA) approach for optimization of surface grinding operations. Int. J. Mach. Tools Manuf. 2002, 42, 1327–1334. [Google Scholar] [CrossRef]
- Pawar, P.; Rao, R.; Davim, J. Multiobjective optimization of grinding process parameters using particle swarm optimization algorithm. Mater. Manuf. Process. 2010, 25, 424–431. [Google Scholar] [CrossRef]
- Alajmi, M.S.; Alfares, F.S.; Alfares, M.S. Selection of optimal conditions in the surface grinding process using the quantum based optimisation method. J. Intell. Manuf. 2019, 30, 1469–1481. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, M.; Li, J.; Ming, W.; Shao, X.; Huang, Y. Multi-objective optimization for surface grinding process using a hybrid particle swarm optimization algorithm. Int. J. Adv. Manuf. Technol. 2014, 71, 1861–1872. [Google Scholar] [CrossRef]
- Gholami, M.H.; Azizi, M.R. Constrained grinding optimization for time, cost, and surface roughness using NSGA-II. Int. J. Adv. Manuf. Technol. 2014, 73, 981–988. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. Optimization of time, cost and surface roughness in grinding process using a robust multi-objective dragonfly algorithm. Neural Comput. Appl. 2020, 32, 3987–3998. [Google Scholar] [CrossRef]
- Öztürk, S.; Kahraman, M.F. Modeling and optimization of machining parameters during grinding of flat glass using response surface methodology and probabilistic uncertainty analysis based on Monte Carlo simulation. Measurement 2019, 145, 274–291. [Google Scholar] [CrossRef]
- Shin, T.M.; Adam, A.; Abidin, A.F.Z. A comparative study of PSO, GSA and SCA in parameters optimization of surface grinding process. Bull. Electr. Eng. Inform. 2019, 8, 1117–1127. [Google Scholar] [CrossRef]
- Bardhan, P.K.; Bhunia, B.; Goswami, S.; Chandra, P. Optimization of Process Parameters of Surface Grinding of AISI 304 Steel with Al2O3 Abrasive Wheel. In Proceedings of the International Conference on Industry Interactive Innovations in Science, Engineering and Technology (I3SET2K19), Kalyani, India, 13–14 December 2019. [Google Scholar]
- Sanjeevi, R.; Kumar, G.A.; Krishnan, B.R. Optimization of machining parameters in plane surface grinding process by response surface methodology. Mater. Today Proc. 2020, 37, 85–87. [Google Scholar] [CrossRef]
- Dambatta, Y.S.; Sayuti, M.; Sarhan, A.A.; Hamdi, M. Comparative study on the performance of the MQL nanolubricant and conventional flood lubrication techniques during grinding of Si3N4 ceramic. Int. J. Adv. Manuf. Technol. 2018, 96, 3959–3976. [Google Scholar] [CrossRef]
- Maier, M.; Rupenyan, A.; Bobst, C.; Wegener, K. Self-optimizing grinding machines using Gaussian process models and constrained Bayesian optimization. Int. J. Adv. Manuf. Technol. 2020, 108, 539–552. [Google Scholar] [CrossRef]
- Ronoh, K.N.; Mwema, F.M.; Akinlabi, S.A.; Akinlabi, E.T.; Karuri, N.W.; Ngetha, H.T. Effects of cooling conditions and grinding depth on sustainable surface grinding of Ti-6Al-4V: Taguchi approach. AIMS Mater. Sci. 2019, 6, 697–712. [Google Scholar] [CrossRef]
- Tung, L.A.; Pi, V.N.; Ha, D.T.T.; Hung, L.X.; Banh, T.L. A study on optimization of surface roughness in surface grinding 9CrSi tool steel by using Taguchi method. In Advances in Engineering Research and Application, Proceedings of the International Conference on Engineering Research and Applications, ICERA 2019, Thai Nguyen, Vietnam, 1–2 December 2019; Sattler, K.-U., Nguyen, D.C., Vu, N.P., Long, B.T., Puta, H., Eds.; Springer: Cham, Switzerland, 2020; pp. 100–108. [Google Scholar]
- Singh, H.; Sharma, V.S.; Dogra, M. Exploration of graphene assisted vegetables oil based minimum quantity lubrication for surface grinding of TI-6AL-4V-ELI. Tribol. Int. 2020, 144, 106113. [Google Scholar] [CrossRef]
- Patil, P.J.; Patil, C. Analysis of process parameters in surface grinding using single objective Taguchi and multi-objective grey relational grade. Perspect. Sci. 2016, 8, 367–369. [Google Scholar] [CrossRef] [Green Version]
- Rabiei, F.; Rahimi, A.; Hadad, M.; Ashrafijou, M. Performance improvement of minimum quantity lubrication (MQL) technique in surface grinding by modeling and optimization. J. Clean. Prod. 2015, 86, 447–460. [Google Scholar] [CrossRef]
- Rabiei, F.; Rahimi, A.; Hadad, M. Performance improvement of eco-friendly MQL technique by using hybrid nanofluid and ultrasonic-assisted grinding. Int. J. Adv. Manuf. Technol. 2017, 93, 1001–1015. [Google Scholar] [CrossRef]
- Puri, A.B.; Banerjee, S. Multiple-response optimisation of electrochemical grinding characteristics through response surface methodology. Int. J. Adv. Manuf. Technol. 2013, 64, 715–725. [Google Scholar] [CrossRef]
- Khan, A.M.; Jamil, M.; Mia, M.; Pimenov, D.Y.; Gasiyarov, V.R.; Gupta, M.K.; He, N. Multi-objective optimization for grinding of AISI D2 steel with Al2O3 wheel under MQL. Materials 2018, 11, 2269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palanikumar, K. Modeling and analysis for surface roughness in machining glass fibre reinforced plastics using response surface methodology. Mater. Des. 2007, 28, 2611–2618. [Google Scholar] [CrossRef]
- Celep, O.; Aslan, N.; Alp, İ.; Taşdemir, G. Optimization of some parameters of stirred mill for ultra-fine grinding of refractory Au/Ag ores. Powder Technol. 2011, 208, 121–127. [Google Scholar] [CrossRef]
- Krajnik, P.; Kopac, J.; Sluga, A. Design of grinding factors based on response surface methodology. J. Mater. Process. Technol. 2005, 162, 629–636. [Google Scholar] [CrossRef]
- Pradhan, M.K.; Biswas, C.K. Modeling of residual stresses of EDMed AISI 4140 Steel. In Proceedings of the International Conference on Recent Advances in Materials, Processing and Characterization, VRS Engineering College, Vijayawada, India, 3–4 July 2008; pp. 49–55. [Google Scholar]
- Khuri, A.I. 12 Multiresponse surface methodology. Handb. Stat. 1996, 13, 377–406. [Google Scholar]
- Harrington, E.C. The desirability function. Ind. Qual. Control 1965, 21, 494–498. [Google Scholar]
- Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Pignatiello Jr, J.J. Strategies for robust multiresponse quality engineering. IIE Trans. 1993, 25, 5–15. [Google Scholar] [CrossRef]
- Ryan, T.P.; Morgan, J. Modern experimental design. J. Stat. Theory Pract. 2007, 1, 501–506. [Google Scholar] [CrossRef]
- Sadeghi, M.; Hadad, M.; Tawakoli, T.; Vesali, A.; Emami, M. An investigation on surface grinding of AISI 4140 hardened steel using minimum quantity lubrication-MQL technique. Int. J. Mater. Form. 2010, 3, 241–251. [Google Scholar] [CrossRef]










| Type of Grinding | Material Used | Parameter Optimized | Optimized Output | Analysis Technique | Ref. |
|---|---|---|---|---|---|
| Dry grinding | Mild steel | Wheel speed, workpiece speed, depth of dressing and lead of dressing | Minimum production cost, maximum production rate and the finest possible surface grinding finish | Genetic Algorithm (GA) | [24] |
| Mild Steel | Wheel speed, workpiece speed, depth of dressing and lead of dressing | Production cost, production rate and surface finish | Particle swarm optimization (PSO) algorithm | [25] | |
| Mild Steel | Wheel speed, workpiece speed, depth of dressing and lead of dressing | Production cost, production rate and surface finish | Quantum Based Optimization Method (QBOM) | [26] | |
| Mild Steel | Wheel speed, workpiece speed, depth of dressing and lead of dressing | Production cost, production rate and surface roughness | Hybrid Particle Swarm Optimization (HPSO) algorithm | [27] | |
| 1.2080 Steel | Wheel speed, workpiece speed and depth of cut | Surface finish, total grinding time and production cost | Non-dominated sorting genetic algorithm (NSGA II) | [28] | |
| 1.2080 Steel | Wheel speed, workpiece speed and depth of cut | Surface quality, total grinding time and production cost | Dragonfly algorithm | [29] | |
| EN24 steel | Wheel speed, table speed and depth of cut | Surface roughness and metal removal rate | RSM optimization | [17] | |
| Soda-lime glass | Wheel speed, depth of cut and feed rate | Surface roughness | RSM and Monte Carlo Simulation | [30] | |
| Steel | Speed of wheel, speed of workpiece, depth of dressing and lead of dressing | Production cost, production rate and surface finish | Particle swarm optimization, Gravitational search algorithm and Sine Cosine algorithm | [31] | |
| Stainless steel material AISI 304 | Feed rate, speed of table and depth of cut | MRR and surface roughness | ANOVA, Taguchi method | [32] | |
| EN 24 steel | Wheel speed, depth of cut and feed rate timing | Surface roughness | RSM | [33] | |
| Conventional grinding | Silicon nitride ceramic | Feed rate, depth of cut, type of diamond wheel and lubrication type | Grinding forces, workpiece surfaceroughness, surface damages and wheel wear | Adaptiveneuro-fuzzy inference system (ANFIS) and Taguchi method | [34] |
| Tungsten carbide insert | Feed rate and cutting speed | Production costs, grinding burn, surface roughness and temperature at the grinding surface | Constrained Bayesian optimization combined with Gaussian process Models | [35] | |
| Ti-6Al-4V | Coolant types, cooling techniques and grinding depths | Surface hardness and surface morphology | Taguchi method and ANOVA | [36] | |
| 9CrSi annealing tool steel | Coolant concentration, coolant flow, cross-feed, table speed and depth of cut | Surface roughness | Taguchi method | [37] | |
| Ti-6Al-4V-ELI | Types of coolant and graphene percentage in the coolant | Surface roughness, grinding force, specific grinding energy and coefficient-of-friction | Experimental (conventional) | [38] | |
| MQL grinding | EN8 flat plate | Depth of cut, type of lubricant, feed rate, grinding wheel speed, coolant flow rate and nanoparticlesize | G ratio and surface finish | Taguchi based Grey relational analysis, ANOVA | [39] |
| Two soft steels (CK45 and S305) and two hard steels (HSS and 100Cr6) | Depth of cut, cutting speed and feed rate | Grinding forces, friction coefficient, surface roughness, surface morphology and form of the chips | RSM, ANOVA, GA | [40] | |
| Electrochemical grinding | 100Cr6 hardened steel (bearing steel) | Specific material removal rate | Maximum temperature, grinding forces and friction coefficient | Experimental (conventional) | [41] |
| Composite carbide inserts | Voltage and cutting speed | Current density, material removal rate (MRR) and surface finish | Response surface methodology (RSM), Desirability function | [42] |
| Properties | Specification | |||||||
|---|---|---|---|---|---|---|---|---|
| Work material | AISI 4140 alloy steel | |||||||
| Dimension | 72 mm × 37 mm × 27.3 mm | |||||||
| Type | Solid | |||||||
| Chemical composition | Carbon | Chromium | Iron | Manganese | Molybdenum | Phosphorous | Silicon | Sulfur |
| 0.380–0.430 | 0.8–1.10 | Balance | 0.75–1.0 | 0.15–0.25 | 0.035 | 0.15–0.30 | 0.040 | |
| Hardness | 40 HRC | |||||||
| Tensile strength | 655 MPa | |||||||
| Yield strength | 415 MPa | |||||||
| Hardness, Brinell | 197 | |||||||
| Density | 7.85 g/cm3 | |||||||
| Melting point | 1416 °C | |||||||
| Grinding Conditions with Specification | Grinding mode | Single pass surface grinding, down cut |
| Grinding machine | Okamoto hydraulic surface grinder | |
| Nozzle angle | 15° | |
| Flow rate | 5 L/min | |
| Flow measuring device | Z-5615 Panel Flowmeter | |
| Machining condition | Dry, Wet (Flood) | |
| Labor cost | 0.06 BDT/s | |
| Power consumption cost | 8 BDT/unit | |
| Cutting fluid cost | 0.5 BDT/s | |
| Dressing Cut Parameter | Dresser | Single point diamond, HS050 |
| Total depth of dressing | 300 μm | |
| Dressing speed | 400 mm/min | |
| Grinding wheel wear per dress, radially | 3.75 μm |
| SI. No. | Grinding Input Parameters | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| 1 | Workpiece velocity, vw (m/min) | 5 | 12 | - | - | - |
| 2 | Wheel velocity, vs (m/s) | 15 | 25 | - | - | - |
| 3 | Depth of cut, ap (mm) | 0.07 | 0.08 | 0.09 | 0.095 | 0.10 |
| 4 | Cross-feed, fb (mm/pass) | 3 | 6 | - | - | - |
| 5 | Cutting condition | Dry | Wet | - | - | - |
| Objectives | Parameters/ Condition | Workpiece Velocity, vw (m/min) | Wheel Velocity, vs (m/s) | Depth of Cut, ap mm | Cross-Feed, fb (mm/Pass) |
|---|---|---|---|---|---|
| The optimum level for temp | Dry | 12–20 | 2–10 | 0.065–0.085 | 0.1–2.5 |
| The optimum level for the cost | 12–15 | - | 0.03–0.13 | 6.5–8 | |
| The optimum level for temp | Wet | 15–20 | 1–12 | 0.062–0.080 | - |
| The optimum level for the cost | 15–20 | - | - | 7–10 |
| Variable Type | Variables | Target | Lower Bound | Upper Bound |
|---|---|---|---|---|
| Independent (input parameters) | Cutting condition | Dry or Wet | N/A | N/A |
| Cross-feed (mm/pass) | In range | 3 | 6 | |
| Workpiece velocity (m/min) | In range | 5 | 12 | |
| Wheel velocity (m/s) | In range | 15 | 25 | |
| Depth of cut (mm) | In range | 0.07 | 0.10 | |
| Dependent (response) | Temperature (°C) | Minimize | 109.78 | 313.67 |
| MRR (mm3/min) | Maximize | 1050 | 7200 | |
| Total cost (BDT) | Minimize | 0.91 | 29.48 |
| Individual Desirability | Overall Desirability (Equal Weightage 33:33:33) | Overall Desirability (20:40:40) | Overall Desirability (15:25:60) | ||
|---|---|---|---|---|---|
| Temp. | MRR | Total Cost | |||
| 0.533 | 0 | 0.890 | 0 | 0 | 0 |
| 0.527 | 0.025 | 0.891 | 0.228 | 0.193 | 0.338 |
| 0.377 | 0.049 | 0.891 | 0.255 | 0.236 | 0.380 |
| 0.249 | 0.061 | 0.891 | 0.239 | 0.237 | 0.377 |
| 0.086 | 0.074 | 0.891 | 0.179 | 0.207 | 0.337 |
| 0.458 | 0 | 0.888 | 0 | 0 | 0 |
| 0.456 | 0.025 | 0.890 | 0.217 | 0.187 | 0.330 |
| 0.312 | 0.049 | 0.890 | 0.240 | 0.227 | 0.369 |
| 0.186 | 0.061 | 0.890 | 0.217 | 0.223 | 0.361 |
| 0.024 | 0.074 | 0.890 | 0.117 | 0.160 | 0.278 |
| 0.615 | 0.240 | 0.969 | 0.524 | 0.507 | 0.639 |
| 0.601 | 0.298 | 0.970 | 0.559 | 0.550 | 0.673 |
| 0.444 | 0.357 | 0.970 | 0.537 | 0.557 | 0.672 |
| 0.311 | 0.386 | 0.970 | 0.489 | 0.535 | 0.650 |
| 0.144 | 0.415 | 0.970 | 0.388 | 0.472 | 0.590 |
| 0.542 | 0.240 | 0.968 | 0.502 | 0.494 | 0.627 |
| 0.532 | 0.298 | 0.969 | 0.536 | 0.537 | 0.660 |
| 0.379 | 0.357 | 0.969 | 0.509 | 0.539 | 0.656 |
| 0.249 | 0.386 | 0.969 | 0.454 | 0.511 | 0.628 |
| 0.084 | 0.415 | 0.969 | 0.324 | 0.424 | 0.544 |
| 0.487 | 0.171 | 0.954 | 0.431 | 0.420 | 0.562 |
| 0.484 | 0.220 | 0.953 | 0.467 | 0.463 | 0.597 |
| 0.339 | 0.269 | 0.953 | 0.444 | 0.468 | 0.595 |
| 0.213 | 0.293 | 0.951 | 0.391 | 0.441 | 0.567 |
| 0.052 | 0.318 | 0.951 | 0.251 | 0.344 | 0.468 |
| 0.423 | 0.171 | 0.953 | 0.411 | 0.408 | 0.550 |
| 0.425 | 0.220 | 0.952 | 0.447 | 0.451 | 0.585 |
| 0.284 | 0.269 | 0.951 | 0.418 | 0.451 | 0.579 |
| 0.160 | 0.293 | 0.950 | 0.355 | 0.416 | 0.542 |
| 0.001 | 0.318 | 0.950 | 0.068 | 0.156 | 0.259 |
| 0.591 | 0.649 | 0.995 | 0.726 | 0.756 | 0.827 |
| 0.580 | 0.766 | 0.994 | 0.762 | 0.805 | 0.860 |
| 0.427 | 0.883 | 0.992 | 0.721 | 0.800 | 0.850 |
| 0.297 | 0.942 | 0.992 | 0.653 | 0.764 | 0.818 |
| 0.132 | 1.000 | 0.991 | 0.508 | 0.665 | 0.735 |
| 0.528 | 0.649 | 0.993 | 0.699 | 0.739 | 0.813 |
| 0.522 | 0.766 | 0.992 | 0.735 | 0.787 | 0.845 |
| 0.373 | 0.883 | 0.991 | 0.689 | 0.779 | 0.832 |
| 0.246 | 0.942 | 0.990 | 0.613 | 0.735 | 0.794 |
| 0.082 | 1.000 | 0.989 | 0.434 | 0.604 | 0.683 |
| 0.951 | 0 | 0.052 | 0 | 0 | 0 |
| 0.942 | 0.025 | 0.031 | 0.091 | 0.057 | 0.050 |
| 0.882 | 0.049 | 0.022 | 0.099 | 0.064 | 0.047 |
| 0.832 | 0.061 | 0.022 | 0.104 | 0.069 | 0.049 |
| 0.770 | 0.074 | 0.024 | 0.112 | 0.076 | 0.054 |
| 0.943 | 0 | 0.030 | 0 | 0 | 0 |
| 0.923 | 0.025 | 0.018 | 0.075 | 0.046 | 0.036 |
| 0.850 | 0.049 | 0.016 | 0.088 | 0.056 | 0.039 |
| 0.795 | 0.061 | 0.020 | 0.100 | 0.066 | 0.046 |
| 0.727 | 0.074 | 0.026 | 0.113 | 0.077 | 0.056 |
| 0.991 | 0.240 | 0.603 | 0.524 | 0.461 | 0.517 |
| 0.985 | 0.298 | 0.583 | 0.556 | 0.496 | 0.534 |
| 0.927 | 0.357 | 0.573 | 0.575 | 0.523 | 0.548 |
| 0.879 | 0.386 | 0.572 | 0.580 | 0.533 | 0.553 |
| 0.818 | 0.415 | 0.575 | 0.581 | 0.542 | 0.559 |
| 0.988 | 0.240 | 0.610 | 0.526 | 0.463 | 0.520 |
| 0.970 | 0.298 | 0.597 | 0.558 | 0.499 | 0.540 |
| 0.900 | 0.357 | 0.595 | 0.577 | 0.527 | 0.558 |
| 0.847 | 0.386 | 0.598 | 0.581 | 0.539 | 0.565 |
| 0.780 | 0.415 | 0.605 | 0.582 | 0.548 | 0.572 |
| 0.951 | 0.171 | 0.500 | 0.434 | 0.371 | 0.422 |
| 0.942 | 0.220 | 0.485 | 0.466 | 0.404 | 0.440 |
| 0.882 | 0.269 | 0.481 | 0.486 | 0.431 | 0.456 |
| 0.832 | 0.293 | 0.484 | 0.491 | 0.442 | 0.464 |
| 0.770 | 0.318 | 0.489 | 0.494 | 0.451 | 0.471 |
| 0.943 | 0.171 | 0.467 | 0.423 | 0.360 | 0.404 |
| 0.923 | 0.220 | 0.460 | 0.455 | 0.394 | 0.425 |
| 0.850 | 0.269 | 0.465 | 0.475 | 0.422 | 0.444 |
| 0.795 | 0.293 | 0.471 | 0.480 | 0.433 | 0.453 |
| 0.727 | 0.318 | 0.480 | 0.481 | 0.443 | 0.461 |
| 0.991 | 0.649 | 0.792 | 0.799 | 0.765 | 0.780 |
| 0.985 | 0.766 | 0.776 | 0.837 | 0.810 | 0.802 |
| 0.927 | 0.883 | 0.772 | 0.859 | 0.845 | 0.821 |
| 0.879 | 0.942 | 0.774 | 0.863 | 0.859 | 0.829 |
| 0.818 | 1.000 | 0.779 | 0.861 | 0.870 | 0.836 |
| 0.988 | 0.649 | 0.787 | 0.797 | 0.763 | 0.776 |
| 0.970 | 0.766 | 0.779 | 0.834 | 0.809 | 0.802 |
| 0.900 | 0.883 | 0.783 | 0.854 | 0.845 | 0.824 |
| 0.847 | 0.942 | 0.789 | 0.858 | 0.860 | 0.834 |
| 0.780 | 1.000 | 0.798 | 0.854 | 0.870 | 0.842 |
| Weights (%) | Cutting Condition | Cross-Feed (mm/pass) | Workpiece Velocity (m/min) | Wheel Velocity (m/s) | Depth of Cut (mm) | Temp. (°C) | MRR (mm3/min) | Total Cost (BDT) | Overall Desirability |
|---|---|---|---|---|---|---|---|---|---|
| 33.33:33.33:33.33 (Equal) | Wet | 6 | 12 | 15 | 0.095 | 140.854 | 6840 | 8.36 | 0.863 |
| 20:40:40 | Wet | 6 | 12 | 15 | 0.100 | 143.945 | 7200 | 7.77 | 0.870 (tied) |
| 6 | 12 | 25 | 0.100 | 150.119 | 7200 | 6.32 | |||
| 15:25:60 | Dry | 6 | 12 | 15 | 0.080 | 204.565 | 5760 | 1.01 | 0.860 |
| 100:0:0 (temperature only) | Wet | 3 | 12 | 15 | 0.070 | 109.785 | 2520 | 12.24 | 0.991 |
| 0:0:100 (total cost only) | Dry | 6 | 12 | 15 | 0.070 | 191.799 | 5040 | 1.08 | 0.995 |
| Schemes | Cutting Condition | Optimum Cutting Parameters | Optimum Process Parameters | Absolute Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Experimental Values | Predicted Values | ||||||||||
| Weights (%) | Temp. (°C) | Total Cost (BDT) | Overall Desirability | Temp. (°C) | Total Cost (BDT) | Overall Desirability | Temp. (°C) | Total Cost (BDT) | Overall Desirability | ||
| 33.33:33.33: 33.33 (Equal) | Wet | (fb, vw, vs, ap) = (6, 12, 15, 0.095) | 140.854 | 8.36 | 0.863 | 134.555 | 7.366 | 0.844 | 4.47 | 7.37 | 2.2 |
| 20:40:40 | Wet | (fb, vw, vs, ap) = (6, 12, 15, 0.1) | 143.945 | 7.77 | 0.870 (tied) | 146.954 | 7.226 | 0.864 | 2.08 | 7.23 | 0.69 |
| (fb, vw, vs, ap) = (6, 12, 25, 0.1) | 150.119 | 6.32 | 154.771 | 6.69 | 0.867 | 3.099 | 5.85 | 0.35 | |||
| 15:25:60 | Dry | (fb, vw, vs, ap) = (6, 12, 15, 0.08) | 204.565 | 1.01 | 0.860 | 195.43 | 1.09 | 0.852 | 4.46 | 7.9 | 0.93 |
| 100:0:0 (temperature only) | Wet | (fb, vw, vs, ap) = (3, 12, 15, 0.07) | 109.785 | 12.24 | 0.991 | 111.69 | 12.25 | 0.989 | 1.73 | 0.16 | 0.20 |
| 0:0:100 (total cost only) | Dry | (fb, vw, vs, ap) = (6, 12, 15, 0.07) | 191.799 | 1.08 | 0.995 | 193.33 | 1.08 | 0.994 | 0.80 | 0 | 0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, R.; Ghosh, S.K.; Kaisar, T.I.; Ahmed, T.; Hossain, S.; Aslam, M.; Kaseem, M.; Rahman, M.M. Multi-Response Optimization of Surface Grinding Process Parameters of AISI 4140 Alloy Steel Using Response Surface Methodology and Desirability Function under Dry and Wet Conditions. Coatings 2022, 12, 104. https://doi.org/10.3390/coatings12010104
Roy R, Ghosh SK, Kaisar TI, Ahmed T, Hossain S, Aslam M, Kaseem M, Rahman MM. Multi-Response Optimization of Surface Grinding Process Parameters of AISI 4140 Alloy Steel Using Response Surface Methodology and Desirability Function under Dry and Wet Conditions. Coatings. 2022; 12(1):104. https://doi.org/10.3390/coatings12010104
Chicago/Turabian StyleRoy, Rakesh, Sourav Kumar Ghosh, Tanvir Ibna Kaisar, Tazim Ahmed, Shakhawat Hossain, Muhammad Aslam, Mosab Kaseem, and Md Mahfuzur Rahman. 2022. "Multi-Response Optimization of Surface Grinding Process Parameters of AISI 4140 Alloy Steel Using Response Surface Methodology and Desirability Function under Dry and Wet Conditions" Coatings 12, no. 1: 104. https://doi.org/10.3390/coatings12010104
APA StyleRoy, R., Ghosh, S. K., Kaisar, T. I., Ahmed, T., Hossain, S., Aslam, M., Kaseem, M., & Rahman, M. M. (2022). Multi-Response Optimization of Surface Grinding Process Parameters of AISI 4140 Alloy Steel Using Response Surface Methodology and Desirability Function under Dry and Wet Conditions. Coatings, 12(1), 104. https://doi.org/10.3390/coatings12010104