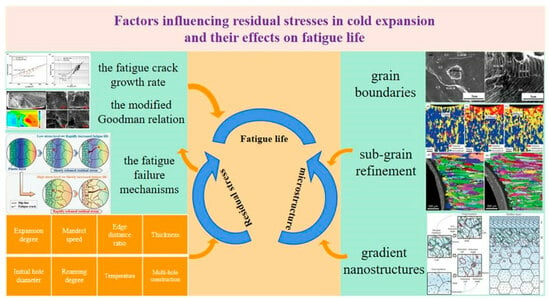
Factors Influencing Residual Stresses in Cold Expansion and Their Effects on Fatigue Life—A Review
Abstract
:1. Introduction
2. Measurement Methods for Residual Stresses
2.1. Experimental Measurement Methods
2.2. Numerical Simulation Method
3. Factors Influencing Residual Stresses
3.1. Expansion Degree
| Material | The Expansion Degree | Fatigue Life Improvement | Ref. |
|---|---|---|---|
| D16chT | 2.7% | 6.6 times | 2022 [11] |
| 2A12T4 | 6% | 6 times | 2008 [3] |
| AA6061-T6 | 4% | 2.47 times | 2017 [10] |
| 7075-T6 | 4% | 9 times | 2023 [45] |
| 7050-T7451 | 4% | 3 times | 2022 [33] |
| TC4 | 4% | 1.7–2.2 times | 2015 [39] |
| Railway steel | 4% | 2 times | 2022 [46] |
| AZ31B | 6% | 4 times | 2023 [47] |
3.2. Mandrel Speed
3.3. Edge Distance Ratio
3.4. Thickness
3.5. Initial Hole Diameter
3.6. Reaming
3.7. Temperature
3.8. Multi-Hole Construction
4. The Effect of Cold Expansion on Fatigue Life
4.1. Effect of Residual Compressive Stress on Fatigue Life
4.2. The Effect of Microstructure on Fatigue Life
5. Challenges and Future Trends
5.1. Application of Finite Element Simulation
5.2. Development of New Materials
| Mass (%) | Various Commercially Available Aircraft | |||||
|---|---|---|---|---|---|---|
| B747 | B757 | B767 | B777 | B787 | A300B4 | |
| Aluminum | 81 | 78 | 80 | 70 | 20 | 77 |
| Steel | 13 | 12 | 14 | 11 | 10 | 12 |
| Titanium | 4 | 6 | 2 | 7 | 15 | 4 |
| Composite | 1 | 3 | 3 | 11 | 50 | 4 |
| Misc. | 1 | 1 | 1 | 1 | 5 | 3 |
5.3. Application of New Processes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, D.Y.; Ma, S.D.; Jing, T.; Wang, Y.D.; Wang, L.S.; Kang, J.; Wang, Q.; Wang, W.; Li, T.; Su, R. Revealing the mechanism of grain refinement and anti Si-poisoning induced by (Nb, Ti) B2 with a sandwich-like structure. Acta Mater. 2021, 219, 117265. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Abazadeh, B.; Vogwetl, J. The effect of bolt clamping force on the fracture strength and the stress intensity factor of a plate containing a fastener hole with edge cracks. Eng. Fail. Anal. 2009, 16, 242–253. [Google Scholar] [CrossRef]
- Lou, J.; Shao, X.J.; Lou, Y.S.; Yue, Z.F. Effect of cold expansion on fatigue performance of open holes. Mater. Sci. Eng. A 2008, 477, 271–276. [Google Scholar] [CrossRef]
- Liu, J.; Xu, H.L.; Zhai, H.B.; Yue, Z.F. Effect of detail design on fatigue performance of fastener hole. Mater. Des. 2010, 31, 976–980. [Google Scholar] [CrossRef]
- Liu, J.; Yue, Z.F.; Liu, Y.S. Surface finish of open holes on fatigue life. Theor. Appl. Fract. Mech. 2007, 47, 35–45. [Google Scholar] [CrossRef]
- Yan, C.L.; Liu, K.G. Theory of economic life Prediction and readability assessment of aircraft structures. Chin. J. Aeronaut. 2011, 24, 164–170. [Google Scholar] [CrossRef]
- Fu, Y.; Ge, E.; Su, H.H.; Xu, J.H.; Li, R.Z. Cold expansion technology of connection holes in aircraft structures: A review and prospect. Chin. J. Aeronaut. 2015, 28, 961–973. [Google Scholar] [CrossRef]
- Maximov, J.T.; Duncheva, G.V.; Amudjev, I.M. A novel method and tool which enhance the fatigue life of structural components with fastener holes. Eng. Fail. Anal. 2013, 31, 132–143. [Google Scholar] [CrossRef]
- Tan, L.; Zhang, D.H.; Yao, C.F.; Wu, D.X.; Zhang, J.Y. Evolution and empirical modeling of compressive residual stress profile after milling, polishing and shot peening for TC17 alloy. J. Manuf. Process. 2017, 26, 155–165. [Google Scholar] [CrossRef]
- Wang, Y.L.; Zhu, Y.L.; Hou, S.; Sun, H.X.; Zhou, Y. Investigation on fatigue performance of cold expansion holes of 6061-T6 aluminum alloy. Int. J. Fatigue 2017, 95, 216–228. [Google Scholar] [CrossRef]
- Yasniy, P.; Okipnyi, I.; Dyvdyk, O.; Rudawska, A.; Senchyshyn, V. Residual lifetime of the plates with preexisting crack near cold expanded hole. Procedia Struct. Integr. 2022, 36, 197–202. [Google Scholar] [CrossRef]
- Leon, A. Benefits of split mandrel coldworking. Int. J. Fatigue 1998, 20, 1–10. [Google Scholar] [CrossRef]
- Reid, L. Hole cold expansion-The fatigue mitigation game changer of the past 50 years. Adv. Mater. Res. 2014, 891, 679–684. [Google Scholar] [CrossRef]
- McNeill, W.A.; Heston, A.W. Coldworking fastener holes-theoretical analysis, methods of coldworking, experimental results. In Proceedings of the ASM Conference on Residual Stresses in Design, Process and Materials Selection, Cincinnati, OH, USA, 27–29 April 1987. [Google Scholar]
- Chakherlou, T.N.; Taghizadeh, H.; Aghdam, A.B. Experimental and numerical comparison of cold expansion and interference fit methods in improving fatigue life of holed plate in double shear lap joints. Aerosp. Sci. Technol. 2013, 29, 351–362. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, W.P.; Shen, F.; Meng, Q.C.; Xu, Y.M. Numerical simulations of the fatigue damage evolution at a fastener hole treated by cold expansion or with interference fit pin. Int. J. Mech. Sci. 2016, 107, 188–200. [Google Scholar] [CrossRef]
- Yao, S.L.; Lei, X.L.; Wang, R.Z.; He, C.Y.; Zhang, X.C.; Tu, S.T. A novel cold expansion process for improving the surface integrity and fatigue life of small-deep holes in Inconel 718 superalloys. Int. J. Fatigue 2022, 154, 106544. [Google Scholar] [CrossRef]
- Amrouche, A.; Mesmacque, G.; Garcia, S.; Talha, A. Cold expansion effect on the initiation and the propagation of the fatigue crack. Int. J. Fatigue 2003, 25, 949–954. [Google Scholar] [CrossRef]
- Pasta, S. Fatigue crack propagation from a cold-worked hole. Eng. Fract. Mech. 2007, 74, 1525–1538. [Google Scholar] [CrossRef]
- Hou, S.; Zhu, Y.L.; Cai, Z.H.; Wang, Y.L.; Ni, Y.H.; Du, X.K. Effect of hold cold expansion on fatigue performance of corroded 7B04-T6 aluminium alloy. Int. J. Fatigue 2019, 126, 210–220. [Google Scholar]
- Chakherlou, T.N.; Shahriary, P.; Akbari, A. Experimental and numerical investigation on the fretting fatigue behavior of cold expanded Al-alloy 2024-T3 plates. Eng. Fail. Anal. 2021, 123, 105324. [Google Scholar] [CrossRef]
- Belasset, M.; Pineault, J.; Brauss, M. Comparison and evaluation of residual stress measurement techniques, a technical and economical study. In Proceedings of the SEM Annual Conference and Exposition on Experimental and Applied Mechanics, Saint Louis, MO, USA, 4–7 June 2006; pp. 756–762. [Google Scholar]
- Guo, J.; Fu, H.Y.; Pan, B.; Kang, R.K. Recent progress of residual stress measurement methods: A Review. Chin. J. Aeronaut. 2021, 34, 54–78. [Google Scholar] [CrossRef]
- Gholizadeh, S. A review of non-destructive testing methods of composite materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- ASTM E837; Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. ASTM: West Conshohocken, PA, USA, 2008.
- Sakharova, N.A.; Prates, P.A.; Oliveira, M.C.; Fernandes, J.V.; Antunes, J.M. A simple method for estimation of residual stresses by depth-sensing indentation. Strain 2012, 48, 75–87. [Google Scholar] [CrossRef]
- Ribeiro, R.L.; Olson, M.; Hill, M.R. Measurement-driven, model-based estimation of residual stress and its effects on fatigue crack growth. Part 1: Validation of an eigenstrain model. Int. J. Fatigue 2009, 163, 107070. [Google Scholar] [CrossRef]
- Ribeiro, R.L.; Hill, M.R. Measurement-driven, model-based estimation of residual stress and its effects on fatigue crack growth. Part 2: Fatigue crack growth testing and modeling. Int. J. Fatigue 2022, 163, 107044. [Google Scholar] [CrossRef]
- Gao, Y.K.; Wu, X.R. Experimental investigation and fatigue life prediction for 7475-T7351 aluminum alloy with and without shot peening-induced residual stresses. Acta Mater. 2011, 59, 3737–3747. [Google Scholar] [CrossRef]
- De Matos, P.F.P.; Moreira, P.M.G.P.; Pina, J.C.P.; Dias, A.M.; De Castro, P.M.S.T. Residual stress effect on fatigue striation spacing in a cold-worked rivet hole. Theor. Appl. Fract. Mech. 2004, 42, 139–148. [Google Scholar] [CrossRef]
- Lacarac, V.D.; Garcia-Granada, A.A.; Smith, D.J.; Pavier, M.J. Prediction of the growth rate for fatigue cracks emanating from cold expanded holes. Int. J. Fatigue 2004, 26, 585–598. [Google Scholar] [CrossRef]
- Webster, G.A.; Ezeilo, A.N. Residual stress distributions and their influence on fatigue lifetimes. Int. J. Fatigue 2001, 23, S375–S383. [Google Scholar] [CrossRef]
- Li, Q.; Xue, Q.C.; Hu, Q.S.; Song, T.; Wang, Y.H.; Li, S.Y. Cold expansion strengthening of 7050 aluminum alloy hole: Structure, residual stress, and fatigue life. Int. J. Aerospace Eng. 2022, 2022, 17. [Google Scholar] [CrossRef]
- Matvienko, Y.; Pisarev, V.; Eteonsky, S. Low-cycle fatigue damage accumulation near the cold-expanded hole by crack compliance data. Int. J. Fatigue 2022, 155, 106590. [Google Scholar] [CrossRef]
- Veticheti, D.; Nagy, P.B.; Hassan, W. Residual stress and cold work assessment in shot-peened IN718 using a dual-mode electromagnetic technique. NDT E Int. 2021, 121, 102463. [Google Scholar] [CrossRef]
- Schajer, G.S.; Prime, M.B.; Withers, P.J. Why is it so challenging to measure residual stresses? Exp. Mech. 2022, 62, 1521–1530. [Google Scholar] [CrossRef]
- Babu, N.C.M.; Jagadish, T.; Ramachandra, K.; Sridhara, S.N. A simplified 3-D finite element simulation of cold expansion of a circular hole to capture through thickness variation of residual stresses. Eng. Fail. Anal. 2008, 15, 339–348. [Google Scholar] [CrossRef]
- Kumar, S.A.; Babu, N.C.M. Influence of induced residual stresses on fatigue performance of cold expanded fastener holes. Mater. Today Proc. 2017, 4, 2397–2402. [Google Scholar] [CrossRef]
- Yuan, X.; Yue, Z.F.; Wen, S.F.; Li, L.; Feng, T. Numerical and experimental investigation of the cold expansion process with split sleeve in titanium alloy TC4. Int. J. Fatigue 2015, 77, 78–85. [Google Scholar] [CrossRef]
- Peretzki, E.; Lehmann, T.; Ihlemann, J. Adaption of the hole drilling method for residual stress analysis inside plastic parts. Mater. Today Proc. 2022, 62, 2523–2527. [Google Scholar] [CrossRef]
- Ding, Z.S.; Sun, G.X.; Guo, M.X.; Jiang, X.H.; Li, B.Z.; Liang, S.Y. Effect of phase transition on micro-grinding-induced residual stress. J. Mater. Process Tech. 2019, 281, 116647. [Google Scholar] [CrossRef]
- Liu, Y.S.; Shao, X.J.; Liu, J.; Yue, Z.F. Finite element method and experimental investigation on the residual stress fields and fatigue performance of cold expansion hole. Mater. Des. 2010, 31, 1208–1215. [Google Scholar]
- Kumar, S.A.; Bhattacharya, A.; Babu, N.C.M. Fatigue crack growth life prediction around cold expanded hole using finite. Procedia Mater. Sci. 2014, 5, 316–325. [Google Scholar] [CrossRef]
- Ghfiri, R.; Amrouche, A.; Imad, A.; Mesmacque, G. Fatigue life estimation after crack repair in 6005 A-T6 aluminium alloy using the cold expansion hole technology. Fatigue Fract. Eng. M 2000, 23, 911–916. [Google Scholar] [CrossRef]
- Wang, C.G.; Zou, F.; Zhou, E.T.; Fan, Z.L.; Ge, E.D.; An, Q.L.; Ming, W.W.; Chen, M. Effect of split sleeve cold expansion on microstructure and fatigue performance of 7075-T6 aluminum alloy holes. Int. J. Fatigue 2023, 167, 107339. [Google Scholar] [CrossRef]
- Pucillo, G.P.; De Vita, G.; Fedeli, E. Fatigue crack growth rate dependency on cold expansion degree in railway steel. Procedia Struct. Integr. 2022, 39, 700–710. [Google Scholar] [CrossRef]
- Faghih, S.; Shaha, S.K.; Behravesh, S.B.; Jahed, H. Split sleeve cold expansion of AZ31B sheet: Microstructure, texture and residual stress. Mater. Des. 2020, 186, 108213. [Google Scholar] [CrossRef]
- Farhangdoost, K.H.; Hosseini, A. The Effect of mandrel speed upon the residual stress distribution around cold expanded hole. Procedia Eng. 2011, 10, 2184–2189. [Google Scholar] [CrossRef]
- Farhangdoost, K.H.; Hosseini, A. Finite element modeling of mandrel speed in cold expansion process. Int. J. Struct. Integr. 2012, 3, 441–456. [Google Scholar] [CrossRef]
- Liu, J.; Wu, H.G.; Yang, J.J.; Yue, Z.F. Effect of edge distance ratio on residual stresses induced by cold expansion and fatigue life of TC4 plates. Eng. Fract. Mech. 2013, 109, 130–137. [Google Scholar] [CrossRef]
- Restis, J.; Reid, L. FTI Process Specification 8101D: Cold Expansion of Holes Using the Standard Split Sleeve System and Countersink Cold Expansion; Fatigue Technology Inc.: Seattle, WA, USA, 2002. [Google Scholar]
- Ayatollahi, M.R.; Nik, M.A. Edge distance effects on residual stress distribution around a cold expanded hole in Al 2024 alloy. Comput. Mater. Sci. 2009, 45, 1134–1141. [Google Scholar] [CrossRef]
- De Matos, P.F.P.; Moreira, P.M.G.P.; Camanho, P.P.; De Castro, P.M.S.T. Numerical simulation of cold working of rivet holes. Finite Elem. Anal. Des. 2005, 41, 989–1007. [Google Scholar] [CrossRef]
- Stuart, D.H.; Hill, M.R.; Newman, J.J. Correlation of one-dimensional fatigue crack growth at cold-expanded holes using linear fracture mechanics and superposition. Eng. Fract. Mech. 2011, 7, 1389–1406. [Google Scholar] [CrossRef]
- Ozdemir, A.T.; Hermann, R. Effect of expansion technique and plate thickness on near-hole residual stresses and fatigue life of cold expanded holes. J. Mater. Sci. 1999, 34, 1243–1252. [Google Scholar] [CrossRef]
- Yasniy, P.; Glado, S.; Lashii, V. Lifetime of aircraft alloy plates with cold expanded holes. Int. J. Fatigue 2017, 104, 112–119. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, Q.Y.; Liu, F.L. Effect of strengthened hole on residual stress of 7050 aluminum alloy. Aeronaut. Manuf. Tech. 2016, 59, 80–82. (In Chinese) [Google Scholar]
- Liu, K.Y.; Yang, X.S.; Li, Z.; Li, M.; Zhu, W.J. Numerical investigation of the effect of hole reaming on fatigue life by cold expansion. Trans. Can. Soc. Mech. Eng. 2021, 46, 400–411. [Google Scholar] [CrossRef]
- Li, K.S.; Wang, R.Z.; Zhang, X.C.; Yao, S.L.; Cheng, L.Y.; Lei, X.L.; Tu, S.T. Process-performance-prediction integration for fatigue life improvement technologies: An implementation in cold expansion of hole structures. Int. J. Fatigue 2023, 170, 107507. [Google Scholar] [CrossRef]
- Lacarac, V.D.; Smith, D.J.; Pavier, M.J. The effect of cold expansion on fatigue crack growth from open holes at room and high temperature. Int. J. Fatigue 2001, 23, S161–S170. [Google Scholar] [CrossRef]
- Aghdam, A.B.; Chakherlou, T.N.; Saeedi, K. An FE analysis for assessing the effect of short-term exposure to elevated temperature on residual stresses around cold expanded fastener holes in aluminum alloy 7075-T6. Mater. Des. 2010, 31, 500–507. [Google Scholar] [CrossRef]
- Minguez, J.M.; Vogwetl, J. Fatigue life of an aerospace aluminium alloy subjected to cold expansion and a cyclic temperature regime. Eng. Fail. Anal. 2006, 12, 997–1004. [Google Scholar] [CrossRef]
- Clark, D.A.; Johnson, W.S. Temperature effects on fatigue performance of cold expanded holes in 7050-T7451 aluminum alloy. Int. J. Fatigue 2003, 25, 159–165. [Google Scholar] [CrossRef]
- Wang, X.; Xu, C.; Chen, X.; Hu, D.Y.; Hu, B.; Hu, R.G.; Gu, Y.X.; Tang, Z.H. Effect of cold expansion on high-temperature low-cycle fatigue performance of the nickel-based superalloy hole structure. Int. J. Fatigue 2021, 15, 106377. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Aghdam, A.B.; Akbari, A.; Saeedi, K. Analysis of cold expanded fastener holes subjected to short time creep: Finite element modelling and fatigue tests. Mater. Des. 2010, 31, 2858–2866. [Google Scholar] [CrossRef]
- Chakherlou, T.N.; Aghdam, A.B. An experimental investigation on the effect of short time exposure to elevated temperature on fatigue life of cold expanded fastener holes. Mater. Des. 2008, 29, 1504–1511. [Google Scholar] [CrossRef]
- Kim, C.; Kim, D.J.; Seok, C.S.; Yang, W.H. Finite element analysis of the residual stress by cold expansion method under the influence of adjacent holes. J. Mater. Process. Technol. 2004, 153–154, 986–991. [Google Scholar] [CrossRef]
- Kumar, S.A.; Babu, N.C.M. Effect of proximity hole on induced residual Stresses during cold expansion of adjacent holes. Mater. Today Proc. 2018, 5, 5709–5715. [Google Scholar] [CrossRef]
- Seifi, R. Total fatigue lives, crack growth paths and cycles in cold expanded adjacent holes. Int. J. Fatigue 2018, 113, 69–77. [Google Scholar] [CrossRef]
- Moreira, P.M.G.P.; De Matos, P.F.P.; Pinho, S.T.; Pastrama, S.D.; Camanho, P.P.; De Castro, P.M.S.T. The residual stress intensity factors for cold worked cracked holes: A technical note. Fatigue Fract. Eng. M 2004, 27, 879–886. [Google Scholar] [CrossRef]
- Pucillo, G.P. The effects of the cold expansion degree on fatigue crack growth rate in rail steel. Int. J. Fatigue 2022, 164, 107130. [Google Scholar] [CrossRef]
- Murakami, Y.; Keer, L.M. Stress Intensity Factors Handbook; British Energy Generation Limited: London, UK, 1993; Volume 3. [Google Scholar]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook; ASME Press: New York, NY, USA, 2000. [Google Scholar]
- Yan, W.Z.; Wang, X.S.; Gao, H.S.; Yue, Z.F. Effect of split sleeve cold expansion on cracking behaviors of titanium alloy TC4 holes. Eng. Fract. Mech. 2012, 88, 79–89. [Google Scholar] [CrossRef]
- De Matos, P.F.P.; McEvily, A.J.; Moreira, P.M.G.P.; De Castro, P.M.S.T. Analysis of the effect of cold-working of rivet holes on the fatigue life of an aluminum alloy. Int. J. Fatigue 2007, 29, 575–586. [Google Scholar] [CrossRef]
- Chandawanich, N.; Sharpe, J.W. An experimental study of fatigue crack initiation and growth from coldworked holes. Eng. Frac. Mech. 1979, 11, 609–620. [Google Scholar] [CrossRef]
- Kattoura, M.; Telang, A.; Mannava, S.R.; Qian, D.; Vasudevan, V.K. Effect of ultrasonic nanocrystal surface modification on residual stress, microstructure and fatigue behavior of ATI 718Plus alloy. Mater. Sci. Eng. A 2018, 711, 364–377. [Google Scholar] [CrossRef]
- Reddy, G.V.P.; Robertson, C.; Depres, C.; Fivel, M. Effect of grain disorientation on early fatigue crack propagation in face-centred-cubic polycrystals: A three-dimensional dislocation dynamics investigation. Acta Mater. 2013, 61, 5300–5310. [Google Scholar] [CrossRef]
- Schaef, W.; Marx, M.; Vehoff, H.; Heckl, A.; Randelzhofer, P. A 3-D view on the mechanisms of short fatigue cracks interacting with grain boundaries. Acta Mater. 2011, 59, 1849–1861. [Google Scholar] [CrossRef]
- Jamali, A.; Ma, A.X.; Lorca, J.L. Influence of grain size and grain boundary misorientation on the fatigue crack initiation mechanisms of textured AZ31 Mg alloy. Sripta Mater. 2022, 207, 114304. [Google Scholar] [CrossRef]
- Su, R.; Li, J.Y.; Liu, W.G.; Xu, C.Z.; Gao, L.J.; Liang, X.Z.; Wu, D.Y.; Huang, X.; Dong, H.C.; Ma, H.K. Investigation on fatigue failure of split-sleeve cold expansion holes of 7075-T651 aluminum alloy. Mater. Today Commun. 2023, 35, 106290. [Google Scholar] [CrossRef]
- Tandon, R.; Mehta, K.K.; Manna, R.; Mandal, R.K. Effect of tensile straining on the precipitation and dislocation behavior of AA7075T7352 aluminum alloy. J. Alloy. Compd. 2022, 904, 163942. [Google Scholar] [CrossRef]
- Li, X.; Sun, B.H.; Guan, B.; Jia, Y.F.; Gong, C.Y.; Zhang, X.C.; Tu, S.T. Elucidating the effect of gradient structure on strengthening mechanisms and fatigue behavior of pure titanium. Int. J. Fatigue 2021, 146, 106142. [Google Scholar] [CrossRef]
- Chen, D.M.; Liu, J.Y.; Chen, D.H.; Li, R.W.; Ma, C.; Wang, M.; Dong, P.; Lang, D.M.; Hu, Y.; Liu, K.Z. Influence of ultrasonic surface rolling process on surface characteristics and micro-mechanical properties of uranium. Mater. Chem. Phys. 2022, 279, 125741. [Google Scholar] [CrossRef]
- Sanni, O.; Ren, J.; Jen, T.C. Agro-industrial wastes as corrosion inhibitor for 2024-T3 aluminum alloy in hydrochloric acid medium. Results Eng. 2022, 16, 100676. [Google Scholar] [CrossRef]
- Dursun, T.; Soutis, C. Recent developments in advanced aircraft aluminium alloys. Mater. Des. 2014, 56, 862–871. [Google Scholar] [CrossRef]
- Sharma, J.; Nayak, C.; Chauhan, P.S.; Kumar, R. Studies and scientific research analysis of aluminium (Al7075) metal matrix composite surface morphology. Mater. Today Process. 2023. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Lu, Y.X.; Sun, L.G.; Huang, S.; Mei, L.B.; Zhu, M.L.; Xuan, F.Z. Effect of microstructure on fatigue resistance of Inconel 740H and Haynes 282 nickel-based alloys at high temperature. Mater. Charact. 2023, 203, 113095. [Google Scholar] [CrossRef]
- Mao, Z.Z.; Zhu, Y.B.; Zhao, Y.; Xie, H.M.; Yang, Y.H.; Zhou, Y.Z.; Huang, X.F.; Liu, Z.W. High-cycle fatigue failure behavior of nickel-based single crystal alloys with different deviation angles in a high-temperature environment. Mater. Charact. 2023, 203, 112118. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Umer, R.; Khan, K.A. Review of recent trends and developments in aluminium 7075 alloys and metal matrix composites (MMCs) for aircraft applications. Results Eng. 2023, 20, 101372. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Fu, J.K.; Cao, Q.L.; Lai, Z.P.; Xiong, Q.; Han, X.T.; Li, L. Electromagnetic cold-expansion process for circular holes in aluminum alloy sheets. J. Mater. Process. Technol. 2017, 248, 49–55. [Google Scholar] [CrossRef]
- Zheng, G.; Cao, Z.Q.; Zuo, Y.J. A dynamic cold expansion method to improve fatigue performance of holed structures based on electromagnetic load. Int. J. Fatigue 2021, 148, 106253. [Google Scholar] [CrossRef]
- Geng, H.H.; Xu, X.F.; Lai, Z.P.; Cao, Q.L.; Li, L. A novel non-contacting single-coil electromagnetic hole expansion process to improve the fatigue performance of hole component. Int. J. Fatigue 2022, 162, 106924. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, P.; Liu, S.; Lei, X.L.; Wang, R.Z.; Zhang, X.C.; Tu, S.T. A novel hole cold-expansion method and its effect on surface integrity of nickel-based superalloy. J. Mater. Sci. Tech. 2020, 59, 129–137. [Google Scholar] [CrossRef]
- Shim, J.Y.; Kang, B.Y.; Yun, T.J.; Lee, B.R.; Kim, I.S. The present situation of the research and development of the electromagnetic pulse technology. Mater. Today Proc. 2020, 22, 1958–1966. [Google Scholar] [CrossRef]
- Li, S.J.; Wei, B.W.; Xu, J.J.; Xu, G.M.; Li, Y.; Wang, Z.D. High solid-solution strengthening mechanism of a novel aluminum-lithium alloy fabricated by electromagnetic near-net shape technology. Mater. Sci. Eng. A 2022, 829, 142148. [Google Scholar] [CrossRef]
- Karim, S.S.; Murtaza, Z.; Farrukh, S.; Umer, M.A.; Ali, S.S.; Younas, M.; Mubashir, M.; Saqib, S.; Ayoub, M.; Bokhari, A.; et al. Future advances and challenges of nanomaterial-based technologies for electromagnetic interference-based technologies: A review. Environ. Res. 2022, 205, 112402. [Google Scholar] [CrossRef] [PubMed]
















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, R.; Huang, L.; Xu, C.; He, P.; Wang, X.; Yang, B.; Wu, D.; Wang, Q.; Dong, H.; Ma, H. Factors Influencing Residual Stresses in Cold Expansion and Their Effects on Fatigue Life—A Review. Coatings 2023, 13, 2037. https://doi.org/10.3390/coatings13122037
Su R, Huang L, Xu C, He P, Wang X, Yang B, Wu D, Wang Q, Dong H, Ma H. Factors Influencing Residual Stresses in Cold Expansion and Their Effects on Fatigue Life—A Review. Coatings. 2023; 13(12):2037. https://doi.org/10.3390/coatings13122037
Chicago/Turabian StyleSu, Ru, Lei Huang, Changzhou Xu, Peng He, Xiaoliang Wang, Baolin Yang, Dayong Wu, Qian Wang, Huicong Dong, and Haikun Ma. 2023. "Factors Influencing Residual Stresses in Cold Expansion and Their Effects on Fatigue Life—A Review" Coatings 13, no. 12: 2037. https://doi.org/10.3390/coatings13122037
APA StyleSu, R., Huang, L., Xu, C., He, P., Wang, X., Yang, B., Wu, D., Wang, Q., Dong, H., & Ma, H. (2023). Factors Influencing Residual Stresses in Cold Expansion and Their Effects on Fatigue Life—A Review. Coatings, 13(12), 2037. https://doi.org/10.3390/coatings13122037