Numerical Study of Efficient Tm-Doped Zinc-Tellurite Fiber Lasers at 2300 nm
Abstract
:1. Introduction
2. Materials and Methods
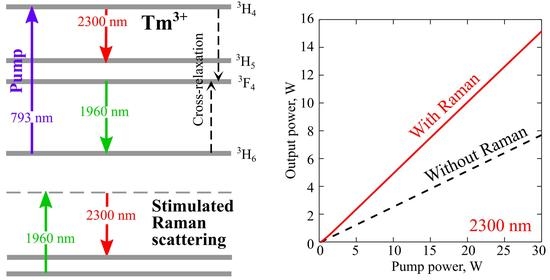
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Zhang, B.; Liu, J.; Song, Y.; Zhang, H. Recent developments in mid-infrared fiber lasers: Status and challenges. Opt. Laser Technol. 2020, 132, 106497. [Google Scholar] [CrossRef]
- Liu, H.; Yu, Y.; Song, W.; Jiang, Q.; Pang, F. Recent development of flat supercontinuum generation in specialty optical fibers. Opto-Electron. Adv. 2019, 2, 180020. [Google Scholar] [CrossRef]
- Soboń, G.; Lindberg, R.; Pasiskevicius, V.; Martynkien, T.; Sotor, J. Shot-to-shot performance analysis of an all-fiber supercontinuum source pumped at 2000 nm. J. Opt. Soc. Am. B 2018, 36, A15–A21. [Google Scholar] [CrossRef]
- Chen, L.; Liao, M.; Bi, W.; Yu, F.; Wang, T.; Gao, W.; Hu, L. Coherent Supercontinuum Generation in Step-Index Heavily Ge-Doped Silica Fibers with All Normal Dispersion. IEEE Photonics J. 2022, 14, 1–6. [Google Scholar] [CrossRef]
- Zhluktova, I.V.; Kamynin, V.A.; Korobko, D.A.; Abramov, A.S.; Fotiadi, A.A.; Sysoliatin, A.A.; Tsvetkov, V.B. Broadband Supercontinuum Generation in Dispersion Decreasing Fibers in the Spectral Range 900–2400 nm. Photonics 2022, 9, 773. [Google Scholar] [CrossRef]
- Fortin, V.; Bernier, M.; Faucher, D.; Carrier, J.; Vallée, R. 37 W fluoride glass Raman fiber laser operating at 2231 nm. Opt. Express 2012, 20, 19412–19419. [Google Scholar] [CrossRef]
- Jiao, Y.; Jia, Z.; Guo, X.; Zhao, Z.; Ohishi, Y.; Qin, W.; Qin, G. Third-order cascaded Raman shift in all-solid fluorotellurite fiber pumped at 1550 nm. Opt. Lett. 2022, 47, 690–693. [Google Scholar] [CrossRef]
- Yao, T.; Huang, L.; Zhou, P.; Lei, B.; Leng, J.; Chen, J. Power scaling on tellurite glass Raman fibre lasers for mid-infrared applications. High Power Laser Sci. Eng. 2018, 6, e24. [Google Scholar] [CrossRef] [Green Version]
- Vasilyev, S.; Moskalev, I.; Mirov, M.; Mirov, S.; Gapontsev, V. Multi-Watt mid-IR femtosecond polycrystalline Cr2+:ZnS and Cr2+:ZnSe laser amplifiers with the spectrum spanning 20–26 µm. Opt. Express 2016, 24, 1616–1623. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.; Esterowitz, L. cw diode pumped 2.3 μm fiber laser. Appl. Phys. Lett. 1989, 55, 721. [Google Scholar] [CrossRef]
- Tyazhev, A.; Starecki, F.; Cozic, S.; Loiko, P.; Guillemot, L.; Braud, A.; Joulain, F.; Tang, M.; Godin, T.; Hideur, A.; et al. Watt-level efficient 2.3 µm thulium fluoride fiber laser. Opt. Lett. 2020, 45, 5788–5791. [Google Scholar] [CrossRef]
- Falconi, M.C.; Laneve, D.; Prudenzano, F. Advances in Mid-IR Fiber Lasers: Tellurite, Fluoride and Chalcogenide. Fibers 2017, 5, 23. [Google Scholar] [CrossRef] [Green Version]
- Anashkina, E.A. Laser Sources Based on Rare-Earth Ion Doped Tellurite Glass Fibers and Microspheres. Fibers 2020, 8, 30. [Google Scholar] [CrossRef]
- Muravyev, S.V.; Anashkina, E.A.; Andrianov, A.V.; Dorofeev, V.V.; Motorin, S.E.; Koptev, M.Y.; Kim, A.V. Dual-band Tm3+-doped tellurite fiber amplifier and laser at 1.9 μm and 2.3 μm. Sci. Rep. 2018, 8, 16164. [Google Scholar] [CrossRef] [Green Version]
- Denker, B.I.; Dorofeev, V.V.; Galagan, B.I.; Koltashev, V.V.; Motorin, S.E.; Plotnichenko, V.G.; Sverchkov, S.E. A 200 mW, 2.3 µm Tm3+-doped tellurite glass fiber laser. Laser Phys. Lett. 2020, 17, 095101. [Google Scholar] [CrossRef]
- Kamynin, V.; Filatova, S.; Denker, B.; Galagan, B.; Koltashev, V.; Medvedkov, O.; Sverchkov, S.; Tsvetkov, V. Tm3+-doped tellurite fiber weak signal amplifier at a wavelength of 2.27 µm. Results Phys. 2021, 27, 104512. [Google Scholar] [CrossRef]
- Koptev, M.Y.; Anashkina, E.A.; Andrianov, A.; Muravyev, S.V.; Kim, A. Two-color optically synchronized ultrashort pulses from a Tm/Yb-co-doped fiber amplifier. Opt. Lett. 2014, 39, 2008–2011. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, C.; Wang, C.; Yang, L.; Wang, X.; Ren, G.; Li, P. High-Energy 1.96–2.4 μm Tunable Raman Soliton Generation in All-Silica-Fiber Tm-Doped Amplifier. IEEE Photonics Technol. Lett. 2023, 35, 361–364. [Google Scholar] [CrossRef]
- Dvoyrin, V.V.; Turitsyn, S.K. Generation of high-energy soliton-like pulses in 1.9–2.5 µm spectral domain. J. Phys. Photonics 2020, 2, 044005. [Google Scholar] [CrossRef]
- Kirsch, D.C.; Bednyakova, A.; Varak, P.; Honzatko, P.; Cadier, B.; Robin, T.; Fotiadi, A.; Peterka, P.; Chernysheva, M. Gain-controlled broadband tuneability in self-mode-locked Thulium-doped fibre laser. Commun. Phys. 2022, 5, 219. [Google Scholar] [CrossRef]
- Jackson, S.D.; Mossman, S. Efficiency dependence on the Tm3+ and Al3+ concentrations for Tm3+-doped silica double-clad fiber lasers. Appl. Opt. 2003, 42, 2702–2707. [Google Scholar] [CrossRef]
- Aydın, Y.O.; Fortin, V.; Maes, F.; Jobin, F.; Jackson, S.D.; Vallée, R.; Bernier, M. Diode-pumped mid-infrared fiber laser with 50% slope efficiency. Optica 2017, 4, 235–239. [Google Scholar] [CrossRef]
- Plotnichenko, V.G.; Sokolov, V.O.; Koltashev, V.V.; Dianov, E.M.; Grishin, I.A.; Churbanov, M.F. Raman band intensities of tellurite glasses. Opt. Lett. 2005, 30, 1156–1158. [Google Scholar] [CrossRef]
- Gomes, L.; Lousteau, J.; Milanese, D.; Scarpignato, G.C.; Jackson, S.D. Energy transfer and energy level decay processes in Tm3+-doped tellurite glass. J. Appl. Phys. 2012, 111, 063105. [Google Scholar] [CrossRef] [Green Version]
- Rhonehouse, D.L.; Zong, J.; Nguyen, D.; Thapa, R.; Wiersma, K.; Smith, C.; Chavez-Pirson, A. Low loss, wide transparency, robust tellurite glass fibers for mid-IR (2–5 μm) applications. SPIE Proc. 2013, 8898, 88980D. [Google Scholar] [CrossRef]
- Evrard, M.; Combes, T.; Maldonado, A.; Désévédavy, F.; Gadret, G.; Strutynski, C.; Jules, J.C.; Brachais, C.H.; Smektala, F. TeO2-ZnO-La2O3 tellurite glass purification for mid-infrared optical fibers manufacturing. Opt. Mater. Express 2021, 12, 136–152. [Google Scholar] [CrossRef]
- Svelto, O.; Hanna, D.C. Principles of Lasers; Springer: New York, NY, USA, 2010. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Jackson, S.D.; Muir, P.H. Theory and numerical simulation of nth-order cascaded Raman fiber lasers. J. Opt. Soc. Am. B 2001, 18, 1297–1306. [Google Scholar] [CrossRef]
- Sojka, L.S.; Tang, Z.; Zhu, H.; Bereś-Pawlik, E.; Furniss, D.; Seddon, A.; Benson, T.M.; Sujecki, S. Study of mid-infrared laser action in chalcogenide rare earth doped glass with Dy3+, Pr3+and Tb3+. Opt. Mater. Express 2012, 2, 1632–1640. [Google Scholar] [CrossRef] [Green Version]






| Parameter | Symbol | Value |
|---|---|---|
| Pump wavelength at 1 → 4 (3H6 → 3H4) transition | λp | 793 nm |
| Laser wavelength at 2 → 1 (3F4 → 3H6) transition | λ1 | 1960 nm |
| Laser wavelength at 4 → 3 (3H4 → 3H5) transition | λ2 | 2300 nm |
| Total lifetime of level 2 (3F4) | τ2 | 3 ms |
| Total (non-radiative) lifetime of level 3 (3H5) | τ3 | 0.13 μs |
| Non-radiative lifetime of level 4 (3H6) | τ4NR | 1.2 ms |
| Radiative lifetime of level 4 (3H6) | τ4R | 0.4 ms |
| Total lifetime of level 4 (3H6) | τ4 | 0.3 ms |
| Branching ratio from level 4 to levels 3, 2, 1 | β43 | 0.03 |
| β42 | 0.07 | |
| β41 | 0.09 | |
| Absorption cross-section at 1 → 4 transition | σ14 | 1 × 10–20 cm2 |
| Emission cross-section at 4 → 1 transition | σ41 | 1 × 10–20 cm2 |
| Absorption cross-section at 1 → 2 transition | σ12 | 0.012 × 10–20 cm2 |
| Emission cross-section at 2 → 1 transition | σ21 | 0.26 × 10–20 cm2 |
| Absorption cross-section at 3 → 4 transition | σ34 | 0.26 × 10–20 cm2 |
| Emission cross-section at 4 → 3 transition | σ43 | 0.26 × 10–20 cm2 |
| Cross-relaxation rate (for NTm = 2 × 1020 cm–3) | KCR | 5678 s–1 |
| Parameter | Symbol | Value |
|---|---|---|
| Intracavity fiber length | L | 30…300 cm |
| Tm-doped core diameter | d | 7 µm |
| Tm ion concentration in the core | NTm | 2 × 1020 cm–3 |
| Numerical aperture (core/cladding) | NA | 0.2 |
| Cladding diameter | D | 70 µm |
| Effective mode field area at λ1 = 1960 nm | Aeff1 | 51 µm2 |
| Effective mode field area at λ2 = 2300 nm | Aeff2 | 67 µm2 |
| Overlap integral (pump with doped area) | Γp | 0.01 |
| Overlap integral (1960 nm wave with doped core) | Γ1 | 0.75 |
| Overlap integral (2300 nm wave with doped core) | Γ2 | 0.6 |
| Fiber background loss at 793 nm | αp | 0.4 dB/m |
| Fiber background loss at 1960 µm | α1 | 0.3 dB/m |
| Fiber background loss at 2300 µm | α2 | 0.3 dB/m |
| Raman gain coefficient (for 2300 nm wave amplified by 1960 nm wave) | gR12 | 5 × 10–4 (W cm)–1 |
| Reflection coefficient at 1960 nm at z = 0 | R01 | 0.99 |
| Reflection coefficient at 1960 nm at z = L | RL1 | 0.99 |
| Reflection coefficient at 2300 nm at z = 0 | R02 | 0.99 |
| Reflection coefficient at 2300 nm at z = L | RL2 | 0.05…0.9 |
| Reflection coefficient at 793 nm at z = L | RLp | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anashkina, E.A.; Andrianov, A.V. Numerical Study of Efficient Tm-Doped Zinc-Tellurite Fiber Lasers at 2300 nm. Fibers 2023, 11, 57. https://doi.org/10.3390/fib11070057
Anashkina EA, Andrianov AV. Numerical Study of Efficient Tm-Doped Zinc-Tellurite Fiber Lasers at 2300 nm. Fibers. 2023; 11(7):57. https://doi.org/10.3390/fib11070057
Chicago/Turabian StyleAnashkina, Elena A., and Alexey V. Andrianov. 2023. "Numerical Study of Efficient Tm-Doped Zinc-Tellurite Fiber Lasers at 2300 nm" Fibers 11, no. 7: 57. https://doi.org/10.3390/fib11070057
APA StyleAnashkina, E. A., & Andrianov, A. V. (2023). Numerical Study of Efficient Tm-Doped Zinc-Tellurite Fiber Lasers at 2300 nm. Fibers, 11(7), 57. https://doi.org/10.3390/fib11070057