Visual Positioning System Based on 6D Object Pose Estimation Using Mobile Web

Abstract

Recently, the demand for location-based services using mobile devices in indoor spaces without a global positioning system (GPS) has increased. However, to the best of our knowledge, solutions that are fully applicable to indoor positioning and navigation and ensure real-time mobility on mobile devices, such as global navigation satellite system (GNSS) solutions, cannot achieve remarkable researches in indoor circumstances. Indoor single-shot image positioning using smartphone cameras does not require a dedicated infrastructure and offers the advantages of low price and large potential markets owing to the popularization of smartphones. However, existing methods or systems based on smartphone cameras and image algorithms encounter various limitations when implemented in indoor environments. To address this, we designed an indoor visual positioning system for mobile devices that can locate users in indoor scenes. The proposed method uses a smartphone camera to detect objects through a single image in a web environment and calculates the location of the smartphone to find users in an indoor space. The system is inexpensive because it integrates deep learning and computer vision algorithms and does not require additional infrastructure. We present a novel method of detecting 3D model objects from single-shot RGB data, estimating the 6D pose and position of the camera and correcting errors based on voxels. To this end, the popular convolutional neural network (CNN) is improved by real-time pose estimation to handle the entire 6D pose estimate the location and direction of the camera. The estimated position of the camera is addressed to a voxel to determine a stable user position. Our VPS system provides the user with indoor information in 3D AR model. The voxel address optimization approach with camera 6D position estimation using RGB images in a mobile web environment outperforms real-time performance and accuracy compared to current state-of-the-art methods using RGB depth or point cloud.

1. Introduction

Multi-usage public facilities or large crowded markets without GPS functionality fail to navigation services. Researches on indoor positioning and navigation are developing widely. Recently, machine learning and deep learning methods are applied without sensors for location recognition. However, it is difficult to maintain the quality of location-based AR service without continuous updating the built-in maps as well as constructing indoor maps [1]. Visual positioning system information, which is more innovative than navigation technology obtained using GPS information, resonates with people’s lifestyles globally. VPS allows users to use their mobile cameras to visually grasp their surroundings and directions in places where GPS services are difficult, such as indoor spaces [2]. Additionally, these techniques can accurately recognize a location of user through learning only by collecting images from mobile camera. Among recent object pose estimation approaches available for VPS, methods which are counting on depth maps with color images have shown excellent performance [3,4,5]. However, depth-estimation cameras cannot measure depth outdoors or reflective objects; therefore, this approach is not always reliable. Additionally, depth-estimation cameras consume the battery of an additional mobile device according to the operation of the sensor. Among the indoor positioning methods, though a QRcode method with screenshot have a high accuracy, it also has a problem which the user’s position should be determined approximately.

The proposed system is a positioning system based on object pose estimation using images. Our method is used to estimate the position of user at specific indoor locations and provide 3D spatial information in 3D AR. Consequently, this can make user accurately estimate the position and pose of a camera in 3D space using a single-shot deep CNN based web application on a mobile device. After estimating the position of the camera in the 2D box of the object in 3D space. Pose estimation of the camera can stably determine the position through voxel indexing of the voxel database and provide 2D bird-eye view information. In addition, one of the eight vertices of the 3D box of the object is assigned as an anchor point of the 3D AR, and position information of the indoor space is provided to the user with 3D AR model.

The main contributions of this study are as follows.

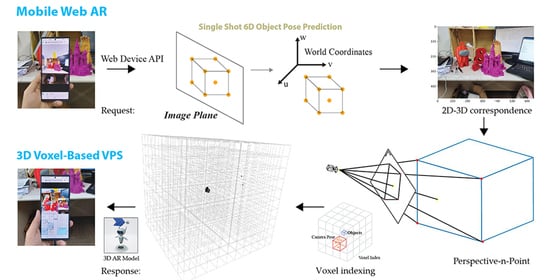
• We propose an indoor positioning system using a mobile web browser that users can easily access. The mobile client system uses a smartphone camera to acquire images and estimate the pose of the camera in the server system to ensure real-time indoor space.
• We improve a single-shot deep CNN based on 2D object recognition. The pose of the camera calculated using PnP is indexed to the voxel database. A visual positioning system is designed to determine the user location using a spatial voxel address.
• With the help of object pose estimation of single-shot Deep CNN, one object box in the camera pose is used as an anchor point for 3D AR to provide information on a 3D indoor space in 3D AR model.

Unlike previous studies that require user interface applications, our method does not require additional application installation. It is a low cast, fast, and sustainable VPS method with a mobile web browser and can provide users with a variety of location-based AR services.

The remainder of this paper is organized as follows. Section 2 reviews related work. The details of the system and method are described in Section 3. Experiments and evaluation are presented in Section 4, and the conclusions are presented in Section 5.

2. Related Research

2.1. 6D Object Pose Prediction

Recently, machine-learning-based 6D pose-prediction technologies have attracted more attention owing to the increased prevalence deep learning and neural networks. However, 6D pose estimation techniques based on deep learning encounter a unique problem. The accurate estimation of 6D poses of symmetrical objects using conventional deep learning methods is difficult. This is because the shape and the 6D pose of the object do not change on rotation when viewed from a fixed point. However, the corresponding ground truths differ. Zhang and Qi [6] generated the key point-wise features of the point clouds as input features and predicted the keypoint coordinates using a hierarchical neural network involving global point clouds with local information.

PoseCNN estimates the 6D poses of the translation and rotation of an object; 3D translation is performed by determining the center of the image and estimating its distance from the camera, and 3D rotation is performed by regressing to a quaternion representation [7]. This network consists of two stages: in the first stage, feature maps with different resolutions are extracted from the input image. These extracted data are shared across all the tasks performed by the network. In the second stage, the high-dimensional feature maps generated in the first stage are embedded into low-dimensional task-centric features. Subsequently, the network estimates 6D pose by performing the following three tasks: semantic labeling, 3D translation estimation, and 3D rotation regression. Augmented Autoencoder [8] enables the estimation 3D object orientation to facilitate the implicit representation of rotation using auto-encoders; the rotation vector that is most representative of the estimated rotation is obtained from a coded book and assigned to the corresponding estimated rotation.

The state-of-the-art method of 6D object pose estimation using RGB camera input is characterized by the following approaches: (1) detecting the 2D target of the object in the given image, and (2) matching the 2D–3D correspondence using the perspective-n-point (PnP) method for the 6D pose. This type of algorithm can be categorized into keypoint-based and dense 2D–3D correspondence approaches. The 6D pose of the camera using RGB-D image and 3D model and estimated by PnP algorithm is a structure-based localization method of visual positioning system [9].

Keypoint-based method: The pixel-wise voting network (PVNet) [10] regresses pixel-wise unit vectors to determine keypoints, uses these unit vectors to vote for keypoint locations using Random sample consensus (RANSAC) [11], and creates a flexible representation to localize keypoints. HybridPose [12] involves intermediate representation prediction networks and pose regression. The prediction networks take an image as an input and provides the corresponding predicted keypoints, edge vectors, and symmetry correspondences as output. The pose regression consists of two processes, namely initialization and refinement. Initialization solves a linear system problem to obtain an initial pose using the predicted intermediate estimations. HybridPose is robust against occlusion and truncation. BPnP [13] backpropagates the gradients through the PnP solver to update the weights and achieves learning using a solver from a geometric vision problem and an objective function. BB8 [14] is a comprehensive approach that applies a convolutional neural network (CNN) to the detected objects to predict their 3D poses based on 2D projections of the corners of their cuboid 3D bounding boxes. Single-shot deep CNN [15] predicts 2D projections of a cuboid by creating a 3D bounding box around objects using the CNN. The 6D pose is calculated using a PnP algorithm that employs these 2D coordinates and the 3D ground points for the bounding box corners.

DPOD [16] uses an additional refinement network that provides a truncated image of an object and an image patch that must be rendered separately using the predicted pose of the first step and provides the refined pose as output. CDPN [17] untangles the pose to predict rotation and translation separately. For detection, a fast-lightweight detector and fixed-size segmentation are used to determine the exact object region. For translation, estimation is conducted from the detected object region to avoid scale errors. Pix2Pose [18] predicts the 3D coordinates of individual pixels using the truncated area containing the object. In the pose estimation process, image and 2D detection results are inputs. While removing backgrounds and uncertain pixels, the predicted results are used to represent important pixels and adjust bounding boxes. Pixels with valid coordinates and small error predictions are obtained using the PnP algorithm with RANSAC.

2.2. 2D–3D Correspondence

Single-photo resection (SPR) is a basic element in photogrammetry and computer vision. SPR addresses the restoration of earth orientation parameters (EOPs) of a given image/object. The SPR problem is also known as space resection, the perspective 3-points (P3P) problem, or PnP for n-points.

Grunert (1841) introduced the first solution to P3P by applying the cosine law for light emitted from the perspective center to three image points and the corresponding object points from the perspective center. Lepetit et al. [19] reduced the problem to four virtual control points, which is expressed as a weighted sum for n (n ≥ 4) object points and developed an efficient PnP solution (EPnP). Li et al. [20] introduced a robust PnP (RPnP) solver that utilizes a subset of three points and produces an (n − 2) quaternary polynomial. The sum of squares of polynomials and the cost function are used to determine the minimum value via differentiation. A seventh-order polynomial of the differentiation of cost function is solved using the eigenvalue method [21].

The second SPR solution is an iterative method, which is the best approach to achieve high accuracy with minimal or redundant noisy data. However, these iterative methods are slow and approximate the position and orientation of parameter values.

The PnP problem and pose estimation from the projective observation of known points are related to the restoration of 6D poses given the central projection of n ≥ 3 known 3D points in the calibrated camera. It is extensively used in geometric computer vision systems and determines the camera pose (orientation/position and rotation/translation) from observations of n 3D points.

In the case of a minimum PnP with a finite number of solutions, three observations (n = 3) are required in a nondegenerate configuration. This is called the P3P problem. P3P solvers are either directed or triangulated. Direct methods parameterize the pose of the input coefficient using projection invariances. Therefore, feasibility constraints should be applied as a post-processing step on obtaining a solution. The triangulation method triangulates points under pose invariants in the camera coordinate system, considers the distance as an unknown and solves the pose. In this triangulation method, a user can determine the rotation by choosing either a quaternion or R ∈ SO (3). The geometric feasibility constraints, wherein each point is placed in front of the camera, limit the solutions before estimating the pose.

3. System and Methodology

This section outlines the proposed method and details the main modules and important algorithms involved. The proposed system consists of a mobile web and server. After the smartphone takes an image, it predicts a 6D object pose with an image which is transmitted to the server which estimates the pose of the camera, implements the remaining algorithms, and returns the result to. Figure 1 shows that the overall architecture of the proposed method includes three components: (a) acquiring images with a mobile web and single-shot deep CNN, (b) single-shot 6D object pose estimation, and (c) 3D voxel-based VPS.

3.1. System Overview

The proposed method is a mobile web implementation mechanism that outsources computing-intensive tasks to cloud servers, allowing web users to gain better location-based services and benefit from the server’s stronger computing capabilities. However, additional communication delays and deployment costs are two critical issues that should be simultaneously addressed. The 5G network may achieve a data rate of 1 Gb/s and an end-to-end delay of milliseconds.

Figure 1a shows pose estimation of a single-shot deep CNN 2D object, acquiring an image from a mobile web with a camera. A single-shot deep CNN algorithm uses the acquired image to estimate eight corner points and one central coordinate of the 2D object box in the image. (b) 2D to 3D conversion and camera position estimation: estimates the 3D box and pose of the object with the PnP algorithm of the computer vision with the 3D box and central coordination of the object estimated from the image and the mesh model of the 3D object and finally estimates the pose of the camera. (c) The pose and camera position of the camera are estimated through the displayed voxel index and the mobile web VPS: (a) and (b) processes may be different from ground truth. To reduce this error and estimate more accurate camera location (user location), the estimated location of camera is matched to a voxel index in the voxel database and transmitted to a mobile an updated voxel index.

3.2. 6D Object Pose Estimation

This section focuses on determining an accurate pose estimation method. The proposed method is designed to localize and estimate the orientation and translation of an object accurately without correction. An object pose is expressed as a rigid transformation (RT) from the object to the camera coordinate system, where R and t represent 3D rotation and transformation, respectively.

First, a 6D object pose estimation using RGB image data input is described to obtain rotation information.

If converting a point x₁ into x₂ in a three-dimensional space is represented via a matrix R, a mapping function from a point $X_1={\left[x_1{y}_1{z}_1\right]}^{\top }$ to $X_2={\left[x_2{y}_2{z}_2\right]}^{\top }$ is expressed as follows [22].

$$f : {\mathsf{ℝ}}^3 \to {\mathsf{ℝ}}^3 \left[ \begin{array}{c}\begin{array}{c}{x}_2\\ y_2\end{array}\\ z_2\end{array} \right]=R \left[ \begin{array}{c}\begin{array}{c}{x}_1\\ y_1\end{array}\\ z_1\end{array} \right]$$

(1)

In this case, the 3 × 3 matrix R set in which the inverse matrix exists corresponds to the general linear group GL (3, ℝ). Among these R, orthogonal matrices with a determinant of ± 1 are referred to as orthogonal groups. Therefore, there is a relationship between O (3) ⊂ GL (3, ℝ)). Among these transform matrices, the transformation in which the distance between two pairs of points does not change is called isometries; a matrix with a determinant of +1 is called property isometries. This special orthogonal group is referred to as SO (3). The SO (3) group which is under (SO (3) ⊂ O (3)) can only express pure rotation. Therefore, a 4 × 4 matrix is considered to express translation as shown in Equation (2); 3D points are extended to homogeneous coordinates. (GL (4, ℝ)).

The complete 6D pose is a three-dimensional orthogonal group, consisting of two parts: 3D rotation R ∈ SO (3) and 3D transformation t ∈ R³, as shown in Equation (3).

$$\left[\begin{array}{c}{X}_2\\ 1\end{array}\right]=T \left[\begin{array}{c}{X}_1\\ 1\end{array}\right]$$

(2)

$$\left[\begin{array}{c}\begin{array}{c}{x}_2\\ y_2\end{array}\\ \begin{array}{c}{z}_2\\ 1\end{array}\end{array}\right]=\left[ \begin{array}{c}\begin{array}{c}{R}_{11}\\ R_{21}\end{array}\\ \begin{array}{c}{R}_{31}\\ 0\end{array}\end{array} \begin{array}{c}\begin{array}{c} R_{12}\\ R_{22}\end{array}\\ \begin{array}{c}{R}_{32}\\ 0\end{array}\end{array} \begin{array}{c}\begin{array}{c}{R}_{13}\\ R_{23}\end{array}\\ \begin{array}{c}{R}_{33}\\ 0\end{array}\end{array} \begin{array}{c}\begin{array}{c}{t}_x\\ t_y\end{array}\\ \begin{array}{c}{t}_z\\ 1\end{array}\end{array} \right] \left[\begin{array}{c}\begin{array}{c}{x}_1\\ y_1\end{array}\\ \begin{array}{c}{z}_1\\ 1\end{array}\end{array}\right]$$

(3)

The 6D pose represents a rigid body transformation from object to camera coordinate system. This entire task has already been resolved in recent tasks in the field of relatively mature 2D object detection, as it includes several sub-tasks, such as detecting objects first in 2D images and processing multiple object categories and instances. In this study, we use the 2D object detection approach and improve it to predict the 6D pose of an object.

The proposed method is capable of end-to-end training that enables 6D pose prediction in real time and predicts the 2D projection of 3D bounding box corners surrounding objects. To regress the 2D boundary box as in the conventional YOLOv3 [23] and predict the projection of the 3D boundary box edge in the image, several additional 2D points are predicted for each object instance in the image. Considering these 2D coordinates and the 3D ground control point at the edge of the boundary box, 6D poses can be algebraically calculated using an efficient PnP algorithm [19].

The 6D pose estimation problem is formulated in terms of predicting the 2D image coordinates of the virtual 3D control point related to the 3D model of the object of interest. When considering 2D coordinate prediction, the 6D pose of the object is calculated using the PnP algorithm. The 3D model of each object is parameterized into nine control points. For these control points, eight corners of a tight 3D boundary box suitable for the 3D model are selected. Additionally, the center of the object’s 3D model is used as the ninth point. This parameter designation is common and can be used for all robust 3D objects with arbitrary shapes and topologies.

3.3. 2D–3D Correspondence—3D Position Estimation Utilizing Perspective-n-Point

The camera pose estimation method through 2D point response with n 3D data in computer vision is a fundamental problem. The most common approach to the problem is to estimate six degrees of freedom and five correction parameters (focus distance, pub, aspect ratio, and slope) of the pose. A well-known direct linear transformation (DLT) algorithm is used to set at least six correspondence relationships. However, there are several simplifications to the problem of changing to numerous algorithms that improve the accuracy of DLT. The most common simplification is to assume a known correction parameter, the so-called perspective-n-point problem.

Figure 2 shows that, when there are 3D points (in world coordinates) that match the 2D projection points (in image coordinates) for the object in the image acquired by the camera, the values of the camera’s orientation and position are estimated from the object. When a correspondence set between the 3D points $p_i$($X_i$, $Y_i$, $Z_i$) expressed in the reference frame of the spatial world coordinate system and the 2D projection $p{’}_i$($u_i$, $v_i$) for the image is given, the poses (R and T) for the camera are calculated.

$$s \left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[ \begin{array}{c}{f}_x\\ 0\\ 0\end{array} \begin{array}{c}\gamma \\ f_y\\ 0\end{array} \begin{array}{c}{c}_x\\ c_y\\ 1\end{array} \right] \left[ \begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array} \right] \left[ \begin{array}{c}x\\ y\\ z\\ 1\end{array} \right]$$

(4)

3.4. Voxel Index Database Using Camera Pose Optimization

The voxel database uses high-performance 3D sensors to scan indoor spaces. The sizes of the X, Y, and Z axes of the point cloud are calculated using the maximum and minimum values of the scanned point cloud coordinates. Voxel addresses are generated by dividing the calculated X, Y, and Z axes of the indoor space by the predefined voxel size and assigning a voxel address. The voxel address determines the location in the user’s space. The voxel database is reconstructed including the real location of the object (3D box central coordinates). The pose of the camera estimated from the image is converted into coordinates of the voxel database. The converted coordinates determine the location of the user using the voxel index.

3.5. Voxel Addressing vs. VPS Distance Error

The pose estimation of the estimated object is proportional to the center coordinates x, y, and z of the object and the rotational values of the object pitch, yaw, and roll, and the distance to the origin coordinates (0, 0, 0) of the camera. However, because VPS is made to the address of the voxel, the coordinates of the objects in the voxel database space are the same within the box of voxel labeling. Figure 3 shows that the VPS error rate is on average as much as the center distance of the voxel when the position of the camera and actual camera coordinates are not the same voxel in the voxel database space estimated by PnP of the improved single-shot deep CNN.

The actual camera position of the camera corresponding to the object center point of the voxel database of the object selected in the indoor space: ($x_2, y_2, z_2$) ∈ Voxel No.x2 and VPS predicted camera position through the pose of the camera estimated by the PnP algorithm: ($x_1, y_1, z_1$) ∈ Voxel No.x1. When points belong to the same voxel, the proposed method maps these points to same voxel index. This indexing reduces distance error of estimation of location. Assuming that length, width, and height have same size of α, the actual distance error in the same voxel space does not exceed Equation (5). Therefore, when the voxel number does not match, the distance error of the corresponding voxel is calculated by Equation (6).

$$(\mathrm{VPS} \mathrm{Distance} \mathrm{Error}=\mathrm{Max} \sqrt{3{\alpha }^2}) \in \{\mathrm{Voxel} \mathrm{No}.\mathrm{X}{2}_{ }=\mathrm{Voxel} \mathrm{No}.\mathrm{X}1\}$$

(5)

$$(\mathrm{VPS} \mathrm{Distance} \mathrm{Error}=\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2+{\left(z_2-z_1\right)}^2}) \in \{\mathrm{Voxel} \mathrm{No}.\mathrm{X}{2}_{ }\ne \mathrm{Voxel} \mathrm{No}.\mathrm{X}1\}$$

(6)

4. Evaluation

In this section, we compare the CNN of the 6D pose estimation base on RGB on LineMOD [24] with other 6D pose estimation methods for a single individual to measure the performance of the proposed system. It was designed on the premise of indoor use, and night, day, and lighting were not considered. Experiments focusing on real-time execution on the mobile web measured the network speed of cutting-edge methods. We compared three voxel sizes that can stabilize the camera’s pose with the proposed method’s voxel addressing. The VPS real-time criterion is at least 30 FPS; we describe the experiments we performed as experimental settings and error measurements with implementation details.

4.1. Experimental Setup

4.1.1. System Setup

The system facility conditions used in the experiment are as follows.

Mobile Web: A smartphone Galaxy Note 20 Ultra (SM-N986N) equipped with 108 million pixels and 12 GB RAM and tested in a Web (Chrome Browser) environment with 5G (fifth generation technology standard) mobile communication.

Server: The implementation was written in Python 3.6, using PyTorch for graphics processing unit (GPU) computation. The evaluation details measured the inference times on a desktop using a Linux Ubuntu 16.04 LTS, Ryzen 9 3900X CPU, and RTX 2080 SUPER 8G GPU.

4.1.2. LineMOD Dataset

The LineMod dataset is a popular and widely used benchmark dataset for 6D object pose estimation. It consists of 13 different entities arranged in 13 complex scenes. For each scene, only one object is annotated with a 6D pose; other objects can be viewed simultaneously. There is an example with approximately 1200 annotations per individual.

4.2. Comparison of 6D Pose Estimation Convolutional Neural Network Using RGB

We evaluated the runtime of the 6D pose estimation network for LineMOD datasets that have become the de facto standard benchmarks for 6D pose estimation. Among the latest methods of 6D pose estimation RGB in LineMOD that can be applied to our method, efficient pose [25], RePOSE [26], DPOD [16], HRNet (DSNT + BPnP) [13], HybridPose [12], CDPN [17], PoseCNN + DeepIM [27], E2E6DoF [28], PVNet [10], CullNet [29], SSD-6D [30], keypoint detector localization [31], single-shot deep CNN [15], BB8[14], Pix2Pose [18], and augmented autoencoder [32], which focused not only on accuracy but also on time cost were selected and evaluated. Because the proposed method and voxel index can optimize the user’s location accuracy by correcting the VPS error, the experimental evaluation selected the network based on real-time data on the mobile web rather than accuracy. Figure 4 depict the experimental results of the following three networks that were selected for evaluation on the LineMOD dataset considering the runtime: efficient pose, SSD-6D, and single-shot deep CNN. We used the trained model provided in each study. Figure 4 shows that, for each of the 13 classes provided by LineMOD, the efficient pose is φ = 0. The single trained tape model and SSD-6D used the provided trained bench vise model and trained hole puncher model weight provided by single-shot deep CNN to create boxes for supervised learning and boxes through 6D object pose estimation with 1000 evaluation datasets per class.

Table 1. Runtime performance comparison between single object pose estimation algorithms. LineMOD dataset is used.

6D Object Pose	Efficient Pose [25] (FPS)	SSD-6D [30] (FPS)	Single-Shot Deep CNN [15] (FPS)
Ape	20.56	11.98	54.36
Bench vise	20.50	11.32	53.99
Cam	20.69	11.45	54.30
Can	20.87	11.87	54.49
Cat	21.01	11.94	54.69
Driller	20.91	11.57	54.53
Duck	19.88	11.74	54.47
Eggbox	19.53	12.43	54.56
Glue	20.29	12.03	55.50
Hole puncher	19.84	11.83	54.16
Iron	21.67	11.78	53.96
Lamp	20.32	11.10	54.04
Phone	20.47	11.59	53.95
Average FPS	20.50	11.74	54.38

shows the average frame per second (FPS) evaluation table experimented with the learned weight provided by each network using 13 classes of 6D pose estimation networks in the widely used 6D pose estimation benchmark dataset LineMOD using RGB input. A total of 1000 evaluation images were used for each of the 13 classes. The 13 object classes are ape, bench vise, cam, can, cat, driller, duck, eggbox, glue, hole puncher, iron, and lamp. Although there is a slight difference between the runtime speed revealed in each paper and the system environment, similar runtime speeds could be identified overall, as revealed by the author of the network. The average FPS evaluated in the proposed system environment is as follows: Efficient pose 20.50 FPS, SSD-6D 11.74 FPS, and single-shot deep CNN 54.38 FPS were measured. To ensure the best real-time nature of the proposed method through these comparative evaluations, we selected a 3D pose estimation network for single-shot deep CNNs with a runtime rate higher than 50 FPS.

Figure 5 shows the overall process of the proposed method. When the mobile web client sends a request to the server with the image and receives the image from the server, it detects the object through the single-shot deep CNN network and converts the ratio of the coordinates of the 3D box on 2D into coordinate values suitable for the picture size. Using the PnP algorithm, converted 2D box coordinates, and the camera internal parameter of the detected object size, the camera pose coordinates relative to the object is obtained. VPS is performed by determining the relative coordinates as voxels in the voxel database. Figure 5 shows the process of responding to the user’s camera pose to the client of the mobile wed again and

Table 2. VPS speed measured by the proposed method system.

Request + Response	Detect	2D–3D Correspondence	Perspective-n-Point	Voxel Indexing	Total
700 ms	28.84 ms	0.069 ms	0.2178 ms	0.4 ms	733.1268 ms

summarizes the running time of each process for each step. The operating time of the entire system is 733.1268 ms, which can transmit VPS to the user’s mobile web once a second. The voxel indexing step includes the step of drawing the voxel on the server; however, it does not include the time required to send the image to the smartphone and the time taken to load the image.

4.3. VPS Results of Voxel Index

The pose estimation error of the improved single-shot deep CNN is proportional to the x, y, and z coordinates of the object center and the rotational pitch, yaw, and roll values of the object, and it is proportional to the origin coordinates (0, 0, 0) of the camera. However, because the VPS targets the address of the voxel, the coordinates of the camera in space remain unchanged within the indexed voxel box. Our method consists of a network module and an algorithm module, and it is computed using our equation in the algorithm, and the measurement uncertainty in our system is proportional to the estimations of network-specific. The measurement uncertainty estimated by the network is corrected using our method, by positioning through voxels. The improved single-shot deep CNN has an average error of VPS in the database space estimated by VPS when the position of the camera coordinates and the actual camera coordinates are not the same voxel. The actual camera position of an object selected in an indoor space, ($x_2, y_2, z_2$) ∈ Voxel No.X2 and VPS Predicated camera position through pose estimation of an extended single-shot deep ($x_1, y_1, z_1$) ∈ Voxel No.X1 are in the range of Equation (5). The actual distance error in the same voxel space does not exceed that obtained via Equation (5). However, when the voxel numbers do not match, the distance error is determined via Equation (6).

Table 3. Distance errors for the ground truth and estimated camera poses.

Voxel	Ape	Bench Vise	Cam	Can	Cat	Driller	Duck	Eggbox	Glue	Hole Puncher	Iron	Lamp	Phone	Average
Distance	10 cm	5 cm	7 cm	5 cm	8 cm	7 cm	9 cm	9 cm	8 cm	8 cm	11 cm	14 cm	11 cm	8.61 cm

shows the VPS distance error of the extended single-shot deep CNN pose estimation obtained using Equation (6). The voxel size of the voxel database is tested for the 20, 50, and 100 sizes, and the position may be localized within the accuracy of the sub meter level with respect to 80% or more at a voxel size of 50 cm. Table 3 shows that more than 95% of the 100 cm voxel size is successfully identified in the ground truth position.

Based on the object box center point of the indoor space, voxels of 2 m in width and height were divided into 1 m units along the x, y, and z axes, and addresses are formed in the divided voxel database space.

Table 4. Distance error comparison for voxel size (20 cm).

Voxel Index Error (20 cm)	Ape	Bench Vise	Cam	Can	Cat	Driller	Duck	Eggbox	Glue	Hole Puncher	Iron	Lamp	Phone	Average
1 Voxel (%)	34.8	27.3	35.5	27	36.5	32.9	36.4	36.3	31.8	35.8	37.9	33.6	38.4	34.2
2 Voxel (%)	10.2	4.7	6.9	4.1	10	8.6	10	10.8	8.4	7.6	13.5	9.9	13.4	9.1
3 Voxel (%)	2.2	0.6	1.0	0.1	1.3	1.1	1.2	1.1	1.1	0.8	2.5	1.0	1.8	1.2
4 Voxel + (%)	0.3	0.2	0.0	0.0	0.1	0.0	0.2	0.1	0.3	0.3	0.3	1.4	0.3	0.3

shows that 55.5% of the total voxels can be classified into the same voxel address when the voxel is divided into 20 cm.

Table 5. Distance error comparison for voxel size (50 cm).

Voxel Index Error (50 cm)	Ape	Bench Vise	Cam	Can	Cat	Driller	Duck	Eggbox	Glue	Hole Puncher	Iron	Lamp	Phone	Average
1 Voxel (%)	19.4	11.7	15.4	12.5	19.7	14.1	16.6	19	17.4	16.8	23.5	14.7	21	17.1
2 Voxel (%)	2.1	0.6	0.7	0.3	1.6	0.8	1	1.9	1	0.9	2.5	1.3	1.4	1.2
3 Voxel (%)	0.1	0.0	0.0	0.0	0.1	0.0	0.9	0.0	0.0	0.0	0.1	0.4	0.0	0.1
4 Voxel + (%)	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.6	0.1	0.1

shows that 81.7% is indexed to the same voxel address when divided by 50 cm, and

Table 6. Distance error comparison for voxel size (100 cm).

Voxel Index Error (100 cm)	Ape	Bench Vise	Cam	Can	Cat	Driller	Duck	Eggbox	Glue	Hole Puncher	Iron	Lamp	Phone	Average
1 Voxel (%)	4.6	3.7	4.7	3.9	6.0	4.5	5.0	4.5	4.0	5.6	5.6	4.8	5.2	4.8
2 Voxel (%)	0.0	0.0	0.1	0.0	0.0	0.0	0.2	0.0	0.1	0.1	0.0	0.4	0.0	0.1
3 Voxel (%)	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
4 Voxel + (%)	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0

shows that 95.2% is indexed within the same voxel address when divided by 1 m.

As shown in

Table 7. Distance error comparison of 6D pose estimation via the EfficientPose network according to VPS Voxel Size.

Voxel Index Error (50 cm)	Ape	Bench Vise	Cam	Can	Cat	Driller	Duck	Eggbox	Glue	Hole Puncher	Iron	Lamp	Phone	Average
1 Voxel (%)	13.3	13.2	10.0	14.0	12.8	11.3	12.3	3.2	7.7	11.5	9.4	10.8	10.8	10.8
2 Voxel (%)	0.6	0.6	0.7	0.9	1.0	0.4	1.2	15.3	12.4	0.3	0.4	0.3	0.4	2.7
3 Voxel (%)	0.0	0.1	0.1	0.3	0.1	0.0	0.1	5.8	4.6	0.0	0.0	0.0	0.0	0.9
4 Voxel + (%)	0.1	0.0	0.0	0.1	0.1	0.0	0.0	61.7	34.3	0.0	0.0	0.0	0.0	7.4

, the 6D pose estimation accuracy excluding the eggbox and glue classes of EfficientPose in our experiment is 5.68% higher than the estimated accuracy of Single-shot Deep CNN; however, the time rate achieved by EfficientPose is 20.50 FPS, as shown in Table 7, and the error rate is higher in a specific class. Figure 6 shows an example of the LineMOD dataset. Figure 6a displays the input RGB image and the ground truth pose in red with the estimated pose of the extended single-shot Deep CNN in blue, and Figure 6b displays of a voxel database with a voxel labeling index.

5. Conclusions

In this study, we introduced a system that determines a user’s location using a highly scalable, end-to-end 6D object posture estimation approach based on the state-of-the-art 2D object detection architecture of the single-shot deep CNN. We improved the architecture in an intuitive and efficient manner to perform 6D object pose estimation of multiple objects and instances and 2D object detection while maintaining the advantages of the underlying network and keeping additional computational costs low. Based on the object, a positioning system in a large indoor space using a smartphone camera was proposed. The system used a web on smartphones to detect specific objects indoors and calculated a user’s location. The system integrated deep learning and computer vision algorithms and proposed the VPS that could determine the position of an object and pose estimated through deep learning by matching the position and pose of the object in space with a predefined. It is a visual positioning system that used a voxel address that can determine a user’s location by learning images acquired by a camera on the mobile web through deep learning, estimating the pose of an object, and matching the camera pose in a predefined voxel indexing space. The proposed method organized a database with voxel addresses to determine a location of user. This shows that the proposed method can efficiently lead to high location accuracy and direction estimation in a well-known space. The proposed system uses web-based images of mobile devices that users can easily access when GPS is insufficient, and is a deep learning-based visual positioning which uses fixed specific location to provide 3D AR contents to users. The proposed method is particularly suitable for scenarios that ensure real-time performance.