1. Introduction
Three-phase pulse-width modulating (PWM) rectifiers have been widely used in the fields of electric vehicles, aerospace, renewable energy, high power electrolysis, and military [
1]. Compared with the conventional diode or thyristor rectifiers, PWM rectifiers have many merits, e.g., lower harmonic distortion of line current, stabilization, and regulation of the DC-link monitoring signal [
2]. However, due to complex operating conditions and unpredictable work performance, the PWM rectifiers are vulnerable to unexpected faults. Once fault occurs, the system runs under abnormal conditions or causes substantial economic losses. Hence, an efficient and accurate fault diagnosis approach is of the utmost to ensure the reliability and security of the PWM rectifiers [
3].
In general, the semiconductor switch device faults in power converters are divided into two categories: hard fault (structural fault) and soft fault (parametric fault) [
4,
5,
6]. Hard faults cause the circuit topology to change due to component damage, resulting in a complete loss of circuit function. The soft fault manifests that the parameter value of the component exceeds the tolerance range of the nominal value. Additionally, the hard faults of the power semiconductor devices are the most common in PWM rectifiers, which can be divided into short-circuit fault (SCF) and open-circuit fault (OCF) [
7]. A SCF of the semiconductor switch device will cause an overcurrent, which is very destructive and makes the PWM rectifier shut down immediately. In practice, hardware protection circuits are adopted while a SCF is detected, a fast-acting fuse disconnects for converting a SCF to an OCF [
8]. In contrast, an OCF will not immediately cause the shutdown of the system and can remain undetected for an extended period. This may cause overstress on the healthy switches, leading to the second fault of other components [
9].
Nowadays, fault diagnosis approaches are classified into model-based approaches [
10] and data-driven approaches [
11]. Model-based approaches are dependent on the empirical knowledge of the operation conditions, material characteristics, and failure mechanism to build mathematical models, among which the state estimation method, parameter identification method [
12], and analytical model method [
13] are representative. However, the two-level three-phase PWM rectifier has a symmetrical topology structure with many power semiconductor devices. The mixed-signal, formed by noise and crosstalk of neighboring power semiconductor device, makes the original monitoring signal relatively easy to be distorted, resulting in a low signal-to-noise ratio [
14]. Thus, the model-based method can hardly build a precise fault diagnosis model for a two-level, three-phase PWM rectifier. In this case, the data-driven approaches emerge with the advantage that prior expertise on accurate mathematical models is no longer required. Data-driven approaches mainly involve three parts: feature extraction, feature selection, and fault diagnosis.
Currently, numerous feature extraction researches have been widely utilized to capture fault information from the original monitoring signal via time-domain and frequency-domain feature extraction. For time-domain statistical analysis, reference [
15] employed kurtosis and entropy of the original monitoring signal as the fault features of the circuit. Long et al. extracted the high-order statistical parameters as features for the diagnosis of the circuit [
16]. Nevertheless, these time-domain methods are unable to provide information in specific frequency bands, which makes it challenging to extract useful fault information. For frequency-domain feature extraction, the fast Fourier transform (FFT) is used for spectrum analysis, and the wavelet transform is used for sweep frequency response analysis of the output signal [
17]. However, these approaches show poor distinguishability for insufficient fault features for nonlinear and non-stationary signals. Another powerful signal processing method for non-linear and non-stationary signals, named empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD) [
18], and complete ensemble empirical mode decomposition (CEEMD) [
19], has been widely used to solve fault diagnosis of rotating machinery and circuit systems. Additionally, compared with wavelet transform where the basic functions are fixed, the EMD-based method decomposes signals according to time-scale characteristics of data without setting any basis function in advance, which has stronger local stationary. However, the EEMD and CEEMD algorithms are time-consuming, the number of iterations has a great impact on the decomposition effect. Therefore, this paper uses a modified ensemble empirical mode decomposition (MEEMD) [
20,
21] algorithm to extract fault features of the three-phase PWM rectifier, which not only suppress the mode confusion in the decomposition process, but also reduce the calculation amount.
Feature selection, the most significant step before fault diagnosis, can exclude redundant features and remain representative features [
22]. If all the features are imported into the classifier directly without further processing, it will increase the computational complexity. However, there is a common problem concerning what features would make fault diagnosis more accurate. To answer this question, the existing approaches generally applied suitable projections to map the matrices in a feature subspace capturing high-discriminative fault information. A variety of approaches, i.e., independent component analysis (ICA), kernel principal component analysis (KPCA), two-dimensional non-negative matrix factorization (2DNMF), and two directions two-dimensional linear discriminative analysis (TD2DLDA), are implemented to increase the discrimination between different fault categories via further obtaining the lower-dimension feature vectors. Although the above methods allow the user to pick better features and achieve good results for circuit fault diagnosis, there are still drawbacks. For instance, a suitable feature is always difficult to select when the data volume is not large because of insufficient information. In other words, the features selected in this way are likely not comprehensive, and some useful information may be overlooked. Thus, in this work, the Extremely randomized trees (ERT) algorithm is used to measure the importance of each feature. The best subset of features can be selected via dimensionality reduction.
Nowadays, there are many shallow learning fault diagnosis models, i.e., backpropagation neural network (BPNN), support vector machine (SVM) [
23], least squares support vector machine (LSSVM), multiclass relevance vector machine (mRVM) [
24], and extreme learning machine (ELM) [
25], which have been widely implemented in fault diagnosis. For example, artificial neural network (ANN) is used to implement intelligent classification, in which the dependency and the number of thresholds can be reduced [
26]. In [
27], an intelligent fault diagnosis method based on an immune neural network is used to acquire fault knowledge of electronic components. Nevertheless, these shallow learning networks can not reveal the complex inherent relationships between the root cause of failure and the signal signatures, which often suffer from invalid learning and weak generalization when learning and training with many fault features. Moreover, various optimization algorithms, such as the genetic algorithm (GA), quantum-behaved, chaos theory, particle swarm optimization (PSO) [
16], and crow search algorithm (CAS) [
28], have been applied to optimize the hyper-parameters of the above shallow learning models. Hereafter, deep learning models have been emerged as a practical approach due to its powerful generalization ability by learning the mapping relationship between the available fault feature and the corresponding fault category. Currently, several effective deep learning models have been applied in fault diagnosis, i.e., deep belief network (DBN) [
29], sparse auto-encoder (SAE). For instance, Sun et al. [
28] presented a novel DBN model optimized by the CAS to realize fault diagnosis for a DC-DC circuit. In [
30], Wen et al. investigated a new deep transfer learning method for fault classification, which is a supervised transfer learning based on a three-layer SAE. In [
31], the proponent of the DBN algorithm said that DBN could overcome the limitation of shallow neural networks. DBN is composed of multi-layer units, which can learn to obtain a feature vector that is more suitable for classification. However, the performance of DBN is very vulnerable to the change of DBN structure, such as the depth of the model and the number of hidden layer units. In [
32], extensive experiments had been carried out by Coates et al., and the results showed that the number of hidden layer units had a more critical effect on the performance of DBN than the depth. It is necessary to propose a suitable optimization algorithm to determine the number of hidden layer units of DBN.
Consequently, this paper proposes a novel fault diagnostic approach for a two-level three-phase PWM rectifier based on beetle antennae search optimized deep belief network (BAS-DBN). The main contributions of this paper are summarized as follows:
(1) As an improved EMD-based algorithm, MEEMD overcomes the shortcomings of EEMD and CEEMD. It has less computation time and higher reconstruction accuracy when decomposing the original signal into more representative intrinsic mode function (IMF) components. For fully mining sensitive features, the ERT algorithm is proposed to analyze features from multiple respects to obtain the optimal feature set. Feature selection can avoid feature redundancy and overfitting, thereby improving the accuracy of the fault classifier and constructing a faster and lower-consumption fault diagnosis model.
(2) The DBN can find out the essential structure of the data through the layer-by-layer nonlinear mapping and finally realize the deep extraction of features. The BAS algorithm is used to optimize the number of hidden nodes in DBN, avoiding critical deficiencies such as the premature convergence to sub-optimal solutions. Simulation results show that the proposed method achieves higher accuracy by comparing it with the other shallow learning models and optimization algorithms.
The rest of this paper is organized as follows.
Section 2 presents the methodologies and theoretical of feature extraction, feature selection, and fault diagnosis algorithms. In
Section 3, the simulation model of a two-level three-phase PWM rectifier is presented, and the fault categories are analyzed.
Section 4 presents the experimental results of different classification methods compared with BAS-DBN. The conclusion and future researches are presented in
Section 5.
2. Proposed Framework & Theoretical
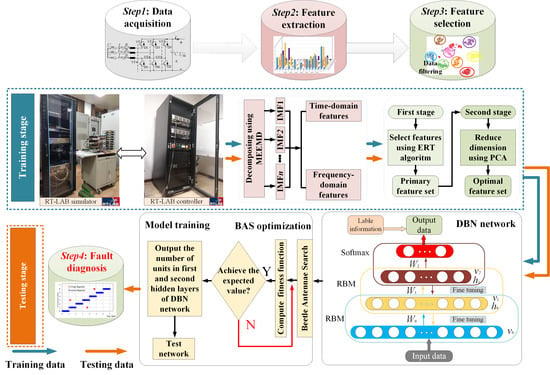
The proposed fault diagnostic strategy for a two-level three-phase PWM rectifier is represented in
Figure 1, and the detailed description is illustrated as follows:
Step 1: The healthy condition and fault modes for a two-level three-phase PWM rectifier are defined. The fault monitoring signal and the reference signal under the healthy condition and different OCFs are sampled from the two-level three-phase PWM rectifier.
Step 2: The initial feature vectors are extracted from the monitored current signals based on MEEMD. In detail, time-domain, frequency-domain, and energy characteristics of each IMF component are computed as the circuit fault features.
Step 3: The ERT algorithm calculates the importance of each fault feature, and the threshold value is set to remove the features with redundancy and interference. Afterward, the principal component analysis (PCA) algorithm is used to reduce the dimension of fault feature vectors for decreasing the calculation costs and improving the efficiency of fault diagnosis.
Step 4: The optimized DBN-BAS algorithm is utilized to achieve an intelligent fault diagnosis of the two-level three-phase PWM rectifier by optimizing and determining the optimal number of the neurons in the first and second hidden layers of DBN.
2.1. Modified Ensemble Empirical Mode Decomposition
The essence of the MEEMD algorithm [
33] is to use a certain rule to separate the abnormal signals in the original data, and then perform EMD decomposition on the remaining signals. Such processing can not only ensure the completeness of the original data, but also reduce the influence of abnormal signals on the decomposition results. The MEEMD algorithm avoids these problems by introducing the permutation entropy (PE) to randomly detect the abnormal signals. The steps of MEEMD are as follows:
Step 1: Add the positive and negative paired white noise
and
into the original signal
x(
t) to obtain a new sequence:
where
is the amplitude of the white noise signal.
represents the white noise, of which the root mean square value should be close to the root mean square value of
x(
t).
denotes the logarithm of the white noise, generally not higher than 100. Perform an EMD algorithm on
and
to obtain the IMF component series
and
, from which the first IMF component
can be obtained via ensemble averaging.
Step 2: Based on the permutation entropy of the obtained IMF component, if the permutation entropy of the IMF component is greater than the threshold, it is an abnormal component. Otherwise, it is a stationary component. If is an abnormal component, continue to step 1 until the obtained IMF component is no longer abnormal.
Step 3: The abnormal components are separated from the original signal, and then the remaining is decomposed by the EMD algorithm. Finally, arrange all the IMF components obtained from high frequency to low frequency.
where
represents the sum of all abnormal signals,
denotes the residual signals, and
is the
kth IMF components obtained via the MEEMD algorithm.
2.2. Extremely Randomized Trees
The ERT algorithm [
34], which is proposed by Pierre Geurts et al., calculates the variable importance measures (VIM) of feature by calculating the purity of decision tree nodes by the Gini index. At last, a certain proportion of features are deleted according to the VIM value to obtain an optimal feature set.
Assuming that there are
m features
, the VIM value of each feature is expressed as
, representing the average change in the impurity purity of the
jth feature in the ERT decision trees. The formula for calculating the Gini index is as follows:
where
K represents the number of categories with samples.
represents the proportion of category
k in node m, and
.
For the importance of feature
at node
m, the variation of the Gini index before and after the branch of node
m is expressed as follows:
where
and
represent the Gini index of the two new nodes after branching, respectively.
If the node of the feature in the decision tree
i is in the set
M, then the importance of
in the
ith tree is expressed as follows:
Ultimately, the importance score of the feature is obtained by normalization as follows:
2.3. Deep Belief Network
The concept of DBN put forward by Hinton et al. in 2006 was an area of machine learning research, which overcame the limitations of shallow network methods. It is constructed from multiple layers of restricted Boltzmann machines (RBMs), which can extract deep-seated features from complex data. DBN can be viewed as the stacking of simple learning modules. DBN training consists of unsupervised layer-by-layer pre-training and supervised fine-tuning. The former achieves complex nonlinear mapping by directly mapping data from input to output, which is also the critical factor for its robust feature extraction capability. After pre-training, the DBN is trained, supervised by adding a classifier at the top level of DBN to reduce training error. This classifier uses a backpropagation algorithm to fine-tune the relevant parameters of the DBN.
As shown in
Figure 2, the schematic representation contains three stacked RBMs. The input layer is the visible layer, which is composed of n visible units
. Hidden1 is the first hidden layer, which is composed of
m hidden units
. Both are binary random vectors, i.e.,
,
. Since RBM is an energy-based model, the energy function
is defined as follows:
where
,
and
represent the bias of
and
;
is the weight that connects
and
. Then, the probability distribution to every possible pair of
v and
h can be defined as the following energy function
where
Z is the normalizing constant, as expressed in Formula (11). It can be calculated by summing all possible pairs of
and
The probability that the network assigns to
is as follows:
Furthermore, there is a bidirectional connection between the hidden layer and visible layer, while the neurons in the same layer are independent of each other. When the visible layer is determined, the conditional probability of the visible layer units is presented as follows:
The function
can be used to calculate the following activation probabilities
Given the training data, the probability
of Formula (12) can be maximized by adjusting corresponding parameters. The probability of a training vector is related to the energy of the vector. Therefore, the parameters of RBM can be estimated based on the principle of maximum likelihood estimation. The log-likelihood derivative of
can be derived as follows:
where
and
denote the expectation of
concerning the data distribution and the model, respectively. However, it is quite challenging to attain an unbiased sample of
. The learning rule is similar to the objective gradient function named contrastive divergence, where
can be replaced by
k iterations of Gibbs sampling. Therefore, according to Formula (15), the update rules of the model parameters are as follows:
where
is the learning rate.
2.4. DBN Optimized by Beetle Antennae Search Algorithm
In this paper, a DBN with two hidden layers is selected for fault diagnosis of a two-level three-phase PWM rectifier. The BAS optimization algorithm is used to the optimal number of neurons in the hidden layer of the DBN. Similar to the GA and PSO optimization algorithms, BAS can automatically implement the optimization process without knowing the specific form of function and gradient information. Furthermore, there is only one individual, and the speed of optimization has been significantly improved. The dimension of the search space in BAS is 2.
The biological principle of the BAS algorithm can be interpreted that the two antennae of the beetle judge the strength of the food odor on the left and right sides to determine the direction in the next step. The flow chart of the BAS algorithm can be summarized in
Figure 3, which can be divided into the following steps:
(1) Suppose there is a k-dimensional optimization space,
and
represent the coordinates of the left and right antennae of the beetle, respectively.
represent the centroid position of the beetle at time
t, and
represent the distance between the two antennae. If the initial orientation of the beetle is random, the vector that the left antennae of the beetle point to the right antennae is also arbitrary. Hence, a normalized random vector is assumed as follow
where
and
can be expressed as the centroid position
(2) The objective function is set as and the objective function value at the two position coordinates of the left and right antennae are calculated as and . Compare the size of these two values and choose the right or left step of the beetle position according to the optimization direction of the objective function .
(3) Subsequently, the beetle’s centroid position at time
t + 1 is updated as follows:
The fitness function is set as follow
where
denotes the output value of the DBN classifier and
denotes the actual value.
3. Results Establishment of the Simulation Model and Analysis of Fault Categories
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation as well as the experimental conclusions that can be drawn. The simulation experiment is carried out for the two-level three-phase PWM rectifier, which converts 220 V AC voltage to 600 V DC voltage with a switching frequency of 10 kHz.
Figure 4 shows the two-level three-phase PWM rectifier, which involves the main circuit and a control block diagram. The control block includes two current control loops and one DC-link voltage control loop. Furthermore, the AC-link current is converted to
d and
q axis current in a synchronous reference frame. The
q-axis current is kept at zero to achieve unity power factor operating status. Additionally, the
d-axis current is controlled to keep the DC-link voltage constant. The specifications of the circuit are listed in
Table 1.
Since the multiple power semiconductor devices are unlikely to break down simultaneously, this paper only considers the fault of one power semiconductor device. According to the topology of the circuit, the circuit fault categories are divided into seven categories, including healthy condition and VT
1-VT
6 OCFs.
Table 2 lists the fault modes, classification labels, and fault codes. More precisely, the classification label [0,1,0,0,0,0,0,0,0]T indicates that an OCF occurs at VT
1. In this paper, the MATLAB/Simulink model of the tested three-phase PWM rectifier is applied to the RT-LAB hardware-in-the-loop simulation system by PC, which reduces the difficulty of constructing the circuit and improves the reliability of the simulation system. Additionally, the data processing methods mentioned are implemented with MATLAB R2019a. As illustrated by
Figure 5, the simulation experimental of the two-level three-phase PWM rectifier was built in the OP5600 simulator, which constructs a circuit response database containing multiple fault conditions and transmits the fault signal to the PC. The circuit response was captured at the output using a National Instruments (NI) USB-6212 data acquisition board. The data were recorded using LabVIEW on PC. The experiment operations and different fault settings are implemented in the OP5607 controller.