Genome-Scale Metabolic Modeling with Protein Expressions of Normal and Cancerous Colorectal Tissues for Oncogene Inference
Abstract
:1. Introduction
2. Materials and Methods
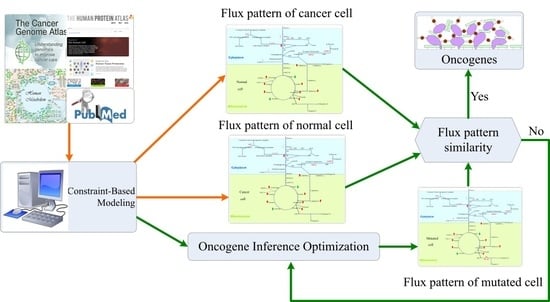
2.1. Reconstruction of GSMNs
2.2. Flux Balance Analysis
2.3. Oncogene Inference Problem
2.4. Association of Gene-Protein-Reaction
2.5. Nested Hybrid Differential Evolution Algorithm
3. Results and Discussion
3.1. Templates of Flux Patterns for Cancer and Normal Cells
3.2. Inferred Oncogenes
3.3. Performance of Enzyme Pseudo-Coding
3.4. Flux Variability Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AKT1 | AKT Serine/Threonine Kinase 1 |
| AGXT | Alanine–Glyoxylate And Serine–Pyruvate Aminotransferase |
| BL | Basal |
| CA | Cancer |
| CAT | Catalase |
| CDK8 | Cyclin Dependent Kinase 8 |
| CDO1 | Cysteine Dioxygenase Type 1 |
| CRC | Colorectal Cancer |
| CYBRD1 | Cytochrome B Reductase 1 |
| EGFR | Epidermal Growth Factor Receptor |
| FAP | Familial Adenomatous Polyposis |
| FBA | Flux Balance Analysis |
| FVA | Flux Variability Analysis |
| G6PC3 | Glucose-6-Phosphatase Catalytic Subunit 3 |
| G6PD | Glucose-6-Phosphate Dehydrogenase |
| GLRX2 | Glutaredoxin 2 |
| GPI | Glucose-6-Phosphate Isomerase |
| GRHPR | Glyoxylate And Hydroxypyruvate Reductase |
| GSMM | Genome-Scale Metabolic Model |
| H6PD | Hexose-6-Phosphate Dehydrogenase/Glucose 1-Dehydrogenase |
| HMGCL | 3-Hydroxy-3-Methylglutaryl-CoA Lyase |
| HNPCC | Hereditary Nonpolyposis Colon Cancer |
| HT | Healthy |
| IMPDH1 | Inosine Monophosphate Dehydrogenase 1 |
| LFCm | Logarithmic Fold Change Ratio |
| LIPC | Lipase C, Hepatic Type |
| MAPK1 | Mitogen-Activated Protein Kinase 1 |
| MLYCD | Malonyl-CoA Decarboxylase |
| mTOR | Mammalian Target Of Rapamycin |
| MYC | Myc Proto-Oncogene Protein |
| PPA2 | Pyrophosphatase (Inorganic) 2 |
| PPI | Protein-Protein Interaction |
| PRODH2 | Proline Dehydrogenase 2 |
| PYCR3 | Pyrroline-5-Carboxylate Reductase 3 |
| SLC26A6 | Solute Carrier Family 26 Member 6 |
| SLC37A4 | Solute Carrier Family 37 Member 4 |
| SLC9A1 | Solute Carrier Family 9 Member A1 |
| TLOP | Triple-Level Optimization Problem |
| TP53 | Tumor Protein P53 |
| UFD | Uniform Flux Distribution |
References
- Morozova, O.; Marra, M.A. Applications of next-generation sequencing technologies in functional genomics. Genomics 2008, 92, 255–264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barrett, T.; Wilhite, S.E.; Ledoux, P.; Evangelista, C.; Kim, I.F.; Tomashevsky, M.; Marshall, K.A.; Phillippy, K.H.; Sherman, P.M.; Holko, M.; et al. NCBI GEO: Archive for functional genomics data sets–update. Nucleic Acids Res. 2013, 41, D991–D995. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uhlen, M.; Oksvold, P.; Fagerberg, L.; Lundberg, E.; Jonasson, K.; Forsberg, M.; Zwahlen, M.; Kampf, C.; Wester, K.; Hober, S.; et al. Towards a knowledge-based Human Protein Atlas. Nat. Biotechnol. 2010, 28, 1248. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S.; Feunang, Y.D.; Marcu, A.; Guo, A.C.; Liang, K.; Vázquez-Fresno, R.; Sajed, T.; Johnson, D.; Li, C.; Karu, N.; et al. HMDB 4.0: The human metabolome database for 2018. Nucleic Acids Res. 2018, 46, D608–D617. [Google Scholar] [CrossRef] [PubMed]
- Winter, G.; Krömer, J.O. Fluxomics – connecting ‘omics analysis and phenotypes. Environ. Microbiol. 2013, 15, 1901–1916. [Google Scholar] [CrossRef] [PubMed]
- Asgari, Y.; Zabihinpour, Z.; Salehzadeh-Yazdi, A.; Schreiber, F.; Masoudi-Nejad, A. Alterations in cancer cell metabolism: The Warburg effect and metabolic adaptation. Genomics 2015, 105, 275–281. [Google Scholar] [CrossRef]
- Jalili, M.; Gebhardt, T.; Wolkenhauer, O.; Salehzadeh-Yazdi, A. Unveiling network-based functional features through integration of gene expression into protein networks. Biochim. Biophys. Acta (BBA) Mol. Basis Dis. 2018, 1864, 2349–2359. [Google Scholar] [CrossRef]
- Bordbar, A.; Monk, J.M.; King, Z.A.; Palsson, B.O. Constraint-based models predict metabolic and associated cellular functions. Nat. Rev. Genet. 2014, 15, 107. [Google Scholar] [CrossRef]
- Duarte, N.C.; Becker, S.A.; Jamshidi, N.; Thiele, I.; Mo, M.L.; Vo, T.D.; Srivas, R.; Palsson, B.Ø. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc. Natl. Acad. Sci. USA 2007, 104, 1777–1782. [Google Scholar] [CrossRef] [Green Version]
- Thiele, I.; Swainston, N.; Fleming, R.M.T.; Hoppe, A.; Sahoo, S.; Aurich, M.K.; Haraldsdottir, H.; Mo, M.L.; Rolfsson, O.; Stobbe, M.D.; et al. A community-driven global reconstruction of human metabolism. Nat. Biotechnol. 2013, 31, 419. [Google Scholar] [CrossRef]
- Ma, H.; Sorokin, A.; Mazein, A.; Selkov, A.; Selkov, E.; Demin, O.; Goryanin, I. The Edinburgh human metabolic network reconstruction and its functional analysis. Mol. Syst. Biol. 2007, 3, 135. [Google Scholar] [CrossRef] [PubMed]
- Mardinoglu, A.; Agren, R.; Kampf, C.; Asplund, A.; Nookaew, I.; Jacobson, P.; Walley, A.J.; Froguel, P.; Carlsson, L.M.; Uhlen, M.; et al. Integration of clinical data with a genome-scale metabolic model of the human adipocyte. Mol. Syst. Biol. 2013, 9, 649. [Google Scholar] [CrossRef] [PubMed]
- Brunk, E.; Sahoo, S.; Zielinski, D.C.; Altunkaya, A.; Dräger, A.; Mih, N.; Gatto, F.; Nilsson, A.; Preciat Gonzalez, G.A.; Aurich, M.K.; et al. Recon3D enables a three-dimensional view of gene variation in human metabolism. Nat. Biotechnol. 2018, 36, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Swainston, N.; Smallbone, K.; Hefzi, H.; Dobson, P.D.; Brewer, J.; Hanscho, M.; Zielinski, D.C.; Ang, K.S.; Gardiner, N.J.; Gutierrez, J.M.; et al. Recon 2.2: From reconstruction to model of human metabolism. Metabolomics 2016, 12, 109. [Google Scholar] [CrossRef]
- Agren, R.; Bordel, S.; Mardinoglu, A.; Pornputtapong, N.; Nookaew, I.; Nielsen, J. Reconstruction of genome-scale active metabolic networks for 69 human cell types and 16 cancer types using INIT. PLoS Comput. Biol. 2012, 8, 1–9. [Google Scholar] [CrossRef]
- Folger, O.; Jerby, L.; Frezza, C.; Gottlieb, E.; Ruppin, E.; Shlomi, T. Predicting selective drug targets in cancer through metabolic networks. Mol. Syst. Biol. 2011, 7, 501. [Google Scholar] [CrossRef]
- Jerby, L.; Shlomi, T.; Ruppin, E. Computational reconstruction of tissue-specific metabolic models: application to human liver metabolism. Mol. Syst. Biol. 2010, 6, 401. [Google Scholar] [CrossRef]
- Machado, D.; Herrgård, M. Systematic evaluation of methods for integration of transcriptomic data into constraint-based models of metabolism. PLoS Comput. Biol. 2014, 10, e1003580. [Google Scholar] [CrossRef] [Green Version]
- Opdam, S.; Richelle, A.; Kellman, B.; Li, S.; Zielinski, D.C.; Lewis, N.E. A systematic evaluation of methods for tailoring genome-scale metabolic models. Cell Syst. 2017, 4, 318–329. [Google Scholar] [CrossRef] [Green Version]
- Vlassis, N.; Pacheco, M.P.; Sauter, T. Fast reconstruction of compact context-Specific metabolic network models. PLoS Comput. Biol. 2014, 10, e1003424. [Google Scholar] [CrossRef]
- Wang, Y.; Eddy, J.A.; Price, N.D. Reconstruction of genome-scale metabolic models for 126 human tissues using mCADRE. BMC Syst. Biol. 2012, 6, 153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, M.; Chan, C. Human metabolic network: Reconstruction, simulation, and applications in systems biology. Metabolites 2012, 2, 242–253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schultz, A.; Qutub, A.A. Reconstruction of tissue-specific metabolic networks using CORDA. PLoS Comput. Biol. 2016, 12, 1–33. [Google Scholar] [CrossRef] [PubMed]
- The Cancer Genome Atlas Program. National Cancer Institute of U.S. Department of Health and Human Services. 2019. Available online: https://www.cancer.gov/tcga (accessed on 1 November 2019).
- Yizhak, K.; Chaneton, B.; Gottlieb, E.; Ruppin, E. Modeling cancer metabolism on a genome scale. Mol. Syst. Biol. 2015, 11, 817. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2018. CA Cancer J. Clin. 2019, 68, 7–30. [Google Scholar] [CrossRef]
- Taiwan Health Promotion Administration. Taiwan Cancer Registry, Cancer Statistics: Incidence and Mortality Rates for the Top 10 Cancer in Taiwan, 2008–2014. 2018. Available online: http://tcr.cph.ntu.edu.tw/main.php?Page=N2 (accessed on 24 November 2018).
- Nam, H.; Campodonico, M.; Bordbar, A.; Hyduke, D.R.; Kim, S.; Zielinski, D.C.; Palsson, B.O. A systems approach to predict oncometabolites via context-specific genome-scale metabolic networks. PLoS Comput. Biol. 2014, 10, e1003837. [Google Scholar] [CrossRef] [Green Version]
- Burgard, A.P.; Pharkya, P.; Maranas, C.D. Optknock: A bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol. Bioeng. 2003, 84, 647–657. [Google Scholar] [CrossRef]
- Pharkya, P.; Burgard, A.P.; Maranas, C.D. OptStrain: A computational framework for redesign of microbial production systems. Genome Res. 2004, 14, 2367–2376. [Google Scholar] [CrossRef] [Green Version]
- Pharkya, P.; Maranas, C.D. An optimization framework for identifying reaction activation/inhibition or elimination candidates for overproduction in microbial systems. Metab. Eng. 2006, 8, 1–13. [Google Scholar] [CrossRef]
- Ranganathan, S.; Suthers, P.F.; Maranas, C.D. OptForce: An optimization procedure for identifying all genetic manipulations leading to targeted overproductions. PLoS Comput. Biol. 2010, 6, e1000744. [Google Scholar] [CrossRef]
- Wang, F.S.; Wu, W.H. Optimal design of growth-coupled production strains using nested hybrid differential evolution. J. Taiwan Inst. Chem. Eng. 2015, 54, 57–63. [Google Scholar] [CrossRef]
- Kim, J.; Reed, J. OptORF: Optimal metabolic and regulatory perturbations for metabolic engineering of microbial strains. BMC Syst. Biol. 2010, 4, 53. [Google Scholar] [CrossRef] [Green Version]
- Pozo, C.; Miró, A.; Guillén-Gosálbez, G.; Sorribas, A.; Alves, R.; Jiménez, L. PGobal optimization of hybrid kinetic/FBA models via outer-approximation. Comput. Chem. Eng. 2015, 72, 325–333. [Google Scholar] [CrossRef]
- Wu, W.H.; Chien, C.Y.; Wu, Y.H.; Wu, H.H.; Lai, J.M.; Chang, P.M.H.; Huang, C.Y.F.; Wang, F.S. Inferring oncoenzymes in a genome-scale metabolic network for hepatocytes using bilevel optimization framework. J. Taiwan Inst. Chem. Eng. 2018, 91, 97–104. [Google Scholar] [CrossRef]
- Hsu, K.C.; Wang, F.S. Detection of minimum biomarker features via bi-level optimization framework by nested hybrid differential evolution. J. Taiwan Inst. Chem. Eng. 2017, 81, 31–39. [Google Scholar] [CrossRef]
- Bauer, G. Tumor cell-protective catalase as a novel target for rational therapeutic approaches based on specific intercellular ROS signaling. Anticancer Res. 2012, 32, 2599–2624. [Google Scholar] [PubMed]
- Glorieux, C.; Calderon, P.B. Catalase, a remarkable enzyme: Targeting the oldest antioxidant enzyme to find a new cancer treatment approach. Biol. Chem. 2017, 398, 1095–1108. [Google Scholar] [CrossRef] [Green Version]
- Glorieux, C.; Zamocky, M.; Sandoval, J.M.; Verrax, J.; Calderon, P.B. Regulation of catalase expression in healthy and cancerous cells. Free Radical Biol. Med. 2015, 87, 84–97. [Google Scholar] [CrossRef]
- Ma, Y.T.; Xing, X.F.; Dong, B.; Cheng, X.J.; Guo, T.; Du, H.; Wen, X.Z.; Ji, J.F. Higher autocrine motility factor/glucose-6-phosphate isomerase expression is associated with tumorigenesis and poorer prognosis in gastric cancer. Cancer Manag. Res. 2018, 10, 4969–4980. [Google Scholar] [CrossRef] [Green Version]
- Uzozie, A.C.; Selevsek, N.; Wahlander, A.; Nanni, P.; Grossmann, J.; Weber, A.; Buffoli, F.; Marra, G. Targeted proteomics for multiplexed verification of markers of colorectal tumorigenesis. Mol. Cell. Proteom. MCP 2017, 16, 407–427. [Google Scholar] [CrossRef] [Green Version]
- Pang, J.; Liu, W.P.; Liu, X.P.; Li, L.Y.; Fang, Y.Q.; Sun, Q.P.; Liu, S.J.; Li, M.T.; Su, Z.L.; Gao, X. Profiling Protein markers associated with lymph node metastasis in prostate cancer by DIGE-based proteomics analysis. J. Proteome Res. 2010, 9, 216–226. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Qin, L.; Li, B.; Liao, Z.; Liang, J.; Xiao, X.; Xiao, X.; Mo, Y.; Huang, G.; Zhang, Z.; et al. Inactivation of HMGCL promotes proliferation and metastasis of nasopharyngeal carcinoma by suppressing oxidative stress. Sci. Rep. 2017, 7, 11954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kjersem, J.B.; Thomsen, M.; Guren, T.; Hamfjord, J.; Carlsson, G.; Gustavsson, B.; Ikdahl, T.; Indrebø, G.; Pfeiffer, P.; Lingjærde, O.; et al. AGXT and ERCC2 polymorphisms are associated with clinical outcome in metastatic colorectal cancer patients treated with 5-FU/oxaliplatin. Pharmacogenom. J. 2015, 16, 272–279. [Google Scholar] [CrossRef] [PubMed]
- Pedro, N.F.; Biselli, J.M.; Maniglia, J.V.; Santi-Neto, D.D.; Pavarino, É.C.; Goloni-Bertollo, E.M.; Biselli-Chicote, P.M. Candidate biomarkers for oral squamous cell carcinoma: Differential expression of oxidative stress-related genes. Asian Pac. J. Cancer Prev. APJCP 2018, 19, 1343–1349. [Google Scholar]
- Cramer, S.D.; Ferree, P.M.; Lin, K.; Milliner, D.S.; Holmes, R.P. The gene encoding hydroxypyruvate reductase (GRHPR) is mutated in patients with primary hyperoxaluria type II. Hum. Mol. Genet. 1999, 8, 2063–2069. [Google Scholar] [CrossRef] [Green Version]
- Ju, H.Q.; Lu, Y.X.; Wu, Q.N.; Liu, J.; Zeng, Z.L.; Mo, H.Y.; Chen, Y.; Tian, T.; Wang, Y.; Kang, T.B.; et al. Disrupting G6PD-mediated Redox homeostasis enhances chemosensitivity in colorectal cancer. Oncogene 2017, 36, 6282–6292. [Google Scholar] [CrossRef] [Green Version]
- Buj, R.; Aird, K.M. Deoxyribonucleotide triphosphate metabolism in cancer and metabolic disease. Front. Endocrinol. 2018, 9, 177. [Google Scholar] [CrossRef]
- Marini, C.; Ravera, S.; Buschiazzo, A.; Bianchi, G.; Orengo, A.M.; Bruno, S.; Bottoni, G.; Emionite, L.; Pastorino, F.; Monteverde, E.; et al. Discovery of a novel glucose metabolism in cancer: The role of endoplasmic reticulum beyond glycolysis and pentose phosphate shunt. Sci. Rep. 2016, 6, 25092. [Google Scholar] [CrossRef] [Green Version]
- Tsachaki, M.; Mladenovic, N.; Štambergová, H.; Birk, J.; Odermatt, A. Hexose-6-phosphate dehydrogenase controls cancer cell proliferation and migration through pleiotropic effects on the unfolded-protein response, calcium homeostasis, and redox balance. FASEB J. Off. Publ. Fed. Am. Soc. Exp. Biol. 2018, 32, 2690–2705. [Google Scholar] [CrossRef] [Green Version]
- Harami-Papp, H.; Pongor, L.S.; Munkácsy, G.; Horváth, G.; Nagy, Á.M.; Ambrus, A.; Hauser, P.; Szabó, A.; Tretter, L.; Győrffy, B. TP53 mutation hits energy metabolism and increases glycolysis in breast cancer. Oncotarget 2016, 7, 67183–67195. [Google Scholar] [CrossRef] [Green Version]
- Yeshayahu, Y.; Asaf, R.; Dubnov-Raz, G.; Schiby, G.; Simon, A.J.; Lev, A.; Somech, R. Testicular failure in a patient with G6PC3 deficiency. Pediatr. Res. 2014, 76, 197–201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donnard, E.; Asprino, P.F.; Correa, B.R.; Bettoni, F.; Koyama, F.C.; Navarro, F.C.P.; Perez, R.O.; Mariadason, J.; Sieber, O.M.; Strausberg, R.L.; et al. Mutational analysis of genes coding for cell surface proteins in colorectal cancer cell lines reveal novel altered pathways, druggable mutations and mutated epitopes for targeted therapy. Oncotarget 2014, 5, 9199–9213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aust, S.; Brucker, B.; Graf, J.; Klimpfinger, M.; Thalhammer, T. Melatonin modulates acid/base transport in human pancreatic carcinoma cells. Cell. Physiol. Biochem. 2006, 18, 91–102. [Google Scholar] [CrossRef]
- Cappello, A.R.; Curcio, R.; Lappano, R.; Maggiolini, M.; Dolce, V. The physiopathological role of the exchangers belonging to the SLC37 family. Front. Chem. 2018, 6, 122. [Google Scholar] [CrossRef] [PubMed]
- Parks, S.K.; Cormerais, Y.; Durivault, J.; Pouyssegur, J. Genetic disruption of the pHi-regulating proteins Na+/H+ exchanger 1 (SLC9A1) and carbonic anhydrase 9 severely reduces growth of colon cancer cells. Oncotarget 2017, 8, 10225–10237. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Luo, L.; Begum, G.; Kohanbash, G.; Song, Q.; Rao, A.; Amankulor, N.; Sun, B.; Sun, D.; Jia, W. Elevated Na/H exchanger 1 (SLC9A1) emerges as a marker for tumorigenesis and prognosis in gliomas. J. Exp. Clin. Cancer Res. 2018, 37, 255. [Google Scholar] [CrossRef] [Green Version]
- Yizhak, K.; Gaude, E.; Le Dévédec, S.; Waldman, Y.Y.; Stein, G.Y.; van de Water, B.; Frezza, C.; Ruppin, E. Phenotype-based cell-specific metabolic modeling reveals metabolic liabilities of cancer. eLife 2014, 3, e03641. [Google Scholar] [CrossRef] [Green Version]
- Elia, I.; Broekaert, D.; Christen, S.; Boon, R.; Radaelli, E.; Orth, M.F.; Verfaillie, C.; Grünewald, T.G.P.; Fendt, S.M. Proline metabolism supports metastasis formation and could be inhibited to selectively target metastasizing cancer cells. Nat. Commun. 2017, 8, 15267. [Google Scholar] [CrossRef]
- Tang, L.; Zeng, J.; Geng, P.; Fang, C.; Wang, Y.; Sun, M.; Wang, C.; Wang, J.; Yin, P.; Hu, C.; et al. Global metabolic profiling identifies a pivotal role of proline and hydroxyproline metabolism in supporting hypoxic response in hepatocellular carcinoma. Clin. Cancer Res. 2018, 24, 474–485. [Google Scholar] [CrossRef] [Green Version]
- Huang, F.; Ni, M.; Chalishazar, M.D.; Huffman, K.E.; Kim, J.; Cai, L.; Shi, X.; Cai, F.; Zacharias, L.G.; Ireland, A.S.; et al. Inosine monophosphate dehydrogenase dependence in a subset of small cell lung cancers. Cell Metab. 2018, 28, 369–382.e5. [Google Scholar] [CrossRef] [Green Version]
- Rychtarcikova, Z.; Lettlova, S.; Tomkova, V.; Korenkova, V.; Langerova, L.; Simonova, E.; Zjablovskaja, P.; Alberich-Jorda, M.; Neuzil, J.; Truksa, J. Tumor-initiating cells of breast and prostate origin show alterations in the expression of genes related to iron metabolism. Oncotarget 2017, 8, 6376–6398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vedeld, H.M.; Andresen, K.; Eilertsen, I.A.; Nesbakken, A.; Seruca, R.; Gladhaug, I.P.; Thiis-Evensen, E.; Rognum, T.O.; Boberg, K.M.; Lind, G.E. The novel colorectal cancer biomarkers CDO1, ZSCAN18 and ZNF331 are frequently methylated across gastrointestinal cancers. Int. J. Cancer 2015, 136, 844–853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ooki, A.; Maleki, Z.; Tsay, J.C.J.; Goparaju, C.; Brait, M.; Turaga, N.; Nam, H.S.; Rom, W.N.; Pass, H.I.; Sidransky, D.; et al. A panel of novel detection and prognostic methylated DNA markers in primary non-small cell lung cancer and serum DNA. Clin. Cancer Res. 2017, 23, 7141–7152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weidle, U.H.; Birzele, F.; Kruger, A. Molecular targets and pathways involved in liver metastasis of colorectal cancer. Clin. Exp. Metastasis 2015, 32, 623–635. [Google Scholar] [CrossRef]
- Galluzzi, L.; Goubar, A.; Olaussen, K.A.; Vitale, I.; Senovilla, L.; Michels, J.; Robin, A.; Dorvault, N.; Besse, B.; Validire, P.; et al. Prognostic value of LIPC in non-small cell lung carcinoma. Cell Cycle 2013, 12, 647–654. [Google Scholar] [CrossRef] [Green Version]
- Szklarczyk, D.; Morris, J.H.; Cook, H.; Kuhn, M.; Wyder, S.; Simonovic, M.; Santos, A.; Doncheva, N.T.; Roth, A.; Bork, P.; et al. The STRING database in 2017: Quality-controlled protein-protein association networks, made broadly accessible. Nucleic Acids Res. 2017, 45, D362–D368. [Google Scholar] [CrossRef]
- Firestein, R.; Bass, A.J.; Kim, S.Y.; Dunn, I.F.; Silver, S.J.; Guney, I.; Freed, E.; Ligon, A.H.; Vena, N.; Ogino, S.; et al. CDK8 is a colorectal cancer oncogene that regulates β-catenin activity. Nature 2008, 455, 547–551. [Google Scholar] [CrossRef]







| Gene | Pathway | Ave. CR | Ave. SR | p Value | Disease (Score) | Remark |
|---|---|---|---|---|---|---|
| CAT | Ethanol degradation | 0.934 | 0.982 | 1.46 | Gonadoblastoma (1.42) Amelanotic Melanoma (1.39) | Related to ROS signaling pathway [38,39,40]. |
| GPI | Pentose phosphate pathway | 0.931 | 0.981 | 6.57 | Fibrosarcoma (1.08) | Gastric cancer [41]. |
| PPA2 | TRNA aminoacylation | 0.935 | 0.982 | 0.4926 | Sudden Cardiac Failure, Infantile (2.83) | Colorectal cancer [42] Prostate cancer [43]. |
| HMGCL | Ketone body metabolism | 0.935 | 0.982 | 3.8 | 3-Hydroxy-3-Methylglutaryl-Coa Lyase Deficiency (2.83) | Nasopharyngeal carcinoma [44]. |
| AGXT | Alanine and aspartate metabolism | 0.933 | 0.982 | 0.0133 | Hyperoxaluria, Primary, Type I (2.83) | Colorectal cancer [45]. |
| GLRX2 | PAK pathway | 0.932 | 0.982 | 4.35 | NA | Oral squamous cell carcinoma [46]. |
| GRHPR | Glyoxylate metabolism and glycine degradation | 0.934 | 0.982 | 0.0018 | Hyperoxaluria, Primary, Type Ii (2.83) | Hyperoxaluria [47]. |
| G6PD | Methylene blue pathway | 0.827 | 0.980 | 1.37 | Anemia (2.63) Glutathione Synthetase Deficiency (1.50) | Colorectal cancer [48] Obesity and diabetes [49]. |
| H6PD | Pentose phosphate pathway | 0.918 | 0.982 | 0.0018 | Cortisone Reductase Deficiency 1 (2.83) | Cancer cell lines for colon, breast and lung [50,51]. |
| G6PC3 | Carbohydrate digestion and absorption | 0.936 | 0.982 | 4.55 | Albinism, Oculocutaneous, Type Iv (1.26) | Breast cancer [52] Neutropenia [53]. |
| SLC26A6 | Mineral absorption | 0.934 | 0.982 | 0.8577 | Inflammatory Diarrhea (1.50) | Colorectal cancer cell lines [54] Pancreatic cancer cell [55]. |
| SLC37A4 | Carbohydrate digestion and absorption | 0.930 | 0.982 | 0.4026 | Glycogen Storage Disease (2.83) Pancreatic Ductal Adenocarcinoma (0.43) | Congenital hyperinsulinism of infancy [56]. |
| SLC9A1 | Osteoclast signaling | 0.932 | 0.982 | 1.9 | Lichtenstein-Knorr Syndrome (2.83) Breast Cancer (0.38) | Colon cancer cells [57] Gliomas [58]. |
| MLYCD | Peroxisomal lipid metabolism | 0.933 | 0.982 | 1.84 | Malonyl-Coa Decarboxylase Deficiency (2.83) Pain-Chronic (1.43) | Proliferation of cancer cell lines [59]. |
| PYCR3 | Urea cycle and metabolism of amino groups | 0.934 | 0.982 | 3.44 | Lung Cancer Susceptibility (0.42) | Related to metastasis of cancer cells [60]. |
| PRODH2 | Arginine and proline metabolism | 0.933 | 0.981 | 4.2 | Primary Hyperoxaluria (1.34) | Hepatocellular carcinoma [61]. |
| IMPDH1 | Nucleotide metabolism | 0.934 | 0.982 | 8.81 | Leber Congenital Amaurosis (2.83) | Small cell lung cancer [62]. |
| CYBRD1 | Mineral absorption | 0.934 | 0.981 | 0.0013 | Iron Metabolism Disease (1.36) | Breast and prostate cancer cells [63]. |
| CDO1 | Taurine and hypotaurine metabolism | 0.934 | 0.982 | 1.08 | Small Intestine Cancer (1.31) | Colorectal cancer [64] Non-small cell lung cancer [65]. |
| LIPC | Triacylglycerol degradation | 0.940 | 0.981 | 0.0319 | Hepatic Lipase Deficiency (2.83) | Colorectal cancer [66] Non-small cell lung carcinoma [67]. |
| Reaction | Gene | Other Regulated Reactions | Isozyme | Ave. CR | Ave. SR | Remark |
|---|---|---|---|---|---|---|
| GPI | GPI | – | – | 0.931 | 0.981 | Gastric cancer [41]. |
| r0161 | AGXT | – | – | 0.933 | 0.982 | Colorectal cancer [45]. |
| r0249 | RPIA | RPI | – | 0.935 | 0.981 | Overestimated. |
| HMGLx | HMGCL | HMGLx | HMGCLL1 | 0.934 | 0.982 | Nasopharyngeal carcinoma [44]. |
| r0616 | PRODH2 | PROD2, r0615, PRO1x | – | 0.934 | 0.982 | Hepatocellular carcinoma [61]. |
| CATp | CAT | CATPm, r0010 | – | 0.932 | 0.982 | Related to ROS signaling [38,39,40]. |
| CATm | CAT | CATp, r0010 | – | 0.838 | 0.979 | Underestimated, ROS signaling [38,39,40]. |
| r0010 | CAT | CATm, CATp | – | 0.867 | 0.981 | Underestimated, ROS signaling [38,39,40]. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.-S.; Wu, W.-H.; Hsiu, W.-S.; Liu, Y.-J.; Chuang, K.-W. Genome-Scale Metabolic Modeling with Protein Expressions of Normal and Cancerous Colorectal Tissues for Oncogene Inference. Metabolites 2020, 10, 16. https://doi.org/10.3390/metabo10010016
Wang F-S, Wu W-H, Hsiu W-S, Liu Y-J, Chuang K-W. Genome-Scale Metabolic Modeling with Protein Expressions of Normal and Cancerous Colorectal Tissues for Oncogene Inference. Metabolites. 2020; 10(1):16. https://doi.org/10.3390/metabo10010016
Chicago/Turabian StyleWang, Feng-Sheng, Wu-Hsiung Wu, Wei-Shiang Hsiu, Yan-Jun Liu, and Kuan-Wei Chuang. 2020. "Genome-Scale Metabolic Modeling with Protein Expressions of Normal and Cancerous Colorectal Tissues for Oncogene Inference" Metabolites 10, no. 1: 16. https://doi.org/10.3390/metabo10010016
APA StyleWang, F. -S., Wu, W. -H., Hsiu, W. -S., Liu, Y. -J., & Chuang, K. -W. (2020). Genome-Scale Metabolic Modeling with Protein Expressions of Normal and Cancerous Colorectal Tissues for Oncogene Inference. Metabolites, 10(1), 16. https://doi.org/10.3390/metabo10010016