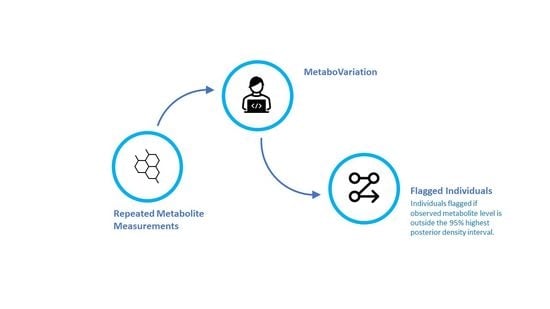
MetaboVariation: Exploring Individual Variation in Metabolite Levels
Abstract
:1. Introduction
2. Materials and Methods
2.1. The MetaboVariation Method
2.2. Simulation Study Design
3. Results
3.1. Simulation Study
3.2. Case Study: Fasting Plasma Samples from A-Diet Confirm Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, Y.; Chen, L.; Li, X.S.; Li, X.L.; Xu, X.D.; Tai, S.B.; Yang, G.L.; Tang, Q.; Liu, H.; Liu, S.H.; et al. Metabolomic Identification of Exosome-Derived Biomarkers for Schizophrenia: A Large Multicenter Study. Schizophr. Bull. 2021, 47, 615–623. [Google Scholar] [CrossRef] [PubMed]
- Eroglu, E.C.; Tunug, S.; Geckil, O.F.; Gulec, U.K.; Vardar, M.A.; Paydas, S. Discovery of metabolomic biomarkers for discriminating platinum-sensitive and platinum-resistant ovarian cancer by using GC-MS. Eur. J. Mass Spectrom. 2021, 27, 235–248. [Google Scholar] [CrossRef] [PubMed]
- Kalhan, S.C.; Guo, L.; Edmison, J.; Dasarathy, S.; McCullough, A.J.; Hanson, R.W.; Milburn, M. Plasma metabolomic profile in nonalcoholic fatty liver disease. Metab. Clin. Exp. 2011, 60, 404–413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dambrova, M.; Makrecka-Kuka, M.; Kuka, J.; Vilskersts, R.; Nordberg, D.; Attwood, D.; Attwood, M.M.; Smesny, S.; Sen, Z.D.; Guo, A.C.; et al. Acylcarnitines: Nomenclature, Biomarkers, Therapeutic Potential, Drug Targets, and Clinical Trials. Am. Soc. Pharmacol. Exp. Ther. 2022, 74, 506–551. [Google Scholar] [CrossRef]
- Ramzan, I.; Ardavani, A.; Vanweert, F.; Mellett, A.; Atherton, P.J.; Idris, I. The Association between Circulating Branched Chain Amino Acids and the Temporal Risk of Developing Type 2 Diabetes Mellitus: A Systematic Review and Meta-Analysis. Nutrients 2022, 14, 4411. [Google Scholar] [CrossRef]
- Merino, J. Precision nutrition in diabetes: When population-based dietary advice gets personal. Diabetologia 2022, 65, 1839–1848. [Google Scholar] [CrossRef]
- Jardon, K.M.; Canfora, E.E.; Goossens, G.H.; Blaak, E.E. Dietary macronutrients and the gut microbiome: A precision nutrition approach to improve cardiometabolic health. Gut 2022, 71, 1214–1226. [Google Scholar] [CrossRef]
- Chaleckis, R.; Murakami, I.; Takada, J.; Kondoh, H.; Yanagida, M. Individual variability in human blood Metabolites identifies age-related differences. Proc. Natl. Acad. Sci. USA 2016, 113, 4252–4259. [Google Scholar] [CrossRef] [Green Version]
- Guida, F.; Tan, V.Y.; Corbin, L.J.; Smith-Byrne, K.; Alcala, K.; Langenberg, C.; Stewart, I.D.; Butterworth, A.S.; Surendran, P.; Achaintre, D.; et al. The blood metabolome of incident kidney cancer: A case-control study nested within the MetKid consortium. PLoS Med. 2021, 18, e1003786. [Google Scholar] [CrossRef]
- Imamura, F.; Fretts, A.; Marklund, M.; Ardisson Korat, A.V.; Yang, W.S.; Lankinen, M.; Qureshi, W.; Helmer, C.; Chen, T.A.; Wong, K.; et al. Fatty acid biomarkers of dairy fat consumption and incidence of type 2 diabetes: A pooled analysis of prospective cohort studies. PLoS Med. 2018, 15, e1002670. [Google Scholar] [CrossRef] [Green Version]
- Jansen, J.J.; Szymańska, E.; Hoefsloot, H.C.J.; Smilde, A.K. Individual differences in metabolomics: Individualised responses and between-metabolite relationships. Metabolomics 2012, 8, 94–104. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Mias, G.I.; Li-Pook-Than, J.; Jiang, L.; Lam, H.Y.; Chen, R.; Miriami, E.; Karczewski, K.J.; Hariharan, M.; Dewey, F.E.; et al. Personal omics profiling reveals dynamic molecular and medical phenotypes. Cell 2012, 148, 1293–1307. [Google Scholar] [CrossRef] [Green Version]
- Piening, B.D.; Zhou, W.; Contrepois, K.; Röst, H.; Gu Urban, G.J.; Mishra, T.; Hanson, B.M.; Bautista, E.J.; Leopold, S.; Yeh, C.Y.; et al. Integrative Personal Omics Profiles during Periods of Weight Gain and Loss. Cell Syst. 2018, 10, 2405–4712. [Google Scholar] [CrossRef]
- McFarquhar, M. Modeling Group-Level Repeated Measurements of Neuroimaging Data Using the Univariate General Linear Model. Front. Neurosci. 2019, 13, 352. [Google Scholar] [CrossRef] [Green Version]
- Hadfield, J.D. MCMC Methods for Multi-Response Generalized Linear Mixed Models: The MCMCglmm R Package. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis Third Edition (With Errors Fixed as of 13 February 2020); CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Yin, X.; Prendiville, O.; McNamara, A.; Brennan, L. Targeted Metabolomic Approach to Assess the Reproducibility of Plasma Metabolites over a Four Month Period in a Free-Living Population. J. Proteome Res. 2022, 21, 683–690. [Google Scholar] [CrossRef]
- Prendiville, O.; Walton, J.; Flynn, A.; Nugent, A.P.; McNulty, B.A.; Brennan, L. Classifying Individuals Into a Dietary Pattern Based on Metabolomic Data. Mol. Nutr. Food Res. 2021, 65, e2001183. [Google Scholar] [CrossRef]
- J Stewart–Knox, B.; Rankin, A.; P Bunting, B.; J Frewer, L.; Celis-Morales, C.; M Livingstone, K.; Fischer, A.R.H.; Poínhos, R.; Kuznesof, S.; J Gibney, M.; et al. Self-efficacy, habit strength, health locus of control and response to the personalised nutrition Food4Me intervention study. Br. Food J. 2022, 124, 314–330. [Google Scholar] [CrossRef]
- Dello Russo, M.; Russo, P.; Rufián-Henares, J.Á.; Hinojosa-Nogueira, D.; Pérez-Burillo, S.; de la Cueva, S.P.; Rohn, S.; Fatouros, A.; Douros, K.; González-Vigil, V.; et al. The Stance4Health Project: Evaluating a Smart Personalised Nutrition Service for Gut Microbiota Modulation in Normal- and Overweight Adults and Children with Obesity, Gluten-Related Disorders or Allergy/Intolerance to Cow’s Milk. Foods 2022, 11, 1480. [Google Scholar] [CrossRef]
- Wilson-Barnes, S.; Hart, K.; Gymnopoulos, L.P.; Dimitropoulos, K.; Solachidis, V.; Rouskas, K.; Russell, D.; Oikonomidis, I.; Hadjidimitriou, S.; Botana, J.M.; et al. Personalised Nutrition for Healthy Living: The PROTEIN Project. Nutr. Bull. 2021, 46, 77–87. [Google Scholar] [CrossRef]
- San-Cristobal, R.; Navas-Carretero, S.; Celis-Morales, C.; Livingstone, K.M.; Stewart-Knox, B.; Rankin, A.; Macready, A.L.; Fallaize, R.; O’Donovan, C.B.; Forster, H.; et al. Capturing health and eating status through a nutritional perception screening questionnaire (NPSQ9) in a randomised internet-based personalised nutrition intervention: The Food4Me study. Int. J. Behav. Nutr. Phys. Act. 2017, 14, 168. [Google Scholar] [CrossRef]
- Livingstone, K.M.; Celis-Morales, C.; Navas-Carretero, S.; San-Cristobal, R.; Forster, H.; Woolhead, C.; O’Donovan, C.B.; Moschonis, G.; Manios, Y.; Traczyk, I.; et al. Characteristics of participants who benefit most from personalised nutrition: Findings from the pan-European Food4Me randomised controlled trial. Br. J. Nutr. 2020, 123, 1396–1405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brennan, L.; De Roos, B. Nutrigenomics: Lessons learned and future perspectives. Am. J. Clin. Nutr. 2021, 113, 503–516. [Google Scholar] [CrossRef] [PubMed]
- Pusparum, M.; Ertaylan, G.; Thas, O. Individual reference intervals for personalised interpretation of clinical and metabolomics measurements. J. Biomed. Inform. 2022, 131, 104111. [Google Scholar] [CrossRef]
- Pusparum, M.; Ertaylan, G.; Thas, O. From Population to Subject-Specific Reference Intervals. In Proceedings of the Computational Science—ICCS 2020, Amsterdam, The Netherlands, 3–5 June 2020; Krzhizhanovskaya, V.V., Závodszky, G., Lees, M.H., Dongarra, J.J., Sloot, P.M.A., Brissos, S., Teixeira, J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 468–482. [Google Scholar]
- Carayol, M.; Licaj, I.; Achaintre, D.; Sacerdote, C.; Vineis, P.; Key, T.J.; Onland Moret, N.C.; Scalbert, A.; Rinaldi, S.; Ferrari, P. Reliability of Serum Metabolites over a Two-Year Period: A Targeted Metabolomic Approach in Fasting and Non-Fasting Samples from EPIC. PLoS ONE 2015, 10, e0135437. [Google Scholar] [CrossRef] [Green Version]
- Floegel, A.; Drogan, D.; Wang-Sattler, R.; Prehn, C.; Illig, T.; Adamski, J.; Joost, H.G.; Boeing, H.; Pischon, T. Reliability of serum metabolite concentrations over a 4-month period using a targeted metabolomic approach. PLoS ONE 2011, 6, e21103. [Google Scholar] [CrossRef]



| Metabolite | Sex | Age | BMI |
|---|---|---|---|
| Ala | −4.41 (−26.17, 17.41) | −0.57 (−1.35, 0.2) | 2.65 (−0.69, 5.95) |
| Arg | −5.49 (−10.35, −0.65) | 0.19 (0.01, 0.37) | −0.64 (−1.41, 0.14) |
| Asn | −1.32 (−4.8, 2.17) | −0.16 (−0.28, −0.03) | −0.27 (−0.82, 0.29) |
| Cit | −3.82 (−5.81, −1.77) | 0.13 (0.05, 0.2) | −0.3 (−0.61, 0.02) |
| Gln | −38.53 (−61.06, −16.57) | 1.57 (0.79, 2.36) | −3.03 (−6.46, 0.46) |
| Glu | −8.38 (−13.07, −3.73) | 0.26 (0.1, 0.43) | 1.35 (0.63, 2.08) |
| Gly | 15.45 (−9.12, 40.1) | 0.95 (0.06, 1.85) | −2.61 (−6.51, 1.34) |
| His | -0.89 (−4.26, 2.56) | −0.06 (−0.18, 0.06) | 0.37 (−0.17, 0.89) |
| Ile | −19.65 (−23.48, −15.77) | −0.26 (−0.4, −0.12) | 0.79 (0.19, 1.37) |
| Leu | −40.57 (−47.84, −33.33) | −0.27 (−0.53, −0.02) | 1.71 (0.57, 2.87) |
| Lys | -8.88 (−17.9, 0.12) | 0.36 (0.03, 0.69) | −0.54 (−1.92, 0.86) |
| Met | −2.92 (−4.14, −1.7) | −0.04 (−0.09, 0) | 0.01 (−0.18, 0.2) |
| Orn | −9.88 (−13.94, −5.88) | 0.29 (0.15, 0.44) | −0.83 (−1.45, −0.21) |
| Phe | −6.19 (−9.23, −3.1) | −0.11 (−0.22, 0) | 0.35 (−0.13, 0.81) |
| Pro | −37.61 (−53.97, −21.57) | −0.37 (−0.95, 0.2) | 2.37 (−0.22, 4.91) |
| Ser | 7.51 (0.17, 14.86) | −0.15 (−0.41, 0.11) | −0.87 (−1.99, 0.25) |
| Thr | 4.06 (−3.8, 11.91) | −0.34 (−0.62, −0.06) | −0.38 (−1.6, 0.8) |
| Trp | −8.06 (−11.12, −4.95) | −0.17 (−0.29, −0.06) | 0.33 (−0.17, 0.81) |
| Tyr | −5.33 (−9.31, −1.4) | 0.07 (−0.08, 0.21) | 0.95 (0.33, 1.57) |
| Val | −34.47 (−43.8, −25.42) | −0.06 (−0.41, 0.27) | 1.21 (−0.25, 2.64) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, S.; Gormley, I.C.; Brennan, L. MetaboVariation: Exploring Individual Variation in Metabolite Levels. Metabolites 2023, 13, 164. https://doi.org/10.3390/metabo13020164
Gupta S, Gormley IC, Brennan L. MetaboVariation: Exploring Individual Variation in Metabolite Levels. Metabolites. 2023; 13(2):164. https://doi.org/10.3390/metabo13020164
Chicago/Turabian StyleGupta, Shubbham, Isobel Claire Gormley, and Lorraine Brennan. 2023. "MetaboVariation: Exploring Individual Variation in Metabolite Levels" Metabolites 13, no. 2: 164. https://doi.org/10.3390/metabo13020164
APA StyleGupta, S., Gormley, I. C., & Brennan, L. (2023). MetaboVariation: Exploring Individual Variation in Metabolite Levels. Metabolites, 13(2), 164. https://doi.org/10.3390/metabo13020164