1. Introduction
The comprehensive detection and quantification of metabolites in biological systems, coined as ‘metabolomics’, offers a new approach to interrogate mechanistic biochemistry related to natural processes such as health and disease. Recent developments in mass spectrometry (MS) and nuclear magnetic resonance (NMR) have been crucial to facilitate the global analysis of metabolites. The examination of metabolites, however, commonly follows two strategies: (i) targeted metabolomics, driven by a specific biochemical question or hypothesis in which a set of metabolites related to one or more pathways are defined, or (ii) untargeted metabolomics: driven by an unbiased approach (
i.e., non-hypothesis) in which as many metabolites as possible are measured and compared between samples [
1]. The latter is comprehensive in scope and outputs complex data sets, particularly by using LC/MS-based methods. Thousands of so called metabolite features (
i.e., peaks corresponding to individual ions with a unique mass-to-charge ratio and a unique retention time or mzRT features from now on) can be routinely detected in biological samples. In addition, each mzRT feature in the dataset is associated with an intensity value (or area under the peak), which indicates its relative abundance in the sample. Overall, this complexity imposes the implementation of metabolomic softwares such as XCMS [
2], MZmine [
3] or Metalign [
4] that can provide automatic methods for peak picking, retention time alignment to correct experimental drifts in instrumentation, and relative quantification. As a result, the identification of mzRT features that are differentially altered between sample groups has become a relatively automated process. However, the identification and quantization of a “metabolite feature” does not necessary translate into a metabolite entity. LC/MS metabolomic data presents high redundancy because of the recurrent detection of adducts (Na+, K+, NH3, etc), isotopes, or doubly charged ions that greatly inflate the number of detected peaks. Several recently launched open-source algorithms such as CAMERA [
5] or AStream [
6], and commercially available software such as Mass Hunter (Agilent Technologies) or Sieve (Thermo Scientific), are capable of filtering redundancy by annotating isotopes and adduct peaks, and the resulting accurate compound mass (
i.e., molecular ion) can be searched in metabolite databases such as METLIN, HMDB or KEGG. Database matching represents only a putative metabolite assignment that must be confirmed by comparing the retention time and/or MS/MS data of a model pure compound to that from the feature of interest in the research sample. These additional analyses are time consuming and represent the rate-limiting step of the untargeted metabolomic workflow. Consequently, it is essential to prioritize the list of mzRT features from the raw data that will be subsequently identified by RT and/or MS/MS comparison. Relevant mzRT features for MS/MS identification are typically selected based on statistics criteria, either by multivariate data analysis or multiple independent univariate tests.
The intrinsic nature of biological processes and LC/MS-derived datasets is undoubtedly multivariate since it involves observation and analysis of more than one variable at a time. Consequently, the majority of metabolomics studies make use of multivariate models to report their main findings. Despite the conferred utility, powerfulness and versatility of multivariate models, their performance might be fraught by the high-dimensionality of such datasets due to the so-called ‘curse of dimensionality’ problem. Curse of dimensionality arises when datasets contain too much sparse data in terms of the number of input variables. This causes, in a given sample size, a maximum number of variables above which the performance of our multivariate model will degrade rather than improve. Hence, attempting to make the model conform too closely to this data (
i.e., considering too many variables in our multivariate model) can introduce substantial errors and reduce its predictive power (
i.e., overfitting). Therefore, using multivariate models require intensive validation work. Overall, multivariate data analysis is far from the scope of this paper and excellent reviews on multivariate tools for metabolomics can be found elsewhere [
7,
8]. On the other hand, data analysis can also be approached from a univariate perspective using traditional statistical methods that consider only one variable at a time [
9]. The implementation of multivariate and univariate data analysis is not mutually exclusive and in fact, we strongly recommend their combined use to maximize the extraction of relevant information from metabolomic datasets [
10,
11]. Univariate methods are sometimes used in combination with multivariate models as a filter to retain those potentially “information-rich” mzRT features [
12]. Then, the number of mzRT features considered in the multivariate model is significantly reduced down to those showing statistical significance in previous univariate tests (e.g., p-value < 0.05). On the other hand, there are multiple reported metabolomics works using univariate tests applied in parallel across all the detected mzRT features to report their main findings. It should be note that this approach overlooks correlations within mzRT features and therefore information about correlated trends is not retained. In addition, applying multiple univariate tests in parallel to multivariate datasets involves the acceptance of mathematical pre-requisites and certain consequences such as the particular distributions of variables (e.g., normality) and increased risk of false positive results, respectively. Many researchers often ignore these issues when analyzing untargeted metabolomic datasets using univariate methods, which eventually can compromise their results.
This paper aims to investigate the impact of univariate statistical issues on LC/MS-based metabolomic experiments, particularly in small, focused studies (e.g., small clinical trials or animal studies). To this end, here we explore the nature of four real and independent datasets, evaluate the challenges and limitations of executing multiple univariate tests and illustrate available shortcuts. Note that we do not aim at writing a conventional statistical paper. Instead, our goal is to offer a practical guide with resources to overcome the challenges of multiple univariate analysis for untargeted metabolomic data. All methods described in this paper are based on scripts programmed either in MATLAB™ (Mathworks, Natick, MA) or R [
13] .
2. Properties of LC-MS Untargeted Datasets: High-Dimensional and Multicolinear
Basic information about the four real untargeted metabolomics LC-MS-based working examples is summarized in
Table 1. These examples do not resemble ideal datasets described in basic statistical textbooks, and illustrates the challenges of real-life metabolomic experiments. Working examples constitute retinas, serum and neuronal cell cultures under different experimental conditions (e.g., KO
vs. WT; normoxia
vs. hypoxia; treated
vs. untreated) analyzed by LC-qTOF MS. Data were processed using the XCMS software to detect and align features, and thousands of features were generated from these biological samples. Each mzRT feature corresponds to a detected ion with a unique mass-to-charge ratio, retention time and raw intensity (or area). For example, each sample in example #3 exists in a space defined by 9877 variables or mzRT features. The four examples illustrate the high-dimensionality of untargeted LC-MS datasets in which the number of features or variables largely exceeds the number of samples. The rather limited number of individuals or samples per group is a common trait of metabolomic studies devoted to understand cellular metabolism [
14,
15,
16]. When working with animal models of disease, for instance, this limitation is typically imposed by ethical and economical restrictions.
Table 1.
Summary of working examples obtained from LC-MS untargeted metabolomic experiments. Further experimental details and methods can be obtained from references. (KO=Knock-Out; WT=Wild-Type).
| | Biofluid/Tissue | Sample groups | # samples /group | # XCMS variables | System | Reference |
|---|
| Example #1 | Retina | KO | 11 | 4581 | LC/ESI-QTOF | [17] |
| WT | 11 |
| Example #2 | Retina | Hypoxia | 12 | 8146 | LC/ESI-QTOF | [16] |
| Normoxia | 13 |
| Example #3 | Serum | Untreated | 12 | 9877 | LC/ESI-TOF | [18] |
| Treated | 12 |
| Example #4 | Neuronal cell cultures | KO | 15 | 8221 | LC/ESI-QTOF | unpublished data |
| WT | 11 |
Additionally, a second attribute of untargeted LC-MS metabolomic datasets is that they enclose multiple correlations among mzRT features (
i.e., multicollinearity) [
19]. Each metabolite produces more than one mzRT feature that result from isotopic distributions, potential adducts, and in-source fragmentation. Moreover, the evident biochemical interrelation among metabolites may also contribute to the multicollinearity. Namely, many metabolites participate in inter-connected enzymatic reactions and pathways (e.g., substrate and product; cofactors) and regulate enzymatic reactions (e.g., feed-back inhibition). Altogether, untargeted LC-MS metabolomics datasets are highly-dimensional and multicorrelated.
4. Handling Analytical Variation
The first issue that must be resolved before considering any univariate statistical test on LC/MS untargeted metabolomic data is analytical variation. Most common sources of analytical variation in LC-MS experiments are due to sample preparation, instrumental drifts caused by chromatographic columns and MS detectors, and errors caused in data processing [
23].
The ideal method to examine analytical variation is to analyze quality control (QC) samples, which will provide robust quality assurance of each detected mzRT feature [
24]. To this end, QC samples should be prepared by pooling aliquots of each individual sample and analyze them periodically throughout the sample work list. The performance of the analytical platform for each detected mzRT feature in real samples can be assessed by calculating the relative standard deviation of these features on pooled samples (CV
QC) according to formula Equation (1), where S and
X are respectively the standard deviation and the mean of each individual feature detected across the QC samples:
Likewise, the relative standard deviation of these features on study samples (CVT) can be defined according to formula Equation (2), where S and X are the standard deviation and mean respectively calculated for each mzRT feature across all study samples in the dataset.
The variation of QC samples around their mean (CV
QC) is expected to be low since they are replicates of the same pooled samples. Therefore Dunn
et al. [
24] have established a quality criteria by which any peak that presents a CV
QC > 20% is removed from the dataset and thus ignored in subsequent univariate data analyses. Red and green spots in
Figure 2 illustrate the CV
T and CV
QC frequencies distributions respectively for example #3 in which QC samples were measured. As expected, the highest percentage of mzRT features detected across QC samples present the lowest variation in terms of CV
QC (green line). Conversely, the highest percentage of the mzRT features detected across the study samples holds the highest variation in terms of CV
T (red line). Notice that the intersection of red and green lines is produced around the threshold proposed by Dunn
et al. [
24]. Additionally, other studies performed on cerebrospinal fluid, serum or liver QC extracts also reported around 20% of CV on experimental replicates [
25,
26].
On the other hand, it is common that the nature of some biological samples and their limited availability complicates the analysis of QC samples. This was the case of mouse retinas in examples #1 and #2. Under these circumstances, there are not consensus standard criteria on how to handle analytical variation. We partially circumvent this issue using the following argument: Provided that the total variation of a metabolite feature (CVT) can be expressed as a sum of biological variation (CVB ) and analytical variation (CVA) according to Equation (3), computed CVT should be at minimum larger than 20% (the most accepted analytical variation threshold) for a metabolite feature to comprise biological variation.
Therefore, when QC samples are not available we propose as rule of thumb to discard those features showing CV
T < 20% since biological variation is bellow analytical variation threshold.
Figure 2 shows the frequency distribution of CV
T for working examples #1,2 and #4 where QC samples were not available. According to our criteria, those mzRT features to the left of the threshold will hold more analytical than biological variation and should be conveniently removed from further statistical analysis. This surely results in a too broad criterion since it assumes that the analytical variation of all metabolites is similar, which is of course not accurate given that instrumental drifts do not affect all metabolites evenly. It should be beard in mind, however, that tightly regulated metabolites presenting low variation such as glucose will likely be missed according to a 20% CV
T cut-off criterion. Of mention, example #2 and example #4 show the higher and lower percentage of mzRT features with more than 50% CV
T respectively. Therefore, there is more intrinsic variation in example #2 than in example#4. Whether such variation relates to the phenomena under study remain to be ascertained using hypothesis testing.
Figure 2.
Comparison for our four working examples of the mzRT relative standard deviation (CV) frequency distributions calculated either across all the samples (CVT) or across QC samples (CVQC). Grey spots represent CVT for examples #1(◊), #2 (∆) and #4 (□) respectively. Green and red circles represent CVQC and CVT respectively for example #3. Blue line represents 20% CVT cut-off threshold established when QC samples are not available.
5. Hypothesis Testing
Untargeted metabolomics studies focused in this paper are aimed at the discovery of those metabolites that are varied between two populations (
i.e., KO
vs WT in examples #1 and 4 or treated
vs untreated in example #3). In this sort of studies, random sample data from the populations to be compared are obtained in form of mzRT features dataset. Then, we calculate a statisti
c value (usually
mean or
median) and use statistical inference to determine whether the observed differences in the median or mean of the two populations are due to the phenomena under study or to randomness. Statistical inference is the process of drawing statements or conclusions about a populations based on sample data in a way that the risk of error of such conclusions is specified. These conclusions are based on probabilities arisen from evidences given by sample data [
27].
To characterize those varied mzRT features, data sets are usually specified via hypothesis testing. Conventionally, we first postulate a null difference between the means/median of metabolic features detected in the populations under study by setting a null hypothesis (H0). Then, we specify the probability threshold for this null hypothesis to be rejected when in fact it is true. This threshold of probability called α is frequently set-up at 5% and it can be though as the probability of a false positive result or Type I error. Then, we use hypothesis testing to calculate the probability (p-value) of null hypothesis rejection. Whenever this p-value is bellow to this pre-defined threshold of probability (α), we reject the null hypothesis. On the other hand, when calculated p-values are larger than α we do not have enough evidence to reject this hypothesis and we fail to reject it. Note that null hypothesis can never be proven, instead null hypothesis is either rejected or failed to reject. Conceptually, the failure to reject the null hypothesis (failure to find difference between the means) does not directly translate in to accept or prove it (showing that there is no difference in reality).
A wide variety of univariate statistical tests to compare mean or medians are available. For a non-statistician it can be daunting to figure out which one is most appropriate to implement with an untargeted metabolomic design and dataset. Helpful guidelines in basic statistics books can be consulted [
27,
28]. As summarized in
Table 2, two important considerations should be taken in to account when deciding for a particular test. First one is the experimental design and second one data distribution.
Table 2.
Best suited statistical tests for datasets following normal distribution or far from the normal curve according to their experimental design.
| Experimental design | Normal distribution | Far from normal-curve |
|---|
| Compare Means | Compare Medians |
|---|
| Compare two unpaired groups | Unpaired t-test | Mann-Whitney |
| Compare two paired groups | Paired t-test | Wilcoxon signed-rank |
| Compare more than two unmatched groups | One-way ANOVA with multiple comparison | Kruskal-Wallis |
| Compare more than two matched groups | Repeated-measures ANOVA | Friedman |
Experimental design will depend on experimental conditions considered when the metabolomics study is designed. Once the experimental design is fixed, population distribution determines the type of the test. Depending on this distribution, there are essentially two families of tests: parametric and non-parametric. Parametric tests are based on the assumption that data are sampled from a Gaussian or normal distribution. Tests that do not make assumptions about the population distribution are referred as to non-parametric tests. Selection of parametric or non-parametric tests is not as clear-cut as might be a priori though. Next section deals with the calculations necessary to guide such decision and exemplifies these calculations with our four working examples.
6. Deciding between Parametric or Non-Parametric Tests
6.1. Normality, Homogeneity of Variances and Independence Assumptions
Deciding between parametric and non-parametric tests should be based on three assumptions that should be checked: normality, homogeneity of variances (i.e., homocedasticity) and independence. Nevertheless, some of these assumptions rely on very theoretical mathematical constructs hardly ever met by real-life datasets obtained from metabolomics experiments.
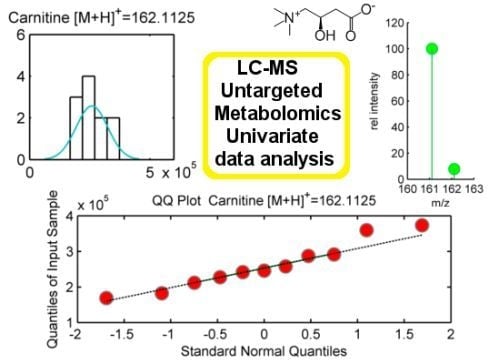
Normality is assumed in parametric statistical tests such as t-test or ANOVA. Normal distributed populations are those presenting classical bell-shape curves to illustrate their probability density function. The frequency distribution of a normal population is a symmetric histogram with most of the frequency counts bunched in the middle and equally likely positive and negative deviations from this central value. The frequencies of these deviations fall off quickly as we move further away from this central point corresponding to the mean. Data sampled from normal populations can be fully characterized by just two parameters: the mean (m) and the standard deviation (σ). Normality assumption can be evaluated either statistically or graphically. We propose two tests to statistically evaluate normality: Shapiro-Wilk and Kolmogorov-Smirnov, the former better behaved in the case of small samples sizes (
i.e., N < 50) [
27]. It is worth recalling that the term normal just applies to the entire population and not to the sample data. Hence, none of these tests would answer whether our dataset is normal or not. Their derived p-values must be interpreted as the probability of the data to be sampled from a normal distribution. On the other hand, testing normality is a matter of paradox: for small samples sizes normality tests lack from power to detect non-normal distributions and as sample size increases normality becomes less troublesome thanks to the Central Limit Theorem. Since parametric tests are robust again mild violations of normality (and equality of variances as well), the practice of preliminary testing these two assumptions has been regarded as setting out in a rowing boat in order to test whether it is safe to launch an ocean liner [
29]. Additionally, normality tests can be complemented with descriptive statistics such as Skewness and Kurtosis. On the other hand, graphical methods such as histograms, probability plots or Q-Q plots might result also helpful as tools to evaluate normality. Their use, however, is rather limited at exploratory stage of LC-MS untargeted metabolomic data since it is unfeasible to examine each one of these plots for each mzRT feature detected.
Another of the assumptions of a parametric test is that the within-group variances of the groups are all the same (exhibit homoscedasticity or homogeneity of variances). If the variances are different from each other (exhibit heteroscedasticity), the probability of obtaining a "significant" result even though the null hypothesis is true may be greater than the desired alpha level. There are both graphical and statistical methods for evaluating homoscedasticity. The graphical method is the so-called boxplot but again, its use is rather limited because the impossibility to evaluate each one of them separately. The statistical methods are Levene’s and Bartlett tests, the former the less sensitive to departures from normality. In both cases, the null hypothesis states that the group variances are equal. Resulting p-value < 0.05 indicate that the obtained differences in sample variances are unlikely to have occurred based on random sampling. Thus, the null hypothesis of equal variances is rejected and it is concluded that there is a difference between the population variances.
The third assumption refers to independence. Two events are independent when the occurrence of one event makes it neither more nor less probable that the other occurs. In our metabolomic context, the knowledge of the value of one sample entering the study provides no clue about the value of another sample to be drawn.
8. The Fold Change Criteria
A common practice to identify mzRT features of relevance within a dataset is to rank these features according their fold change (FC). FC can be though as the magnitude of difference between the two populations under study. For each mzRT feature, a FC value is computed according to equation 5 in which X represents the average raw intensities across “case” group and Y represents the average raw intensities across “control” group. Whenever the raw intensities of the “control” group are larger than in the “case” group, this ratio should be inverted and sign should be conveniently changed to indicate a decrease of the case group relative to the control. Of mention, in paired-data designs, fold change should be calculated as the average of each individual fold change across all sample pairs.
In formal statistical terms, a mzRT feature is claim to be varied among two conditions when its relative intensity values change systematically between these two condition regardless on how small this change is. However, significance does not contain information about the magnitude of this change. For a metabolomics standpoint, a metabolic feature is considered to be relevant only when this change result in a worthwhile amount. Hence, significantly varied mZRT are ranked according to their FC value. Subsequent MS/MS chemical structural identification experiments are performed on those metabolic features resulting above a minimum FC cutoff value. It has been demonstrated that a 2-FC cutoff for metabolomics studies using human plasma or CSF minimizes the effects of biological variation inherent in a healthy control group [
26]. However, this cutoff value is set rather arbitrarily and based on similar FC cutoff values routinely applied in gene chip experiments.
9. Univariate LC-MS Untargeted Analysis Workflow
The typical univariate data analysis flow diagram for untargeted LC-MS metabolomics experiments is summarized in
Figure 5. The ultimate goal is to constraint the number of initially detected mzRT features to an amenable number for further MS/MS identification experiments. Only those mZRT features showing both statistically significant changes with delimited chance for false positives in their relative intensity and a minimum FC are going to be retained. Steps 1-5 are below summarized:
STEP1: Use quality control check to get rid-out of those mZRT features that do not contain biological information. Ideally QC samples should be measured. Then, compute CVQC and proceed to retain only those metabolic features presenting CVQC < 20%. If QC samples are not available, an alternative procedure is to compute CVT and retain those mZRT with CVT > 20%.
STEP2: Mind the experimental design to select the best suited statistical test to apply. Check whether your data is paired or not, i.e., whether your groups are related such as in our example#3 (individuals prior to treatment are uniquely matched to the same individual after the treatment). Afterwards, check normality and equality of variances assumptions. Be aware that performances of the normality tests might be hampered by low samples sizes dataset commonly found in LC-MS untargeted metabolomics studies. Despite this, working on such tests might be useful to gain some insights in to the data distribution.
STEP 3: Compare mean or medians of your dataset performing statistical inference and trying to apply statistical tests thoughtfully instead of mechanically. Try to be aware of the tests weaknesses when applying it. Once we have taken the decision on whether using parametric or non-parametric tests, it is important to stick on the same approach through the rest of the data analysis procedure. This is to plot our results in the form of medians instead of means whenever we choose to use a non-parametric statistical test.
STEP4: Account for multiple testing. Report the number of positive false findings after FDR correction. Plot histograms of p-values frequency distribution to get an overview of whether a dataset contains significant differences. Decide a FDR threshold to accept. A general consensus is to accept 5% of FDR level but there is nothing special about this value and each researcher might justify their assumed FDR value, which should be fixed before data is collected.
Figure 5.
General flow chart for univariate data analysis of untargeted LC-MS-based metabolomics data. Different colors for the four working examples indicate the initial number and the retained number of mzRT features in each step. FDR and FC value are fixed at 5% level 1.5-cutoff values respectively.
STEP5: Compute mean or median FC depending on the test used to perform statistical inference. Fix a cutoff FC value. From our in-house experience we recommend an arbitrary 1.5-FC cutoff value meaning a minimum of 50% of variation in the two groups compared. Rank your significant list of features according the FC value. Retain those significant features with higher FC values for MS/MS experiments and follow-up validation studies.
Following steps 1-5 described above, those metabolites identified using MS/MS experiments for example #2 are summarized in
Table 4. Of mention all metabolites identified meet the statistical criteria described above regardless of using either parametric or non-parametric tests. Notice the small number of properly identified metabolites as compared to the high number of features surviving statistical criteria. It is important to mention that in the best optimistic case the number of metabolite identifications showing MS/MS confirmation use to be in the tens after a formal untargeted metabolomics experiment. Conversely, in case of putative identifications based on exact masses, the number of metabolites reported is much higher. However, recall that such metabolites are just putatively identified. Considering that replication experiments are necessary to undeniably ascertain the role of the metabolites found to be relevant in the untargeted study, a strict identification of the metabolites is essential. In this sense, our work-flow data analysis represents the first step for a successful identification of those metabolites.
Table 4.
Statistics summary of those metabolites identified using MS/MS experiments in working example #2. Unpaired t-test and Mann-Whitney test were used for parametric and non-parametric hypoxic and normoxic retinas comparison respectively. Correction for multiple testing was performed assuming 5% FDR.
| | Parametric Test | Non-parametric |
|---|
| | p-value | q- value | FC (mean) | p-value | q-value | FC (median) |
|---|
| Hexadecenoylcarnitine | 3.31×10-13 | 1.05×10-10 | 5.0 | 2.49×10-05 | 3.18×10-04 | 4.9 |
| Acetylcarnitine-derivative | 1.10×10-13 | 5.02×10-11 | 7.2 | 2.49×10-05 | 3.18×10-04 | 7.5 |
| Tetradecenoylcarnitine | 1.29×10-13 | 5.29×10-11 | 8.8 | 2.49×10-05 | 3.18×10-04 | 8.8 |
| Decanoylcarnitine | 7.79×10-11 | 1.03×10-08 | 5.7 | 2.49×10-05 | 3.18×10-04 | 5.6 |
| Laurylcarnitine | 8.48×10-11 | 1.06×10-08 | 9.2 | 2.49×10-05 | 3.18×10-04 | 8.7 |
| 7-ketocholesterol | 4.00×10-09 | 1.92×10-07 | 3.1 | 2.49×10-05 | 3.18×10-04 | 3.3 |
| 5,6β-epoxy-cholesterol | 2.12×10-08 | 6.61×10-07 | 5.1 | 2.49×10-05 | 3.18×10-04 | 7.0 |
| 7α-hydroxycholesterol | 3.88×10-08 | 1.07×10-06 | 4.1 | 2.49×10-05 | 3.18×10-04 | 4.5 |
| All-trans-Retinal | 1.26×10-05 | 9.24×10-05 | -3.0 | 4.01×10-05 | 3.98×10-04 | -2.8 |
| Octanoylcarnitine | 9.21×10-05 | 4.28×10-04 | 5.5 | 5.09×10-03 | 1.14×10-02 | 17.2 |