1. Introduction
In the last two years, we have witnessed extraordinary developments on experimental tests of inflationary models [
1], based on studies of photons in the Cosmic Microwave Background radiation. In particular, the results of Planck collaboration [
2,
3,
4] and the associated non-observation of B-mode polarizations of primordial light fluctuations have imposed very stringent restrictions on single scalar-field models of slow-roll inflation, allowing basically models with a very low tensor-to-scalar fluctuation ratio
, with a scalar spectral index
and no appreciable running. In fact, the upper bound set by Planck collaboration [
2,
3,
4] on this ratio, as a consequence of the non-observation of B-modes, is
, but their favoured regions point towards
. This is a feature that characterizes the so-called Starobinsky-type (or
-inflation, with
R denoting the scalar spacetime curvature) inflationary models [
5]. The estimated energy scale
of inflation, which in inflaton-type models is related to the, approximately constant, scalar potential during inflation through
, reads [
1]:
where
is the reduced Planck mass (
G being the Newtonian constant). The upper bound
placed by the Planck collaboration implies:
The above can be rephrased as , where GeV is the Planck mass in natural units. This result is consistent with the well-known CMB bound on the temperature fluctuations induced by the tensor modes. As we will see, the actual value of H during inflation for the class of models under study satisfies , and hence, the CMB bound is preserved by them.
The recent joint BICEP2-Planck analysis [
6] confirmed the early Planck result, namely the likelihood curve for
r yields an upper limit
at
. Moreover, the present BICEP2-Planck data are consistent with a scalar spectral index
and no appreciable running, in agreement with the previous Planck data [
2,
3,
4]. Using the aforementioned new upper limit
, the Hubble parameter during slow-roll inflation
is estimated to be below:
and hence,
. Because of the low significance of the new limit on
r, the possibility that
r is actually much smaller than the current upper limit
remains as natural as it was before. In fact, nothing actually prevents at present that the typical value of the tensor to scalar ratio can be, for example,
, and in this sense, the Starobinsky-type scenarios can still be considered as a serious possibility to describe the inflationary Universe. Following this point of view, we continue in this paper with the investigation of Starobinsky-like models as potential candidates for the realistic implementation of inflation compatible with the data.
In previous publications one of us (Nick E. Mavromatos) with collaborators [
7,
8] discussed the dynamical breaking of supergravity (SUGRA) theories via gravitino condensation and demonstrated [
9] the compatibility of this scenario with Starobinsky-like [
5] inflationary scenarios. As we discussed, this phase is characterized by the dynamical emergence of a de Sitter background. As argued in [
7,
8], the Starobinsky-type inflation appears much more natural (from the point of view of the order of the parameters involved) than a hill-top inflation scenario [
10] in which the gravitino condensate itself is the inflaton field. In the latter, very large values of the wave function re-normalization of the condensate field are required to ensure slow-roll inflation if one insists on (phenomenologically realistic) sub-Planckian supersymmetry breaking scales. It is important to notice at this point that in the original Starobinsky model [
5], the
terms crucial for inflation arise from the conformal anomaly in the path integral of massless (conformal) matter in a de Sitter background, and thus, their coefficient is arbitrary and can only be fixed phenomenologically. A similar, although not identical, situation occurs in the context of anomaly-induced inflation [
11,
12,
13], where the term
is absent at the classical level, but is generated from the conformal anomaly. In this case, however, the coefficient of
(entering the
β-functions and controlling the stability of inflation) presents also some arbitrariness, which can only be fixed by a special re-normalization condition. Par contrast, in the considered SUGRA scenario, such terms arise in the one-loop effective action of the gravitino condensate field, evaluated in a de Sitter background, after integrating out massive gravitino fields, whose mass was generated dynamically. The order of the de Sitter cosmological constant,
, that breaks supersymmetry and the gravitino mass are all evaluated dynamically (self-consistently) in our approach from the minimization of the effective potential. Thus, the resulting
coefficient, which determines the phenomenology of the inflationary phase, is calculable [
9].
Also very important for our considerations is the framework of the running vacuum model (RVM) [
13,
14,
15,
16,
17,
18,
19]; see [
20,
21,
22] and the references therein for a recent detailed exposition. The implications of these dynamical vacuum models have recently been analysed both for the early Universe [
22,
23,
24,
25,
26,
27,
28], as well as for the phenomenology of the current Universe [
29,
30,
31]; see also [
32,
33,
34,
35,
36,
37,
38,
39,
40] for previous analyses.
In regard to the early Universe, we emphasize that the RVM defines a class of non-singular inflationary scenarios with graceful exit into the standard radiation regime. These models are related to Starobinsky inflation models, although they are not equivalent. We will discuss in this paper the correspondence between them and most particularly with the dynamically-broken SUGRA model with gravitino condensation that we have mentioned above. It is especially remarkable that such a specific implementation of the SUGRA model leads, as we will show in this paper, to the effective behaviour of the RVM with calculable coefficients. In this way, the former automatically benefits from the successful consequences of the latter. Let us mention that the RVM also provides some important clues for alleviating the cosmological constant problem [
20,
21].
Finally, we would like to mention that the RVMs have been tested against the wealth of accurate SNIa + BAO +
+ LSS + BBN + CMB data (see [
41] for a recent summary review), and they turn out to provide a quality fit that is significantly better than the ΛCDM. This fact has become especially prominent in light of the most recent works [
42,
43]. Therefore, there is every motivation for further investigating these dynamical vacuum models from different perspectives, with the hope of finding possible connections with fundamental aspects of the cosmic evolution. In point of fact, this is the main aim of this work.
The structure of the article is as follows. The general framework of the RVM is introduced in
Section 2. The basic theoretical elements of the Starobinsky inflation are presented in
Section 3. The main properties of the dynamical breaking of local SUGRA theory and its connection to Starobinsky-type inflation are reviewed in
Section 4. In
Section 5, we demonstrate how the RVM describes the effective framework of the Starobinsky [
5] and the dynamically-broken SUGRA [
10] models at the inflationary epoch. Finally, our conclusions are summarized in
Section 6.
3. Generic Starobinsky Inflation
Starobinsky inflation is the oldest model of inflation [
5], prior to the traditional, scalar-field-based, inflaton models. It is characterized for being able to realize the de Sitter (inflationary) phase from the gravitational field equations derived from a four-dimensional action that includes higher curvature terms, specifically of the type involving the quadratic curvature correction
[
5]:
Our metric signature is
, and the definitions of the Ricci and Riemann curvature tensors are
and
, respectively, i.e., we follow the exact three-sign conventions
of Misner–Thorn–Wheeler [
47]).
In the above equation,
(in the units of
we are working on),
is Newton’s (gravitational) constant in four spacetime dimensions, with
the Planck mass, and
is a constant of mass dimension one, characteristic of the model. Notice that the curvature terms in the action are just the dimension-four combination
. With this normalization,
gives the value of the so-called scalaron mass. The smaller is
in Planck mass units (i.e., the larger is the dimensionless parameter
in front of
), the longer is the inflationary time (cf. Figure 2 of [
22]). Of course,
cannot be much below the natural scale of inflation, and in fact, it should be of the same order, i.e.,
, where
is some GUT scale below the Planck mass. Typically,
.
The most relevant feature of this model is that inflationary dynamics is driven by the purely gravitational sector, through the
terms. From a microscopic point of view, these terms can be viewed as the result of quantum fluctuations (at one-loop level) of conformal (massless or high energy) matter fields of various spins, which have been integrated out in the relevant path integral in a curved background spacetime [
48,
49,
50]. The model in fact is to be understood in the context of QFT in curved spacetime. The quantum mechanics of this model, by means of tunnelling of the Universe from a state of “nothing” to the inflationary phase of [
5], has been discussed in detail in [
51]. The above considerations necessitate truncation to one-loop quantum order and to curvature-square (four-derivative) terms, which implies that there must be a region of validity for curvature invariants, such that
. Recalling that
in the inflationary phase (where
is the nearly constant Hubble rate in that phase), we observe that this is indeed a condition satisfied in phenomenologically-realistic scenarios of inflation [
1,
2], for which the inflationary Hubble scale
is typically constrained to obey (
2) (Planck data [
2,
3,
4]) or (
3) (BICEP2 data), which are at present essentially the same.
Although the inflation in this model is not driven by fundamental rolling scalar fields, nevertheless, the model (
5) (and for that matter, any other model where the Einstein–Hilbert spacetime Lagrangian density is replaced by an arbitrary function
of the scalar curvature) is conformally equivalent to that of an ordinary Einstein-gravity coupled to a scalar field with a potential that drives inflation [
52,
53]. To see this, one firstly linearises the
terms in (
5) by means of an auxiliary (Lagrange-multiplier) field
, before rescaling the metric by a conformal transformation and redefining the scalar field (so that the final theory acquires canonically-normalised Einstein and scalar-field terms):
where again,
. These steps may be understood schematically via:
where the arrows have the meaning that the corresponding actions appear in the appropriate path integrals. The ensuing effective potential
is given by:
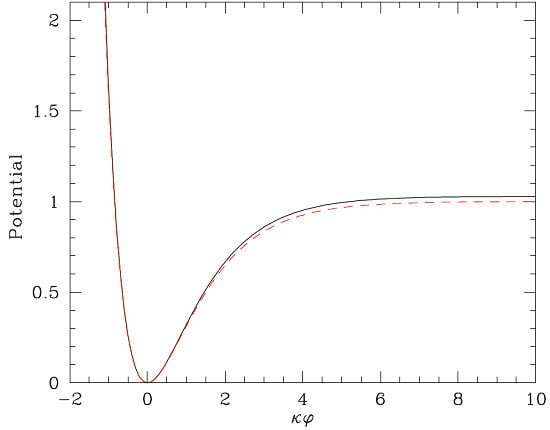
One can check that the mass of the scalaron, which can be seen as the new gravitational degree of freedom that the conformal transformation was able to elucidate from the Starobinsky action, is indeed given by the parameter
:
Note that for
, one has
, and the two conformally equivalent metrics coincide at this point. The effective potential for the scalar d.o.f. that conformally replaces the effect of the
term is plotted in
Figure 1.
We observe that
is sufficiently flat for
(i.e., for sufficiently large values of
ϕ as compared to the reduced Planck scale) to produce phenomenologically-acceptable inflation. Obviously, the scalaron field
ϕ is effectively playing the role of the inflaton in this context. The difference with the usual inflaton is that
ϕ is not a new scalar d.o.f. imported from outside the gravitational action, but just an integral part of it, namely it is just a gravitational d.o.f. that describes in an effective (and very convenient) way the
term of (
5). The Starobinsky model based on the action (
5) indeed fits excellently with the Planck data on inflation [
2,
3,
4] and, also, the corresponding data from the joint BICEP2-Planck analysis [
6].
Quantum-gravity corrections in the original Starobinsky model (
5) have been considered recently in [
54] from the point of view of an exact re-normalisation-group analysis [
55,
56]. It was shown that the non-perturbative beta-functions for the ‘running’ of Newton’s ‘constant’ G and the dimensionless inverse
coupling
in (
5) imply an asymptotically-safe ultraviolet (UV) fixed point for the former (that is, G(
) → constant, for some four-momentum cut-off scale
k), in the spirit of Weinberg [
57], and an attractive asymptotically-free (
) point for the latter. In this sense, the smallness of the (inverse)
coupling, required for agreement with inflationary observables [
2,
3,
4], is naturally ensured by the presence of the asymptotically-free UV fixed point.
The agreement of the model of [
5] with the Planck data triggered an enormous interest in the current literature, and indeed, Starobinsky inflation has been revisited from various points of view, such as its connection with no-scale supergravity [
58,
59] and (super)conformal versions of supergravity and related areas [
60,
61,
62,
63,
64,
65,
66,
67]. In the latter works, however, the Starobinsky scalaron field is fundamental, arising from the appropriate scalar component of some chiral superfield that appears in the superpotentials of the model.
Although of great value, illuminating a strong connection between supergravity models and inflationary physics, and especially for explaining the low-scale of inflation compared to the Planck scale, these works contradict the original spirit of the Starobinsky model (
5), where, as mentioned previously, the higher curvature corrections are viewed as arising from quantum fluctuations of matter fields in a curved spacetime background, such that inflation is driven by the pure gravity sector in the absence of fundamental scalars. On the other hand, the scenario of [
9], in which a Starobinsky-type inflation arises in the massive gravitino phase of SUGRA models, after integrating out the massive degrees of freedom, is in the same spirit of Starobinsky and, even better, in the sense that the model does not have to assume the dominance of conformal matter during inflation.
We next proceed to summarize the construction of the one-loop effective action of the massless degrees of freedom after massive gravitino integration in this dynamically-broken SUGRA model with spontaneous breaking of global supersymmetry (SUSY) [
7,
8].
4. Starobinsky-Type Inflation in Dynamically-Broken SUGRA
Dynamical breaking of SUGRA, in the sense of the generation of a mass for the gravitino field , whilst the gravitons remain massless, occurs in the model as a result of the four-gravitino interactions characterizing the SUGRA action, arising from the torsionful contributions of the spin connection, characteristic of local supersymmetric theories.
Our starting point is the
(on-shell) action for ‘minimal’ Poincaré supergravity in the second order formalism [
68,
69]:
where
and
are defined via the torsion-free connection; and given the gauge condition
,
arising from the fermionic torsion parts of the spin connection. Extending the action off-shell requires the addition of auxiliary fields to balance the graviton and gravitino degrees of freedom. These fields however are non-propagating and may only contribute through the development of scalar vacuum expectation values, which would ultimately be re-summed into the cosmological constant.
Making further use of the above gauge condition together with the Fierz identities (as detailed in [
7,
8]), we may write:
where the couplings
,
and
express the freedom we have to rewrite each quadrilinear in terms of the others via Fierz transformation. This freedom in turn leads to a known ambiguity in the context of (perturbative) mean field theory [
70] and can only be resolved by a non-perturbative treatment.
Specifically, we wish to linearise these four-fermion interactions via suitable auxiliary fields, e.g.,
where the equivalence (at the level of the action) follows as a consequence of the subsequent Euler–Lagrange equation for the auxiliary scalar
σ. Our task is then to look for a non-zero vacuum expectation value
, which would induce as an effective mass
for the gravitino. This is however complicated by the fact that our coupling
into this particular channel is, by virtue of Fierz transformations, ambiguous at a perturbative level, and as mentioned, in order to fix them, a fully non-perturbative treatment of SUGRA-like models would be required, which are not currently at hand. Nevertheless, there is another way out [
7,
8,
10], whereby the Fierz ambiguities may be absorbed by dilaton-expectation-value shifts in an extension of
SUGRA, which incorporates local supersymmetry in the Jordan frame, enabled by an associated dilaton superfield [
71,
72]. The (logarithm of the) scalar component
ϕ of the latter can be either a fundamental spacetime scalar mode of the gravitational multiplet, i.e., the trace of the graviton (as happens, for instance, in supergravity models that appear in the low-energy limit of string theories) or a composite scalar field constructed out of matter multiplets. In the latter case, these could include the standard model fields and their superpartners that characterise the next-to-minimal supersymmetric standard model [
73], which can be consistently incorporated in such Jordan frame extensions of SUGRA.
Upon appropriate breaking of conformal symmetry, induced by specific dilaton potentials (which we do not discuss here), one may then assume that the dilaton field acquires a non-trivial vacuum expectation value
, thus absorbing any ambiguities in the value of the appropriate coefficient
induced by Fierz (
12). One consequence of this is then that in the broken conformal symmetry phase, the resulting supergravity sector, upon passing (via appropriate field redefinitions) to the Einstein frame, is described by an action of the form (
10), but with the coupling of the gravitino four-fermion interaction terms being replaced by:
while the Einstein term in the action carries the standard gravitational coupling
. For phenomenological reasons, associated with gravitino masses in the ball-park of GUT scales, one must have
. This is assumed to be guaranteed by appropriate microscopic dilaton potentials that break the (super)conformal symmetry of the Jordan-frame SUGRA appropriately.
To induce the super-Higgs effect [
74], we couple to the action (
10) the Goldstino associated to global supersymmetry breaking via the addition of:
where
λ is the Goldstino,
expresses the scale of global supersymmetry breaking and ... represents higher order terms, which may be neglected in our weak-field expansion of the determinant. It is worth emphasising at this point the universality of (
15); any model containing a Goldstino may be related to
via a non-linear transformation [
75], and thus, the generality of our approach is preserved.
Upon the aforementioned gauge choice for the gravitino field
and an appropriate redefinition, one may eliminate any presence of the Goldstino field from the final effective action describing the dynamical breaking of local supersymmetry, except the cosmological constant term
in (
15), which serves as a reminder of the pertinent scale of supersymmetry breaking. The non-trivial energy scale this introduces, along with the disappearance (through field redefinitions) of the Goldstino field from the physical spectrum and the concomitant development of a gravitino mass, characterises the super-Higgs effect.
The linearisation of the four-gravitino terms (
13), when combined with the
term of the super-Higgs effect, implies a tree-level cosmological constant:
which must be negative due to the incompatibility of supergravity with de Sitter vacua (notice that in our conventions, both σ and f have dimension in natural units).
The one-loop effective potential for the scalar gravitino condensate field
(with vacuum expectation value
) has a double-well shape as a function of
, which is symmetric about the origin (cf.
Figure 2), as dictated by the fact that the sign of a fermion mass does not have physical significance. Dynamical generation of the gravitino mass occurs at the non-trivial minima corresponding to
. The potential of the
field is also flat near the origin, and this has been identified in [
10] with a first inflationary phase.
In [
7,
8], the one-loop effective potential was derived by first formulating the theory on a curved de Sitter background [
76,
77], with cosmological constant (one-loop induced)
, not to be confused with the (negative) tree-level one
(
16), and then integrating out spin-two (graviton) and spin 3/2 (gravitino) quantum fluctuations in a given class of gauges (physical), before considering the flat limit
in a self-consistent way. The detailed analysis in [
7,
8], performed in the physical gauge, has demonstrated that the dynamically-broken phase is then stable (in the sense of the effective action not being characterized by imaginary parts) provided the scale of the gravitino condensate is equal to or below the scale of spontaneous breaking of global SUSY:
which guarantees the aforementioned result on the necessity of the negative nature of the tree-level cosmological constant (
16).
The former result demonstrates the importance of the existence of the global SUSY breaking scale for the stability of the phase where dynamical generation of gravitino masses occurs, which was not considered in the previous literature [
78,
79]. In super-conformal versions of SUGRA, e.g., those in [
71,
72,
73], phenomenologically realistic scales for
and gravitino mass of order of the GUT scale appear for appropriate values of the expectation value of the conformal factor. These imply inflationary scenarios in perfect agreement with the Planck data [
2,
3,
4,
10], on equal footing with the original Starobinsky model.
In [
9], we considered an extension of the analysis of [
7,
8] to the case where the de Sitter parameter Λ is perturbatively small compared to
, but non-zero, so that truncation of the series to order
suffices. This is in the spirit of the original Starobinsky model [
5], with the role of matter fulfilled by the now-massive gravitino field. Specifically, we were interested in the behaviour of the effective potential near the non-trivial minimum, where
is a non-zero constant (cf.
Figure 2). The one-loop effective potential, obtained by integrating out [
76,
77] gravitons and (massive) gravitino fields in the scalar channel (after appropriate Euclideanisation), may be expressed as a power series in Λ:
where
denotes the classical action with tree-level cosmological constant
(to be contrasted with the one-loop cosmological constant Λ):
with
denoting the fixed
background; we expand around (
, and the four-dimensional Euclidean volume is
); the
α’s indicate the bosonic (graviton) and fermionic (gravitino) quantum corrections at each order in Λ. The reader should notice that, upon the restriction (
17) guaranteeing the absence of imaginary parts in the one-loop effective action, the tree-level cosmological constant (
16)
, while the one-loop one
, as appropriate for a de Sitter background. Thus,
should not be confused with the current-epoch positive cosmological constant
, which we introduce later on, in
Section 5.2, when we discuss the running vacuum model (RVM) (cf. (
57)).
The leading order term in Λ is then the effective action found in [
7,
8] in the limit
,
with:
where:
and:
indicate the leading (as
) contributions to the effective potential from bosonic (graviton) and fermionic (gravitino) quantum fluctuations, respectively, to one-loop order. Above,
μ is an RG scale, associated with a short-distance proper time cut-off [
7,
8], not to be confused with the RG scale of the RVM
(cf.
Section 2), which is such that the flow from ultraviolet (UV) to infrared (IR) corresponds to the direction of increasing
μ;
denotes the gravitino scalar condensate
at the non-trivial minimum of the one-loop effective potential (cf.
Figure 2);
is the conformally-rescaled gravitational constant in the Jordan-frame SUGRA model of [
71,
72], defined in (
14), corresponding to a non-trivial v.e.v.of the conformal (‘dilaton’) factor,
, assumed to be stabilized by means of an appropriate potential, leading to the breaking of the conformal symmetry. In the case of standard
SUGRA,
.
The remaining (higher order in Λ) one-loop quantum corrections then, proportional to Λ and
may be identified respectively with Einstein–Hilbert
R-type and Starobinsky
-type terms in an effective action of the form
where we have combined terms of order
into curvature scalar square terms. The reader should recall at this stage that the sign of
g in
and the overall minus sign in front of the right-hand-side of (
24) is due to the Euclidean-signature formulation of the path integral and disappears upon analytic continuation back to the Minkowski spacetime at the end of the computations, which is necessary in order to make contact with phenomenology/cosmology (see, e.g., (
5)). This should be understood in what follows, and especially in the context of linking the SUGRA model with the RVM in
Section 5.
For general backgrounds, such terms would correspond to invariants of the form
,
and
, which for a de Sitter background all combine to yield
terms. In the pure SUGRA case, with no dilaton frame functions, the fact that the Gauss–Bonnet combination
is a total derivative in four spacetime dimension implies that one can consider only the Ricci-scalar and Ricci-tensor squared terms as independent. This is not the case though in the conformal SUGRA case [
71,
72].
The coefficients
and
in (
24) absorb the non-polynomial (logarithmic) in Λ contributions, so that we may then identify (
24) with (
18) via:
where we note that
is dimensionless, whereas
has the dimension of inverse mass squared. The coefficients
,
in Equation (
25) can be computed using the results of [
7,
8], derived via an asymptotic expansion:
and:
To identify the conditions for phenomenologically-acceptable Starobinsky inflation around the non-trivial minima of the broken SUGRA phase of our model, we impose first the cancellation of the “classical” Einstein–Hilbert space term
by the “cosmological constant” term
, i.e., that:
This condition should be understood as a necessary one characterizing our background in order to produce phenomenologically-acceptable Starobinsky inflation in the broken SUGRA phase following the first inflationary stage, as discussed in [
10]. This may naturally be understood as a generalization of the relation
, imposed in [
7,
8] as a self-consistency condition for the dynamical generation of a gravitino mass in the flat (zero Λ) limit.
From Equation (
28), it follows that the (positive) cosmological constant
satisfies the four-dimensional Einstein equations in the non-trivial minimum and, in fact, coincides with the value of the one-loop effective potential of the gravitino condensate at this minimum. As we discussed in [
7,
8], this non-vanishing positive value of the effective potential is consistent with the generic features of dynamical breaking of supersymmetry [
80]. In terms of the Starobinsky inflationary potential (
8), the value
corresponds to the approximately constant value of this potential in the high
ϕ-field regime (
) of
Figure 1, in the flat region where Starobinsky-type inflation takes place. Thus, we may set:
where
is the (approximately) constant Hubble scale during inflation, which is constrained by the current data to satisfy (
2) or (
3). In the SUGRA context under discussion,
is linked to the scale of global SUSY breaking through
.
The effective Newton’s constant in (
24), after the imposition of (
28), is then defined as:
and from this, we can express the effective Starobinsky parameter (
5) in terms of
as:
This condition thus makes a direct link between the action (
18) with a Starobinsky type action (
5). Comparing to (
5), we can determine the effective scalaron mass in this case:
As we know, this mass parameter also sets the order of magnitude of the inflationary scale in the Starobinsky model.
We may then determine the coefficients
and
in order to evaluate the scale
of the effective Starobinsky potential given in
Figure 1 in this case and, thus, the scale of the second inflationary phase.
In [
9], we searched numerically for points in the parameter space, such that:
The effective equations
are satisfied, together with the condition (
28):
The cosmological constant Λ is small and positive, satisfying (
29), and for phenomenological reasons, it should be of order:
to ensure the validity of our expansion in Λ, consistent with the phenomenology of Planck-satellite data [
2,
3,
4].
The scalaron mass should also be of order
, hence allowing us to achieve phenomenologically-acceptable Starobinsky inflation in the massive gravitino phase, consistent with the Planck-satellite data [
2,
3,
4].
For
(i.e., for non-conformal supergravity), we were unable to find any solutions satisfying these constraints. This, of course, may not be surprising, given the previously demonstrated non-phenomenological suitability of this simple model [
7,
8]. If we consider
, however, we find that we are able to satisfy the above constraints for a range of values. A comment concerning SUGRA models in the Jordan frame with such large values for their frame functions is in order here. In our approach, the dilaton
could be a genuine (dimensionless) dilation scalar field arising in the gravitational multiplet of string theory, whose low-energy limit may be identified with some form of SUGRA action. In our normalization, the string coupling would be
. In such a case, a value of
would imply a large negative v.e.v. of the (four-dimensional) dilaton field of order
and, thus, a weak string coupling squared
, which may not be far from the values attained in realistic phenomenological string models. On the other hand, in the Jordan-frame SUGRA models of [
71,
72], the frame function reads
, in the notation of [
73] for the various matter super fields of the next-to-minimal supersymmetric standard model that can be embedded in such supergravities. The quantity
χ is a constant parameter. At energy scales much lower than GUT, it is expected that the various fields take on sub-Planckian values, in which case the frame function is almost one and, hence,
for such models today. To ensure
and, thus, large values of the frame function,
, as required in our analysis, one needs to invoke trans-Planckian values for some of the fields,
, and large values of
χ, which may indeed characterize the inflationary phase of such theories. A similar situation occurs for the values of the Higgs field (playing the role of the inflaton) in the non-supersymmetric Higgs inflation models [
81,
82]).
In general, typical values obtained in phenomenological-realistic conformal SUGRA models satisfy
(e.g., of order
, under the constraints (
29) and (
34), in such a way that:
Since the scale of SUSY breaking must be in the ballpark of the typical GUT scale associated with the inflation, namely
GeV
, from the above, we have
GeV
. As a result, the scale of the gravitino is some two to three orders of magnitude below the GUT scale, that is to say,
GeV
. These values are compatible with both the combined Planck and Bicep2 bound (
3) and the typical mass of the gravitino in this framework [
9].
Exit from the inflationary phase is, of course, a complicated issue, which we shall not discuss here at the level of the SUGRA model itself, aside from the observation that it can be achieved by coherent oscillations of the gravitino condensate field around its minima and subsequent decays to radiation and matter fields (thus requiring detailed knowledge of the matter content of the SUGRA models in order to arrive at quantitative predictions for the exit phase) or tunnelling processes à la Vilenkin [
51]. However, in the next section, we will show that the SUGRA model can be represented by an effective running vacuum model along the lines indicated in
Section 2, and from this point of view, the exiting from the inflationary phase into the standard radiation phase can be guaranteed on very general grounds.
Before doing so, though, we should make some important remarks concerning the presence of logarithms of the de Sitter scale Λ in the coefficients
of the curvature terms of the effective action (
24). When one computes the effective action in a fixed de Sitter background, it is tempting to identify a Λ term with the Ricci scalar, which eventually will be allowed to depend on time. Thus, naively, the presence of logarithms would imply non-polynomial terms of the form
, which would be problematic for any RVM interpretation of the exit from the inflationary phase, as it would contradict the spirit of the approach where only integer powers of the curvature terms would be allowed in the respective flow equations [
13,
14,
15,
17,
18,
19,
20,
21,
22]. Fortunately, this is not the case. To understand this, we first remark that any effective action obtained by integrating out massive degrees of freedom, such as gravitino fields, which we restrict ourselves here, must consist for reasons of covariance and consistency of the weak gravitational fluctuations about the de Sitter background only of polynomial structures of the curvature tensors, for instance to fourth order in derivatives terms involving the squares of the Ricci scalar and Ricci tensors and covariant derivatives thereof. Any
term would be incompatible with the weak gravity perturbative expansion about a background, say of constant non-zero curvature.
Thus, the coefficients
and
in the action (
24) are kept fixed, not undergoing temporal evolution, which is guaranteed by the fixing of the two free scales in the problem
μ (
35) and Λ (
29). Notice that the scale
μ should not be confused with the subsequent RG scale
that describes the cosmological evolution of the RVM vacuum (cf.
Section 2). Indeed, the scale
μ first of all is a high energy cut-off. As already mentioned, it plays the role of a proper-time cut-off scale [
7,
8], appearing in the integral representations of some
ζ-functions that are part of the determinants arising in the path integral of the SUGRA action arising from integrating out massive spin 3/2 (gravitino) and spin two (graviton) fluctuations about the de Sitter background. The scale
μ is therefore, in contrast to
, an inverse re-normalization group scale. Its value has to be fixed so as to guarantee SUGRA breaking and to generate a fixed gravitino mass, which should not depend on time. This implies that the spontaneous breaking of SUGRA and the inflationary phase are characterised by such fixed scales, which implies the time independence of Λ (or, equivalently, the Hubble parameter) during inflation, the gravitino mass, related to the gravitino condensate vacuum expectation value
and, thus, the coefficients
and
. On the other hand, integer positive powers of Λ appearing in the effective action may be replaced by higher order tensorial structures involving the square of the curvature tensors, which are allowed to vary with the cosmic time during the RVM phase after exiting from inflation. Notice that microscopically, the exit phase is characterised by an unknown sort of phase transition, either through decays of the gravitino condensates to matter parts and reheating of the inflated Universe, or tunnelling, as mentioned previously, and thus, using different RG running to relate various eras of the Universe after inflation is to be expected.