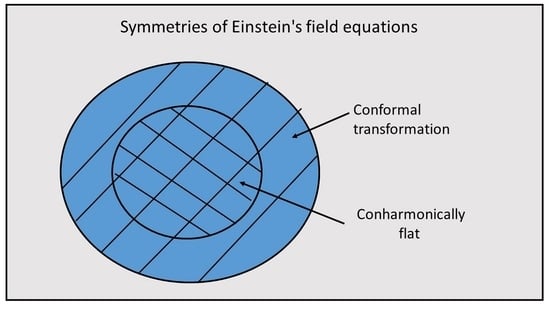
How Extra Symmetries Affect Solutions in General Relativity
Abstract
:1. Introduction
2. Conharmonic Curvature Tensor
3. Application to Cosmology
4. Additional Symmetry Requirement
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stephani, H.; Kramer, D.; MacCallum, M.; Hoenselaers, C.; Herlt, E. Exact Solutions of Einstein’s Field Equations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Schwarzschild, K. Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl. 1916, 7, 189–196. [Google Scholar]
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Weyl, H. Zur Gravitationstheorie. Ann. Phys. 1917, 54, 117–145. [Google Scholar] [CrossRef]
- Weyl, H. Zur allgemeinen Relativitatstheorie. Physikalische Zeitschrift 1923, 24, 230–232. [Google Scholar]
- Friedmann, A. On the Curvature of Space. Zeischrift fur Physik 1922, 10, 377–386. [Google Scholar] [CrossRef]
- Lemaitre, G. Un Univers homogene de masse constante et de rayon croissant rendant compte de la vitesse radiale des nebuleuses extra-galactiques. Annales de la Societe Scientifique de Bruxelles 1927, A47, 49–59. [Google Scholar]
- Robertson, H.P. On Relativistic Cosmology. Phil. Mag. 1928, 5, 835–848. [Google Scholar] [CrossRef]
- Walker, A.G. Relative coordinates. Proc. R. Soc. Edinb. 1932, 52, 345–353. [Google Scholar] [CrossRef]
- Einstein, A. Uber Gravitationswellen. In Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin); Deutsche Akademie der Wissenschaften zu Berlin: Berlin, Germany, 1918; pp. 154–167. [Google Scholar]
- Krasinski, A. Inhomogeneous Cosmological Models; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Stephani, H. Uber Losungen der Einsteinschen Feldgleichungen, die sich in einen funfdimensionalen flachen Raum einbetten lassen. Commun. Math. Phys. 1967, 4, 137–142. [Google Scholar] [CrossRef]
- Stephani, H. Some perfect fluid solutions of Einstein’s field equations without symmetries. Class. Quantum Grav. 1987, 4, 125–136. [Google Scholar] [CrossRef]
- Szekeres, P. A Class of Inhomogeneous Cosmological Models. Commun. Math. Phys. 1975, 41, 55–64. [Google Scholar] [CrossRef]
- Szekeres, P. Quasispherical gravitational collapse. Phys. Rev. D 1975, 12, 2941. [Google Scholar] [CrossRef]
- Barnes, A. On shear free normal flows of a perfect fluid. Gen. Relativ. Grav. 1973, 2, 105–129. [Google Scholar] [CrossRef]
- Ma, R.; Pei, D. Some curvature properties on Lorentzian generalized Sasakian-space-forms. Adv. Math. Phys. 2019, 2019, 5136758. [Google Scholar] [CrossRef]
- Shaikh, A.A.; Kundu, H.; Sen, J. Curvature properties of the Vaidya metric. Ind. J. Math. 2019, 61, 41–59. [Google Scholar]
- Tekin, P.; Atkan, N. eta-Einstein nearly Kenmotsu manifolds. Asian Eur. J. Math. 2019, 12, 2040010. [Google Scholar] [CrossRef]
- Tripathi, G.N.; Rastogi, R. On the conharmonic curvature tensor of a N(k)-contact metric manifold. RAOPS 2019, 18, 45–55. [Google Scholar]
- Baishya, K.K.; Eyasmin, S. Generalized weakly Ricci-symmetric (CS)(4)-spacetimes. J. Geom. Phys. 2018, 132, 415–422. [Google Scholar] [CrossRef]
- Bilen, L.; Gezer, A. On metric connections with torsion on the cotangent bundle with modified Riemannian extension. J. Geom. 2018, 109, 6. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Kishor, S. Some types of eta-Ricci solitons on Lorentzian para-sasakian manifolds. Facta Univ. Ser. Math. Inform. 2018, 33, 217–230. [Google Scholar]
- Prakasha, D.G.; Hadimani, B.S. On the conharmonic curvature tensor of Kenmotsu manifolds with generalized Tanaka-webster connection. Miskolc Math. Notes 2018, 19, 491–503. [Google Scholar] [CrossRef]
- Caliskan, N. On conharmonic curvature tensor of Sasakian structures on tangent bundles. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2018, 67, 282–290. [Google Scholar]
- Yildiz, A. f-Kenmotsu manifolds with the Schouten-Van Kampen connection. Publ. Inst. Math. 2017, 102, 93–105. [Google Scholar] [CrossRef]
- De, U.C.; Velimirovic, L.; Mallick, S. On a type of spacetime. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750003. [Google Scholar] [CrossRef]
- Vanli, A.T.; Unal, I. Conformal, concircular, quasi-conformal and conharmonic flatness on normal complex contact metric manifolds. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750067. [Google Scholar] [CrossRef]
- Yildirim, H. On the geometry of complex (kappa, mu)-spaces. Math. Nach. 2016, 289, 2312–2322. [Google Scholar] [CrossRef]
- Canuto, V.; Adams, P.J.; Hsieh, T.S.-H.; Tsiang, E. Scale-covariant theory of gravitation and astrophysical applications. Phys. Rev. D 1977, 16, 1643–1663. [Google Scholar] [CrossRef]
- Brans, C.H.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Ishii, Y. On conharmonic transfromations. Tensor 1957, 7, 73–80. [Google Scholar]
- Siddiqui, S.A. A Study of Curvature Tensors and Geometric Structures in General Relativity. Ph.D. Thesis, Aligarh Muslim University, Aligarh, India, 2009. [Google Scholar]
- Tiwari, R.K.; Singh, R. Role of conharmonic flatness in Friedmann cosmology. Astrophys. Space Sci. 2015, 357, 130. [Google Scholar] [CrossRef]
- Tiwari, R.K. Solution of conharmonic curvature tensor in General Relativity. J. Phys. Conf. Ser. 2016, 718, 032009. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.K.; Shrivastava, E. Conharmonically Flat Space with Variable Deceleration Parameter. Prespacetime J. 2017, 8, 808–817. [Google Scholar]
- Goyal, M.; Tiwari, R.K.; Pradhan, A. Decelerating to Accelerating FRW Universe with variable G and Λ in conharmonically flat space. New Astron. 2018, 66, 79. [Google Scholar] [CrossRef]
- Pradhan, A.; Dubey, V.C.; Sharma, U.K. A new class of holographic dark energy models in conharmonically flat space-time. New Astron. 2020, 77, 101360. [Google Scholar] [CrossRef]
- Kumar, R.; Srivastava, S.K. FRW-Cosmological Model for Conharmonically Flat Space Time. Int. J. Theor. Phys. 2013, 52, 589–596. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beesham, A.; Makhanya, F. How Extra Symmetries Affect Solutions in General Relativity. Universe 2020, 6, 170. https://doi.org/10.3390/universe6100170
Beesham A, Makhanya F. How Extra Symmetries Affect Solutions in General Relativity. Universe. 2020; 6(10):170. https://doi.org/10.3390/universe6100170
Chicago/Turabian StyleBeesham, Aroonkumar, and Fisokuhle Makhanya. 2020. "How Extra Symmetries Affect Solutions in General Relativity" Universe 6, no. 10: 170. https://doi.org/10.3390/universe6100170
APA StyleBeesham, A., & Makhanya, F. (2020). How Extra Symmetries Affect Solutions in General Relativity. Universe, 6(10), 170. https://doi.org/10.3390/universe6100170