Selecting Prices Determinants and Including Spatial Effects in Peer-to-Peer Accommodation
Abstract
:1. Introduction
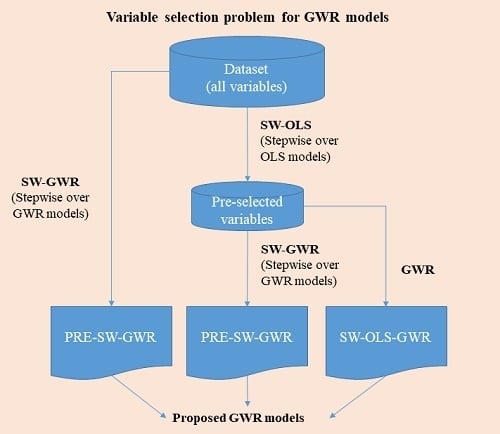
2. The Variable Selection in Geographic Weighted Regression (GWR) Models
3. Methods and Data
3.1. GWR Model
3.2. Model Selection Problem
3.3. Data Collection
4. Results and Discussion
4.1. SW-OLS-GWR Procedure
4.2. Pre-SW-GWR Procedure
4.3. SW-GWR Procedure
4.4. Comparing the Three Procedures
4.5. Results with GWR
5. Conclusions and New Working Lines
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Step | Variable | Description | Mean | sd | Min. | Max. |
| 1 | Bathrooms | Number of bathrooms | 1.289 | 0.644 | 0 | 6 |
| 2 | Pool | Pool existence (1: Yes; 0: No) | 0.357 | 0.479 | 0 | 1 |
| 3 | Person_cap | Maximum number of people who can be accommodated | 4.187 | 1.93 | 1 | 16 |
| 4 | #Properties | Number of properties managed by the host (1: Yes; 0: No) | 3.207 | 4.566 | 1 | 28 |
| 5 | Air_conditioning | Air conditioning availability (1: Yes; 0: No) | 0.274 | 0.446 | 0 | 1 |
| 6 | Beach200m | The beach is less than 200 m from the property (1: Yes; 0: No) | 0.169 | 0.375 | 0 | 1 |
| 7 | Cable_TV | Cable TV available (1: Yes; 0: No) | 0.278 | 0.448 | 0 | 1 |
| 8 | Reviews_count | Number of comments on the property | 15.059 | 18.476 | 0 | 181 |
| 9 | Dryer | Dryer available (1: Yes; 0: No) | 0.228 | 0.42 | 0 | 1 |
| 10 | Bedrooms | Number of bedrooms | 1.765 | 1.059 | 0 | 10 |
| 11 | Cancel_policy | Cancel policy: 3: Flexible; 4: Moderate; 5: Strict; 9: Super Strict | 4.317 | 0.79 | 3 | 9 |
| 12 | Dist_Airp | Distance to the airport | 23,873.19 | 9051.61 | 1809 | 42,751 |
| 13 | Hot_tub | Hot tub (1: Yes; 0: No) | 0.057 | 0.231 | 0 | 1 |
| 14 | Essentials | Essentials available (1: Yes; 0: No) | 0.942 | 0.233 | 0 | 1 |
| 15 | French | The host speaks French (1: Yes; 0: No) | 0.131 | 0.337 | 0 | 1 |
| 16 | Dishwasher | Dishwasher available (1: Yes; 0: No) | 0.086 | 0.28 | 0 | 1 |
| 17 | Cooking_basics | Cooking basics available (1: Yes; 0: No) | 0.255 | 0.436 | 0 | 1 |
| 18 | BBQ_grill | BBQ grill available (1: Yes; 0: No) | 0.058 | 0.234 | 0 | 1 |
| 19 | Pict_500m | Number of Flickr’s pictures at 500 m from the property | 1762.25 | 2262.92 | 0 | 8362 |
| 20 | Comp500 | Number of Airbnb’s properties at 500 m | 52.664 | 69.773 | 1 | 268 |
| 21 | German | The host speaks German (1: Yes; 0: No) | 0.165 | 0.371 | 0 | 1 |
| 22 | Beach500m | The beach is less than 500 m from the property (1: Yes; 0: No) | 0.336 | 0.472 | 0 | 1 |
| 23 | TV | TV available (1: Yes; 0: No) | 0.928 | 0.259 | 0 | 1 |
| 24 | Hair_dryer | Hair dryer available (1: Yes; 0: No) | 0.741 | 0.438 | 0 | 1 |
| 25 | Dist_LPGC | Distance to Las Palmas de Gran Canaria | 21,709.00 | 10,466.72 | 0 | 40,639 |
| 26 | Dist_Telde | Distance to Telde | 26,684.52 | 15,520.66 | 241.4 | 45,740.4 |
| 27 | Security_deposit | Security deposit | 79.224 | 173.493 | 0 | 5000 |
| 28 | Wireless_Internet | Wireless Internet available (1: Yes; 0: No) | 0.855 | 0.352 | 0 | 1 |
| 29 | Polish | The host speaks Polish (1: Yes; 0: No) | 0.012 | 0.111 | 0 | 1 |
| 30 | Elevator | Elevator existence (1: Yes; 0: No) | 0.357 | 0.479 | 0 | 1 |
| 31 | Family_kid_friendly | Family kids friendly (1: Yes; 0: No) | 0.792 | 0.406 | 0 | 1 |
| 32 | Exp_guest+Govid | Instant bookable allowed for experienced guests with government id (1: Yes; 0: No) | 0.067 | 0.25 | 0 | 1 |
| 33 | Is_superhost | The host is labelled as superhost (1: Yes; 0: No) | 0.231 | 0.422 | 0 | 1 |
| 34 | Extra_pillows | Extra pillows and blankets available (1: Yes; 0: No) | 0.181 | 0.385 | 0 | 1 |
| 35 | Refrigerator | Refrigerator available (1: Yes; 0: No) | 0.27 | 0.444 | 0 | 1 |
| 36 | Smoking_allowed | Smoking allowed (1: Yes; 0: No) | 0.294 | 0.456 | 0 | 1 |
| 37 | Free_parking | Free parking on premises (1: Yes; 0: No) | 0.444 | 0.497 | 0 | 1 |
| 38 | Cleaning_checkout | Cleaning before checkout available (1: Yes; 0: No) | 0.008 | 0.091 | 0 | 1 |
| 39 | Laptop_workspace | Laptop friendly workspace available (1: Yes; 0: No) | 0.511 | 0.5 | 0 | 1 |
| 40 | Bathtub_chair | Bathtub with shower chair (1: Yes; 0: No) | 0.003 | 0.056 | 0 | 1 |
| 41 | Kitchen | Availability of kitchen (1: Yes; 0: No) | 0.982 | 0.133 | 0 | 1 |
| 42 | Portuguese | The host speaks Portuguese (1: Yes; 0: No) | 0.03 | 0.17 | 0 | 1 |
| 43 | Bathtub | Bathtub existence (1: Yes; 0: No) | 0.051 | 0.22 | 0 | 1 |
| 44 | Oven | Oven available (1: Yes; 0: No) | 0.162 | 0.368 | 0 | 1 |
| 45 | Min_nights | Minimum number of nights to be rented | 3.698 | 1.901 | 1 | 21 |
| 46 | First_aid_kit | First aids kit existence (1: Yes; 0: No) | 0.403 | 0.491 | 0 | 1 |
| 47 | Safety_card | Safety card existence (1: Yes; 0: No) | 0.181 | 0.385 | 0 | 1 |
| 48 | Long_term_stays | Long term stays allowed (1: Yes; 0: No) | 0.154 | 0.361 | 0 | 1 |
| 49 | Hangers | Hangers availability (1: Yes; 0: No) | 0.853 | 0.354 | 0 | 1 |
| 50 | Identity_verified | The host’s identity is verified (1: Yes; 0: No) | 0.501 | 0.5 | 0 | 1 |
| 51 | Carbon_monoxide | Existence of carbon monoxide detector (1: Yes; 0: No) | 0.105 | 0.306 | 0 | 1 |
| 52 | Table_corner_guards | Table corner guards (1: Yes; 0: No) | 0.008 | 0.091 | 0 | 1 |
| 53 | Beachfront | Beachfront located (1: Yes; 0: No) | 0.064 | 0.244 | 0 | 1 |
| 54 | Wide_entryway | Wide entryway (1: Yes; 0: No) | 0.043 | 0.204 | 0 | 1 |
| 55 | Babysitter | Babysitter recommendations available (1: Yes; 0: No) | 0.033 | 0.179 | 0 | 1 |
| 56 | Crib | Crib available (1: Yes; 0: No) | 0.185 | 0.389 | 0 | 1 |
| 57 | Beds | Number of beds | 2.907 | 1.741 | 0 | 15 |
| 58 | Wheelchair_access | Wheelchair accessible (1: Yes; 0: No) | 0.121 | 0.326 | 0 | 1 |
| 59 | Stair_gates | Stair gates existence (1: Yes; 0: No) | 0.016 | 0.127 | 0 | 1 |
| 60 | Baby_monitor | Baby monitor available (1: Yes; 0: No) | 0.001 | 0.036 | 0 | 1 |
| 61 | Beach201_500 | The beach is between 201 and 500 m from the property (1: Yes; 0: No) | 0.166 | 0.372 | 0 | 1 |
| 62 | Spanish | The host speaks Spanish (1: Yes; 0: No) | 0.525 | 0.499 | 0 | 1 |
| 63 | English | The host speaks English (1: Yes; 0: No) | 0.554 | 0.497 | 0 | 1 |
| 64 | Not_Language | The host does not declare knowledge of any language (1: Yes; 0: No) | 0.404 | 0.491 | 0 | 1 |
| 65 | Wide_doorway | Wide doorway (1: Yes; 0: No) | 0.071 | 0.257 | 0 | 1 |
| 66 | Beach_essentials | Beach essentials available (1: Yes; 0: No) | 0.067 | 0.251 | 0 | 1 |
| 67 | High_chair | High chair available (1: Yes; 0: No) | 0.153 | 0.36 | 0 | 1 |
| 68 | Children’s_dinner | Children’s dinnerware available (1: Yes; 0: No) | 0.056 | 0.23 | 0 | 1 |
| 69 | Breakfast | Breakfast included (1: Yes; 0: No) | 0.04 | 0.196 | 0 | 1 |
| 70 | Stove | Stove available (1: Yes; 0: No) | 0.165 | 0.371 | 0 | 1 |
| 71 | Flat | It is a flat (1: Yes; 0: No) | 0.045 | 0.207 | 0 | 1 |
| 72 | Smooth_pathway | Existence of a smooth pathway to front door (1: Yes; 0: No) | 0.045 | 0.207 | 0 | 1 |
| 73 | Well_lit_path_to_entrance | Well lit path to entrance (1: Yes; 0: No) | 0.083 | 0.276 | 0 | 1 |
| 74 | Heating | Heating available (1: Yes; 0: No) | 0.243 | 0.429 | 0 | 1 |
| 75 | Danish | The host speaks Danish (1: Yes; 0: No) | 0.016 | 0.127 | 0 | 1 |
| 76 | Norwegian | The host speaks Norwegian (1: Yes; 0: No) | 0.021 | 0.144 | 0 | 1 |
| 77 | Garden | Garden or backyard existence (1: Yes; 0: No) | 0.082 | 0.274 | 0 | 1 |
| 78 | Self_Check_In | Self-Check In allowed (1: Yes; 0: No) | 0.073 | 0.259 | 0 | 1 |
| 79 | Private_entrance | Private entrance (1: Yes; 0: No) | 0.171 | 0.376 | 0 | 1 |
| 80 | Ground_floor_access | Ground floor access (1: Yes; 0: No) | 0.002 | 0.047 | 0 | 1 |
| 81 | Government_id | Instant bookable allowed for guests with government id (1: Yes; 0: No) | 0.098 | 0.297 | 0 | 1 |
| 82 | Shampoo | Shampoo available (1: Yes; 0: No) | 0.551 | 0.497 | 0 | 1 |
| 83 | Smart_lock | Access by mart lock (1: Yes; 0: No) | 0.003 | 0.056 | 0 | 1 |
| 84 | Washer | Washer available (1: Yes; 0: No) | 0.879 | 0.326 | 0 | 1 |
| 85 | Iron | Iron available (1: Yes; 0: No) | 0.713 | 0.453 | 0 | 1 |
| 86 | Indoor_fireplace | Indoor fireplace (1: Yes; 0: No) | 0.045 | 0.207 | 0 | 1 |
| 87 | Luggage_dropoff | Luggage drop-off allowed (1: Yes; 0: No) | 0.086 | 0.28 | 0 | 1 |
| 88 | Fixed_grab_bars | Fixed grab bars for shower toilet (1: Yes; 0: No) | 0.007 | 0.084 | 0 | 1 |
| 89 | Internet | Internet available (1: Yes; 0: No) | 0.366 | 0.482 | 0 | 1 |
| 90 | Pict_1km | Number of Flickr’s pictures at 1000 m from the property | 4606.07 | 5228.21 | 2 | 16,841 |
| 91 | Beach1000m | The beach is less than 1000 m from the property (1: Yes; 0: No) | 0.434 | 0.496 | 0 | 1 |
| 92 | Beach501_1000 | The beach is between 501 and 1000 m from the property (1: Yes; 0: No) | 0.098 | 0.298 | 0 | 1 |
| 93 | EV_charger | Electric vehicle charger (1: Yes; 0: No) | 0.001 | 0.03 | 0 | 1 |
| 94 | Wide_shower_toilet | Wide clearance to shower toilet (1: Yes; 0: No) | 0.024 | 0.154 | 0 | 1 |
| 95 | Dist_SBT | Distance to San Bartolomé de Tirajana | 22,967.50 | 17,514.79 | 147.2 | 47,735.7 |
| 96 | Wide_bed | Wide clearance to bed (1: Yes; 0: No) | 0.046 | 0.21 | 0 | 1 |
| 97 | Step_free_access | Step free access (1: Yes; 0: No) | 0.106 | 0.308 | 0 | 1 |
| 98 | Coffee_maker | Coffee maker available (1: Yes; 0: No) | 0.258 | 0.438 | 0 | 1 |
| 99 | Keypad | Access by keypad (1: Yes; 0: No) | 0.006 | 0.078 | 0 | 1 |
| 100 | Pocket_wifi | Pocket wifi available (1: Yes; 0: No) | 0.049 | 0.216 | 0 | 1 |
| 101 | Fire_extinguisher | Existence of fire extinguisher (1: Yes; 0: No) | 0.319 | 0.466 | 0 | 1 |
| 102 | Host_greets_you | Host greets you (1: Yes; 0: No) | 0.124 | 0.329 | 0 | 1 |
| 103 | Baby_bath | Baby bath available (1: Yes; 0: No) | 0.053 | 0.223 | 0 | 1 |
| 104 | Buzzer_wireless | Buzzer wireless intercom available (1: Yes; 0: No) | 0.257 | 0.437 | 0 | 1 |
| 105 | 24_hour_check_in | 24 h check in available (1: Yes; 0: No) | 0.23 | 0.421 | 0 | 1 |
| 106 | Wide_hallway | Wide hallway clearance (1: Yes; 0: No) | 0.056 | 0.23 | 0 | 1 |
| 107 | Lockbox | Lockbox existence (1: Yes; 0: No) | 0.035 | 0.184 | 0 | 1 |
| 108 | Children’s_books | Children’s books and toys available (1: Yes; 0: No) | 0.07 | 0.256 | 0 | 1 |
| 109 | Height_toilet | Accessible height toilet (1: Yes; 0: No) | 0.037 | 0.189 | 0 | 1 |
| 110 | Height_bed | Accessible height bed (1: Yes; 0: No) | 0.051 | 0.221 | 0 | 1 |
| 111 | Smoke_detector | Existence of smoke detector (1: Yes; 0: No) | 0.201 | 0.401 | 0 | 1 |
| 112 | Comp100 | Number of Airbnb’s properties at 100 m | 5.136 | 6.6 | 1 | 37 |
| 113 | Hot_water | Hot water available (1: Yes; 0: No) | 0.239 | 0.426 | 0 | 1 |
| 114 | Air_purifier | Air purifier available (1: Yes; 0: No) | 0 | 0.021 | 0 | 1 |
| 115 | Bed_linens | Bed linens available (1: Yes; 0: No) | 0.247 | 0.431 | 0 | 1 |
| 116 | Comp300 | Number of Airbnb’s properties at 300 m | 27.024 | 36.989 | 1 | 170 |
| 117 | Experienced | Instant bookable allowed for experienced guests (1: Yes; 0: No) | 0.032 | 0.176 | 0 | 1 |
| 118 | P&Play_travel_crib | Pack&Play travel crib available (1: Yes; 0: No) | 0.126 | 0.332 | 0 | 1 |
| 119 | has_profil | The host has profile (1: Yes; 0: No) | 0.997 | 0.056 | 0 | 1 |
| 120 | Handheld_shower | Handheld shower head existence (1: Yes; 0: No) | 0.033 | 0.179 | 0 | 1 |
| 121 | Pets_allowed | Pets allowed (1: Yes; 0: No) | 0.186 | 0.389 | 0 | 1 |
| 122 | Weekly_price | Discount factor for weekly rentals | 0.702 | 0.457 | 0 | 1 |
| 123 | Dist_beach | Distance, in meters, to the nearest beach | 6582.82 | 7840.81 | 0 | 26,083.7 |
| 124 | Max_nights | Maximum number of nights to be rented | 945.575 | 2604.701 | 3 | 112,030 |
| 125 | Gym | Gym (1: Yes; 0: No) | 0.031 | 0.173 | 0 | 1 |
| 126 | Microwave | Microwave available (1: Yes; 0: No) | 0.249 | 0.433 | 0 | 1 |
| 127 | Doorman | Doorman existence (1: Yes; 0: No) | 0.1 | 0.3 | 0 | 1 |
| 128 | has_dismissed_ib_salmon_flow | Has dismissed the Instant Booking for salmon flow (1: Yes; 0: No) | 0.194 | 0.396 | 0 | 1 |
| 129 | Shower_chair | Roll in shower with chair (1: Yes; 0: No) | 0.007 | 0.084 | 0 | 1 |
| 130 | Outlet_covers | Outlet covers existence (1: Yes; 0: No) | 0.026 | 0.159 | 0 | 1 |
| 131 | Single_level_home | Single level home (1: Yes; 0: No) | 0.054 | 0.226 | 0 | 1 |
| 132 | Waterfront | Waterfront located (1: Yes; 0: No) | 0.097 | 0.296 | 0 | 1 |
| 133 | Dist_port | Distance to the ship port | 24,554.73 | 18,443.67 | 187.8 | 50,277.2 |
| 134 | Suitable_for_events | Suitable for events (1: Yes; 0: No) | 0.039 | 0.195 | 0 | 1 |
| 135 | Patio_or_balcony | Patio or balcony existence (1: Yes; 0: No) | 0.131 | 0.338 | 0 | 1 |
| 136 | Ethernet_connection | Ethernet connection available (1: Yes; 0: No) | 0.043 | 0.203 | 0 | 1 |
| 137 | Room_darkening | Room darkening shades available (1: Yes; 0: No) | 0.152 | 0.359 | 0 | 1 |
| 138 | Check_in_flexible | Flexible check in is allowed (1: Yes; 0: No) | 0.32 | 0.466 | 0 | 1 |
| 139 | Dishes | Dishes and silverware available (1: Yes; 0: No) | 0.265 | 0.441 | 0 | 1 |
| 140 | Window_guards | Window guards existence (1: Yes; 0: No) | 0.032 | 0.176 | 0 | 1 |
| 141 | Pets_living | Pets live on the property (1: Yes; 0: No) | 0.042 | 0.2 | 0 | 1 |
| 142 | Game_console | Game console available (1: Yes; 0: No) | 0.009 | 0.094 | 0 | 1 |
| 143 | Lock_on_bedroom | Lock on bedroom door (1: Yes; 0: No) | 0.128 | 0.334 | 0 | 1 |
| 144 | Reviewee_count | Host’s review count | 60.75 | 102.947 | 0 | 1085 |
| 145 | Fireplace_guards | Fireplace guards (1: Yes; 0: No) | 0.005 | 0.073 | 0 | 1 |
| 146 | Italian | The host speaks Italian (1: Yes; 0: No) | 0.11 | 0.313 | 0 | 1 |
| 147 | IB | Instant bookable allowed (1: Yes; 0: No) | 0.529 | 0.499 | 0 | 1 |
| 148 | Everyone | Instant bookable allowed for everyone (1: Yes; 0: No) | 0.432 | 0.495 | 0 | 1 |
| 149 | Disabled_parking | Disabled parking spot (1: Yes; 0: No) | 0.015 | 0.124 | 0 | 1 |
| 150 | Changing_table | Changing table available (1: Yes; 0: No) | 0.013 | 0.113 | 0 | 1 |
References
- Bakker, M.; Twining-Ward, L. Tourism and the Sharing Economy; World Bank: Washington, DC, USA, 2018. [Google Scholar]
- Gibbs, C.; Guttentag, D.; Gretzel, U.; Morton, J.; Goodwill, A. Pricing in the sharing economy: A hedonic pricing model applied to Airbnb listings. J. Travel Tour. Mark. 2017, 12, 1–11. [Google Scholar] [CrossRef]
- Espinet, J.M.; Sáez, M.; Coenders, G.; Fluvià, M. Effect on prices of the attributes of holiday hotels: A hedonic prices approach. Tour. Econ. 2003, 9, 165–177. [Google Scholar] [CrossRef]
- Thrane, C. Hedonic Price Models and Sun-and-Beach Package Tours: The Norwegian Case. J. Travel Res. 2005, 43, 302–308. [Google Scholar] [CrossRef]
- Ert, E.; Fleischer, A.; Magen, N. Trust and reputation in the sharing economy: The role of personal photos in Airbnb. Tour. Manag. 2016, 55, 62–73. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, K. Consumer valuation of Airbnb listings: A hedonic pricing approach. Int. J. Contemp. Hosp. Manag. 2017, 29, 2405–2424. [Google Scholar] [CrossRef]
- Benítez-Aurioles, B. Why are flexible booking policies priced negatively? Tour. Manag. 2018, 67, 312–325. [Google Scholar] [CrossRef]
- Lorde, T.; Jacob, J.; Weekes, Q. Price-setting behavior in a tourism sharing economy accommodation market: A hedonic price analysis of AirBnB hosts in the caribbean. Tour. Manag. Perspect. 2019, 30, 251–261. [Google Scholar] [CrossRef] [Green Version]
- Teubner, T.; Hawlitschek, F.; Dann, D. Price determinants on Airbnb: How reputation pays off in the sharing economy. J. Self-Gov. Manag. Econ. 2017, 5, 53–80. [Google Scholar]
- Wang, D.; Nicolau, J.L. Price determinants of sharing economy based accommodation rental: A study of listings from 33 cities on Airbnb.com. Int. J. Hosp. Manag. 2017, 62, 120–131. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Kim, J.; Wang, X. Estimating spatial effects on peer-to-peer accommodation prices: Towards an innovative hedonic model approach. Int. J. Hosp. Manag. 2019, 81, 43–53. [Google Scholar] [CrossRef]
- Önder, I.; Weismayer, C.; Gunter, U. Spatial price dependencies between the traditional accommodation sector and the sharing economy. Tour. Econ. 2018, 25, 1150–1166. [Google Scholar] [CrossRef]
- Sanchez, R.P.; Estrada, L.S.; Marti, P.; Mora-Garcia, R.-T. The What, Where, and Why of Airbnb Price Determinants. Sustainability 2018, 10, 4596. [Google Scholar] [CrossRef] [Green Version]
- Chica-Olmo, J.; González-Morales, J.G.; Zafra-Gómez, J.L. Effects of location on Airbnb apartment pricing in Málaga. Tour. Manag. 2020, 77, 103981. [Google Scholar] [CrossRef]
- Chattopadhyay, M.; Mitra, S.K. Do airbnb host listing attributes influence room pricing homogenously? Int. J. Hosp. Manag. 2019, 81, 54–64. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 2010, 28, 281–298. [Google Scholar] [CrossRef]
- Fotheringham, S.; Charlton, M.; Brunsdon, C. The Geography of Parameter Space. Class. IJGIS 2006, 10, 297–325. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.; Brunsdon, C. Two techniques for exploring non-stationarity in geographical data. Geogr. Syst. 1997, 4, 59–82. [Google Scholar]
- Lu, B.; Charlton, M.; Fotheringhama, A.S. Geographically Weighted Regression Using a Non-Euclidean Distance Metric with a Study on London House Price Data. Procedia Environ. Sci. 2011, 7, 92–97. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Jang, S.; Kang, S.; Kim, S. (James) Why are hotel room prices different? Exploring spatially varying relationships between room price and hotel attributes. J. Bus. Res. 2020, 107, 118–129. [Google Scholar] [CrossRef]
- Hernández, J.M.; Suárez-Vega, R.; Santana, Y. The inter-relationship between rural and mass tourism: The case of Catalonia, Spain. Tour. Manag. 2016, 54, 43–57. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, R.J.C.; Han, L.D.; Yang, L. Key Factors Affecting the Price of Airbnb Listings: A Geographically Weighted Approach. Sustainability 2017, 9, 1635. [Google Scholar] [CrossRef] [Green Version]
- Hocking, A.R.R. The Analysis and Selection of Variables in Linear Regression Published by: International Biometric Society Stable URL: http://www.jstor.org/stable/2529336. Biometrics 1976, 32, 1–49. [Google Scholar] [CrossRef]
- Suárez-Vega, R.; Acosta-González, E.; Casimiro-Reina, L.; Hernández, J.M. Assessing the Spatial and Environmental Characteristics of Rural Tourism Lodging Units Using a Geographical Weighted Regression Model. In Quantitative Methods in Tourism Economics; Springer Science and Business Media LLC: Berlin, Germany, 2012; pp. 195–212. [Google Scholar]
- Fotheringham, A.S.; Kelly, M.; Charlton, M. The demographic impacts of the Irish famine: Towards a greater geographical understanding. Trans. Inst. Br. Geogr. 2012, 38, 221–237. [Google Scholar] [CrossRef]
- Páez, A.; Uchida, T.; Miyamoto, K. A General Framework for Estimation and Inference of Geographically Weighted Regression Models: 2. Spatial Association and Model Specification Tests. Environ. Plan. A Econ. Space 2002, 34, 883–904. [Google Scholar] [CrossRef]
- Páez, A.; Uchida, T.; Miyamoto, K. A General Framework for Estimation and Inference of Geographically Weighted Regression Models: 1. Location-Specific Kernel Bandwidths and a Test for Locational Heterogeneity. Environ. Plan. A Econ. Space 2002, 34, 733–754. [Google Scholar] [CrossRef]
- Da Silva, A.R.; Fotheringham, A.S. The Multiple Testing Issue in Geographically Weighted Regression. Geogr. Anal. 2015, 48, 233–247. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M. Some Notes on Parametric Significance Tests for Geographically Weighted Regression. J. Reg. Sci. 1999, 39, 497–524. [Google Scholar] [CrossRef]
- Leung, Y.; Mei, C.-L.; Zhang, W.-X. Statistical Tests for Spatial Nonstationarity Based on the Geographically Weighted Regression Model. Environ. Plan. A Econ. Space 2000, 32, 9–32. [Google Scholar] [CrossRef]
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. J. Stat. Softw. 2015, 63, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Wright, J.; Brownlee, A.; Buswell, R. A comparison of approaches to stepwise regression on variables sensitivities in building simulation and analysis. Energy Build. 2016, 127, 313–326. [Google Scholar] [CrossRef] [Green Version]
- Eugenio-Martin, J.L.; Cazorla-Artiles, J.M.; González-Martel, C. On the determinants of Airbnb location and its spatial distribution. Tour. Econ. 2019, 25, 1224–1244. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Zhou, Y.; Ma, J.; Scott, N. Price Determinants of Airbnb Listings: Evidence from Hong Kong. Tour. Anal. 2019, 24, 227–242. [Google Scholar] [CrossRef]
- Lu, B.; Harris, P.; Charlton, M.; Brunsdon, C. The GWmodel R package: Further topics for exploring spatial heterogeneity using geographically weighted models. Geo. Spat. Inf. Sci. 2014, 17, 85–101. [Google Scholar] [CrossRef]








| Step | Variable | AICc | Adj-R2 | Bandwidth | |||
|---|---|---|---|---|---|---|---|
| 1 | Bathrooms | 1963.745 | 0.494 | 42 | |||
| 2 | Pool | 1790.498 | −173.247 | 0.536 | 42 | ||
| 3 | Bedrooms | 1639.400 | −151.098 | −324.346 | 0.573 | 38 | |
| 4 | #Properties | 1540.275 | −99.125 | −250.224 | −423.471 | 0.597 | 38 |
| 5 | Dryer | 1492.159 | −48.116 | −147.241 | −298.339 | 0.611 | 38 |
| 6 | Dist_Telde | 1454.810 | −37.349 | −85.465 | −184.590 | 0.620 | 38 |
| 7 | Cancel_policy | 1432.370 | −22.440 | −59.789 | −107.905 | 0.630 | 38 |
| 8 | Hot_tub | 1415.896 | −16.474 | −38.914 | −76.263 | 0.629 | 47 |
| 9 | Dist_LPGC | 1400.980 | −14.916 | −31.390 | −53.829 | 0.634 | 47 |
| 10 | German | 1396.044 | −4.937 | −19.852 | −36.326 | 0.639 | 48 |
| 11 | Essentials | 1394.066 | −1.978 | −6.915 | −21.830 | 0.636 | 56 |
| 12 | Air_conditioning | 1381.863 | −12.203 | −14.181 | −19.118 | 0.629 | 74 |
| 13 | Beds | 1365.200 | −16.663 | −28.866 | −30.844 | 0.638 | 69 |
| 14 | Reviews_count | 1354.847 | −10.352 | −27.016 | −39.219 | 0.642 | 69 |
| 15 | Beach500m | 1348.687 | −6.160 | −16.512 | −33.175 | 0.642 | 74 |
| 16 | Wireless_Internet | 1345.877 | −2.810 | −8.970 | −19.323 | 0.643 | 79 |
| 17 | TV | 1338.540 | −7.336 | −10.147 | −16.307 | 0.647 | 79 |
| 18 | Dist_Airp | 1333.869 | −4.672 | −12.008 | −14.818 | 0.649 | 81 |
| 19 | Comp500m | 1328.440 | −5.429 | −10.101 | −17.437 | 0.646 | 92 |
| 20 | Elevator | 1324.574 | −3.865 | −9.294 | −13.966 | 0.643 | 109 |
| 21 | French | 1319.847 | −4.728 | −8.593 | −14.022 | 0.646 | 109 |
| 22 | Beach200m | 1313.561 | −6.285 | −11.013 | −14.878 | 0.645 | 117 |
| 23 | Is_superhost | 1309.226 | −4.335 | −10.621 | −15.348 | 0.645 | 128 |
| 24 | Extra_pillows | 1307.198 | −2.028 | −6.363 | −12.649 | 0.646 | 131 |
| 25 | Cable_TV | 1302.679 | −4.519 | −6.547 | −10.882 | 0.648 | 134 |
| 26 | Hair_dryer | 1301.445 | −1.234 | −5.753 | −7.781 | 0.650 | 134 |
| 27 | Kitchen | 1300.534 | −0.911 | −2.145 | −6.664 | 0.651 | 134 |
| 28 | Dishwasher | 1300.041 | −0.493 | −1.404 | −2.638 | 0.640 | 202 |
| 29 | Security_deposit | 1294.207 | −5.833 | −6.327 | −7.238 | 0.641 | 206 |
| 30 | Cooking_basics | 1289.985 | −4.222 | −10.055 | −10.549 | 0.643 | 206 |
| 31 | Family_kid_friendly | 1286.977 | −3.008 | −7.230 | −13.064 | 0.644 | 206 |
| 32 | Smoking_allowed | 1282.972 | −4.005 | −7.014 | −11.236 | 0.646 | 206 |
| 33 | BBQ_grill | 1279.484 | −3.488 | −7.493 | −10.501 | 0.647 | 206 |
| 34 | Exp_guest+Govid | 1276.782 | −2.702 | −6.190 | −10.195 | 0.649 | 206 |
| 35 | Polish | 1276.108 | −0.674 | −3.376 | −6.864 | 0.650 | 206 |
| 36 | Pict_500m | 1275.365 | −0.743 | −1.417 | −4.119 | 0.648 | 225 |
| Step | Variable | AICc | Adj-R2 | Bandwidth | |||
|---|---|---|---|---|---|---|---|
| 1 | Bathrooms | 1963.746 | 0.494 | 42 | |||
| 2 | Pool | 1790.498 | −173.247 | 0.536 | 42 | ||
| 3 | Bedrooms | 1642.354 | −148.144 | −321.392 | 0.572 | 39 | |
| 4 | #Properties | 1542.882 | −99.472 | −247.616 | −420.864 | 0.596 | 39 |
| 5 | Pict_1km | 1493.958 | −48.925 | −148.397 | −296.541 | 0.609 | 38 |
| 6 | Dryer | 1445.602 | −48.356 | −97.281 | −196.753 | 0.621 | 40 |
| 7 | Suitable_for_events | 1410.584 | −35.017 | −83.373 | −132.298 | 0.633 | 39 |
| 8 | Beds | 1399.254 | −11.330 | −46.348 | −94.704 | 0.640 | 39 |
| 9 | Dist_beach | 1391.136 | −8.118 | −19.448 | −54.466 | 0.645 | 39 |
| 10 | Cancel_policy | 1384.210 | −6.926 | −15.044 | −26.374 | 0.653 | 39 |
| 11 | Essentials | 1380.696 | −3.514 | −10.440 | −18.558 | 0.640 | 56 |
| 12 | Air_conditioning | 1364.979 | −15.717 | −19.231 | −26.157 | 0.635 | 69 |
| 13 | Dist_Airp | 1346.458 | −18.521 | −34.238 | −37.752 | 0.640 | 70 |
| 14 | French | 1334.715 | −11.743 | −30.264 | −45.981 | 0.645 | 69 |
| 15 | Reviews_count | 1319.490 | −15.225 | −26.968 | −45.488 | 0.650 | 69 |
| 16 | Hot_tub | 1315.907 | −3.584 | −18.808 | −30.551 | 0.654 | 69 |
| 17 | Indoor_fireplace | 1310.376 | −5.531 | −9.114 | −24.339 | 0.657 | 69 |
| 18 | Beach500m | 1307.830 | −2.546 | −8.077 | −11.660 | 0.654 | 77 |
| 19 | Elevator | 1304.841 | −2.989 | −5.535 | −11.066 | 0.657 | 77 |
| 20 | Bed_linens | 1304.117 | −0.725 | −3.714 | −6.260 | 0.649 | 103 |
| 21 | Smoke_detector | 1295.905 | −8.212 | −8.937 | −11.926 | 0.650 | 109 |
| 22 | Dist_LPGC | 1289.917 | −5.988 | −14.200 | −14.924 | 0.652 | 109 |
| 23 | Comp500 | 1285.087 | −4.830 | −10.818 | −19.030 | 0.656 | 105 |
| 24 | TV | 1281.761 | −3.325 | −8.156 | −14.143 | 0.654 | 117 |
| 25 | Breakfast | 1274.378 | −7.383 | −10.709 | −15.539 | 0.647 | 165 |
| 26 | Beach201_500 | 1266.657 | −7.721 | −15.104 | −18.430 | 0.648 | 169 |
| 27 | Dishwasher | 1260.417 | −6.241 | −13.961 | −21.345 | 0.650 | 169 |
| 28 | Is_superhost | 1253.886 | −6.530 | −12.771 | −20.492 | 0.650 | 180 |
| 29 | German | 1247.034 | −6.853 | −13.383 | −19.623 | 0.652 | 180 |
| 30 | Dist_Telde | 1242.425 | −4.609 | −11.461 | −17.991 | 0.654 | 180 |
| 31 | Hair_dryer | 1238.286 | −4.139 | −8.747 | −15.600 | 0.655 | 180 |
| 32 | Security_deposit | 1235.656 | −2.631 | −6.769 | −11.378 | 0.657 | 180 |
| 33 | Exp_guest+Govid | 1232.561 | −3.095 | −5.725 | −9.864 | 0.657 | 179 |
| 34 | Lockbox | 1229.881 | −2.680 | −5.775 | −8.405 | 0.660 | 180 |
| 35 | Cooking_basics | 1227.535 | −2.346 | −5.026 | −8.120 | 0.657 | 207 |
| 36 | Refrigerator | 1225.316 | −2.219 | −4.565 | −7.245 | 0.658 | 207 |
| 37 | Beach1000m | 1223.183 | −2.133 | −4.352 | −6.698 | 0.660 | 204 |
| 38 | Polish | 1222.020 | −1.163 | −3.296 | −5.515 | 0.661 | 202 |
| 39 | Kitchen | 1220.408 | −1.612 | −2.775 | −4.908 | 0.662 | 202 |
| 40 | Spanish | 1219.692 | −0.716 | −2.328 | −3.491 | 0.663 | 206 |
| SW-OLS | SW-OLS-GWR | Pre-SW-GWR | SW-GWR | |
|---|---|---|---|---|
| #Variables | 57 | 57 | 36 | 40 |
| Bandwidth | 2259 | 800 | 225 | 206 |
| AICc | 1425.459 | 1346.583 | 1275.365 | 1219.692 |
| Adjusted R2 | 0.603 | 0.623 | 0.648 | 0.663 |
| Adjusted α | 0.05 | 0.0191 | 0.0066 | 0.0063 |
| Average significant variables | 50 | 25.854 | 12.021 | 12.549 |
| Min. significant variables | 50 | 15 | 2 | 2 |
| Max. significant variables | 50 | 41 | 33 | 28 |
| IQR significant variables | 0 | 14 | 12 | 13 |
| #OLS solved models | 11,325 | 13,584 | 3,259,737 | 12,040,470 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suárez-Vega, R.; Hernández, J.M. Selecting Prices Determinants and Including Spatial Effects in Peer-to-Peer Accommodation. ISPRS Int. J. Geo-Inf. 2020, 9, 259. https://doi.org/10.3390/ijgi9040259
Suárez-Vega R, Hernández JM. Selecting Prices Determinants and Including Spatial Effects in Peer-to-Peer Accommodation. ISPRS International Journal of Geo-Information. 2020; 9(4):259. https://doi.org/10.3390/ijgi9040259
Chicago/Turabian StyleSuárez-Vega, Rafael, and Juan M. Hernández. 2020. "Selecting Prices Determinants and Including Spatial Effects in Peer-to-Peer Accommodation" ISPRS International Journal of Geo-Information 9, no. 4: 259. https://doi.org/10.3390/ijgi9040259
APA StyleSuárez-Vega, R., & Hernández, J. M. (2020). Selecting Prices Determinants and Including Spatial Effects in Peer-to-Peer Accommodation. ISPRS International Journal of Geo-Information, 9(4), 259. https://doi.org/10.3390/ijgi9040259