Multitemporal Analysis of Gully Erosion in Olive Groves by Means of Digital Elevation Models Obtained with Aerial Photogrammetric and LiDAR Data

Abstract

Gully erosion is one of the main processes of soil degradation, representing 50%–90% of total erosion at basin scales. Thus, its precise characterization has received growing attention in recent years. Geomatics techniques, mainly photogrammetry and LiDAR, can support the quantitative analysis of gully development. This paper deals with the application of these techniques using aerial photographs and airborne LiDAR data available from public database servers to identify and quantify gully erosion through a long period (1980–2016) in an area of 7.5 km² in olive groves. Several historical flights (1980, 1996, 2001, 2005, 2009, 2011, 2013 and 2016) were aligned in a common coordinate reference system with the LiDAR point cloud, and then, digital surface models (DSMs) and orthophotographs were obtained. Next, the analysis of the DSM of differences (DoDs) allowed the identification of gullies, the calculation of the affected areas as well as the estimation of height differences and volumes between models. These analyses result in an average depletion of 0.50 m and volume loss of 85000 m³ in the gully area, with some periods (2009–2011 and 2011–2013) showing rates of 10,000–20,000 m³/year (20–40 t/ha*year). The manual edition of DSMs in order to obtain digital elevation models (DTMs) in a detailed sector has facilitated an analysis of the influence of this operation on the erosion calculations, finding that it is not significant except in gully areas with a very steep shape.

1. Introduction

Globally, soil erosion is one of the most disturbing phenomena of environmental degradation [1,2]. The degraded arable area worldwide accounts for 39% of the total land suitable for agriculture [3], a percentage that might be increased significantly in coming decades due to the acceleration of erosion caused by global warming [4]. Soil water erosion is a complex process that must be addressed at multiple spatial and temporal scales. There are studies, carried out on a plot scale, in which the physical processes of laminar and rill erosion predominate [5]. Usually, empirical measurements [6] or different variants of the RUSLE (Revised Unified Soil Loss Equation) model [7,8,9] have been applied in these case studies.

Meanwhile, some authors [10] demonstrate that concentrated flow processes such as gully erosion could explain between 50% and 90% of total erosion at basin scales. Gully erosion is one of the most important soil degradation processes, although it has not received much attention until recent years due to the difficulty of its study. Now it is a fast-growing field [11]. Gullies develop at different spatial and temporal scales. They range from ephemeral gullies with sections of less than 1 m², lengths of around 10 m and persistence less than an annual cycle, to large permanent gullies with sections of hundreds of m², several km of development and decades of persistence [10].

Geomatics techniques can support the precise geometric characterization of gully systems since these techniques allow the capture and acquisition of images and ground points coordinates at different spatiotemporal resolutions. Discrete points in gully data surveys can be measured with several methods and instruments such as total station, TS [12,13,14,15,16,17,18], global navigation satellite systems (GNSS) [19,20,21,22,23], or laser altimeters and laser distance meters [16,17,24], although these techniques are generally costly in time and resources. Meanwhile massive point clouds can be captured with Light Detection and Ranging (LiDAR) techniques such as terrestrial laser scanner (TLS) [15,16,21,22,25,26,27], and aerial laser scanner (ALS) [15,22,23,26,28,29,30,31,32,33]. Besides, images can be acquired by means of digital cameras and sensors, in many occasions combined with some point capture techniques. Thus, there are many studies based on images of different resolution and precision, captured with different platforms, from close range [20,34,35] and terrestrial systems [16,23,36,37,38,39,40] to airborne systems using kites [41], unmanned aerial vehicles, UAV [21,23,24,39,42,43,44], conventional aerial platforms [15,19,20,22,28,29,32,33,37,40,43,45,46,47,48,49] or satellites [21,50,51].

Images and orthoimages can be used for surface characterization, so conventional aerial orthophotographs or high-resolution satellite images can suffice for these applications [15,29,33,43,49]. This has allowed to estimate the lengths, widths and densities of the gully systems, analyzing their evolution over time and specifically the displacements or lateral growth of some gullies [15,32,40,43,49,52]. In some cases, the influence of determinant factors on the formation and development of the gullies are analyzed, which allows the application of predictive models [33,43,53,54,55,56].

In addition to planimetric studies, image-based methods permit the generation of digital elevation models (DEMs) for the estimation of gully depths and volumes as well as their variations. Thus, different approaches have been applied, either based on conventional photogrammetric techniques [19,20,24,32,37,45,46,47,48,49] or new computer vision techniques such as Structure from Motion, SfM, and Multi Video Stereo, MVS [21,23,25,38,39]. The availability of models at different epochs leads to multitemporal analysis of gully systems by comparing these models in order to obtain differential models (DEMs of Differences or DoDs). These models can be derived from conventional aerial photogrammetry, which has recently undergone a great development in this field [20,28,32,38,39,40,44]. This approach allows us to survey relatively large areas with high resolutions and also to carry out time-based studies from historical flights available since the mid-20th century [20,28,29,32,47,52]. All of these image-based methods are often combined with point capture techniques such as LiDAR [15,23,29,36], GNSS [20,22,23,45] or conventional surveying [11,15,16,49]. The use of LiDAR leads to the generation of high resolution and reliable DEMs [15,22,25,26,28,32,33,38] and enables us to obtain digital terrain models (DTMs) by classifying and filtering the high-density point clouds.

In addition, Unmanned Aerial Vehicles (UAVs) are well suited for very high resolution and precise surveys in areas of about 0.01 to 100 km². UAVs are very suitable for intermediate scales between terrestrial techniques (GNSS, close range photogrammetry and TLS) and aerial or space surveys (conventional aerial photogrammetry, LiDAR and VHR satellite imagery) but keeping low or moderate costs and allowing high temporal resolution studies. Most of the current studies using multicopter UAVs are of centimeter resolution [21,23,25,38,39,44].

All these geomatics approaches lead to three-dimensional measurements of gullies’ width, depth and cross-sectional areas from which volumetric estimations are made [14,16,17,23,27,36,50]. They have enabled to determine that gully soil losses at least doubled the rates measured in experimental plots or RUSLE models [49]. However, the most appropriate approach is to generate digital elevation models, both DSMs and DTMs (filtered and/or edited) of high resolution and precision [15,20,21,22,23,24,25,28,29,32,34,38,39,40,41,42,45,46,47,48,51]. Based on these DEMs, morphometric measurements and volumetric estimations can also be performed [15,20,21,28,32,33,38,39,40,41,42,45,46,47,48].

A crucial aspect in these studies is the accuracy or quality of the data collected with the different techniques, since the validity of the results is strongly linked to it. Accuracy analysis can be made from qualitative visual observations but also from different quantitative methods [16,32,41]. In some cases the accuracy can be estimated from errors (usually the root mean square or RMS) of the image orientation or the laser point cloud registration processes, at ground control and/or check points [14,21,23,32,39,40,41,42,43,47,48,57,58]. Other accuracy analyses are those based on the comparison of the height of profile points or DEMs, with respect to points measured with a more accurate method such as the TS/GNSS [15,20,23,37,39,42,45] or TLS [16,25,38]. Finally, methods based on the comparison of repeated measurements of the same surface can be found, generally by calculating the standard deviation of these measures in a sample of points [13,19,26,35,57]. Moreover, sometimes the error analyses extend from the DEMs to the DoDs derived from them [13,19,30,57,58].

This paper aims to describe a methodology for the identification and quantification of gully erosion through a long period (1980–2016), based on aerial photogrammetry and LiDAR techniques. For this objective, only those data available on public spatial data infrastructures (SDI) or download servers have been used. Ground control points (GCPs) from the LiDAR point clouds were extracted, allowing the alignment of historical photogrammetric flights in the same common coordinate reference system without the need for field surveyed GCPs, although some check points were measured with GNSS in the field in order to monitor the whole process. From these flights, DSMs, DTMs and differential models (DoDs) were generated in order to analyze the effects of gully erosion on olive groves in a selected study area of 7.5 km² in the province of Jaén (Southern Spain). This methodology has been validated by means of the estimation of errors and uncertainties from the models obtained. The analysis has been addressed calculating the height differences and volumes between models and their corresponding rates along the different periods considered. Furthermore, a detailed area where the erosion processes are more intense was considered to monitor the gully evolution and to study the relationships with the rainfalls as triggering factor. Finally, to complete the validation analysis and limitations of the methodology employed, DSMs were edited to obtain DTMs, comparing the results obtained in both approaches.

2. Materials and Methods

2.1. Study Area

The study area, with an extension of approximately 7.5 km², is located in the western part of the province of Jaén (Andalusia, Spain), at a distance of about 25 km from the province capital (Figure 1a,b). It has an altitude of between 355 m and 565 m and an average slope of 5.37°. It is located within the natural region of the Eastern Guadalquivir river basin, which includes the headwater areas from Cazorla and Segura Ranges. Discarding the Betic Mountains to the south, the basin varies in altitude from about 200 to 1000 m, with slopes generally below 10°.

From the geological point of view, this basin is made up of the Guadalquivir Units [59], a set of materials of diverse lithology tectonically intercalated with autochthonous loamy-clay marine sediments from the Miocene age (Figure 1b). The predominant allochthonous lithologies are Triassic lutites, evaporites and carbonates, as well as Cretaceous-Paleogene marls and clays. Specifically, in the study area, Triassic and Miocene materials outcrop (Figure 1c). Triassic units comprise lutites and sandstones with subsidiary amounts of carbonates and gypsum as metric tectonic slices. Miocene sediments consist of white marls and marly silts [60].

The area is affected by intense erosion, both laminar and gully, in addition to other superficial processes such as landslides [57,61]. Some sections of the gully area studied, which sometimes affect rural roads and paths (Figure 2c), are shown in Figure 2.

The province of Jaén is the area with the largest extension of olive groves in the world. It occupies 48% of the arable area of the province [62] and represents 59% of the surface of this crop in Spain, 30% in Europe and 19% in the world [63]. The olive grove connects the economic, cultural and social life of the province, being also its most emblematic landscape. However, its sustainability is exposed to several threats, mainly due to the intensification of the crop, which has reduced the quality of the soils in recent decades [64]. Thus, the traditional alternation of Mediterranean crops between cereal and olive is being replaced by a monoculture of the olive grove, affecting the soil´s ability to support the agricultural production along with environmental protection and human health and well-being. Currently water erosion is the main cause of soil degradation in the olive grove, as happens in the province of Jaén whose affected area has become the largest in Andalusia and Spain. Thus, 80% of the Jaén olive grove has erosion rates above 10 t/ha*year, with an average value of 32 t/ha*year [65], which means losses far exceeding the capacity for natural regeneration of the soil [7]. Erosive processes also represent an economic loss, especially related to the reduction of soil productivity but also with other effects such as the filling of reservoirs and damage to infrastructures [66].

2.2. Materials

The methodology focuses on the use of photogrammetry techniques with data captured from conventional aerial platforms with sub-metric resolution, accomplished by LiDAR data. A set of historical flights from 1980 [67], 1996 and 2001 [68], 2005, 2009 2011, 2013 and 2016 [67] obtained from different cartographic agencies have been processed (

Table 1. Properties of the images and LiDAR data sets.

Camera and image properties
Date	Bands	Format	Scale	Camera	Digitalization resolution (mm)	GSD (m)
1980	Panchromatic	Film	1:18,000	Wild RC10	0.025	0.27
1996	Panchromatic	Film	1:20,000	Wild RC10	0.020	0.30
2001	Panchromatic	Film	1:20,000	Leica RC30	0.015	0.30
2005	CIR	Film	1:30,000	Leica RC30	0.015	0.45
2009	RGB-NIR	Digital	1:30,000	Z/I DMC120	---	0.45
2011	RGB-NIR	Digital	1:30,000	Z/I DMC120	---	0.45
2013	RGB-NIR	Digital	1:30,000	Vexcel UCXp	---	0.45
2016	RGB-NIR	Digital	1:30,000	Vexcel UCXp	---	0.45
LiDAR data set
Date	System	Flying Height m (above sea level, asl)			points/m2
2014	Leica ALS60	2700			0.5–1

). The image ground sample distance (GSD) of the different flights varies from of 0.27 m in the 1980 flight to 0.30 m in the 1996 and 2001 flights, and 0.45 m in the remaining flights from 2005 to 2016. The 1980, 1996, 2001 and 2005 flights are analog (film-based cameras). The 2005 flight is a Color Infrared (CIR) flight, while the 1977, 1996 and 2001 flights are panchromatic. Original film images had been digitized at different scanning resolutions between 1000 and 1700 ppi, which has implied different image pixel sizes of 0.015–0.025 mm. The remaining flights (2009, 2011, 2013 and 2016) are digital and color-near infrared (RGB-NIR). In addition, the LiDAR data correspond to the first national LiDAR cover, which in Andalusia was captured in 2014 with a resolution of 1 point/m².

Both photogrammetric and LiDAR data are available from several public Spatial Data Infrastructures and download services. Thus, photographs of the national flights (Interministerial and PNOA flights) are available with different image formats (TIFF/JPG/ECW) in the photo-library of the National Geographic Institute of Spain (IGN) [67], and the photographs of the regional flights in the photo-library of Andalusia [68]. Finally, the LIDAR data, stored as tiles (2 x 2 km) in ASPRS LAS format, can be accessed via the download service of IGN [69]. These data consisted of a previously classified point cloud. Raw LiDAR data were not available in the download service.

2.3. Methodology

The methodology summarized in Figure 3 consists of several phases partially described in previous papers [57,58,70]:

• Orientation of the historical flights.
• Generation of the DSMs and orthophotographs.
• Calculation of DSMs of differences (DoDs).
• Delimitation of gully areas and DSMs edition of detailed area.
• Estimation of height differences and volumes between models.

2.3.1. Orientation of the Historical Flights

First, the LiDAR point cloud was obtained by merging the corresponding 2 x 2 km tiles, downloaded from the above-mentioned service. Data consisted of a classified point cloud of 1 point/m² density. Thus, both artefacts and noise had previously been corrected, which was confirmed by means of a visual inspection. Nevertheless, in order to control the quality of the LiDAR data and to develop an approach to extracting reliable control points from the LiDAR point cloud, a set of 21 check points well defined in the point cloud was measured in the field with differential GNSS techniques. These points had to be unequivocally identifiable features (for example constructions and building roof corners). Thus, some agricultural buildings and sheds with flat roofs were selected, and the roof corners were measured with GNSS techniques. Since these corners could not be accurately identified in the LiDAR point cloud due to the low data density, the coordinates of the roof corners had to be computed from the LiDAR data themselves.

Thus, the corners were obtained by adjusting a flat surface to the LiDAR points located on the roofs and computing the minimum bounding rectangle (MBR). Figure 4 shows this process. Then these corners were compared with the field-measured ones.

Table 2. Error of LiDAR point cloud regarding GNSS-based check points ¹.

Statistic	X	Y	XY	Z
Minimum	−0.655	−0.808	0.256	−0.067
Maximum	0.686	1.442	1.521	1.915
Mean	0.090	0.179	0.649	0.236
Standard deviation	0.405	0.591	0.337	0.403
RMS	0.405	0.604	0.727	0.459

¹ Errors are expressed in m.

shows the results of this comparison. The overall mean X and Y errors are lower than 0.20 m while the root mean square (RMS) and standard deviation (SD) are about 0.50 m; combined, mean and RMS horizontal (XY) errors are of about 0.7 m. Meanwhile, vertical (Z) errors are the following: mean, 0.24 m; SD, 0.40 m and RMS, 0.46 m.

These results validate the methodology developed to obtain ground control points in order to align and georeferenced the aerial images. Thus, from this point cloud, a set of additional photogrammetric ground control points (GCP) and check points (CHK) was extracted according to the following criteria:

• The points should be well distributed throughout the study area.
• They should be unequivocally identifiable features (artifacts and constructions).
• They should remain stable and visible in most of the flights considered.

Although corners and identifiable details could have been measured accurately in the images and the field to be used as conventional GCPs, these points were extracted from the LiDAR data, as indicated in the preceding paragraphs. Since all data are available from public download services, the approach used in this study can be applied without the need of using field-measured GCP/CHK points, and then, historical flights can be oriented using only the public LiDAR dataset. Moreover, the use of these second-order GCPs [57,58], extracted from the LiDAR data, has guaranteed that all flights were processed under the same common reference system (ETRS89-UTM 30N).

The GCPs, the flight and camera parameters (camera GNSS positions, inertial IMU data, camera calibration parameters, etc.) and a number of tie points were used in the orientation or alignment process of the historical photogrammetric flights, using a digital photogrammetric workstation (DPW) and the software Socet Set 5.6 [71]. Due to the lack of calibration data in the old analog film-based cameras, approaches for the use of historical flights must be considered [72,73].

Table 3. Errors of orientation process at control (GCP) and check (CHK) points ¹.

Date	Image Number	GCP/CHK Number	Tie Points Number	RMS Pixel	RMS GCP		RMS CHK		RMS Prop.
					XY	Z	XY	Z	XY	Z
1980	3	7/11	97	0.187	0.729	0.271	0.397	0.460	0.828	0.650
1996	3	8/13	105	0.266	0.507	0.024	0.545	0.809	0.908	0.930
2001	3	10/15	97	0.256	0.768	0.123	0.396	0.367	0.828	0.588
2005	3	12/13	145	0.422	0.691	0.165	0.508	0.706	0.887	0.842
2009	3	14/16	143	0.148	0.578	0.159	0.473	0.247	0.868	0.521
2011	3	13/12	147	0.147	0.575	0.167	0.533	0.664	0.901	0.807
2013	3	16/18	127	0.129	0.675	0.092	0.398	0.832	0.829	0.950
2016	3	18/25	123	0.166	0.545	0.182	0.361	0.632	0.812	0.781

¹ RMS errors are expressed in m.

shows the main parameters of the photogrammetric process and the errors involved, both in the GCP and in the CHK points. The XY errors range between 0.50 and 0.80 m in the GCP and 0.40–0.55 m in the CHK. Meanwhile, Z errors are lower than 0.16 m (except for the 1980 flight where it reaches a value near to 0.3 m) in GCP, but they present a greater variability in the CHK. Thus, the values are of 0.25 m in the 2009 flight; 0.37 m in the 2001 flight; 0.46 m in the 1980 flight; 0.60–0.70 m in the 2005, 2011 and 2016 flights and 0.80–0.85 m in the 1996 and 2013 flights.

Taking into account that the LiDAR control points used in the orientation process are affected by the errors shown in Table 2, the propagation error can be computed in the check points by means of Equation (1):

Prop YEAR = (RMS LiDAR 2 + RMS PHOTO − YEAR 2) 0.5

(1)

Thus, the propagated errors in the horizontal (XY) component range from 0.80 to 0.90 m. Meanwhile, in the vertical (Z) component, they range from 0.50 to 0.65 in the 1980, 2001 and 2008 flights and from 0.80 to 0.95 m in the 1996, 2005, 2011, 2013 and 2016 flights.

2.3.2. Generation of DSMs and Orthophotographs

Digital surface models (DSM) and orthophotographs for each flight were generated using automatic correlation techniques (dense matching) implemented with the NGATE (Next Generation Automated Terrain Extraction) module of Socet Set 5.6 [71,74]. A DEM resolution of 5 times (2.5 m) the value of the original imagery GSD (0.5 m) has been considered, according the conventional norm in photogrammetry of using a multiple value of GSD for DEM generation. At present, this rule is gradually being reduced due to the improvements on new algorithms for dense matching and the use of patterns of photogrammetric flights with higher overlaps, as those planned with unmanned aerial systems (UAS). From the DSMs generated, grids files with point spacing of 2.5 m have been exported in text format. These grids were opened in a GIS software, QGIS 3 [75], and transformed to raster in TIFF format with the same resolution (2.5 m), by means of the rasterization tool of QGIS. Thus, the grid values resulting of the DSM generation were not modified by other raster interpolation methods. Meanwhile, the orthophotographs were exported to a raster format (TIFF), with a GSD equal to the original imagery GSD (0.5 m). The DSM for the LiDAR data and the orthophotographs for the 1980 and 2016 flights are shown in Figure 5.

In this paper, the propagated Z errors calculated at the check points are assumed to be the DSMs uncertainties (

Table 4. Z errors and vertical uncertainties of the models (DSMs and DoDs) ¹.

DSM Date	DSM Uncertainty	Interval	DoD Uncertainty
1980	0.650
1996	0.930	1980–1996	1.135
2001	0.588	1996–2001	1.100
2005	0.842	2001–2005	1.027
2009	0.521	2005–2009	0.990
2011	0.807	2009–2011	0.961
2013	0.950	2011–2013	1.247
2016	0.781	2013–2016	1.230

¹ Errors and uncertainties are expressed in m.

), as will be discussed later.

2.3.3. Calculation of DSMs of Differences (DoDs)

Differential models or DSM of differences (DoDs) have been calculated from the DSMs, which has objectively allowed the detection of the areas that undergo vertical displacements of the ground surface between successive dates. Displacements may be negative or positive, depending on whether each model compared with a reference model lies below or above it, allowing the identification of areas of ground descent (mass erosion or depletion) or ascent (mass accumulation or deposition), respectively.

In this paper as in previous ones [57,58,70], DSMs have been used preferably to DTMs. This is because all the models used for computing DoDs are of photogrammetric origin, and thus, the processes of automatic classification and filtering of point clouds do not ensure good results in areas where there is a certain vegetation cover or other elements. Moreover, editing models in order to obtain DTMs in a wide area would be a very time-consuming process and would not ensure an improvement. Nevertheless, a small area has been edited in order to compare and calibrate the results, as described below. The work with DSMs can produce a distortion in the detection and quantification of the gullies, because some vertical changes are due to vegetation (growing, clearing, etc.), constructions or other elements.

Regarding the vertical uncertainties of the DoDs, they are estimated as follows [19,58,76]:

Unc. DoD YEAR1-YEAR2 = (Unc. DSM YEAR1 2 + Unc. DSM YEAR2 2) 0.5

(2)

The calculated uncertainties for DoDs are around 1 m (Table 4). Based on this uncertainty, firstly a threshold filter of ±1 m was applied in the GIS software for visual identification of the areas affected by erosion processes, discarding those areas with vertical displacements lower than 1 m in absolute value. As will be discussed later, according to [13,19,28,45] this filter eliminates 68% of the uncertainty.

2.3.4. Delimitation of Gully Areas and DSM Edition of Detailed Area

The identification and delimitation of gully areas have been based on a semiautomatic procedure. First the application of the filter defined before, and especially the areas with negative values higher than 1 m (in absolute terms), allows the identification of potential gullies, which will be validated through interpretation of orthophotographs. These areas have been delimited by polygon-drawn tools in the GIS software. The gully network shown in Figure 1c results of the application of this procedure to the complete period analyzed (1980–2016).

Moreover, a detailed sector with an intense progress of the gully in recent years has been edited manually in order to obtain DTM by means of Socet Set, using the stereo tools of the DPW. Specifically, the edition has been applied to the DSMs for which the DoDs were more relevant (2009–2011 and 2011–2013), and it implied vegetation clearing and artifacts deletion. Several tests have been carried out with different resolutions and using or not using break lines in the DTM generation. The results were also exported to grid text files that were opened in the GIS software and transformed to raster in TIFF format by means of the rasterization tool of QGIS. In the same way as before, DoDs are obtained from DTMs.

2.3.5. Estimation of Height Differences and Volumes between Models

The GIS analysis of DoDs allows the estimation of the vertical depletion (erosion) or deposition (accumulation) of soil material. First, the areas affected by gully erosion can be calculated as an estimation of the importance of the process in the whole study area. Moreover, the area of depletion and deposition can be also calculated, considering or not the threshold of uncertainty of ±1 m. These calculations allow a first approach for evaluating the predominance of the depletion or deposition processes.

Meanwhile, the calculation of the mean or average values from the DoD (height differences) in the gully areas allows us to analyze in a deeper way the balance between depletion and deposition processes, estimating the general losses or gains of soil material. If the average balance is negative, the depletion processes predominate, and if it is positive, the deposition processes do. In this case, an approach based on the probability distribution of the errors has been addressed. Thus, according to [13,19,28,45], the average balance of height differences can be estimated by weighting each height difference according to its probability of being free of uncertainty. For instance, height differences greater than ±1 m (±RMS Z) have a probability of 68%, height differences of more than ±2 m (±2RMS Z) have a probability of 95% and so on. The average values of negative (depletion) and positive (deposition) height differences are also calculated, considering in each case the corresponding areas. The rates of depletion, deposition and balance height differences can be estimated by dividing the corresponding values by the time interval between models.

Finally, the volumetric calculations are carried out by means of the GIS software (QGIS), estimating the volume balance of soil material (losses if the balance is negative or gains if the balance is positive) in a given area. In this case, the depletion, deposition and balance volumes are estimated following the same approach based on the probabilities described in the height differences. In the same way, the volume rates can also be calculated by dividing those values by the time interval. Finally, the volume rates have been transformed to mass rates by surface and time (t/ha*year), that is, the units in which the erosion data are usually expressed, dividing by the area in ha and considering an average density of 1.5 t/m³. This is a rounded value taken from the bulk density estimated from 4 undisturbed cylindrical soil cores (5 cm in diameter, 5 cm long) in each one of sections a and c (Figure 2), yielding an average density of 1.512 (±0.201) t/m³.

The height differences and volumes between models were also analyzed in the detailed area for the DSMs as well as the DTMs obtained by means of a manual edition of the DSMs. The analysis with the DTMs has been made in order to validate the results obtained from DSMs. Thus, some tests have been applied to evaluate the influence of model resolution and the use of break lines in the interpolation.

3. Results

In this section, the results of the analysis of DoDs obtained from DSMs, both in the whole area and in the detailed area, are presented. For the whole area, three analysis are made: first we analyze the areas, second the height differences and third the volumes for the complete period (1980–1996) as well as for the partial periods. For the detailed area, the analysis is focused in the height differences and the volumes, also for the complete and the partial periods. Additionally, for the detailed area, an analysis of DODs from edited DTMs has been made, calculating also the height differences and the volumes.

3.1. Areas, Height Differences and Volumes for the Whole Area

The DoDs of the different periods for the whole area are shown in Figure 6. The area affected by gully erosion has an extension of 0.17 km² and represents 2.25% of the study area of 7.45 km². Within it, the distribution of depletion and deposition areas for the different periods is listed in

Table 5. Areas affected by the gullies: depletion and deposition ¹.

Period	With the Uncertainty Area						Without the Uncertainty Area
	Depletion		Deposition		Uncertainty		Depletion		Deposition
	Area	%	Area	%	Area	%	Area	%	Area	%
1980–1996	18794	11.22	22050	13.16	126694	75.62	83438	49.80	84106	50.20
1996–2001	29800	17.79	10625	6.34	127119	75.87	106019	63.28	61525	36.72
2001–2005	8719	5.20	8656	5.17	150169	89.63	66331	39.59	101213	60.41
2005–2009	10731	6.41	12081	7.21	144731	86.38	79669	47.55	87875	52.45
2009–2011	34650	20.68	12731	7.60	120163	71.72	104531	62.39	63013	37.61
2011–2013	19438	11.60	7588	4.53	140519	83.87	90844	54.22	76700	45.78
2013–2016	5706	3.41	9175	5.48	152663	91.12	87819	52.42	79725	47.58
1980–2016	51481	30.73	11650	6.95	104413	62.32	106169	63.37	61375	36.63

¹ All the areas are m².

. As shown in this table, the uncertainty area, where the height differences are in the range of ±1 m, is much larger than the depletion and deposition areas in every period. Meanwhile the depletion and deposition areas have a similar extent in most periods (1980–1996, 2001–2005, 2005–2009 and 2013–2016), except in 1996–2001, 2009–2011 and 2011–2013, when the depletion area is about twice the deposition area. The maximum percentage of depletion area regarding the total gully area considered was reached in 2009–2011. Regarding the whole period analyzed, the percentage of depletion area becomes much larger (31%) than the percentage of deposition area (7%). Discarding the uncertainty area (62% of the total gully area), the percentages reach 63% and 37%, respectively.

The results of the height differences between models (depletion and deposition heights) for the whole area are presented in

Table 6. Height differences and rates in the gullies of the whole study area ^1,2.

Period	Depletion			Deposition			Balance
	Min	Average	Rate	Max	Average	Rate	Average	Rate
1980–1996	−4.182	−0.165	−0.010	3.340	0.174	0.011	0.009	0.001
1996–2001	−4.236	−0.250	−0.050	4.022	0.102	0.020	−0.148	−0.030
2001–2005	−4.880	−0.075	−0.019	4.570	0.097	0.024	0.021	0.005
2005–2009	−4.897	−0.105	−0.026	5.125	0.114	0.029	0.009	0.002
2009–2011	−5.910	−0.356	−0.178	17.984	0.123	0.061	−0.233	−0.117
2011–2013	−14.883	−0.206	−0.103	3.872	0.080	0.040	−0.125	−0.063
2013–2016	−3.615	−0.073	−0.024	4.367	0.093	0.031	0.020	0.007
1980–2016	−6.824	−0.611	−0.017	2.990	0.100	0.003	−0.510	−0.014

¹ Average, minimum and maximum height differences are in m. ² Rates are in m/year.

. Average rates of depletion height differences can be observed of between 0.01 and 0.20 m/year, with the highest values in the periods 1996–2001, 2009–2011 and 2011–2013, being the value for the complete period of 0.02 m/year. Meanwhile, the average rates for deposition height differences are very low for every period (under 0.06 m/year), with a rate for the complete period close to 0. Finally, the rates for balance height differences reach negative values of 0.12 m/year in the period 2009–2011, 0.06 m/year in 2011–2013 and 0.03 m/year in 1996–2001, while the values are practically null in the remaining periods and of 0.014 m/year in the complete period.

The results of volume calculations are shown in

Table 7. Volumes and rates in the gullies of the whole study area ^1,2,3.

Period	Depletion			Deposition			Balance
	Vol.	Vol. R	Mass R	Vol.	Vol. R	Mass R	Vol.	Vol. R	Mass R
1980–1996	−27,644	−1728	−3.48	29,093	1818	3.66	1449	91	0.18
1996–2001	−41,874	−8375	−16.86	17,110	3422	6.89	−24,765	−4953	−9.97
2001–2005	−12,641	−3160	−6.36	16,170	4043	8.14	3529	882	1.78
2005–2009	−17,593	−4398	−8.86	19,115	4779	9.62	1522	380	0.77
2009–2011	−59,614	−29807	−60.01	20,533	10,267	20.67	−39,081	−19,540	−39.34
2011–2013	−34,462	−17231	−34.69	13,464	6732	13.55	−20,997	−10,499	−21.14
2013–2016	−12,164	−4055	−8.16	15,567	5189	10.45	3404	1135	2.28
1980–2016	−102,333	−2843	−5.72	16,803	467	0.94	−85,530	−2376	−4.78

¹ Volumes are in m³; ² Volume rates are in m³/year; ³ Mass rates are t/ha*year.

, where it is observed that the volumes involved in the complete period are about 100,000 m³ for depletion and about 17,000 m³ for deposition processes, which results in a negative balance of waste material of 85,000 m³. The rates are near 2800 m³/year for depletion processes and about 500 m³/year for deposition, with a balance (waste) rate of almost 2400 m³/year in absolute value. Translated to mass rates, the values estimated for the whole period are of almost 8 t/ha*year for depletion processes, 2 t/ha*year for deposition and 5.5 t/ha*year for the balance. However, the volumes and rates vary greatly by periods, and thus, there are periods with larger amounts of material motion such as 2009–2011 and 2011–2013 that present depletion rates of 20,000–30,000 m³/year, deposition rates around 8000–10,000 m³/year and waste rates of 10,000–20,000 m³/year. The remaining periods present depletion rates lower than 10,000 m³/year, deposition rates lower than 5000 m³/year with negative balance rates usually lower than 5000 m³/year. The mass rates present in some periods such as 2009–2011 and 2011–2013 values higher than 30–60 t/ha*year for depletion processes, around 13–20 t/ha*year for deposition processes and between 20 and 40 t/ha*year for the negative balance. The remaining periods present rates lower than 10 t/ha*year for depletion and deposition processes and usually lower than 2 t/ha*year for the balance, except for the period 1996–2001, which almost reaches 10 t/ha*year.

3.2. Height Differences and Volumes for the Detailed Area

The DoDs for the detailed area are shown in Figure 7 for the DSMs and in Figure 8 for the edited DTMs (in the latter, for the periods of higher activity, 2009–2011 and 2011–2013). Meanwhile, the calculations of height differences in the detailed area are shown in Table 8a for the DSMs and in Table 8b for the edited DTMs.

Regarding DSMs (Table 8a), the average rates for depletion height difference are below 0.10 m/year for most periods, except for 2009–2011 and 2011–2013 when the rates reach 0.50 and 0.30 m/year, respectively, 0.05 m/year being the accumulated rate for the complete period. Meanwhile, the rates for deposition show values lower than 0.10 m/year for every period, with the rate for the complete period being close to 0. Finally, the balance height differences present usually rates lower than 0.05 m/year in absolute value, except for 2009–2011 and 2011–2013 when the rates were of −0.40 and −0.30 m/year, respectively, while the balance rate for the complete period was about −0.05 m/year.

The height differences listed in Table 8b for the edited models of the periods 2009–2011 and 2011–2013 show only small differences regarding the values obtained for the models generated automatically, when the break lines are not used. Thus, the rates of depletion height differences reached an average value of 0.54 m/year and 0.33 m/year, respectively, when the resolution is of 2.5 m as well as of 1 m. Meanwhile, the rates for deposition height are below 0.05 m/year, and the balance heights are very similar to those for the depletion. When the resolution is 1 m but break lines are used, the rates for depletion height differences reach 0.75 m/year in the period 2009–2011 and 0.33 m/year in the period 2011–2013. The deposition values maintain values below 0.10 m/year in both periods, thus the balance rates are very similar to the depletion ones in every case.

The results obtained for volume analysis of the detailed area are shown in Table 9a for the DSMs and in Table 9b for the edited DTMs. From Table 9a, it is observed that the depletion and balance (waste) volumes for the whole period (1980–1996) are higher than 30,000 m³ (about a third part of the volumes for the whole area), but the deposition volumes are insignificant. Thus, the volume rate is around 850 m³/year for the depletion processes and the balance that gives a mass rate by surface and time near 50 t/ha*year, being these rates insignificant in deposition processes. By periods, the depletion volumes are larger than the deposition volumes for most periods, which results usually in negative balance (waste volumes). The rates for depletion processes are lower than 1000 m³/year for most of the periods, reaching values of between 6000 and 9000 m³/year in the periods 2009–2011 and 2011–2013, while the deposition rates present values equal to or lower than 1000 m³/year in all the periods. Thus, the balance (waste) rates are usually very low but they reach values of around 6000–7000 m³/year in the periods 2009–2011 and 2011–2013. The mass rates present extreme values (higher than 300 t/ha*year) for depletion processes and the balance in the periods 2009–2011 and 2011–2013, and moderate values (lower than 50 t/ha*year) in the remaining periods. The values for deposition processes are low in all periods.

The volumes computed for the edited models (Table 9b) are also very similar to those calculated from the automatic models, again when break lines are not taken into account. Thus, the rates are near to 10,000 m³/year and 6000 m³/year for depletion volumes in the periods 2009–2011 and 2011–2013, while they are lower than 1000 m³/year for deposition processes. Translated to mass rates, the depletion processes reach extreme values higher than 600 t/ha*year in the period 2009–2011 and higher than 300 t/ha*year in the period 2011–2013, while the deposition processes present rates much lower, about 50 t/ha*year. When the resolution increases to 1 m and break lines are considered, the rates of depletion volumes are of 13,500 m³/year in the period 2009–2011 and of 6000 m³/year in 2011–2013, with the deposition rates under 1000 m³/year. Translated to mass rates, the depletion processes present values of 800 t/ha*year in the period 2009–2011 and 350 t/ha*year in the period 2011–2013, with deposition processes being much lower, 37 t/ha*year and 41 t/ha*year, in the same periods.

4. Discussion

In this section we first present a discussion about the LiDAR and the photogrammetric flights’ uncertainties. After that, we discuss the results obtained from the height differences and volumes in the whole area and in the detailed area. The relationships of erosion rates by periods to the rainfalls are also analyzed. Finally, for the detailed area, the comparison between the results from DSMs and DTMs with different interpolation conditions is discussed.

4.1. Accuracies and Uncertainties

First, a quality control of the LiDAR points cloud was carried out with some field GNSS surveyed points. This control showed that horizontal (XY) mean and RMS errors were around 0.7 m, while the vertical (Z) mean error was of 0.24 m in absolute value, and the RMS and SD errors were about 0.40–0.45 m. From these errors, the uncertainties, estimated as the values of RMS or SD as in previous studies [57,58,70], were of 0.7 m for the horizontal component and 0.5 m for the vertical one. Then the horizontal uncertainty for X and Y would be about 0.5 m for each one, which coincides approximately with half of the LiDAR data resolution and is equal to the orthophotographs resolution. Meanwhile, the mean vertical (Z) error of 0.24 m informs us about a good general fit of the aerial LiDAR point cloud to the ground surface, as the SD or RMS values under 0.5 m do about the good fit of particular points or sectors. Moreover, it is in accordance with some previous studies that have used LiDAR data to study Earth surface processes [15,22,26,28,30,31,33,58,76]. In these papers the accuracy, expressed as an instrumental specification or estimated from comparison of LiDAR data with more precise methods (GNSS, TS, TLS), ranges mostly from 0.1 m to 0.5 m. Lower values can only be obtained by means of TLS surveys, in which the accuracy ranges between 0.02 m and 0.1 m [15,22,25,26].

Regarding the uncertainty of the photogrammetric products (DSMs and orthophotographs), in some previous studies [57,58,77], it has been observed that the vertical uncertainties in DEMs obtained by means of matching from photogrammetric flights are about two or three times the orientation residual errors in Z, calculated in the control points (GCPs). However, in this paper, we have considered a propagation error from LiDAR data to the photogrammetric orientation process using external check points. In general, since an external check has been used, errors have been higher than the estimations of the previously mentioned papers. As can be observed in Table 3 and Table 4, the Z error in check points is higher than two or even three times the Z error in control points. Thus, the RMS errors propagated of the vertical component (Z) show values between 0.5 and 0.9 m, which are assumed as the uncertainties of the DSMs. From these, the uncertainties of DoDs are calculated, resulting in values around 1 m, in the same order of magnitude to those estimated in reference studies with similar methodologies and resolutions [20,28,47,48,58]. Higher accuracies are only obtained when images of higher resolution are processed: 10⁻³ m order and even lower in close-range photogrammetry [20,34,36]; 10⁻² to 10⁻¹ m order in terrestrial photogrammetry [23,25,35,38,39,40] or UAV photogrammetry [21,23,24,39,40,41,42]. These last accuracies are comparable with those obtained by means of GNSS or TS surveys [13,19,20].

Following the methodology developed in the studies of [13,19,28,45], a minimum level of detection (minLoD) threshold could be defined from the uncertainties in order to perform the height differences or volumes calculations from DEMs in a reliable way. Therefore, a simple approach could be discarding the values lower to the minLOD defined as the SD or RMS errors. In a normal distribution, these values represent 68% of the confidence interval, so the calculations are free of uncertainty in this percentage. Usually, it is considered twice these errors, which represents 95% of the confidence interval, and so is the accuracy of the calculations. However, height differences and volume calculations are very sensitive to this minLOD [45], and a large amount of information can also be lost with this procedure [13]. Thus, there are other approaches based on the idea that each height difference presents a confidence interval and so a probability of being free of uncertainty can be estimated. From the DoD of each period analyzed, a T-score can be computed and then the probability of being free of a given uncertainty [13]. Finally, the calculations of height differences and volume can be done by weighting each height difference by its probability.

4.2. Areas, Vertical Heights and Volumes in the Whole Area

From the results section, firstly a study area can be observed affected by a gully erosion of variable intensity along the different periods. Qualitatively, Figure 6 shows that depletion or erosion processes (negative height differences) predominate over deposition in the gully area. This is particularly observed in the map of the complete period (Figure 6h) where the gully system extends and branches throughout the whole area.

The area affected by gully erosion is 0.17 km² of a total study area of 7.45 km². Thus, it represents 2.25% of the study area, the gully density being 3.90 km/km². Both are partial data calculated from a gully stretch and an area that does not correspond to a catchment. Meanwhile, the percentage and density data estimated for the entire catchment area of about 20 km² (Arroyo del Cortijo de la Piedra, Figure 1) are 1.35% and 3.15 km/km², respectively. These values are in the same order of magnitude as those found in previous studies for catchment areas of similar extension [49] or even larger [21,24,33,43,53,55]. Nevertheless, some extreme cases have been documented where values between 16% and 60% are reached [15,25,47,56], although the areas considered are so different that the results are hardly comparable.

Within the gully area, in turn, the percentage of depleted area for the whole period of analysis (1980–2016) becomes much larger (31%) than the percentage of depositional area (7%), although the uncertainty area, considered here as the interval between ±1 m (±RMS Z), reaches more than 60% (Table 5). This uncertainty area is not an area where erosion and deposition processes do not occur, as it has been discussed before, and a correction based on the error probability has been applied to the calculation of height differences and volumes. However, discarding the uncertainty area, depletion or erosion predominate over the deposition or accumulation of soil material (63% and 37%, respectively). These results coincide with those observed in some studies [47], unlike other ones relative to fluvial systems where both processes are balanced [13,32] or even the accumulation processes predominate [28].

In the same sense, the balance between the average of depletion (0.61 m) and deposition height differences (0.10 m) in the gully area became 0.51 m of depletion (Table 6). The rates are of 0.017 m/year for depletion, 0.003 m/year for deposition and 0.014 m/year of negative balance, which confirms the predominance of depletion or erosion processes with respect to the deposition or accumulation processes. These heights of decimeter-meter order are comparable to some reference values found in approaches based on aerial photogrammetry and LiDAR [15,28,30,32,45,47,48,78].

In volume, it can be observed that the depletion volumes are generally larger than the deposition volumes, in absolute values, so the negative balance volume for the complete period (1980–1996) is about 85,000 m³ (Table 7) which must be evacuated by the drainage network to which the gullies lead. The rates are 2800 m³/year for depletion and 500 m³/year for deposition, which produces a negative balance (waste) near 2400 m³/year. Considering the whole study area (745 ha) and a bulk density of soils of 1.5 t/m³, the rates are of 5.72 t/ha*year, 0.94 t/ha*year and 4.78 t/ha*year, respectively. These rates are in accordance with the values estimated for the province of Jaén [65], taking into account that these rates are for all erosion processes including laminar, rill and gully erosion. Moreover, they are within the range found in the references [10,11,49], although in their lower values. Nevertheless, this range is very wide depending on the area extension and environment, if the catchment or gully area is considered, or how the measurement is performed (for instance, depletion volume or sediment production). Usually, when very large areas of 10⁶ ha order are considered [10,43], rates around and even lower than 1 t/ha*year are found. When the areas are between 10² and 10⁶ ha, the rates are between 1–10 t/ha*year. Finally, areas smaller than 10² ha present rates higher than 10 t/ha*year [10,11,78]. However, most study areas with similar approaches and extension as those considered in this study present rates much higher, even when the whole catchment is considered: 39.7 t/ha*year [49], 331 t/ha*year [47], between 160 and 430 t/ha*year [48], around 700 t/ha*year [28], 871 t/ha*year [40] and extreme values of 1500–2500 t/ha*year [78]. If only the gully area (16.75 ha) is considered, the rates estimated in our analysis reach values of 255 t/ha*year for depletion, 42 t/ha*year for deposition and 213 t/ha*year for the (negative) balance, more similar to those found in the references.

By periods, the analysis is much richer, as the different periods present great variations regarding the average values for the whole area. Thus, in the maps of Figure 6 intense depletion or erosion processes can be observed in the periods 1996–2001, 2009–2011 and 2011–2013, especially in the last two. Quantitatively, the higher proportion of uncertainty areas corresponds to periods in which the processes are less intense. Discarding the uncertainty areas, the proportion of depletion areas to deposition areas is balanced in the periods 1980–1996, 2001–2005, 2005–2009 and 2013–2016, while it is about twice in the periods 1996–2001, 2009–2011 and 2011–2013, especially in 2009–2011 (Table 6).

This coincides with the higher values of average height differences of depletion (decimeter order), which occurs in the same periods. It is also in accordance with the higher (negative) values of average balance, given that the average deposition values present in general low values in every period (centimeter order). The rates even increase the differences between periods, and therefore the maximum average depletion and balance height differences in absolute terms occur in the period 2009–2011 (values higher than 0.10 m/year), followed by the period 2011–2013 (0.10–0.06 m/year) and the period 1996–2001 (values lower than 0.05 m/year).

Regarding the volumes, the analysis is similar with three periods, 1996–2001, 2009–2011 and 2011–2013, showing depletion and balance (negative) volumes higher than the other periods, while the deposition volumes are usually low (Table 7). Some periods such as the first one (1980–1996) present large absolute volumes, both of depletion and deposition. This is due more to the uncertainties in the models obtained from photographs of a worse quality (digitized original film images) than to real differences between DSMs over a long period of time. The rates show more clearly the different erosion activity in the periods with values for balance rates near to 20,000 m³/year in the period 2009–2011, around 10,000 m³/year in the period 2011–2013 and 5000 m³/year in the period 1996–2001, while in the remaining periods, the rates are insignificant.

The higher erosion activity, regarding the other ones, in the periods 1996–2001, 2009–2011 and 2011–2013 can be related to rainfall (Figure 9). The weekly rainfalls show maximum values (higher than 100 mm) in the autumn-winter of the years 1996–1997, 1997–1998, 1999–2000, 2009–2010, 2010–2011 and 2012–2013. In fact, the absolute maximum value of 150 mm is reached in November 2012 (Figure 9b). Meanwhile, the monthly rainfalls also present maximum values (around 250 mm) in the winter of 1995–1996, 1996–1997, 1997–1998, 2009–2010, 2010–2011 and 2012–2013, reaching the maximum absolute value of 310 mm in January 2010 (Figure 9c). Thus, the maximum erosion activity that occurs in the period 2009–2011 is related to the rainfalls of the autumn–winter of 2009–2010 and 2010–2011, especially the former; the activity of the period 2011–2013 is related to the rainfalls of the autumn-winter of 2012; and the activity of the period 1996–2001 is related to the rainfalls of the autumn-winter of 1996–1997 and 1997–1998. The relationship between rainfall and erosion has been well established in different environments all over the world, rainfall being the most important triggering factor of these erosion processes [49]. In fact, in the Andalusian region the analysis of the evolution of drainage networks from historical orthophotography (1956–2013) shows similar patterns to the results of this study [49]. Thus, the maximum values of precipitation in 24 h and the mean annual rainfalls which occurred in 1997 and 2010 generated an increase of the drainage network. These patterns and relationships have been observed in other processes such as landslides in the region [57,70] under an irregular rainfall regime in which dry periods of several years alternate with wet periods concentrated throughout the autumn-winter seasons of two or three consecutive years.

Nevertheless, as can be observed in Figure 9 and Table 6 and Table 7, the rainfalls related to the period 1996–2001 are approximately 80% of the rainfalls of the period 2009–2011, but their consequences in the erosion processes are about 50%. Thus, some questions about the influence of other factors, in addition to the rainfalls, should be analyzed. Among these the influence of rural trails, paths and roads (as shown in Figure 2c) and changes in land use and practices but also the mechanism of gullies’ growth once the process has started. Although the influence of precipitations and changes in the land use have been analyzed in areas near to the study area of this paper [49], additional data is necessary in order to extract conclusions about the regional influence of all these factors.

4.3. Areas, Vertical Heights and Volumes in the Detailed Area

In general, all the observations made in the previous section for the whole area are valid in the detailed area, but the heights, volumes and rates are different. Thus, the depletion processes are clearly observed in the gully area (Figure 7). The catchment area covers a surface of 30.83 ha and the gully stretch 1.81 ha, which represents a gully intensity of 5.87%, approximately twice the percentage estimated for the whole area.

In the same way, in this sector, the average height difference for depletion in the complete period 1980–2016 is almost three times (1.70 m) the value computed in the whole area (0.61 m). Meanwhile, the average for deposition is practically insignificant and so the average for the balance is practically equal to the depletion (Table 8a). Then the average rates for the depletion and balance height differences reach values of around 0.05 m/year. This means that in this active sector of the gully, the erosion processes predominate absolutely over the deposition processes. This is confirmed by the values shown by the volume analyses (Table 9a). The average depletion and balance volumes are around 30,000 m³, approximately a third of the volume of the gully stretch of the whole study area, while the deposition volumes are practically negligible. The volume rates of depletion and balance reach values near 900 m³/year, which translated to mass rates surpasses 40 t/ha*year. These values are significantly higher than the values calculated for the study area and in the middle range of those found in the province and the references [10,11,49]. If only the gully areas are considered, the rates become near to 700 t/ha*year, comparable with some extreme values of the references [28,40,47,78].

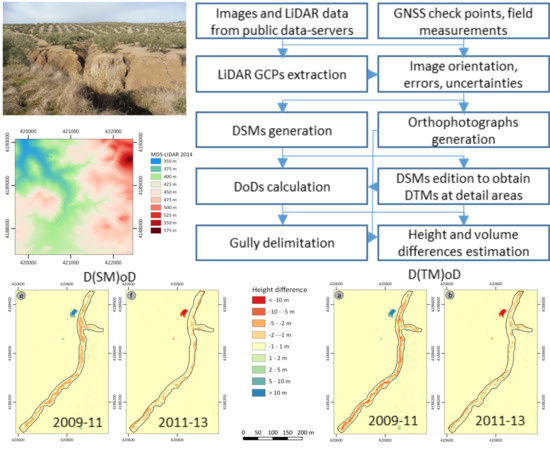
As for the whole area, there are periods in the detailed sector with significantly higher values, such as the periods 2009–2011 and 2011–2013. This can be observed in the maps of Figure 7 (especially in Figure 7e,f), where the negative values of the height differences (depletion) reached in the gully areas in these periods predominate over the null or positive values (deposition). Moreover, the resolution of these figures allows us to observe the distribution of the depletion areas that in the period 2009–2011 were concentrated in the center or axis of the gully, while in the period 2011–2013 they were displaced towards the lateral walls of the gully. This led to an evolution first by means of vertical incision (2009–2011) and later by means of gully wall retraction. Quantitatively, these periods present notable rates of depletion and balance height differences (0.50 m/year and 0.30 m/year) regarding the remaining periods in which the rates are insignificant (Table 8a). Even in the period 1996–2001, when rates in the whole area reach a remarkable level, in this particular area, they are practically negligible. The volume analysis is even clearer (Figure 9a), since the depletion and balance rates of these periods are higher in an order of magnitude (8000 m³/year and 5000 m³/year) than the other ones (always under 800 m³/year). The translation of these volumes to mass rates allows extreme values to be reached, up to 275–425 t/ha*year for balance, as those found in the references [28,40,47].

The relationship of the erosional activity in this area to rainfalls leads to similar conclusions as those for the whole area. Thus, the maximum values both in the weekly and monthly rainfalls in the periods 2009–2011 and 2011–2013 are related to the higher erosion and loss of soils in these periods (Figure 9). However, the notable activity of the period 1996–2001 in the whole area, related to the rainy years 1996–1998, is not found here. This leads us to consider the influence of local triggering factors such as the roads and rural ways and land use and practices that accelerate or inhibit the erosion processes. Regional studies of determinant and triggering factors as well as hazard analysis, which exceed the objective of this study, could lead to a greater knowledge about the causes and evolution of erosion processes in the region.

Regarding the influence of DEMs resolution and data processing, some tests were performed. First, only manual edition to obtain DTMs from DSMs did not produce a significant improvement in the models and calculations, and the increase of resolution (until 1 m) did not either. Meanwhile, the combination of the edition procedure with the introduction of break lines at a resolution of 1 m (Figure 8) allowed the significant improvement of the DTMs definition. Thus, when processing DTMs of the period 2009–2011 (edited and interpolated with break lines), the rates of depletion and balance height differences increase by 50% (from 0.50 m/year to 0.75 m/year, Table 8b). However, these rates do not change in the period 2011–2013 (0.33 m/year). Meanwhile, the rates for depletion and balance volume also increase, in this case by 40% (from 10,000 m³/year to 13,500 m³/year) for the period 2009–2011, but they do not change either in the period 2011–2013 (Table 9b).

From these data, first a subestimation of the intensity of the erosion processes is observed when only the DSMs are considered and linear interpolation is applied to obtain the models. Thus, the depletion heights and volumes can become 40%–50% higher if the DSMs are edited and break lines are considered in the interpolation, as in the period 2009–2011. This sub-estimation should be taken into account in the quantification of gully erosion in addition to the uncertainties derived from the orientation processes. However, this behavior is not observed in all cases, such as in the period 2011–2013 in which the heights differences, volumes and rates are similar in both edited and non-edited models. These differences in the behavior of the DTMs after edition could be related to the shape of the gully section and thus to the erosion processes involved. Thus, from the observation of profiles or sections of DSMs and DTMs, the DoDs and the orthophotographs (Figure 10), it is observed that the gully growth in depth until the period 2009–2011 is mainly in the vertical component (gully incision). In this case, the resulting shape of the 2011 section is very steep and narrow. This is in accordance with the observation of the height difference map of this period (Figure 7e and Figure 8a), which is higher in the gully central axe. Therefore, in these steep section, shapes linear interpolation can smooth the model and sub-estimate the depth and thus the height differences and the volumes. However, the growth of the gully in the period 2011–2013 is mainly in the horizontal component by lateral walls retraction more than the incision. This leads to a wider and less steep section, where the interpolation does not smooth so much the models, and thus, the differences between the DSMs without break lines and the edited DTMs with break lines are practically insignificant. It also confirms the evolution observed in the height difference maps (Figure 7f and Figure 8b), where the height differences are displaced from the gully central axe to the lateral walls.

Despite the observed sub-estimation of height differences and volumes in some given gully morphologies, the technique applied with automatically generated DSMs is very useful for a first identification and even quantification of gully processes. If more accurate measurements are needed, a model edition is required in some cases. It means the application of time-consuming procedures, which are not always justified for large areas. In any case, the availability of more quality models such as LiDAR datasets and those coming from aerial or UAV surveys of very high resolution and quality would contribute to reducing the errors and uncertainties of models.

The analysis of the sections obtained in 2009, 2011 and 2013 allows the estimation of gully depths. Thus, considering the DTMs in this point of the gully system where the erosion processes are very intense, the depth is about 1.3 m in 2009, about 5.5 m in 2011 and almost 6.0 m in 2013.

5. Conclusions

The usefulness of geomatics techniques, mainly photogrammetry and LiDAR, for the study of superficial processes like gully erosion and landslides is proved again with success. The accuracy and consistency of these techniques enables the detection of change in detailed terrain features over long periods and large areas.

The methodology developed in this study is based on the extraction of GCPs from LiDAR data that allows the orientation of historical flights in a common coordinate reference system, avoiding or reducing the field GNSS measurements of the GCPs. Then, DMS, DoDs and orthophotographs are obtained and analyzed. In this study all data, both the different images and the LiDAR point cloud, are public and available from different spatial data infrastructures and database servers. This approach allows these studies to be addressed without the necessity for data capture, which is a costly process in time and money.

Regarding the accuracy of the methodology, the propagated RMS error estimated for the LiDAR data and the image orientation process is about 0.80–0.90 m for the horizontal (XY) component and 0.50–0.95 m for the vertical (Z) component. These propagated errors for the vertical (Z) component lead to consider the uncertainties of DSM of Differences (DoDs) of about ±1 m. Such uncertainties are enough to identify and map gully erosion processes and to quantify them through the calculation of height differences and volumes between successive digital elevation models.

The gully area, delimitated from the interpretation of DoDs and orthophotographs, is of 0.17 km², which represents 2.25% of the whole study area. The height differences present an average balance of 0.51 m for the gully area in the complete period, with maximum average rates of depletion around 0.10 m/year in some periods such as 2009–2011 and 2011–2013. Meanwhile, the waste volume in the complete period is about 85,000 m³, reaching maximum rates of 10,000–20,000 m³/year. It produces mass rates of 20–40 t/ha*year in the periods of higher activity, considering the total study area (745 ha) and a soil density of 1.5 t/m³. This different activity of the erosion processes over time can be related to the rainfall regime. Thus, the weekly and monthly rainfalls reach maximum values higher than 100 and 250 mm, respectively, in some episodes included in the periods 1996–2001, 2009–2011 and 2011–2013. These coincide with the periods of highest activity of the erosion processes. The relative lower erosion activity in the rainy period 1996–2001 with respect to 2009–2011 and 2011–2103 leads to further analysis of the influence of other factors. For instance, the presence or the construction of new rural ways and roads, changes in the land use and practices and the mechanisms of gullies’ growth, in addition to the rainfall, should be analyzed when additional data are available. The analysis performed in the detailed area confirms these data and the relationships with triggering factors. The average for the balance difference heights in the complete period is 1.70 m of depletion, with maximum rates of 0.30–0.50 m/year in the periods 2009–2011 and 2011–2013. The balance volumes are around 30,000 m³ for the complete period, reaching values between 5000–8000 m³/year (275–425 t/ha*year) in the periods 2009–2011 and 2011–2013.

The analysis of DTMs, obtained by the manual edition of some DSMs in the detailed area, allows us to extract some ideas about the approach implemented, mainly related to the models’ resolution and the shape of the gully. Thus, given that there are no significant changes when only manual edition is considered (even increasing the resolution from 2.5 m to 1 m), this leads to the necessity of adding break lines to the interpolation. When these features are included the depletion heights and volumes increase by 40%–50%. Hence an underestimation of erosion processes can occur if only automatic model generation is applied. However, this behavior is observed mainly in models corresponding to gullies with steep and narrow sections (2011), but not in those gullies with smoother sections (2013).

Future advances in the methodology can lead to a greater automation of the point (GCPs) extraction and measurement from LiDAR data, as well as the creation of routines to generate DEMs and DODs, to calculate height differences and volumes and to make gully maps in a GIS environment. Further approaches to the automatic edition of models in order to obtain true DTMs, including the using of new LiDAR datasets, will be also addressed. Indeed, these procedures will contribute to apply this methodology to larger extensions in a more efficient way. Moreover, the analysis of a larger extension of gullies with different shapes and properties and, in addition, factor analysis based on classical statistical or modern machine learning techniques will permit a deeper knowledge of the dynamics of erosion processes in the study area.