A Convolutional Neural Network and Matrix Factorization-Based Travel Location Recommendation Method Using Community-Contributed Geotagged Photos

Abstract

Travel location recommendation methods using community-contributed geotagged photos are based on past check-ins. Therefore, these methods cannot effectively work for new travel locations, i.e., they suffer from the travel location cold start problem. In this study, we propose a convolutional neural network and matrix factorization-based travel location recommendation method to address the problem. Specifically, a weighted matrix factorization method is used to obtain the latent factor representations of travel locations. The latent factor representation for a new travel location is estimated from its photos by using a convolutional neural network. Experimental results on a Flickr dataset demonstrate that the proposed method can provide better recommendations than existing methods.

1. Introduction

The continued growth of photo-sharing sites (e.g., Flickr and Panoramio) has increased the volume of community-contributed geotagged photos (CCGPs) that are available on the Web. These large amounts of CCGPs include rich information (e.g., user-provided tags, time, and visual contents, as shown in Figure 1 and

Table 1. Sample metadata of CCGPs; a few attributes are not shown.

Photo ID	User ID	Tags	Date Taken	Latitude	Longitude
pic00139703	user0001435	France, Paris, honeymoon, Eiffel tower	2006-03-26 01:33:10	48.873747	2.324981
pic00054003	user000908	England, London, Thames, Tower bridge	2006-05-05 18:05:55	51.50942	0.107266

). This information is tremendously useful for travel location recommendation systems [1], taking into consideration users’ travel preferences depending on their past check-ins, and developing travel location recommendation systems.

CCGPs usually include metadata, e.g., social relation, textual and contextual attributes [2,3,4,5]. Collaborative filtering (CF) is widely used by CCGP-based travel location recommendation methods, which are based on the simple conjecture of recommending a travel location to the user if similar users have interactions with the travel location [6,7]. Due to its simplicity, scalability, and flexibility, matrix factorization, which is a popular CF method that learns a latent factor to represent interaction ratings, becomes a widely used model for travel location recommendation [8,9]. Ratings in the user–travel location interaction are explicit information, which has been deeply exploited in early travel location recommendation methods. To address sparse ratings, auxiliary attributes, e.g., contextual and textual attributes [10,11], are integrated into matrix factorization. However, existing integrated methods only work on implicit/explicit rating prediction problems, and latent factor representation is not learned effectively with highly sparse content information. Therefore, these methods cannot fully capture travel location information and recommend a travel location without any past check-ins, i.e., the travel location cold start problem [12,13,14].

Recently, convolutional neural networks (CNN)s of powerful representation learning abilities shows high performance in different domains, e.g., signal processing [15] and natural language processing [16]. CNN effectively catches local features from different layers and transforms features to a single vector [17]. Therefore, CNN can be used to estimate the latent factor representations of new travel locations by providing comprehensive understanding of photos.

To address the above-mentioned problem, i.e., we cannot obtain the latent factor of a travel location from past check-ins; we propose to use a CNN to estimate the latent factor of a new travel location from its photos. We seamlessly integrate CNN into weighted matrix factorization (WMF), which is commonly used to recommend travel locations. In addition, we use similarity weight between users (and travel locations) to exploit auxiliary attributes, which are integrated into the WMF process to recommend travel locations. To the best of our knowledge, our work is the first to study the location cold start problem of travel location recommendation using photos. The main contributions of this study are summarized as follows.

• Propose a CNNMF method that integrates CNN and WMF. If a travel location does not have any past check-ins, the method uses a CNN to estimate its latent factor representation from its photos.
• Employ similarity weights between users (and travel locations) to exploit contextual attributes (i.e., time, weather, and season), textual attributes (i.e., tags), and geographical attributes (i.e., distance).
• Evaluate the proposed method on a CCGPs dataset that covers nine popular cities worldwide. Experimental results show that CNNMF can effectively address the travel location cold start problem and achieve competitive recommendation performance.

The remainder of the paper is organized as follows: Section 2 presents the related work. Section 3 presents the basic concepts and defines the problem. Section 4 introduces the motivation and design of the methodology. Section 5 presents the experiments. Section 6 concludes the paper and provides some future work recommendations.

2. Related Work

In this section, we survey some recent work related to our study, which contains: (1) CCGP-based travel location recommendations and (2) using extra data to address the location cold start problem.

2.1. CCGP-Based Travel Location Recommendation

CCGP-based travel location recommendation methods focus on two types of recommendation: general and personalized travel location recommendations. Methods of general travel location recommendation focus on recommending popular travel locations and sequences, which usually extract and cluster travel locations and sequences from past check-ins. Jiang et al. [18] proposed obtaining travel sequences from CCGPs by taking multiple attributes (e.g., time, cost, and tags) into account. Liu et al. [19] used a generative method and convolutions network to model users’ check-in sequences. Other typical methods have been used to recommend locations and sequences in a given geospatial area [20,21]. Zheng et al. [20] analyzed the relationship between tourists’ patterns and the regions of attraction. Chen et al. [21] fused geotagged photos and check-ins for route recommendation.

By contrast, methods of personalized travel location recommendation focus on recommending travel locations that are suitable for users’ preferences. Majid et al. [1,22] proposed recommending travel locations by using users’ preferences in past check-ins using different contexts (e.g., time and weather). In recent years, user attributes (e.g., age and gender) have been extracted from photo contents to construct user profiles [23,24]. Cheng et al. [23] extracted user attributes from photo contents, which was extended to include travel group type (e.g., couples, friends, and families) [24], and evolution continued by integrating the above-mentioned attributes with matrix factorization for travel location recommendation [9]. These methods are alternative ways to relieve the limitations of metadata by obtaining users’ travel preferences from the contents of CCGPs (e.g., users’ age and gender information), which cannot effectively work to mitigate the travel location cold start problem.

2.2. Using Extra Data to Address the Travel Location Cold Start Problem

Researchers have also focused on relieving the travel location cold start problem. Gao et al. [12,13] incorporated social network information with geo-social correlation to capture geographical distance and social network from location-based social networks to mitigate the problem. Sun et al. [3] proposed the integration of context information with a support vector machine to solve the regression problem. The main purpose is to extract more attributes to address the problem. However, few studies have investigated the travel location cold start problem. Despite their effectiveness for various data mining tasks, photo contents have not been studied for mitigating the problem.

Many studies have been conducted on using photo contents to extract travel location information, which is based on color, texture, or shape representation [25,26,27]. Ke et al. [25] proposed a method that transforms the photo annotation problem into a multi-label learning problem. Kuang et al. [26] estimated visual information from photos by associated tags in a local region. Xing et al. [27] extracted features from photos to obtain users’ preferences and travel location properties. Weyand et al. [28] determined where a photo was taken only from its pixels by dividing the surface of the earth into thousands of multi-scale geographical cells. Wang et al. [29] proposed a method to extract visual contents from photos to help learn of latent factor representations; the probability method for learning fails to obtain accurate travel locations from hidden features. The reason is that each travel location has limited photos, which are insufficient to describe the travel location.

Our method is different from the above-mentioned methods. We use a CNN to estimate the latent factor of a new travel location from its photos. Latent factors obtained by applying WMF to the past check-ins are used as ground truths to train the CNN.

3. Preliminaries and Problem Definition

The following definitions of certain basic concepts and terms are given to formalize our method.

Definition 1

(Geotagged photo).A geotagged photo indicates the travel location embedded in the photo and can be defined as tuple$h=\left(id,u,cord,t\right)$. Each photo contains a unique identification$id$and coordinate$cord$, which is tagged by the user$u$at time$t$.

Definition 2

(Check-in).A user–travel location interaction is represented as a tuple$\beta =\left(u,l,t\right)$, which means user$u$visits travel location$l$at time$t$.

Definition 3

(Travel location).A travel location$l$is a specific geographic place that a user can visit and take photos.

Definition 4

(Photo collection).A collection of photos taken by all the users is represented as a set, where is the collection of photos taken by user$u_n$.

Definition 5

(New travel location representation).A new travel location latent factor is estimated from its photos by using CNN architecture as a function that takes a raw photo as input, while the output is latent vectors of each photo defined as a tuple$l_j^{\prime }=CNN\left(W,r_j\right)$, where$W$represents all the weight and bias variables, and$r_j$denotes the photo raw feature vector of travel location$j$.

Our research problem can be formulated as follows. If a travel location does not have past check-ins, then CNNMF uses a CNN to estimate its latent factor representation from its photos, and seamlessly integrates CNN into WMF, from which we aim to recommend new travel locations to users.

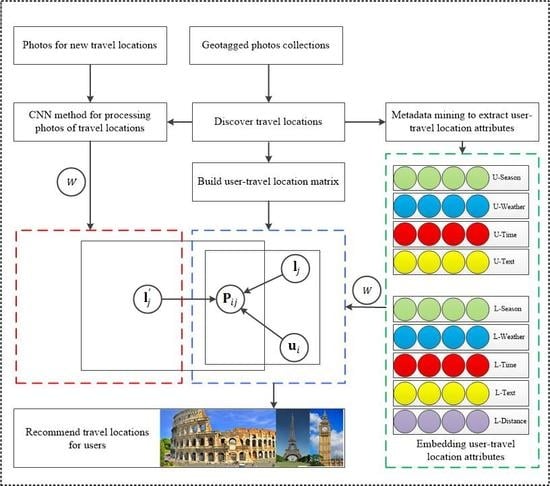
4. Methodology

The framework of CNNMF is illustrated in Figure 2. The travel locations are determined using the spatial proximity of CCGPs. Then, from the visited travel locations, we build the interaction user–travel location matrix. Heterogeneous metadata are mined to exploit contextual attributes (i.e., time, weather, and season), textual attributes (i.e., tags), and geographical attributes (i.e., distance), which are incorporated into the WMF process to recommend travel locations. We also use a CNN to process the content of photos for estimating latent factors in travel location cold start cases.

4.1. Discovering Travel Locations from CCGPs

Discovering travel locations from CCGPs can be considered a clustering problem. Clustering algorithms, such as mean-shift, have been applied to discover travel locations from CCGPs [30]. The DBSCAN [31] algorithm has the following advantages compared with other clustering algorithms: (1) it requires minimum domain knowledge to determine parameters and identifies clusters with spot style; (2) it can work efficiently with large-scale data. However, the DBSCAN algorithm is unsuitable for extracting travel locations from CCGPs because of the different sizes and densities. To address this problem, Kisilevich et al. [32] presented a new clustering algorithm based on DBSCAN called P-DBSCAN, which is suitable for checking the place and event using a combination of CCGPs and can provide the definition of direct density reachable by utilizing adaptive density.

In our study, the P-DBSCAN clustering algorithm is used to find travel locations from CCGPs. We obtain a set of travel locations $L=\left\{l_1,l_2,\dots ,l_n\right\}$. Each location element is defined as $l$ = {${\mathcal{P}}_l,cor{d}_l$}, where ${\mathcal{P}}_l$ is a collection of clustered photos and $cor{d}_l$ at the geographical coordinates appears centroid of CCGPs.

4.2. Obtaining Explicit Information

4.2.1. Contextual Information Modeling

Time-stamp information allows the recovery of weather context $w$, creating a time of day context $t$, and gets the season context $s$. Weather web services (WWSs) normally provide us the information related to weather status at the hourly, daily, or monthly foundation. By using WWSs with a time-stamp, we can discover context w (including temperature and sky condition) when visit $\beta =\left(u,l,t\right)$ is made. We use the API of wunderground.com to obtain weather information. To obtain context $t$, we exploit the mean taken time of the photos belonging to a visit. Context $s$ is then derived. The detailed definitions about time of day, season, and weather contexts are as follows:

• Time of day: weekday AM, weekday PM, weekend AM, and weekend PM.
• Season: spring (Mar-Apr-May), summer (Jun-Jul-Aug), autumn (Sept-Oct-Nov), and winter (Dec-Jan-Feb).
• Weather-temperature: hot (≥25 °C), warm (15–25 °C), cool (5–15 °C), and cold (<5 °C).
• Weather-sky condition: sunny, cloudy, rainy, snowy, and foggy.

4.2.2. Textual Information Modeling

The metadata of CCGPs have rich heterogeneous information (e.g., textual information). Tags are classified under textual information, which is necessary for modeling users and travel locations [7,33]. The topic model, e.g., latent Dirichlet allocation (LDA) [34], assumes each document is a collection (corpus) that can be described as a mixture of topics, where each topic is defined by a collection of “typical” or “likely” words. The graphical model representation of the LDA model is presented in Figure 3, which works as follows:

• Select parameters ${\mathsf{\theta }}_i$-𝐷𝑖r ($\mathsf{\alpha }$), where ${\mathsf{\theta }}_i$ is the topic distribution of document $i$ and 𝐷𝑖r ($\mathsf{\alpha }$) is the Dirichlet distribution of parameter 𝛼.
• For each word:
  • Select a topic $z$-multinomial (${\mathsf{\theta }}_i$).
  • Select a word $w$-multinomial (${\mathsf{\beta }}_z$).

Our method uses the topic model to gain the latent topic spread of users and travel locations for addressing the textual information of CCGPs. The tag set of all the photos of a travel location $l$, as well as that of a user $u$, is regarded as a document, and we use the topic model to obtain the topic distribution $tx{t}_l$ and $tx{t}_u$.

4.3. Obtaining Explicit Information

After explicit attributes are obtained, user and travel location features are constructed as $u=\left(w_u,s_u,t_u,tx{t}_u\right)$ and $l=\left(w_l,s_l,t_l,tx{t}_l,di{s}_l\right)$. The combination of the user and travel location features are applied in matrix factorization. $M_{ll}$ represents the similarity matrix between two travel locations, and $M_{uu}$ represents the similarity matrix between two users. Both $M_{ll}$ and $M_{uu}$ are utilized to help the factorization of user–travel location matrix. A similarity value is between 0 and 1, and a large value indicates high similarity. $dis\left(l_j,l_k\right)$ is the geographical distance between two travel locations. Travel location–travel location similarity can be calculated by Equation (1):

$${\mathrm{Sim}}_l\left(l_j,l_k\right)=\frac{{{\displaystyle \sum }}_{q=1}^y{x}_{jq}\times x_{kq}}{\sqrt{{{\displaystyle \sum }}_{q=1}^y{x}_{jq}^2}·\sqrt{{{\displaystyle \sum }}_{q=1}^y{x}_{kq}^2}},$$

(1)

where $x_{jq}$ and $x_{kq}$ represent the $q^{th}$ feature of travel locations $l_j$ and $l_k$, respectively. $y$ is the number of features. User–user similarity can be calculated by Equation (2):

$${\mathrm{Sim}}_u\left(u_i,u_k\right)=\frac{{{\displaystyle \sum }}_{g=1}^{y^{\prime }}{x}_{ig}\times x_{kg}}{\sqrt{{{\displaystyle \sum }}_{g=1}^{y^{\prime }}{x}_{ig}^2}·\sqrt{{{\displaystyle \sum }}_{g=1}^{y^{\prime }}{x}_{kg}^2}},$$

(2)

where $x_{ig}$ and $x_{kg}$. represent the $g^{th}$ feature of users $u_i$ and $u_k$, respectively. $y^{\prime }$. is the number of features. Weighted travel locations and users similarities can be calculated by Equations (3) and (4), respectively.

$${\mathrm{Sim}}_l\left(l_j,l_k\right)=a\times si{m}_l\left(l_j,l_k\right)+b\times \frac{1}{1+dis\left(l_j,l_k\right)},$$

(3)

$${\mathrm{Sim}}_u\left(u_i,u_k\right)=c\times si{m}_u\left(u_i,u_k\right),$$

(4)

where $a,$ and $b,$. represent similarity weight between travel locations and $c$ represents similarity weight between users, which are used to help the factorization of user–travel location interaction. The weights are set as follows: $\mathrm{a}=\mathrm{b}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ and $\mathrm{c}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$.

4.4. Factorizing User–Travel Location Interaction

The user–travel location interaction plays an important role in the context of travel location recommendation. Let $r_{ij}$ be the number of times that user $i$ has visited travel location $j$, which can be obtained from the past check-ins. To calculate the weighted effect of user and travel location, we use the WMF algorithm [35]. Let $P_{ij}$ be the preference of user $i$ to travel location $j$, which is obtained by binarizing $r_{ij}$, as shown in Equation (5). Let $C_{ij}$ be the confidence of $P_{ij}$, which is obtained by Equation (6).

$$P_{ij}=\{\begin{array}{c}1r_{ij}>0\\ 0r_{ij}=0\end{array}$$

(5)

$$C_{ij}=1+\gamma \log \left(1+{ϵ}^{-1}{r}_{ij}\right),$$

(6)

where $\gamma$ and $ϵ$ are hyper parameters. Suppose that $u_i\in {ℝ}^{N\times k}$ be the users latent preferences, $l_j\in {ℝ}^{M\times k}$ be the travel locations latent properties. The basic travel location recommendation method approximates ${u_i}^{\prime }s$ latent preferences in an unvisited $l_j$ by solving the following optimization problem.

$$\underset{u_{\ast ,}{l}_{\ast }}{\min }\frac{1}{2}{\displaystyle \sum }_{i,j}{C}_{ij}{\left(P_{ij}-u_i^T{l}_j\right)}^2,$$

(7)

where $C_{ij}\in {ℝ}^{N\times M}$ is the check-in weighting matrix with $C_{ij}=1$ indicating that $u_i$ has checked in at $l_j$, $C_{ij}=0$ otherwise. Following a previous work [9], the heterogeneous similarity information introduces user–user similarity and travel location–travel location similarity can be used to constrain a WMF for travel location recommendation, which is presented in Equation (8):

$$\begin{gathered} \underset{u_{\ast ,}{l}_{\ast }}{\min }\frac{1}{2}{\displaystyle \sum }_{i,j}{C}_{ij}{\left(P_{ij}-u_i^T{l}_j\right)}^2+\frac{{\lambda }_1}{2}\left({\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{g\in G\left(i\right)}si{m}_u\left(i,k\right)\Vert u_i-u_k\Vert {}_F^2+{\displaystyle \sum }_{j=1}^n{\displaystyle \sum }_{q\in Q\left(j\right)}si{m}_l\left(j,k\right)\Vert l_j-l_k\Vert {}_F^2\right) \\ +\frac{{\lambda }_2}{2}\left(\Vert u_i\Vert {}_F^2+\Vert l_j\Vert {}_F^2\right), \end{gathered}$$

(8)

where $u_i$ is the latent factor vector of user $i$, and $l_j$ is the latent factor vector of travel location $j$, the two regularization terms $\Vert u_i\Vert {}_F^2$ and $\Vert l_j\Vert {}_F^2$ are used to avoid overfitting, and $G\left(i\right)$ and $Q\left(j\right)$ are the user and travel location similarities of user $i$ and travel location $j$, respectively. ${\lambda }_1$ and ${\lambda }_2$ are nonnegative parameters used to control the regularization terms and the similarity of regularization terms.

4.5. Exploiting Visual Content

With powerful representation learning abilities, CNN is widely used to improve the state-of-the-art, e.g., signal processing [15] and natural language processing [16]. CNN can effectively catch local features from different layers and transform features to a single vector [17]. We select the state-of-the-art CNN architecture VGG-16 [36], which consists of 16 layers, including 13 convolution, 3 fully connected (FC), 5 max-pooling, and 1 softmax layer, as shown in Figure 4. The size of the input photo is $224\times 224\times 3$, where $3$ is the number of channels (i.e., RGB), and each CCGP is resized to $224\times 224$. Recent transfer learning studies have demonstrated that CNN trained on one large dataset can be generalized to extract CNN features for other datasets, and outperform the state-of-the-art approaches on these new datasets for different tasks [37,38]. Therefore, we use pre-trained to initialize the weights of VGG-16 on the place database. Let $f_l$ index the $l^{th}$ convolutional layer, $v_l$ the number of filters in the $l^{th}$ convolution layer, $z_l$ be the spatial size of the filter, and $m_l$ be the spatial size of the output feature map. The updating of $W$ is dominated by the computation of the convolution layer, and the time complexity for one input cost is $O\left(f_l{z}_l^2{v}_l{m}_l^2\right)$ [39]. We remove the last FC and softmax layers, which are used for classification purposes, and take the output of the second FC layer (i.e., FC7) as the representation of a CCGP, i.e.,$r_j$.

4.6. Estimating Latent Factor from Photos

Estimating latent factors for a given travel location from the corresponding CCGPs is a regression problem. Since latent factors are real-valued, the core objective is to minimize the mean square error of the estimations. Let $l_j$ be the latent factor vector of location $j$, which is obtained by WMF, and $l_j^{\prime }$ is the corresponding prediction by CNN. Then, the minimization problem is presented as follows:

$$\underset{\theta }{\min }{\displaystyle \sum }_j\Vert l_j-l_j^{\prime }\Vert {}^2.$$

(9)

4.7. Travel Location Recommendation

The framework representation of CNNMF is shown in Figure 2. By fusing Equation (8) and Equation (9), the objective function of CNNMF can be written as follows:

$$\begin{gathered} \underset{u_{\ast ,}{l}_{\ast },l_{\ast }^{\text{'}}}{\min }\frac{1}{2}{\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{j=1}^n{C}_{ij}{\left(P_{ij}-u_i^T{l}_j\right)}^2+\frac{{\lambda }_1}{2}\left({\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{g\in G\left(i\right)}si{m}_u\left(i,k\right)\Vert u_i-u_k\Vert {}_F^2+{\displaystyle \sum }_{j=1}^n{\displaystyle \sum }_{q\in Q\left(j\right)}si{m}_l\left(j,k\right)\Vert l_j-l_k\Vert {}_F^2\right) \\ +\frac{{\lambda }_3}{2}\left({\displaystyle \sum }_j\Vert l_j-l_j^{\text{'}}\Vert {}_F^2\right)+\frac{{\lambda }_2}{2}\left(\Vert u_i\Vert {}_F^2+\Vert l_j\Vert {}_F^2\right)+\frac{{\lambda }_4}{2}\left(\Vert l_j^{\text{'}}\Vert {}_F^2\right) , \end{gathered}$$

(10)

where ${\lambda }_3$ and ${\lambda }_4$ are parameters used to control the estimation of latent factor and regularization terms. Equations (11) to (13), which are based on gradient descent, are used to update user $u_i$ and travel location $l_j$, respectively.

$$u_i\leftarrow u_i+\alpha \left(\left(P_{ij}-u_i^T{l}_j\right)l_j-{\lambda }_1{\displaystyle \sum }_{g\in G\left(i\right)}si{m}_u\left(i,k\right)\left(u_i-u_k\right)-{\lambda }_2{u}_i\right)$$

(11)

$$l_j\leftarrow l_j+\alpha \left(\left(P_{ij}-u_i^T{l}_j\right)u_i-{\lambda }_1{\displaystyle \sum }_{q\in Q\left(j\right)}si{m}_l\left(j,k\right)\left(l_j-l_k\right)+{\lambda }_3{\displaystyle \sum }_j\left(l_j-l_j^{\prime }\right)l_j^{\prime }-{\lambda }_2{l}_j\right)$$

(12)

$$l_j^{\prime }\leftarrow l_j^{\prime }+\alpha \left({\lambda }_3{\displaystyle \sum }_j\left(l_j-l_j^{\prime }\right)l_j-{\lambda }_4{l}_j^{\prime }\right)$$

(13)

4.8. The Learning Algorithm of CNNMF

With the above-mentioned update rules, the algorithm of CNNMF is summarized in Algorithm 1. The proposed CNNMF framework uses similarity weight between users (and travel locations) to exploit auxiliary attributes, which are integrated into the WMF process to recommend travel locations. For a new travel location, we initialize the weights of VGG16 by the pre-trained weights on the place database for photo classification. The place database is a very large photo dataset containing 7,076,580 photos from 476 scene categories. This is demonstrated by initializing CNN using pre-trained weights on place database. In practice, we keep the earlier layers fixed. This is motivated by the observation that the earlier features of a CNN contain more generic features that should be useful to many tasks, but later layers of the CNN become progressively more specific to the details of the original dataset and should be useful for travel location recommendation. In summary, all user and travel location latent factors are updated in $O\left(k^2{n}_P+k^{3}N+k^{3}M\right)$ where $n_P$ is the number of observed ratings. Note that photo latent vectors are computed while updating $W$. Time complexity for updating $W$ is dominated by the computation of the convolution layer, and thus all weight and bias variables of CNN are updated in $O\left({\displaystyle \sum }_l^d{v}_{l-1}.z_l^2.v_l.m_l^2\right)$ [39]. The total time complexity per epoch is $O_{WMF}\left(k^2{n}_P+k^{3}N+k^{3}M\right)+O_{CNN}\left({\displaystyle \sum }_l^d{v}_{l-1}.z_l^2.v_l.m_l^2\right)$, and this optimization process scales linearly with the size of the given data. Finally, we compute the score $u_i^T{l}_j$, and recommend the travel locations with the highest scores.

Algorithm 1. The proposed Framework CNNMF

Input: P, user–travel location preference matrix Simu(ui, uk): user–user similarities Siml(lj,lk):travel location–travel location similarities $𝒫$lj for lj ∈ $ℒ$ Output: Latent factor vector of user and travel location ui, lj; 1: initialize the weight of VGG-16 on the place database 2: initialize ui, lj and $l_j^{\prime }$ 3: for each ui do 4:    update by Equation (10) 5: end for 6: for each lj do 7:    update by Equation (11) 8: end for 9:    If travel location j is new then 10:  estimate $l_j^{\prime }$ by CNN(W,fj) 11:  update by Equation (12) 12:  end if 13: return the top travel locations by Pij

5. Experiments

In this section, we are setting experiments to evaluate the performance of the proposed method. We begin by introducing the dataset, parameter settings, the impact of topic number, and the impact of diverse types of information, followed by comparing the proposed method with the state-of-the-art travel location recommendation methods.

5.1. Dataset

We employ the CCGP dataset $\mathcal{D}$ used by Jiang et al. [18], which contains uploads from $7387$ users. The dataset consists of photo albums associated with past check-ins, which are taken in nine popular tour cities (i.e., New York, Los Angeles, Chicago, Barcelona, Berlin, London, Paris, Rome, and San Francisco). We removed photos without latitude and longitude, as well as “selfie photos”, as these photos cannot give enough information about travel locations. The final statistics of the dataset are shown in

Table 2. Sample metadata of CCGPs; a few attributes are not given.

Cities	Users	Travel Locations	Check-in	Photos
				(Filtered)	(Row)
Barcelona	122	37	289	5853	15,704
Berlin	100	36	273	11,083	13,420
Chicago	134	64	416	12,304	22,104
London	270	82	1468	14,256	43,557
Los Angeles	101	30	65	3961	10,122
New York	228	71	782	12,049	34,374
Paris	273	67	1120	10,879	24,507
Rome	125	30	309	7828	18,416
San Francisco	175	56	842	10,060	24,572
Total	1528	473	5564	88,273	206,776

, and the spatial distribution of photos in popular tour cities is shown in Figure 5.

5.2. Parameter Settings

In this section, we provide the setting of several parameters utilized in our experiments.

• To enable P-DBSCAN to detect travel locations from CCGPs, we set a $MinUsers=50$, radius $\epsilon \left(epsilon\right)=100$ m, and density ratio $\omega =0.5$.
• To obtain the user–travel location interaction information, we empirically set a threshold of visit duration $visi{t}_{thr}=6$ h.
• In all the following experiments based on matrix factorization methods, we set parameters ${\lambda }_1=0.01$, ${\lambda }_2=0.1$, ${\lambda }_3=0.001$, ${\lambda }_4=1$, and $\alpha =0.5$.
• CNN is employed to estimate the latent factors of new travel locations. The learning rate parameter is $0.001$ for $60$ epochs and mini-batch size is 128. The momentum is 0.9. The weight decay is 0.0005. The weights are randomly initialized following previous work [40].

In the following experiments, according to visiting time, we split the dataset $\mathcal{D}$ into the training set ${\mathcal{D}}_{train}$ (80%) and the test set ${\mathcal{D}}_{test}$ (20%). Then, use evaluation metrics, i.e., MAP@n and AP@n, were adopted to evaluate the recommendation effectiveness by calculated Equations (13) and (14), respectively.

$$\mathrm{AP}@n=\frac{\left({{\displaystyle \sum }}_{i=1}^n({{\displaystyle \sum }}_{j=1}^{i}li{k}_j)/i\right)}{n},$$

(14)

$$\mathrm{MAP}@n\frac{\left({{\displaystyle \sum }}_{i=1}^{m}A{P}_i\right)}{m},$$

(15)

where $n$ indicates the number of recommended travel locations, and $m$ represents the number of users. The relevance value $li{k}_j=1$ if the user has visited the travel location; otherwise, $li{k}_j=0$.

5.3. The Impact of Topic Number

The number of topics $k$ is a significant parameter and has an impact on recommendation performance. To decide on an optimal number of topics, we conduct an experiment to study its impact. The result is shown in Figure 6, from which we can find that the MAP is up to $30.7\%$ when $k$ is $9$. Thereby, $k$ was set to 9 in the following experiments.

5.4. The Impact of Diverse Types of Information

To explore the impact of diverse types of information on travel location recommendation, we set ${\lambda }_3,and{\lambda }_4=0$, causing the CNNMF framework to boil down as in Equation (7), then eliminate “time”, “weather”, “season”, “tags”, and “geographical distance” information, respectively. The results are given in

Table 3. The performance of eliminating different types of information (results indicated as (mean ± standard deviation)).

Performance	Text (txt)	Distance (dis)	Season (s)	Weather (w)	Time (t)	CNNMF
MAP@1	0.456 ± 0.043	0.632 ± 0.051	0.397 ± 0.045	0.446 ± 0.082	0.492 ± 0.072	0.653 ± 0.012
MAP@5	0.320 ± 0.054	0.364 ± 0.066	0.281 ± 0.062	0.313 ± 0.082	0.322 ± 0.085	0.404 ± 0.013
MAP@10	0.215 ± 0.044	0.242 ± 0.072	0.191 ± 0.071	0.213 ± 0.063	0.219 ± 0.077	0.271 ± 0.022
MAP@20	0.136 ± 0.031	0.152 ± 0.043	0.122 ± 0.082	0.135 ± 0.065	0.139 ± 0.046	0.171 ± 0.011

, which can find the following tendencies:

• Diverse types of information enhance recommendation performance to diverse degrees. According to influence degree, the information can be ranked as follows: season information > weather information > text information > time information > geographical distance information. The performance of eliminating “season” information is the lowest, which means that “season” information is the most important information to recommend travel location. The performance of eliminating “geographical distance” information is the highest, which means that “geographical distance” information is the most unimportant information, as most travel locations are not far from each other.
• The MAP of the proposed method is significantly better than those of the five other variants, which demonstrated that the proposed method integrates contextual, textual, and geographical information together and can thus provide improved recommendations.

5.5. The Performance Comparison of Recommendation Methods

To investigate the capability of the proposed method to recommend travel locations, we compared it with the following representative methods.

• Dynamic topic model and matrix factorization (DTMMF): DTMMF integrates topic model with matrix factorization to recommend travel locations. DTM is used to obtain implicit information, while explicit information is obtained from past check-ins and visual contents (i.e., age and gender) to construct user and travel location profiles [9].
• Neural network-based Collaborative Filtering (NCF): NCF combines matrix factorization with multi-layer perceptron to capture nonlinear user–travel location interactions [41]. Visual content is not considered.
• Visual-enhanced probabilistic matrix factorization model (VPMF): VPMF uses visual features to learn user preferences by leveraging the past check-ins of users. Then, it integrates user preferences with travel location constraints for trip planning [42].
• Visual Bayesian personalized ranking (VBPR): VBPR extracts the visual features from photos using a pre-trained method without any context information [5]. The extracted visual feature is used to predict the scores of people’s opinions.
• Visual Content Enhanced POI recommendation (VPOI): VPOI uses joint learning of photo classification, matrix decomposition, and visual feature extraction tasks [29], to recommend travel locations to the user. The difference with the proposed method is that VPOI uses photos for joint learning of the latent factor vector representations.

For fairness, all representative methods include the same total number of dimensions. The results are given in

Table 4. The performance comparison of recommendation methods (results indicated as (mean ± standard deviation)) in terms of MAP@n.

Performance	(a)	(b)	(c)	(d)	(e)	(f)	Improv.
	DTMMF	NCF	VPMF	VBPR	VPOI	CNNMF	f vs. best
MAP@1	0.475 ± 0.061	0.492 ± 0.071	0.512 ± 0.061	0.584 ± 0.029	0.623 ± 0.097	0.662 ± 0.018	6.26%
MAP@5	0.358 ± 0.081	0.359 ± 0.039	0.351 ± 0.081	0.367 ± 0.074	0.391 ± 0.075	0.415 ± 0.012	6.19%
MAP@10	0.198 ± 0.072	0.200 ± 0.073	0.201 ± 0.072	0.203 ± 0.077	0.231 ± 0.070	0.271 ± 0.022	17.32%
MAP@20	0.115 ± 0.025	0.118 ± 0.085	0.120 ± 0.025	0.130 ± 0.098	0.158 ± 0.041	0.171 ± 0.013	8.23%

, and the following observations can be found:

• The proposed method beats other methods, i.e., DTMMF, NCF, VPMF, VBPR and VPOI, respectively, on average 35.21%, 32.65%, 31.22%, 22.87%, 9.5%.
• VPMF works better than DTMMF, which might be because VPMF extracts visual features directly from the whole photo, while DTMMF extracts only some attributes (i.e., age and gender) based on face recognition.
• VPOI works better than VBPR, which might be because VPOI models photos for both users and travel locations while VBPR only models photos for travel locations.
• The proposed method significantly outperforms VPOI. That is because of the incorporating of contextual (i.e., time, weather, and season), textual (i.e., tags), and geographical (i.e., distance) information, while VPOI only uses photos for joint learning of the latent factor vector representations.

We compare our framework with the same above-mentioned representative methods for addressing the travel location cold start problem. We randomly select 5% of the travel locations’ photos from the training set and remove their check-ins. Moreover, we remove the photo albums from the remaining 20% and use them as the testing set. All photo albums are associated with check-ins in our Flickr dataset. These travel locations (5%) will still have photos without any check-ins, which can help mitigate the travel location cold start problem. The results are given in

Table 5. The performance with 5% cold start travel locations in terms of MAP@n. (The numbers inside parentheses indicate the performance reductions compared to the performance without location cold start, as shown in Table 4).

Performance	(a)	(b)	(c)	(d)	(e)	(f)	Improv.
	DTMMF	NCF	VPMF	VBPR	VPOI	CNNMF	f vs. best
MAP@1	0.421 (11.37%)	0.441 (11.56%)	0.454 (11.33%)	0.532 (8.90%)	0.585 (6.10%)	0.623 (5.89%)	6.50%
MAP@5	0.315 (12.01%)	0.318 (11.42%)	0.320 (8.83%)	0.331 (9.81%)	0.362 (7.42%)	0.395 (4.82%)	9.12%
MAP@10	0.169 (14.65%)	0.173 (13.5%)	0.175 (12.94%)	0.182 (10.34%)	0.214 (7.36%)	0.255 (5.90%)	19.16%
MAP@20	0.101 (12.17%)	0.106 (10.17%)	0.105 (12.50%)	0.116 (10.77%)	0.145 (8.23%)	0.162 (5.26%)	11.73%

, and the following observations can be found:

• In general, the performance of all methods drops when we present the travel location cold start problem. For example, the performance of DTMMF decreases up to 14.65% in terms of MAP@10.
• The proposed method beats other methods, i.e., DTMMF, NCF, VPMF, VBPR and VPOI, respectively, on average 40.17%, 41.43, 40.17%, 29.06%, 11.63%, for cold start travel locations.
• The performance reduction of VBPR is much smaller than that of DTMMF, as VBPR learns an additional layer to exploit the visual dimensions, which can help to alleviate the travel location cold start problem, while DTMMF uses visual contents only to extract attributes (i.e., age and gender) based on face recognition.
• The proposed method of CNNMF significantly outperforms VPOI, while both methods use visual contents. The differences between the CNNMF and VPOI include: CNNMF directly obtains latent factor from its photos as descriptions of travel locations; while VPOI uses photos to help learn the latent factor vector representation.

6. Conclusions and Future Work

In this study, we propose a CNNMF that integrates CNN and WMF to obtain the latent factor representations for new travel locations. We use similarity weight between users (and travel locations) to exploit auxiliary attributes, which are integrated into the WMF process to recommend travel locations. If a travel location does not have past check-ins, the proposed method uses CNN to estimate its latent factor representation from its photos. Experimental results demonstrate that CNNMF significantly outperforms existing methods. Future research can extend in the following directions: (i) extract more information from photos (e.g., social correlations), which can help to mitigate the user cold start problem; (ii) incorporate other competitive recommendation methods.