Multidisciplinary Optimization and Analysis of Stratospheric Airships Powered by Solar Arrays
Abstract
:1. Introduction
2. Theory
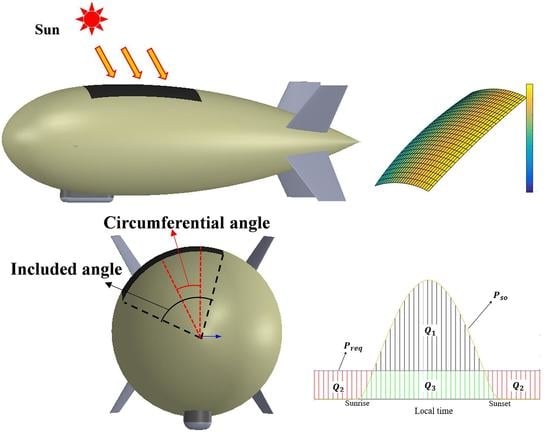
2.1. Airship Geometry Model
2.2. Output Power Model of Solar Array
2.2.1. Solar Radiation Flux Model
2.2.2. Position of the Sun
2.2.3. Output Power Model of Solar Array
2.3. Energy Balance Model
2.4. Buoyancy Balance Model
3. Optimization Method
3.1. Optimization Methodology
3.2. Variables and Constants
3.3. Objective Function and Constraints
4. Results and Discussions
4.1. Optimization on the Baseline Model
4.2. Effects of Latitudes
4.3. Effects of Heading Angles
4.4. Effects of Average Resisting Wind Speeds
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Airship length | |
| Airship diameter | |
| Volume of airship | |
| Surface of the airship | |
| Fineness ratio of airship | |
| Solar radiation flux | |
| Atmospheric transmittance | |
| Flight altitude | |
| Sun elevation angle | |
| Declination angle of the sun | |
| Latitude of flight | |
| Hour angle of the sun | |
| Solar radiation flux of the exoatmosphere | |
| Position vector of the sun | |
| Sun azimuth angle | |
| Day angle of the sun | |
| Hour angle of the sun | |
| Local mean solar time | |
| Local longitude | |
| Reference longitude for the local time zone | |
| Time difference between actual solar time and mean solar time | |
| Circumferential radius of the element | |
| Normal vector of the element surface | |
| Total included angle of the solar array | |
| Heading angle of the airship | |
| Pitch angle of the airship | |
| Roll angle of the airship | |
| Power received by element | |
| Total area of solar arrays | |
| Central angle of the solar array | |
| Included angle of the solar array | |
| Power required for an airship | |
| Power consumed by the propulsion subsystem | |
| Drag coefficient of the airship | |
| Available surplus energy for storage in lithium battery when | |
| Energy consumption which needs to be supplied by the lithium battery | |
| Energy generated by solar arrays which is used for running the airship | |
| Buoyancy of the airship | |
| Total mass of the airship | |
| Total mass of the structural subsystem | |
| Total mass of the energy subsystem | |
| Mass of the propulsion subsystem | |
| Mass of the payload | |
| Mass of the other components | |
| Mass of the airship envelope | |
| Mass of the fin | |
| Mass of the gas in the airship | |
| Sum of mass of the solar array | |
| Mass of the solar array | |
| Mass of the lithium battery | |
| Power density of the propulsion subsystem |
References
- Tang, J.; Xie, W.; Wang, X.; Chen, C. Simulation and Analysis of Fluid–Solid–Thermal Unidirectional Coupling of Near-Space Airship. Aerospace 2022, 9, 439. [Google Scholar] [CrossRef]
- Liu, S.; Sang, Y. Underactuated Stratospheric Airship Trajectory Control Using an Adaptive Integral Backstepping Approach. J. Aircr. 2018, 55, 2357–2371. [Google Scholar] [CrossRef]
- Alam, M.I.; Pant, R.S. Estimation of Volumetric Drag Coefficient of Two-Dimensional Body of Revolution. J. Aircr. 2019, 56, 2080–2082. [Google Scholar] [CrossRef]
- Tang, J.; Wang, X.; Duan, D.; Xie, W. Optimisation and analysis of efficiency for contra-rotating propellers for high-altitude airships. Aeronaut. J. 2019, 123, 706–726. [Google Scholar] [CrossRef]
- Yoder, C.D.; Agrawal, S.; Motes, A.G.; Mazzoleni, A.P. Aerodynamic Tethered Sails for Scientific Balloon Trajectory Control: Small-Scale Experimental Demonstration. J. Aircr. 2021, 58, 1. [Google Scholar] [CrossRef]
- Robyr, J.-L.; Bourquin, V.; Goetschi, D.; Schroeter, N.; Baltensperger, R. Modeling the Vertical Motion of a Zero Pressure Gas Balloon. J. Aircr. 2020, 57, 991–994. [Google Scholar] [CrossRef]
- Colozza, A. PV/regenerative fuel cell high altitude airship feasibility study. In Proceedings of the 2nd AIAA “Unmanned Unlimited” Conference and Workshop & Exhibit, AIAA 2003-6663, San Diego, CA, USA, 15–18 September 2003. [Google Scholar] [CrossRef]
- Hoshino, T.; Okaya, S.; Fujiwara, T.; Miwa, S.; Nomura, Y.; Naito, H.; Eguchi, K. Design and analysis of solar power system for SPF airship operations. In Proceedings of the 13th AIAA Lighter-Than Air Technology Conference, Norfolk, VA, USA, 28 June–1 July 1999. [Google Scholar] [CrossRef]
- Wang, H.; Song, B.; Zuo, L. Effect of High-Altitude Airship’s Attitude on Performance of its Energy System. J. Aircr. 2007, 44, 2077–2080. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Lv, M.; Tan, D.; Zhu, W.; Sun, K. Simplified Analytical Model for Investigating the Output Power of Solar Array on Stratospheric Airship. Int. J. Aeronaut. Space Sci. 2016, 17, 432–441. [Google Scholar] [CrossRef]
- Du, H.; Zhu, W.; Wu, Y.; Zhang, L.; Li, J.; Lv, M. Effect of angular losses on the output performance of solar array on long-endurance stratospheric airship. Energy Convers. Manag. 2017, 147, 135–144. [Google Scholar] [CrossRef]
- Zhu, W.; Li, J.; Xu, Y. Optimum attitude planning of near-space solar powered airship. Aerosp. Sci. Technol. 2019, 84, 291–305. [Google Scholar] [CrossRef]
- Alam, M.I.; Pant, R.S. A multi-node model for transient heat transfer analysis of stratospheric airships. Adv. Space Res. 2017, 59, 3023–3035. [Google Scholar] [CrossRef]
- Alam, M.I.; Pant, R.S. Multidisciplinary approach for solar area optimization of high altitude airships. Energy Convers. Manag. 2018, 164, 301–310. [Google Scholar] [CrossRef]
- Garg, A.; Burnwal, S.; Pallapothu, A.; Alawa, R.; Ghosh, A. Solar Panel Area Estimation and Optimization for Geostationary Stratospheric Airships. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011. [Google Scholar] [CrossRef]
- Li, J.; Lv, M.; Sun, K. Optimum area of solar array for stratospheric solar-powered airship. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 231, 2654–2665. [Google Scholar] [CrossRef]
- Liang, H.; Zhu, M.; Guo, X.; Zheng, Z. Conceptual Design Optimization of High Altitude Airship in Concurrent Subspace Optimization. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition; AIAA 2012-1180, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, Y.; Li, J.; Du, H.; Zhang, L. Research on optimal solar array layout for near-space airship with thermal effect. Sol. Energy 2018, 170, 1–13. [Google Scholar] [CrossRef]
- Wang, Q.-B.; Chen, J.-A.; Fu, G.-Y.; Duan, D.-P. An approach for shape optimization of stratosphere airships based on multidisciplinary design optimization. J. Zhejiang Univ. A 2009, 10, 1609–1616. [Google Scholar] [CrossRef]
- Trancossi, M.; Dumas, A.; Madonia, M. Energy and Mission Optimization of an Airship by Constructal Design for Efficiency Method. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013. [Google Scholar] [CrossRef]
- Shan, C.; Lv, M.; Sun, K.; Gao, J. Analysis of energy system configuration and energy balance for stratospheric airship based on position energy storage strategy. Aerosp. Sci. Technol. 2020, 101, 105844. [Google Scholar] [CrossRef]
- Ceruti, A.; Gambacorta, D.; Marzocca, P. Unconventional hybrid airships design optimization accounting for added masses. Aerosp. Sci. Technol. 2018, 72, 164–173. [Google Scholar] [CrossRef]
- Meng, J.; Li, M.; Ma, N.; Liu, L. Multidisciplinary design optimization of a lift-type hybrid airship. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 72–83. [Google Scholar] [CrossRef]
- Zhang, L.; Lv, M.; Zhu, W.; Du, H.; Meng, J.; Li, J. Mission-based multidisciplinary optimization of solar-powered hybrid airship. Energy Convers. Manag. 2019, 185, 44–54. [Google Scholar] [CrossRef]
- Tang, J.; Duan, D.; Xie, W. Shape Exploration and Multidisciplinary Optimization Method of Semirigid Nearing Space Airships. J. Aircr. 2021, 59, 946–963. [Google Scholar] [CrossRef]
- Zhang, L.; Lv, M.; Meng, J.; Du, H. Conceptual design and analysis of hybrid airships with renewable energy. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 2144–2159. [Google Scholar] [CrossRef]
- Zhang, L.; Lv, M.; Meng, J.; Du, H. Optimization of solar-powered hybrid airship conceptual design. Aerosp. Sci. Technol. 2017, 65, 54–61. [Google Scholar] [CrossRef]
- Lv, M.; Li, J.; Du, H.; Zhu, W.; Meng, J. Solar array layout optimization for stratospheric airships using numerical method. Energy Convers. Manag. 2017, 135, 160–169. [Google Scholar] [CrossRef]
- Lv, M.; Li, J.; Zhu, W.; Du, H.; Meng, J.; Sun, K. A theoretical study of rotatable renewable energy system for stratospheric airship. Energy Convers. Manag. 2017, 140, 51–61. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, W.; Du, H.; Lv, M. Multidisciplinary design of high altitude airship based on solar energy optimization. Aerosp. Sci. Technol. 2021, 110, 106440. [Google Scholar] [CrossRef]
- Pant, R. A Methodology for Determination of Baseline Specifications of a Non-Rigid Airship. In Proceedings of the AIAA’s 3rd Annual Aviation Technology, Integration, and Operations Conference (ATIO), AIAA 2003-6830, Denver, CO, USA, 17–19 November 2003. [Google Scholar] [CrossRef]
- Yang, X.; Liu, D. Renewable power system simulation and endurance analysis for stratospheric airships. Renew. Energy 2017, 113, 1070–1076. [Google Scholar] [CrossRef]
- Farley, R. Balloon Ascent: 3-D Simulation Tool for the Ascent and Float of High-Altitude Balloons. In Proceedings of the AIAA’s 5th Aviation, Technology, Integration, and Operations Conference (ATIO), AIAA 2005-7412, Arlington, VA, USA, 26–28 September 2005. [Google Scholar] [CrossRef]
- Kalogirou, S. Solar Energy Engineering—Processes and Systems, 1st ed.; Elsevier: London, UK, 2009. [Google Scholar]
- Palumbo, R.; Russo, M.; Filippone, E.; Corraro, F. ACHAB: Analysis Code for High-Altitude Balloons. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, AIAA 2007-6642, Hilton Head, SC, USA, 20–23 August 2007. [Google Scholar] [CrossRef]
- Gui, W.; Li, T.; Lu, Y. Improvement of solar position formula and its application. Water Resour. Power 2011, 29, 213–216. [Google Scholar]
- Hoerner, S. Fluid-Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance; Fluid Dynamics: Midland Park, NJ, USA, 1965; Available online: https://n2t.net/ark:/13960/t57f0bk2j (accessed on 1 January 2022).
- Cheeseman, I. Airship Technology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Yang, B. Formulization of standard atmospheric parameters. J. Astronaut. 1983, 1, 83–86. [Google Scholar]
- Colozza, A.; Dolce, J. Initial Feasibility Assessment of a High Altitude Long Endurance Airship, NASA/CR. 2003. Available online: https://ntrs.nasa.gov/citations/20040021326 (accessed on 11 December 2022).
- Zhang, W.-W.; Qi, H.; Yu, Z.-Q.; He, M.-J.; Ren, Y.-T.; Li, Y. Optimization configuration of selective solar absorber using multi-island genetic algorithm. Sol. Energy 2021, 224, 947–955. [Google Scholar] [CrossRef]
- Schittkowski, K. NLPQL: A fortran subroutine solving constrained nonlinear programming problems. Ann. Oper. Res. 1986, 5, 485–500. [Google Scholar] [CrossRef]






















| Full Name of Parameters | Parameter | Lower Bound | Upper Bound |
|---|---|---|---|
| Semimajor axis of the front part of airship (m) | 50 | 150 | |
| Semimajor axis of the rear part of airship (m) | 50 | 150 | |
| Fineness ratio of airship | 3 | 5 | |
| Horizontal distance from the airship nose to the front of solar arrays (m) | 20 | 100 | |
| Horizontal distance from the airship nose to the rear of solar arrays (m) | 50.0 | 200.0 | |
| Included angle of solar arrays () | 60 | 180 | |
| Central angle of solar arrays () | −30.0 | 90 |
| Full Name of Parameters | Parameter | Value |
|---|---|---|
| Transformation efficiency of the solar cell (%) | 18 | |
| Efficiency of propulsion subsystem (%) | 55 | |
| Charge efficiency of lithium battery (%) | 95 | |
| Discharge efficiency of lithium battery (%) | 98 | |
| Areal density of solar arrays (kg/m2) | 0.65 | |
| Areal density of envelope (kg/m2) | 0.125 | |
| Areal density of fin (kg/m2) | 0.06 | |
| Energy density of battery (Wh/kg) | 200 | |
| Power density of propulsion subsystem (W/kg) | 222 | |
| Power consumed by control system (W) | 1000 | |
| Power consumed by payload (W) | 5000 | |
| Mass of payload (kg) | 500 | |
| Average flight speed of airship (m/s) | 25 | |
| Maximum flight speed of airship (m/s) | 30 |
| Parameter | Arbitrary Baseline | Optimized | Relative Difference (%) |
|---|---|---|---|
| Volume of airship (m3) | 405,690 | 325,257 | −19.83 |
| Length of airship (m) | 247 | 243.3 | −1.5 |
| Fineness ratio | 4.40 | 4.80 | 9.19 |
| Mass of solar array (kg) | 2669.4 | 1507.9 | −43.51 |
| Mass of storage (kg) | 14,222 | 11,389 | −19.91 |
| Total mass of energy system (kg) | 16,891 | 12,897 | −23.65 |
| Total mass of airship (kg) | 35,708 | 28,629 | −19.82 |
| Requested averaged power (kW) | 198 | 171 | −13.63 |
| Area of solar array (m3) | 4106.8 | 2319.7 | −43.51 |
| Central angle of solar array () | 0.0 | 295.7 | - |
| Included angle of solar array () | 87.75 | 50.06 | - |
| Start of solar array (m) | 70 | 55.08 | - |
| Horizontal projection length of solar array (m) | 100 | 108.46 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Xie, W.; Zhou, P.; Yang, H.; Zhang, T.; Wang, Q. Multidisciplinary Optimization and Analysis of Stratospheric Airships Powered by Solar Arrays. Aerospace 2023, 10, 43. https://doi.org/10.3390/aerospace10010043
Tang J, Xie W, Zhou P, Yang H, Zhang T, Wang Q. Multidisciplinary Optimization and Analysis of Stratospheric Airships Powered by Solar Arrays. Aerospace. 2023; 10(1):43. https://doi.org/10.3390/aerospace10010043
Chicago/Turabian StyleTang, Jiwei, Weicheng Xie, Pingfang Zhou, Hui Yang, Tongxin Zhang, and Quanbao Wang. 2023. "Multidisciplinary Optimization and Analysis of Stratospheric Airships Powered by Solar Arrays" Aerospace 10, no. 1: 43. https://doi.org/10.3390/aerospace10010043
APA StyleTang, J., Xie, W., Zhou, P., Yang, H., Zhang, T., & Wang, Q. (2023). Multidisciplinary Optimization and Analysis of Stratospheric Airships Powered by Solar Arrays. Aerospace, 10(1), 43. https://doi.org/10.3390/aerospace10010043