Supersonic Flow Control Using Combined Energy Deposition ^†

Abstract

Drag force control via energy deposition in an oncoming flow is a wide area of interest in aerospace sciences. Recently, investigations on the effect of combining energy sources have been conducted. The possibility of coupling microwave (MW) discharges or MW and laser energy deposition is discussed. In the present work, the flow details accompanying the interaction of a combined energy release and an aerodynamic body in a supersonic flow are considered numerically on the base of the Euler equations. Comparison with non-combined energy deposition is analyzed. The effect of introducing the internal part to the energy release on the drag force reduction is examined. The flows for blunt cylinder, hemisphere-cylinder and pointed body are considered for a wide class of the combined energy source characteristics. Freestream Mach number is varied from 1.89 to 3.45. Complicated unsteady vortex structures caused by the Richtmyer–Meshkov instabilities are shown to be the reason for the reduction in drag. The unsteady double vortex mechanism of the frontal drag force reduction and mechanism of the constantly acting vortices at the steady flow are described. Suppression of shear layer instability and large scaled flow pulsations as the result of the combined energy release effect is established. Complex conservative difference schemes are used in the simulations.

1. Introduction

The problem of unsteady interaction of a space distributed energy source dislocated in an oncoming supersonic flow with a shock layer was initiated in [1] on the example of the flow past a sphere. Energy source was shown to produce a significant effect causing total flow reconstruction. This phenomenon has been considered for the purpose of flow control via changing characteristics of an aerodynamic body (see survey in [2]). In [3], the effect of a heated rarefied channel on a supersonic flow past a blunt cylinder is examined. On the base of this model the microwave (MW) plasmoid was shown to be effective for drag force reduction [4]. It is obtained that the vortex flow generated at the first stage of the interaction causes decreasing in the frontal drag force. The vorticity production was shown to be connected with the Richtmyer–Meshkov instability which is the result of the bow shock wave accelerating effect on the boundaries of the heated area [5]. In [6,7,8,9], the research of the flow details during homogeneous MW filament/shock layer interaction is presented for a wide class of oncoming parameters. In [10], the effect of a longitudinal gas area characterized by the high temperature profile is modeled for the evaluation of the laser discharge influence on the flow past a blunt cylinder at M = 3. Combining energy sources is a new direction in the area of the energy influenced flow control technologies. The effect of combining energy sources was pointed out experimentally for the coupled MW–laser energy supply in [11]. Numerical model of a combined energy deposition was suggested and examined in [12,13]. Also, this model can be used for essentially inhomogeneous heat areas produced by non-combined energy sources [14].

In the present paper, the interaction of a combined energy release with a supersonic flow past blunt bodies (cylinder and hemisphere-cylinder) and a pointed body is considered numerically using the Euler equations. Energy release is supposed to have a shape of heated rarefied channel/channels. Flow analysis for a wide class of the parameters of the energy source is conducted. The double vortex mechanism of the frontal drag force reduction is examined for unsteady flow past the blunt bodies. Suppression of the shear layer instability and large scale flow pulsations is researched for the constantly acting energy sources. The mechanism of the frontal drag force reduction connected with the constantly acting vortices is examined for the steady flow past the pointed body. Quantitative results on drag reduction for the considered simplest shapes of aerodynamic bodies are presented.

2. Methodology

The modeling of the interaction of a combined energy source with a supersonic shock layer is based on the Euler equations for a perfect gas for planar and cylinder flow symmetry:

$$\frac{\partial U{r}^{\omega }}{\partial t}+\frac{\partial F{r}^{\omega }}{\partial x}+\frac{\partial G{r}^{\omega }}{\partial r}=H$$

(1)

$$U=\left(\begin{array}{c}\rho \\ \rho u\\ \rho v\\ E_S\end{array}\right),F=\left(\begin{array}{c}\rho u\\ p+\rho u^2\\ \rho uv\\ u(E_S+p)\end{array}\right),G=\left(\begin{array}{c}\rho v\\ \rho uv\\ p+\rho v^2\\ v(E_S+p)\end{array}\right),H=\left(\begin{array}{c}0\\ 0\\ \omega p\\ 0\end{array}\right)$$

(2)

here ω = 0/1 for plane/cylindrical flow, ρ, p—density and pressure of the gas, u and v are x- and r-components of the gas velocity, E_S = ρ(ε + 0.5(u² + v²)), ε = p/(γ(ρ − 1)), γ = 1.4. A flow reconstruction past bodies of different shapes with the axis parallel to the oncoming flow is examined; the calculation area is bounded by the axis of symmetry (Figure 1). Mach number of the oncoming flow was varied from 1.89 to 3.45. The non-dimensional undisturbed flow parameters corresponding to the normal conditions are ρ_∞ = 1, p_∞ = 0.2, u_∞ = 1, v_∞ = 0. Normalizing parameters for pressure, density and length are p_n = 5 × 1.01325 × 10⁵ Pa, ρ_n = 1.29 kg m⁻³, l_n = 10⁻¹ m, which give for time and velocity: t_n = 159.57 µs and u_n = 626.7 m s⁻¹.

Figure 1. Schematic of the flow and accepted notations.

Figure 1. Schematic of the flow and accepted notations.

Initial condition is the converged steady flow past the body. At the inflow boundary the freestream parameters are specified and the slip boundary conditions are utilized on the body’s boundaries and on the axis of symmetry. No-reflection boundary conditions in the directions normal to the boundaries are used on the exit boundaries.

Energy deposition is modeled via the creation of heated rarefied layer/layers (“filament” or “combined filament”). The non-combined filament of the diameter d is modeled via the inflow boundary condition (x = 0) as a channel of low density ρ_i where ρ_i = α_ρρ_∞ for 0 ≤ r ≤ 0.5d (subscript “∞” refers to the freestream parameters). The static pressure and velocity of the channel are equal to those of the undisturbed flow. In the model of the combined energy deposition another heat layer of the diameter d₁ is formed inside the primary layer characterized by the parameter of the gas rarefaction α_ρ1. Thus ρ_i = α_ρρ_∞ for 0.5d₁ ≤ r ≤ 0.5d and ρ_i = α_ρρ_∞ for 0 ≤ r ≤ 0.5d₁ (Figure 1). The energy source is supposed to arise instantly in the steady flow in front of the bow shock wave at the time moment t_i. At this moment the differences between the theoretical and computational parameters at the stagnation point are about 1%–2%.

The simulations are based on the complex conservative difference schemes. The schemes are explicit and use the Lax’s scheme stencil. To obtain the second approximation order in space and in time the enlarged complex of the conservative variables including the additional conservative variables for the space derivatives is applied. Details of the scheme construction for a cylinder flow are presented in [15]. The special modifications of the schemes provide for the inclusion of the body’s boundaries into the calculation area without breaking the conservation laws (see [16]). In the calculations below, the schemes are used without the introduction of any additional monotony providing operators. The staggered Cartesian difference grids with equal space steps, h_x = h_r, and the distance between the nodes equal to 2h_x, 2h_r are used (Table 1). To determine the time step the CFL condition of stability is used with the coefficient varying within 0.5–0.9. In Section 3.1, Section 3.2 and Section 3.3 the fine grid is used, in Section 3.4 we use the coarse grid. The results of test calculations upon comparison of a number of theoretical/experimental values with the computational ones for the considered flows are presented in [7]. The difference between the computed parameters and theoretical/experimental ones varies from 1.2% to 2.7%. The examples of the computational convergence with decreasing space steps and the grid independence study are presented in [15,16] and discussed in Section 3.5.

Table 1. Using difference grids.

Characteristics	Coarse Grid	Fine Grid
hx, hr	0.0008	0.0005
Number of nodes per D	125	400

Table 1. Using difference grids.

Characteristics	Coarse Grid	Fine Grid
hx, hr	0.0008	0.0005
Number of nodes per D	125	400

3. Results and Discussion

3.1. Interaction of the Bounded Combined Filament with the Supersonic Blunt Cylinder

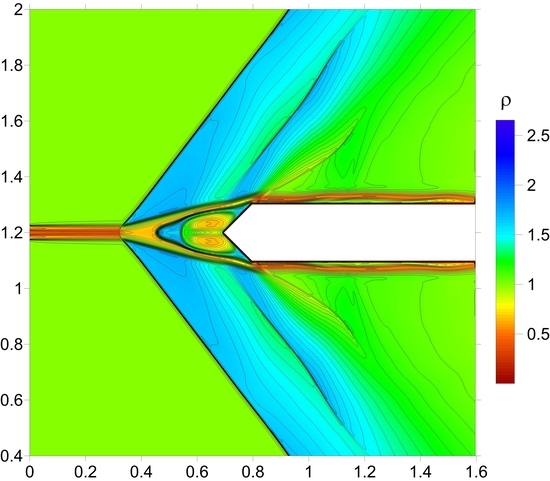
Consider the interaction of the bounded combined filament with the supersonic cylinder shock layer in the case of α_ρ1 < α_ρ. This means that the temperature of the gas in the internal part of the filament is greater than in the external one. The dynamics of density are presented in Figure 2a,b (Δl = 4D, dimensionless time moments are indicated), and below in Section 3.1 and Section 3.2 t_i = 13.01. Two density stratified vortices caused by the Richtmyer–Meshkov instabilities are seen to be formed in front of the body. The density stratified structure of these vortices is caused by the rolling contact discontinuities (boundaries of the energy source) under the accelerating effect of the bow shock wave [5]. Gas inside these vortices is rotating clockwise. The corresponding pressure fields demonstrate the presence of two points of local minima (at the centers of these vortexes) and the complicated lambda-waves configuration which arises above the vortices. Also, the piece-wise linear fracture of the bow shock wave front is forming (Figure 2c,d).

The dynamics of the density field in the case of α_ρ1 > α_ρ when the temperature of the gas in the internal part of the filament is smaller than in the external one is presented in Figure 3a,b. Two vortices accompanying the Richtmyer–Meshkov instabilities are seen. The upper vortex is rotating clockwise; the lower vortex is rotating counterclockwise. The according pressure fields are presented in Figure 3c,d. The vortex structure causes the reduction of the frontal drag force, too, but to a lesser degree than in the previous case.

Figure 4 demonstrates the face drag force dynamics for different α_ρ1. Here, the drag force is normalized by its value in the absence of energy deposition F₀. It is seen that, the higher density in the internal filament, the smaller the drop in the drag force that is obtained. For α_ρ1 < α_ρ the second vortex from the internal part enhances the effect from the first one and as a result the drag force drop is also increased.

Figure 2. Generation of two vortices rotating clockwise as the result of the Richtmyer–Meshkov instabilities, d/D = 0.25, d₁/D = 0.075, α_ρ = 0.5, α_ρ1 = 0.35: (a,b) Density fields; (c,d) Pressure fields.

Figure 2. Generation of two vortices rotating clockwise as the result of the Richtmyer–Meshkov instabilities, d/D = 0.25, d₁/D = 0.075, α_ρ = 0.5, α_ρ1 = 0.35: (a,b) Density fields; (c,d) Pressure fields.

Figure 3. Generation of two vortices rotating in opposite directions as the result of the Richtmyer–Meshkov instabilities, d/D = 0.25, d₁/D = 0.075, α_ρ = 0.5, α_ρ1 = 0.75: (a,b) Density fields; (c,d) Pressure fields.

Figure 3. Generation of two vortices rotating in opposite directions as the result of the Richtmyer–Meshkov instabilities, d/D = 0.25, d₁/D = 0.075, α_ρ = 0.5, α_ρ1 = 0.75: (a,b) Density fields; (c,d) Pressure fields.

Figure 4. Dynamics of frontal drag force for non-combined and combined filaments for d/D = 0.25, Δl/D = 4, α_ρ = 0.5 and different values of α_ρ1 and d₁/D.

Figure 4. Dynamics of frontal drag force for non-combined and combined filaments for d/D = 0.25, Δl/D = 4, α_ρ = 0.5 and different values of α_ρ1 and d₁/D.

For α_ρ1 > α_ρ the second vortex weakens the first one and the opposite effect is seen in the drag force dynamics. Also, it shows that the results are weakly dependent on the value of d₁ (for two filaments with different d₁ the face drag force dynamics are quite similar—curves 2 and 3).

In Table 2 the drag force characteristics for the different parameters of the filaments are presented. For α_ρ = 0.5 and α_ρ1 = 0.35 the combining energy sources effect on drag force reduction of 18.8% (related to the non-combined filament) occurs.

Table 2. Blunt cylinder, M = 1.89.

Type of Filament	(F0 − Fmin)/F0 (%)
Non-combined, d/D = 0.25, αρ = 0.5	74.4
Combined, d/D = 0.25, d1/D = 0.125, αρ = 0.5, αρ1 = 0.35	88.4
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.5, αρ1 = 0.35	86.9
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.5, αρ1 = 0.65	63.6
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.5, αρ1 = 0.85	55.0

Table 2. Blunt cylinder, M = 1.89.

Type of Filament	(F0 − Fmin)/F0 (%)
Non-combined, d/D = 0.25, αρ = 0.5	74.4
Combined, d/D = 0.25, d1/D = 0.125, αρ = 0.5, αρ1 = 0.35	88.4
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.5, αρ1 = 0.35	86.9
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.5, αρ1 = 0.65	63.6
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.5, αρ1 = 0.85	55.0

3.2. Interaction of the Infinite Combined Filament with the Supersonic Blunt Cylinder

The effect of the infinite combined filament on the supersonic shock layer is examined. The interaction of the body’s face with the vortex structure is accompanied by the drag force reduction, the drop in the drag force being practically the same as in the case of the bounded energy release. The simulations show that the introduction of the internal part into the filament causes the qualitative reconstruction of the flow (Figure 5). For α_ρ1 < α_ρ introduction of the internal part stabilizes the flow suppressing the shear layer Kelvin–Helmholtz instability (or decreasing the scale of the vortices).

Figure 5a shows the line of vortices accompanying this instability in the case of non-combined (homogeneous) filament. In Figure 5b the suppression of this instability is seen for the external part of the combined filament, this instability being produced only by the internal part of the filament. For α_ρ1 > α_ρ the suppression does not take place; the lines of vortices are generating from the external part of the filament. Also, one can see two heated layers arising in front of the body (t = 15.2) the layer neighboring to the axis is colder than the surrounding one. So in this case forming the combined filament favors the transport of the heated gas to the body’s surface.

Figure 5. Density contours, M = 1.89, α_ρ = 0.5: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.4; (c) Combined filament, α_ρ1 = 0.75.

Figure 5. Density contours, M = 1.89, α_ρ = 0.5: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.4; (c) Combined filament, α_ρ1 = 0.75.

In addition, the most important effect of the combined energy release is the suppression of the large scaled pulsations which are inherent to the flows produced by the homogeneous (non-combined) energy sources. The pulsating flow mode is established for the considered flow parameters in [5,7]. Compare the frontal drag force dynamics in the case of the non-combined filament (Figure 6a) and produced by the same external filament with the introduced internal parts (Figure 6b,c). It can be pointed out that the combined energy deposition favors the suppression of the large scaled flow pulsations via predominance of the small scaled fluctuations. Also, it is seen that the mean values of the drag force in the statistically steady state are smaller for smaller α_ρ1.

Figure 6. Dynamics of dimensionless frontal drag force, M = 1.89, α_ρ = 0.5: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.4; (c) Combined filament, α_ρ1 = 0.75.

Figure 6. Dynamics of dimensionless frontal drag force, M = 1.89, α_ρ = 0.5: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.4; (c) Combined filament, α_ρ1 = 0.75.

These results are confirmed for the flow at M = 3. In Table 3 the characteristics of the front drag force are presented during the first pulsation. It is seen that even for the moderate values of the gas rarefaction in the combined energy source the effect is 19.0% (and can be increased via decreasing α_ρ and α_ρ1). It is also seen, that in the statistically steady state the small scaled fluctuations prevail over the large scaled pulsations and the averaged drag force values are smaller for smaller α_ρ1 (Figure 7, t_i = 6.01).

Table 3. Blunt cylinder, M = 3.

Type of Filament	(F0 − Fmin)/F0 (%)
Non-combined, d/D = 0.25, αρ = 0.65	74.2
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.65, αρ1 = 0.5	88.3

Table 3. Blunt cylinder, M = 3.

Type of Filament	(F0 − Fmin)/F0 (%)
Non-combined, d/D = 0.25, αρ = 0.65	74.2
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.65, αρ1 = 0.5	88.3

Figure 7. Dynamics of dimensionless frontal drag force, M = 3, α_ρ = 0.65: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.5.

Figure 7. Dynamics of dimensionless frontal drag force, M = 3, α_ρ = 0.65: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.5.

3.3. Interaction of the Combined Filament with the Supersonic Body “Hemisphere-Cylinder”

In this section the results of the interaction of different types of filaments with the supersonic body “hemisphere-cylinder” are presented (here t_i = 1.501). Superposition of two vortices’ effects on the half surface of the body (Figure 8). The effect from the energy deposition is weaker for this shape of body but introducing the internal part strengthens it by 51.7% (Figure 9a, see Table 4). For the infinite filaments, a similar effect is obtained at the steady state (Figure 9b).

Figure 8. Beginning of the interaction, M = 3.45, α_ρ = 0.5, α_ρ1 = 0.35, t = 1.74.

Figure 8. Beginning of the interaction, M = 3.45, α_ρ = 0.5, α_ρ1 = 0.35, t = 1.74.

Figure 9. Dynamics of dimensionless frontal drag force, M = 3.45, α_ρ = 0.5, α_ρ1 = 0.35: (a) Bounded filaments; (b) Infinite filaments.

Figure 9. Dynamics of dimensionless frontal drag force, M = 3.45, α_ρ = 0.5, α_ρ1 = 0.35: (a) Bounded filaments; (b) Infinite filaments.

Table 4. Hemisphere-cylinder, M = 3.45.

Type of Filament	(F0 − Fmin)/F0 (%)
Non-combined, d/D = 0.25, αρ = 0.5	23.6
Combined, d/D = 0.25, d1/D = 0.125, αρ = 0.5, αρ1 = 0.35	35.8

Table 4. Hemisphere-cylinder, M = 3.45.

Type of Filament	(F0 − Fmin)/F0 (%)
Non-combined, d/D = 0.25, αρ = 0.5	23.6
Combined, d/D = 0.25, d1/D = 0.125, αρ = 0.5, αρ1 = 0.35	35.8

3.4. Infinite Combined Filament/Supersonic Pointed Body Interaction

Consider the interaction of the infinite combined filament with the shock layer produced by the pointed body (with the half top angle equal to 45°) at M = 1.89 (t_i = 4.01). Here the flow is planar and the calculation area includes two symmetrical parts. It is seen that the symmetrical vortex structure causing by the Richtmyer–Meshkov instabilities is generated. While the vortex structure is moving to the body, the pressure on the face of the body falls, causing the drag force reduction.

Figure 10. Unsteady vortex structures in front of the body: density, α_ρ = 0.6: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.4; (c) Combined filament, α_ρ1 = 0.8.

Figure 10. Unsteady vortex structures in front of the body: density, α_ρ = 0.6: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.4; (c) Combined filament, α_ρ1 = 0.8.

Comparison of the unsteady vortex structures in front of the body for non-combined and combined filaments is presented in Figure 10. It is seen that for α_ρ1 > α_ρ the most complicated flow structure is obtained which is connected with the generation of the vortices rotating in opposite directions (Figure 10c). The corresponding steady flow modes are presented in Figure 11. One can conclude that these flow modes are quite different. The combined filament with α_ρ1 < α_ρ produces two constantly present vortices in front of the body (Figure 11b). The combined filament with α_ρ1 > α_ρ produces two weaker vortices and the streams of more cold gas in the areas neighboring to the axis of symmetry close to the pointed part of the body (Figure 11c).

Figure 11. Steady fields of density, α_ρ = 0.6: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.4; (c) Combined filament, α_ρ1 = 0.8.

Figure 11. Steady fields of density, α_ρ = 0.6: (a) Non-combined filament; (b) Combined filament, α_ρ1 = 0.4; (c) Combined filament, α_ρ1 = 0.8.

The dimensionless dynamics of the front drag force F are presented in Figure 12. It is seen that the combined filament with α_ρ1 < α_ρ causes much greater frontal drag force reduction than another ones. In Table 5 the face drag force values are presented during the first pulsation and for the steady flow mode (subscript “s”). It is seen that for α_ρ1 < α_ρ the effect of the combining energy sources achieves 60.8% (related to the non-combined one) for the first pulsation and 70.9% for the steady flow mode. The drag force reduction for α_ρ1 < α_ρ at the steady state is connected with two constantly effecting vortices in front of the body (Figure 11b). It should be mentioned that the coarse grid is used in this part and small flow details in Figure 12 are not resolved. However, in [15] it is shown that on a coarse grid the applied difference schemes give the steady values close to their mean values on a fine grid.

Figure 12. Dynamics of front drag force for different α_ρ1; α_ρ = 0.6.

Figure 12. Dynamics of front drag force for different α_ρ1; α_ρ = 0.6.

Table 5. Pointed body. M = 1.89.

Type of Filament	(F0 − Fmin)/F0 (%)	(F0 − Fs)/F0 (%)
Non-combined, d/D = 0.25, αρ = 0.6	38.3	28.5
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.6, αρ1 = 0.4	61.6	48.7
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.6, αρ1 = 0.8	34.8	25.2

Table 5. Pointed body. M = 1.89.

Type of Filament	(F0 − Fmin)/F0 (%)	(F0 − Fs)/F0 (%)
Non-combined, d/D = 0.25, αρ = 0.6	38.3	28.5
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.6, αρ1 = 0.4	61.6	48.7
Combined, d/D = 0.25, d1/D = 0.075, αρ = 0.6, αρ1 = 0.8	34.8	25.2

3.5. Examples of the Computational Convergence and Grid Independence

Consider the interaction of non-combined filament with supersonic shock layer over a blunt cylinder at M = 1.89. Figure 13 demonstrates the comparison of the results obtained with the use of three Cartesian difference grids with h_x = h_r (Table 6).

Table 6. Using difference grids.

Characteristics	Coarse Grid	Fine Grid I	Fine Grid II
hx, hr	0.001	0.0005	0.00012

Table 6. Using difference grids.

Characteristics	Coarse Grid	Fine Grid I	Fine Grid II
hx, hr	0.001	0.0005	0.00012

It is seen that at the stage of the drag force reduction caused by the primary vortex action in the calculations with the use of the coarse grid (Figure 13a) the main flow details are practically the same as in the case when the fine grid I is used (Figure 13b). In the drag force dynamics the small scale details are less visualized than on the fine grid I (Figure 13c). On the other hand, on the fine grid II the additional small scale details (secondary vortexes) are visualized and the base flow elements are retained (Figure 14a,b). It can be concluded that computational convergence with decreasing space steps takes place in the applied difference schemes. Also, the results show that the chosen grids are sufficiently sensitive and the results are grid-independent in the sense of retaining the base flow elements.

Figure 13. Density contours, t = 14.1: (a) Fine grid I; (b) Coarse grid (the body is moved on 0.05 to the right); (c) Front drag force dynamics: F₁—fine grid I, F₂—coarse grid; α_ρ = 0.5.

Figure 13. Density contours, t = 14.1: (a) Fine grid I; (b) Coarse grid (the body is moved on 0.05 to the right); (c) Front drag force dynamics: F₁—fine grid I, F₂—coarse grid; α_ρ = 0.5.

Figure 14. Density contours, α_ρ = 0.4: (a) Fine grid I; (b) Fine grid II.

Figure 14. Density contours, α_ρ = 0.4: (a) Fine grid I; (b) Fine grid II.

4. Conclusions

Drag force control via the effect of the combining of energy sources for a supersonic shock layer is proposed. The vortex mechanisms are indicated as executive factors for changing the body wave drag properties.

The intensification in the frontal drag force reduction up to 19% for a blunt cylinder and 52% for a hemisphere-cylinder is obtained via combining energy sources with α_ρ1 < α_ρ. This effect was shown to be connected with generation of two vortices rotating in one direction, the results being weakly dependent on the diameter of the internal filament. For α_ρ1 > α_ρ the generating vortices are rotating in opposite directions which decreases the drag force change. The suppression of the large scaled flow pulsations is shown, together with the additional suppression of the shear layer instability.

For the pointed body the structure of the unsteady and steady flow fields for different types of filaments is examined. The steady flow mode characterized by the constantly acting pair of vortices under the combined energy source effect is established. These vortices were shown to provide the considerable intensification (up to 71%) of the frontal drag force reduction.