Weather Impact on Airport Performance
Abstract
:1. Introduction
Structure of the Document
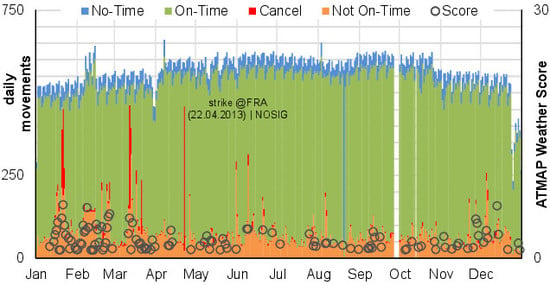
2. Data Set
2.1. Flight Plan
2.2. Weather Data
3. Performance Metric
3.1. ATMAP Algorithm
3.2. Airport Performance
3.2.1. Delay
3.2.2. Cancellations
4. Airport View
4.1. Correlation of Weather and Performance
4.2. Classification of Weather Effects
4.3. Days of Impact to Operational Performance
5. Network View
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ARR | Arrival |
| ATM | Air Traffic Management |
| ATFM | Air Traffic Flow Management |
| ATMAP | ATM Airport Performance |
| CB | Cumulonimbus Cloud |
| DEP | Departure |
| IATA | International Air Transport Association |
| ICAO | International Civil Aviation Organization |
| IFR | Instrument Flight Rules |
| METAR | Meteorological Aviation Routine Weather Report |
| PRU | Performance Review Unit |
| RVR | Runway Visual Range |
| SPECI | Special weather |
| TAF | Terminal Area/Aerodrome Forecast |
| TCU | Towering Cumulus |
| UTC | Coordinated Universal Time |
References
- EUROCONTROL. Performance Review Report—An Assessment of Air Traffic Management in Europe During the Calendar Year 2014, 2015, 2016; Technical Report; Performance Review Commission: Brussels, Belgium, 2017. [Google Scholar]
- Bronsvoort, J.; McDonald, G.; Porteous, R.; Gutt, E. Study of Aircraft Derived Temporal Prediction Accuracy using FANS. In Proceedings of the 13th Air Transport Research Society (ATRS) World Conference, Abu Dhabi, United Arab Emirates, 27–30 June 2009. [Google Scholar]
- Bongiorno, C.; Gurtner, G.; Lillo, F.; Mantegna, R.N.; Miccichè, S. Statistical characterization of deviations from planned flight trajectories in air traffic management. J. Air Trans. Manag. 2017, 58, 152–163. [Google Scholar] [CrossRef] [Green Version]
- Mueller, E.; Chatterji, G. Analysis of Aircraft Arrival and Departure Delay. In Proceedings of the AIAA ATIO Conference, Williamsburg, VA, USA, 6 November 2002. [Google Scholar]
- Tielrooij, M.; Borst, M.C.; van Paassen, M.; Mulder, M. Predicting Arrival Time Uncertainty from Actual Flight Information. In Proceedings of the 11th USA/Europe Air Traffic Management Research and Development Seminar (ATM 2015), Lisbon, Portugal, 23–26 June 2015. [Google Scholar]
- EUROCONTROL. CODA Digest All-Causes Delay and Cancellations to Air Transport in Europe—2016; Technical Report; Eurocontrol: Brussels, Belgium, 2016. [Google Scholar]
- Cook, A.; Tanner, G.; Enaud, P. Quantifying airline delay costs—The balance between strategic and tactical costs. In Proceedings of the 14th Air Transport Research Society (ATRS) World Conference, Porto, Portugal, 6–9 July 2010. [Google Scholar]
- Sohoni, M.G.; Erat, S. Can Time Buffers Lead to Delays? The Role of Operational Flexibility. SSRN 2015. [Google Scholar] [CrossRef] [Green Version]
- Rosenow, J.; Lindner, M.; Fricke, H. Impact of climate costs on airline network and trajectory optimization: A parametric study. CEAS Aeronaut. J. 2017, 8, 371–384. [Google Scholar] [CrossRef]
- Niklaß, M.; Lührs, B.; Grewe, V.; Dahlmann, K.; Luchkova, T.; Linke, F.; Gollnick, V. Potential to reduce the climate impact of aviation by climate restricted airspaces. Trans. Policy 2017. [Google Scholar] [CrossRef]
- Rosenow, J.; Fricke, H.; Luchkova, T.; Schultz, M. Minimizing contrail formation by rerouting around dynamic ice-supersaturated regions. Aeronaut. Aerosp. Open Access J. 2018, 2, 105–111. [Google Scholar] [CrossRef]
- Kaiser, M.; Rosenow, J.; Fricke, H.; Schultz, M. Tradeoff between optimum altitude and contrail layer to ensure maximum ecological en-route performance using the Enhanced Trajectory Prediction Model. In Proceedings of the 2nd International Conference on Application and Theory of Automation in Command and Control Systems (ATACCS 2012), London, UK, 28–30 May 2012. [Google Scholar]
- Oreschko, B.; Kunze, T.; Schultz, M.; Fricke, H.; Kumar, V.; Sherry, L. Turnaround prediction with stochastic process times and airport specific delay pattern. In Proceedings of the 5th International Conference on Research in Airport Transportation (ICRAT 2012), Berkeley, CA, USA, 22–25 May 2012. [Google Scholar]
- Gerdes, I.; Temme, A.; Schultz, M. Dynamic airspace sectorisation for flight-centric operations. Trans. Res. Part C Emerg. Technol. 2018, 95, 460–480. [Google Scholar] [CrossRef]
- Gerdes, I.; Temme, A.; Schultz, M. Dynamic airspace sectorization using controller task load. In Proceedings of the 6th SESAR Innovation Days (SID 2016), Delft, The Netherlands, 8–10 November 2016. [Google Scholar]
- Standfuß, T.; Gerdes, I.; Temme, A.; Schultz, M. Dynamic airspace optimisation. CEAS Aeronaut. J. 2018, 9, 517–531. [Google Scholar] [CrossRef]
- Schultz, M. Implementation and application of a stochastic aircraft boarding model. Trans. Res. Part C Emerg. Technol. 2018, 90, 334–349. [Google Scholar] [CrossRef]
- Schultz, M. Fast Aircraft Turnaround Enabled by Reliable Passenger Boarding. Aerospace 2018, 5, 8. [Google Scholar] [CrossRef]
- Grunewald, E.; Knabe, F.; Rudolph, F.; Schultz, M. Priority rules as a concept for the usage of scarce airport capacity. Trans. Res. Procedia 2018, 27, 1146–1153. [Google Scholar] [CrossRef]
- Schultz, M. Entwicklung eines Individuenbasierten Modells zur Abbildung des Bewegungsverhaltens von Passagieren im Flughafenterminal. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2010. [Google Scholar]
- Santos, B.F.; Wormer, M.M.E.C.; Achola, T.A.O.; Curran, R. Airline delay management problem with airport capacity constraints and priority decisions. J. Air Trans. Manag. 2017, 63, 34–44. [Google Scholar] [CrossRef]
- Carlier, S.; de Lépinay, I.; Hustache, J.; Jelinek, F. Environmental impact of air traffic flow management delays. In Proceedings of the 7th USA/Europe Air Traffic Management Research and Development Seminar (ATM 2007), Barcelona, Spain, 2–5 July 2007. [Google Scholar]
- Campanelli, B.; Fleurquin, P.; Arranz, A.; Etxebarria, I.; Ciruelos, C.; Eguíluz, V.M.; Ramasco, J.J. Comparing the modeling of delay propagation in the US and European air traffic networks. J. Air Trans. Manag. 2016, 56, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, N.; Netjasov, F.; Jovanović, R.; Starita, S.; Strauss, A. Air Traffic Flow Management slot allocation to minimize propagated delay and improve airport slot adherence. Trans. Res. Part A Policy Pract. 2017, 95, 183–197. [Google Scholar] [CrossRef]
- Cook, A.; Delgado, L.; Tanner, G.; Cristóbal, S. Measuring the cost of resilience. J. Air Trans. Manag. 2016, 56, 38–47. [Google Scholar] [CrossRef]
- Proag, S.L.; Proag, V. The Cost Benefit Analysis of Providing Resilience. Procedia Econ. Financ. 2014, 18, 361–368. [Google Scholar] [CrossRef]
- Cook, A.; Tanner, G.; Williams, V.; Meise, G. Dynamic cost indexing—Managing airline delay costs. J. Air Trans. Manag. 2009, 15, 26–35. [Google Scholar] [CrossRef]
- Islami, A.; Sun, M.; Chaimatanan, S.; Delahaye, D. Optimization of military missions impact on civilian 4D trajectories. In Proceedings of the ENRI International Workshop on ATM/CNS (EIWAC 2017), Tokyo, Japan, 6 November 2017. [Google Scholar]
- Luchkova, T.; Vujasinovic, R.; Lau, A.; Schultz, M. Analysis of Impacts an Eruption of Volcano Stromboli could have on European Air Traffic. In Proceedings of the 11th USA/Europe Air Traffic Management Research and Development Seminar (ATM 2015), Lisbon, Portugal, 23–26 June 2015. [Google Scholar]
- Kreuz, M.; Luchkova, T.; Schultz, M. Effect Of Restricted Airspace On The ATM System. In Proceedings of the World Conference on Transport Research (WCTR 2016), Shanghai, China, 26–31 May 2016. [Google Scholar]
- Rosenow, J.; Fricke, H.; Schultz, M. Air Traffic Simulation with 4D multi-criteria optimized trajectories. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 2589–2600. [Google Scholar]
- Kaltenhäuser, S.; Morlang, F.; Luchkova, T.; Hampe, J.; Sippel, M. Facilitating Sustainable Commercial Space Transportation Through an Efficient Integration into Air Traffic Management. New Space 2017, 5, 244–256. [Google Scholar] [CrossRef]
- Sunil, E.; Hoekstra, J.; Ellerbroek, J.; Bussink, F.; Nieuwenhuisen, D.; Vidosavljevic, A.; Kern, S. Metropolis: Relating Airspace Structure and Capacity for Extreme Traffic Densities. In Proceedings of the 11th USA/Europe Air Traffic Management Research and Development Seminar (ATM 2015), Lisbon, Portugal, 16 September 2015. [Google Scholar]
- Montlaur, A.; Delgado, L. Flight and passenger delay assignment optimization strategies. Trans. Res. Part C Emerg. Technol. 2017, 81, 99–117. [Google Scholar] [CrossRef]
- Delgado, L.; Prats, X. Operating cost based cruise speed reduction for ground delay programs: Effect of scope length. Trans. Res. Part C Emerg. Technol. 2014, 48, 437–452. [Google Scholar] [CrossRef] [Green Version]
- Buxi, G.; Hansen, M. Generating day-of-operation probabilistic capacity scenarios from weather forecasts. Trans. Res. Part C Emerg. Technol. 2013, 33, 153–166. [Google Scholar] [CrossRef] [Green Version]
- EUROCONTROL. Algorithm to Describe Weather Conditions at European Airports; Technical Report; Eurocontrol: Brussels, Belgium, 2011. [Google Scholar]
- Fraport, A.G. Annual Report; Technical Report; Fraport AG: Frankfurt, Germany, 2013. [Google Scholar]
- Federal Aviation Administration. Advisory Circular 00-45—Aviation Weather Services; Technical Report; Federal Aviation Administration: Washington, DC, USA, 2016. [Google Scholar]
- O’Flynn, S. Airport Capacity Assessment Methodology—ACAM Manual; Technical Report 1.1; EUROCONTROL: Brussels, Belgium, 2016. [Google Scholar]
- Schultz, M.; Fricke, H. Managing Passenger Handling at Airport Terminal. In Proceedings of the 9th USA/Europe Air Traffic Management Research and Development Seminar (ATM 2011), Berlin, Germany, 14–17 June 2011. [Google Scholar]
- Röhner, P. Modelling of punctuality at Frankfurt Airport. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 2009. [Google Scholar]
- Fricke, H.; Schultz, M. Delay Impacts onto Turnaround Performance. In Proceedings of the 8th USA/Europe Air Traffic Management Research and Development Seminar (ATM 2009), Napa, CA, USA, 23–26 June 2009. [Google Scholar]
- Tadikamalla, P.R. A look at the Burr and related distributions. Int. Stat. Rev. 1980, 48, 337–344. [Google Scholar] [CrossRef]
- SESAR Joint Undertaking. E.02.35-ComplexityCosts-D3.2—Scenario Definition; Technical Report; University of Westminster: London, UK, 2015. [Google Scholar]
- Papadopoulos, A.S. The Burr distribution as a failure model from a Bayesian approach. IEEE Trans. Reliab. 1978, R-27, 369–371. [Google Scholar] [CrossRef]
- Lindsay, S.R.; Wood, G.R.; Woollons, R.C. Modelling the diameter distribution of forest stands using the Burr distribution. J. Appl. Stat. 1996, 23, 609–620. [Google Scholar] [CrossRef]














| Date | Airport (IATA) | Arrival/ Departure | Aircraft | Flight ID | Scheduled Time (min) | Actual Time (min) | Delay (min) | ||
|---|---|---|---|---|---|---|---|---|---|
| From | To | Arrival | Departure | ||||||
| 2013-03-13 | FRA | PMI | departure | 320 | AB9872 | 395 | 750 | 359 | 355 |
| 2013-03-13 | FRA | TXL | departure | 320 | AB6552 | 395 | −32,000 | −32,000 | −32,000 |
| 2013-03-13 | FRA | BRU | departure | 319 | LH1004 | 400 | 443 | 72 | 43 |
| 2013-03-13 | FRA | ZRH | departure | 319 | LH1182 | 400 | 411 | 49 | 11 |
| 2013-03-13 | FRA | TXL | departure | 321 | LH170 | 405 | 441 | 126 | 36 |
| 2013-03-13 | FRA | LCY | departure | E90 | CL926 | 405 | 447 | 82 | 42 |
| 2013-03-13 | CAI | FRA | arrival | 321 | LH581 | 405 | 394 | −11 | −31,000 |
| 2013-03-13 | FRA | PMI | departure | 738 | AB3328 | 410 | 459 | 118 | 49 |
| 2013-03-13 | FRA | BRE | departure | CR7 | CL34 | 410 | 436 | 32 | 26 |
| 2013-03-13 | STR | FRA | arrival | 319 | LH127 | 415 | 441 | 26 | −31,000 |
| Parameter | Measurement | METAR Code (Example) |
|---|---|---|
| wind | direction azimuth in degrees/speed [kn] | 06010KT |
| visibility | horizontal visibility [m] | 7000 |
| precipitation | significant weather phenomenon | −SN |
| cloud | cover/hight ∗ 100 [ft] above aerodrome level | BKN019 |
| temperature | air/dew point [C] | M03/M06 |
| pressure | Sea-level pressure (QNH) [hPa] | Q0998 |
| (TAF) | (NOSIG) |
| Weather Class | Description | Meteorological Conditions | Coefficient |
|---|---|---|---|
| (1) ceiling and visibility | deterioration of visibility (from “non-precision approach” up to “low visibility”) | precision approach runways: CAT I-III | max. 5 |
| (2) wind | strong head-/cross-wind, also gusts. | Wind speed > 16 knots (+gusts) | max. 4 (+1) |
| (3) precipitations | Runway friction influencing runway occupancy times. Complex procedures for runway clearing. | e.g., rain, (+/−) snow, frozen rain | max. 3 |
| (4) freezing conditions | Reduced runway friction, de-icing: additional taxi out times. | T ≤ 3 C, visible moisture or not, any precipitation. | max. 4 |
| (5) dangerous phenomena | Dangerous for aircraft, unsafe operations, unpredictable impact. | towering cumulus (TCU)/ cumulonimbus (CB), cloud cover, (+/−) shower. | 3–24 |
| (+/−) phenomena (e.g., thunderstorm) | 18–24 |
| Weather | (1) | (2) | (3) | (4) | (5) | ATMAP |
|---|---|---|---|---|---|---|
| Class | Visibility | Wind | Precipitation | Freezing | Dangerous | Score |
| METAR (Frankfurt) | EDDF 241320Z 03007KT 9999 −SN FEW012 SCT018 BKN025 01/M02 Q1013 R07L/295 R07C/295 R07R/295 R18/5//295 NOSIG | |||||
| measurement | 9999 | 03007KT | −SN | 01, −SN | - | (sum) |
| coefficient | 0 | 0 | 2 | 3 | 0 | 5 |
| METAR (Munich) | EDDM 082120Z 25006KT 3200 SHSN FEW005 SCT018CB BKN025 M00/M03 Q1015 TEMPO... | |||||
| measurement | 3200 | 25006KT | SHSN | M00, SHSN | SCT018CB, SH | (sum) |
| coefficient | 0 | 0 | 3 | 4 | 15 | 22 |
| Date | ATMAP | (1) | (2) | (3) | (4) | (5) | Cancellation Rates | |
|---|---|---|---|---|---|---|---|---|
| Score | Visibility | Wind | Precipitation | Freezing | Dangerous | Arrival | Departure | |
| 27 November 2013 | 4.72 | 1.87 | 0.00 | 0.83 | 2.02 | 0.00 | 2% | 2% |
| 12 March 2013 | 4.83 | 0.45 | 0.12 | 2.47 | 1.77 | 0.00 | 58% | 64% |
| IFR (Instrument Flight Rules) Annual Departure Movements | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ≤50,000 | [50,000, 100,000] | >100,000 | |||||||||
| c | k | c | k | c | k | ||||||
| Daily Average ATMAP Score | 0 | Arrival | 50.44 | 8.32 | 0.73 | 50.10 | 7.35 | 0.76 | 48.59 | 8.22 | 0.64 |
| 1 | 50.70 | 9.00 | 0.62 | 51.34 | 7.24 | 0.73 | 49.92 | 8.14 | 0.61 | ||
| 2 | 50.85 | 8.98 | 0.56 | 50.01 | 8.01 | 0.61 | 50.09 | 8.02 | 0.56 | ||
| 3 | 50.03 | 10.56 | 0.42 | 50.36 | 7.40 | 0.59 | 47.75 | 8.92 | 0.41 | ||
| 4 | 48.58 | 14.68 | 0.26 | 52.13 | 7.81 | 0.63 | 50.74 | 7.56 | 0.50 | ||
| 5 | 50.18 | 25.38 | 0.12 | 54.96 | 6.63 | 0.71 | 50.35 | 7.85 | 0.41 | ||
| ≥6 | no data | 54.68 | 7.29 | 0.53 | 65.06 | 5.22 | 0.71 | ||||
| 0 | Departure | 51.75 | 21.23 | 0.29 | 52.04 | 63.42 | 0.10 | 53.01 | 23.94 | 0.24 | |
| 1 | 51.69 | 21.19 | 0.25 | 52.37 | 58.19 | 0.10 | 52.82 | 26.67 | 0.19 | ||
| 2 | 51.93 | 52.09 | 0.10 | 51.38 | 26.04 | 0.18 | 52.38 | 35.20 | 0.13 | ||
| 3 | 52.42 | 28.69 | 0.15 | 52.42 | 21.63 | 0.19 | 52.98 | 29.14 | 0.14 | ||
| 4 | 54.59 | 13.86 | 0.28 | 55.40 | 13.53 | 0.34 | 53.41 | 21.52 | 0.15 | ||
| 5 | 54.92 | 31.57 | 0.10 | 52.43 | 18.58 | 0.18 | 56.05 | 15.26 | 0.24 | ||
| ≥6 | no data | 54.15 | 14.46 | 0.20 | 61.37 | 13.00 | 0.23 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schultz, M.; Lorenz, S.; Schmitz, R.; Delgado, L. Weather Impact on Airport Performance. Aerospace 2018, 5, 109. https://doi.org/10.3390/aerospace5040109
Schultz M, Lorenz S, Schmitz R, Delgado L. Weather Impact on Airport Performance. Aerospace. 2018; 5(4):109. https://doi.org/10.3390/aerospace5040109
Chicago/Turabian StyleSchultz, Michael, Sandro Lorenz, Reinhard Schmitz, and Luis Delgado. 2018. "Weather Impact on Airport Performance" Aerospace 5, no. 4: 109. https://doi.org/10.3390/aerospace5040109
APA StyleSchultz, M., Lorenz, S., Schmitz, R., & Delgado, L. (2018). Weather Impact on Airport Performance. Aerospace, 5(4), 109. https://doi.org/10.3390/aerospace5040109