Mutual Aerodynamic Interference Mechanism Analysis of an “X” Configuration Quadcopter
Abstract
:1. Introduction
2. Analysis Methods
2.1. Model Simplification
2.2. Definition of Nondimensionlized Aerodyamic Forces
2.3. Simulation Conditions
2.4. Computational Fluid Dynamics (CFD) Setup
2.4.1. Computational Domain
2.4.2. Grid Sensitivity Independence Verification and Time Step Verification
2.5. Virtual Modes Method
3. Mutual Interaction Mechanism Analysis
3.1. Hovering Condition
3.1.1. Aerodynamic Characteristics of Isolated Rotor
3.1.2. Mutual Interference Mechanism Analysis
3.2. 10 m/s forward Flight Conditionfigure
3.2.1. Aerodynamic Characteristics of Isolated Rotor
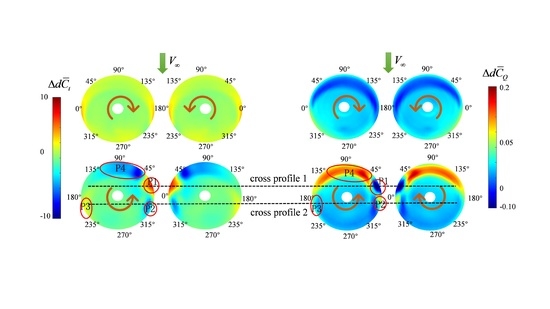
3.2.2. Interference Mechanism Analysis of Rotors
3.2.3. Interference Mechanism Analysis of the Fuselage
3.3. 25 m/s forward Flight Condition
3.3.1. Analysis of Aerodynamic Characteristics of Isolated Rotor
3.3.2. Interference Mechanism Analysis of the Rotors
3.3.3. Interference Mechanism Analysis of the Fuselage
4. Performance Analysis
4.1. Performance Analysis of Front Rotor
4.2. Performance Analysis of Rear Rotor
4.3. Performance Analysis of Fuselage
4.4. Summary of Performance Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Amezquita-Brooks, L.; Liceaga-Castro, E.; Gonzalez-Sanchez, M.; Garcia-Salazar, O.; Martinez-Vazquez, D. Towards a standard design model for quad-rotors: A review of current models, their accuracy and a novel simplified model. Prog. Aerosp. Sci. 2017, 95, 1–23. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Yu, L.; Mori, K. Aerodynamic characteristics of quadrotor helicopter. In Proceedings of the AIAA Flight Testing Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Khan, W.; Nahon, M. Toward an Accurate Physics-Based UAV Thruster Model. IEEE/ASME Trans. Mechatron. 2013, 18, 1269–1279. [Google Scholar] [CrossRef]
- Shastry, A.K.; Kothari, M.; Abhishek, A. Generalized Flight Dynamic Model of Quadrotor Using Hybrid Blade Element Momentum Theory. J. Aircr. 2018, 55, 2162–2168. [Google Scholar] [CrossRef]
- Theys, B.; Dimitriadis, G.; Hendrick, P.; De Schutter, J. Experimental and Numerical Study of Micro-Aerial-Vehicle Propeller Performance in Oblique Flow. J. Aircr. 2017, 54, 1076–1084. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, H. Aerodynamic Performance of a Quadrotor MAV Considering the Horizontal Wind. IEEE Access 2020, 8, 109421–109428. [Google Scholar] [CrossRef]
- Kolaei, A.; Barcelos, D.; Bramesfeld, G. Experimental Analysis of a Small-Scale Rotor at Various Inflow Angles. Int. J. Aerosp. Eng. 2018, 2018, 2560370. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.; Wang, J.; He, S.; Song, T. Rotor performance analysis and modeling of multirotor using wind-tunnel test. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020. [Google Scholar]
- Bannwarth, J.X.J.; Jeremy Chen, Z.; Stol, K.A.; MacDonald, B.A.; Richards, P.J. Aerodynamic Force Modeling of Multirotor Unmanned Aerial Vehicles. AIAA J. 2019, 57, 1250–1259. [Google Scholar] [CrossRef]
- Amezquita-Brooks, L.; Hernandez-Alcantara, D.; Santana-Delgado, C.; Covarrubias-Fabela, R.; Garcia-Salazar, O.; Ramirez-Mendoza, A.M.E. Improved model for micro-UAV propulsion systems: Characterization and applications. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2174–2197. [Google Scholar] [CrossRef]
- Chen, R.; Yuan, Y.; Thomson, D. A review of mathematical modelling techniques for advanced rotorcraft configurations. Prog. Aerosp. Sci. 2021, 120, 100681. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Jung, M.K.; Kwon, O.J. Numerical Study of Aerodynamic Performance of a Multirotor Unmanned-Aerial-Vehicle Configuration. J. Aircr. 2015, 52, 839–846. [Google Scholar] [CrossRef]
- Misiorowski, M.; Gandhi, F.; Oberai, A.A. Computational Study on Rotor Interactional Effects for a Quadcopter in Edgewise Flight. AIAA J. 2019, 57, 5309–5319. [Google Scholar] [CrossRef] [Green Version]
- Barcelos, D.; Kolaei, A.; Bramesfeld, G. Aerodynamic Interactions of Quadrotor Configurations. J. Aircr. 2020, 57, 1074–1090. [Google Scholar] [CrossRef]
- T-MOTOR-Polymer Folding/MF. Available online: https://store.tmotor.com/goods.php?id=741 (accessed on 6 October 2021).
- Niemiec, R.; Gandhi, F. Effects of inflow model on simulated aeromechanics of a quadrotor helicopter. In Proceedings of the 72nd Annual Forum of the American Helicopter Society, West Palm Beach, FL, USA, 17–19 May 2016. [Google Scholar]













































| Condition No. | Speed (m/s) | Pitch Angle (°) | RPM of Front Rotor (rad/s) | RPM of Rear Rotor (rad/s) |
|---|---|---|---|---|
| a | 0 | 0.00 | 331.60 | 331.60 |
| b | 5 | −2.76 | 321.57 | 341.81 |
| c | 10 | −7.02 | 316.45 | 356.38 |
| d | 15 | −13.07 | 330.66 | 386.86 |
| e | 20 | −21.60 | 395.63 | 460.70 |
| f | 25 | −33.37 | 556.15 | 620.24 |
| Cells | Difference | Difference | ||
|---|---|---|---|---|
| 5 M | 0.0160 | 24% | 0.035 | 12.9% |
| 10 M | 0.0135 | 4.6% | 0.032 | 3.2% |
| 15 M | 0.0129 | -- | 0.031 | -- |
| Iteration Step | ||
|---|---|---|
| 0.0329 | 0.0035 | |
| 0.0324 | 0.0034 | |
| 0.0283 | 0.0031 |
| VMs | Combination | Number of Grids |
|---|---|---|
| A | Whole UAV | 10.37 M |
| B | Front Rotor + Fuselage | 6.79 M |
| C | Rear Rotor + Fuselage | 6.78 M |
| D | Front Rotor + Rear Rotor | 8.83 M |
| E | Isolated Rotor | 4.57 M |
| F | Isolated Fuselage | 1.36 M |
| G | Two Rear Rotors | 8.86 M |
| 0.002308 | 0.02029 | 0.002308 | |
| 712.2 | 712.2 | 712.2 | |
| 0.8705 | 2.269 | 0.8705 | |
| 0.001886 | 0.006024 | 0.001886 | |
| 633.1 | 633.1 | 633.1 | |
| −0.6846 | 3.088 | −0.6846 | |
| 0.00106 | 0.007635 | 0.00106 | |
| 1424 | 1424 | 1424 | |
| 2.801 | 3.064 | 2.801 | |
| 0.0007351 | 0.002984 | 0.0007351 | |
| 1266.2 | 1266.2 | 1266.2 | |
| 1.578 | −2.33 | 1.578 | |
| 0.0118 | 0.0291 | −6.2602 × 10‒4 |
| 0.003386 | 0.005854 | 0.0005346 | |
| 1241 | 1241 | 1241 | |
| −1.997 | 0.5062 | −2.171 | |
| 0.000649 | 0.002034 | 0.0001888 | |
| 2481 | 2481 | 2481 | |
| −2.572 | −0.3932 | 3.229 | |
| 0.001352 | 0.0009802 | 0.0001064 | |
| 1116 | 1116 | 1116 | |
| −2.558 | 0.4408 | 1.01 | |
| 0.0005038 | 0.0007208 | 6.744e-5 | |
| 2233 | 3722 | 3722 | |
| −2.787 | −1.141 | 2.266 | |
| 0.0322 | −0.0209 | −0.0025 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Wang, J.; Lv, P. Mutual Aerodynamic Interference Mechanism Analysis of an “X” Configuration Quadcopter. Aerospace 2021, 8, 349. https://doi.org/10.3390/aerospace8110349
Ye J, Wang J, Lv P. Mutual Aerodynamic Interference Mechanism Analysis of an “X” Configuration Quadcopter. Aerospace. 2021; 8(11):349. https://doi.org/10.3390/aerospace8110349
Chicago/Turabian StyleYe, Jianchuan, Jiang Wang, and Peijian Lv. 2021. "Mutual Aerodynamic Interference Mechanism Analysis of an “X” Configuration Quadcopter" Aerospace 8, no. 11: 349. https://doi.org/10.3390/aerospace8110349
APA StyleYe, J., Wang, J., & Lv, P. (2021). Mutual Aerodynamic Interference Mechanism Analysis of an “X” Configuration Quadcopter. Aerospace, 8(11), 349. https://doi.org/10.3390/aerospace8110349