Experimental and Numerical Study on the Influence of Rubbing Force on Radial Crack Initiation in Labyrinth Seal Fins
Abstract
:1. Introduction
2. Experimental Study
2.1. Experimental System and Test Pieces
2.2. Experimental Parameters
2.3. Experimental Results
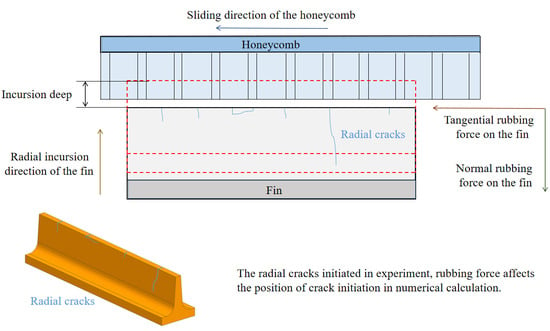
2.3.1. Morphology and Cracks after Rubbing
2.3.2. Influence of Rubbing Force on Rubbing Temperature
3. Numerical Study
3.1. Numerical Calculation Model
3.2. Results of Numerical Calculation
3.2.1. Influence of Rubbing Force on Crack Initiation
3.2.2. Influence of Rubbing Force on Stress
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- DeMasi-Marcin, J.T.; Gupta, D.K. Protective coatings in the gas turbine engine. Surf. Coat. Technol. 1994, 68–69, 1–9. [Google Scholar] [CrossRef]
- Chupp, R.E.; Hendricks, R.C.; Lattime, S.B.; Steinetz, B.M. Sealing in Turbomachinery. J. Propuls. Power 2006, 22, 313–349. [Google Scholar] [CrossRef]
- Draskovich, B.S.; Frani, N.E.; Joseph, S.S.; Narasimhan, D. Abrasive Tip/Abradable Shroud System and Method for Gas Turbine Compressor Clearance Control. U.S. Patent 5,704,759, 6 January 1998. [Google Scholar]
- Aslan-zada, F.E.; Mammadov, V.A.; Dohnal, F. Brush seals and labyrinth seals in gas turbine applications. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 216–230. [Google Scholar] [CrossRef]
- Schmid, R.K.; Ghasripoor, F.; Dorfman, M.; Wei, X. An Overview of Compressor Abradables. In Proceedings of the ITSC 2000, Dearborn, MI, 1–3 October 2000. [Google Scholar]
- Dai, X.; Yan, X. Effects of Labyrinth Fin Wear on Aerodynamic Performance of Turbine Stages: Part II—Mushrooming Damages. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Delebarre, C.; Wagner, V.; Paris, J.Y.; Dessein, G.; Denape, J.; Gurt-Santanach, J. An experimental study of the high speed interaction between a labyrinth seal and an abradable coating in a turbo-engine application. Wear 2014, 316, 109–118. [Google Scholar] [CrossRef] [Green Version]
- Bogdanovich, P.N.; Tkachuk, D.V. Thermal and thermomechanical phenomena in sliding contact. J. Frict. Wear 2009, 30, 153–163. [Google Scholar] [CrossRef]
- Rossmann, A. Die Sicherheit von Turbo-Flugtriebwerken, Band 2; Turbo Consult: Karlsfeld, Germany, 2000. [Google Scholar]
- Fischer, T.; Welzenbach, S.; Meier, F.; Werner, E.; kyzy, S.U.; Munz, O. Modeling the rubbing contact in honeycomb seals. Contin. Mech. Thermodyn. 2018, 30, 381–395. [Google Scholar] [CrossRef]
- Pychynski, T.; Dullenkopf, K.; Bauer, H.-J. Theoretical Study on the Origin of Radial Cracks in Labyrinth Seal Fins due to Rubbing. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Kennedy, F.E. Thermal and thermomechanical effects in dry sliding. Wear 1984, 100, 453–476. [Google Scholar] [CrossRef]
- Kennedy, F.E.; Karpe, S.A. Thermocracking of a mechanical face seal. Wear 1982, 79, 21–36. [Google Scholar] [CrossRef]
- Pychynski, T.; Höfler, C.; Bauer, H.-J. Experimental Study on the rubbing Contact Between a Labyrinth Seal Fin and a Honeycomb Stator. J. Eng. Gas Turbines Power 2015, 138, 062501. [Google Scholar] [CrossRef]
- Zhang, N.; Xuan, H.-J.; Guo, X.-J.; Guan, C.-P.; Hong, W.-R. Investigation of high-speed rubbing behavior of labyrinth-honeycomb seal for turbine engine application. J. Zhejiang Univ.-Sci. A 2016, 17, 947–960. [Google Scholar] [CrossRef]
- Rathmann, U.; Olmes, S.; Simeon, A. Sealing Technology: Rub Test Rig for Abrasive/Abradable Systems. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; pp. 223–228. [Google Scholar]
- Delebarre, C.; Wagner, V.; Paris, J.Y.; Dessein, G.; Denape, J.; Gurt-Santanach, J. Tribological characterization of a labyrinth-abradable interaction in a turbo engine application. Wear 2017, 370–371, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Thévenot, M.; Wagner, V.; Paris, J.Y.; Dessein, G.; Denape, J.; Harzallah, M.; Brunet, A.; Chantrait, T. Thermomechanical phenomena and wear flow mechanisms during high speed contact of abradable materials. Wear 2019, 426–427, 1102–1109. [Google Scholar] [CrossRef]
- Soler, D.; Saez De Buruaga, M.; Arrazola, P.J. Experimental investigation of contact forces and temperatures in rubbing interactions of honeycomb interstate seals. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1193, 012070. [Google Scholar] [CrossRef]
- Abaqus, SIMULIA User Assistance 2019. About Fracture Mechanics. Dassault Group. France. 2019. Available online: https://help.3ds.com/2019/english/DSSIMULIA_Established/SIMACAECAERefMap/simacae-m-EngXfem-sb.htm?ContextScope=all&id=0e4f47ecd3c44244afb58a118f76475f#Pg0 (accessed on 9 December 2020).
- Zhang, P.; Zhang, L.; Baxevanakis, K.P.; Zhao, L.G.; Bullough, C. Modelling short crack propagation in a single crystal nickel-based superalloy using crystal plasticity and XFEM. Int. J. Fatigue 2020, 136, 105594. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, L.; Jiang, R.; Bullough, C. Crystal plasticity finite-element modelling of cyclic deformation and crack initiation in a nickel-based single-crystal superalloy under low-cycle fatigue. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1769–1783. [Google Scholar] [CrossRef]
- Munz, O.; Schwitzke, C.; Bauer, H.J.; Welzenbach, S.; Kyzy, S.U. Modelling the Rubbing Process in Labyrinth Seals. In Proceedings of the Global Power & Propulsion Forum 2018, Zurich, Switzerland, 10–12 January 2018. [Google Scholar]
- Hühn, L.; Rieger, F.C.; Bleier, F.; Schwitzke, C.; Bauer, H.-J.; Behnisch, T. Extensive Investigations on Radial Crack Formation in Labyrinth Seals of Aircraft Engines. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Friedrichshafen, Germany, 4–6 September 2018; p. 8S. [Google Scholar]
- China Aeronautical Materials Handbook Committee. China Aeronautical Materials Handbook, Band 2; Standards Press of China: Beijing, China, 2002. (In Chinese) [Google Scholar]











| Composition | C | Cr | Ni | Co | W | Mo | Al | Ti | Fe |
|---|---|---|---|---|---|---|---|---|---|
| Content/% | 0.16 | 13.8 | balance | 9 | 4.0 | 3.8 | 3.1 | 4.8 | 0.32 |
| ρ/kg·m−3 | E/GPa | υ | α/10−6·°C−1 | cp/J·Kg−1·°C−1 | λ/W·m−1·°C−1 | σb/MPa | σp0.2/MPa | T/°C |
|---|---|---|---|---|---|---|---|---|
| 8160 | 199.0 | 0.3 | 12.56 | 402 | 12.12 | 1090 | 815 | 200 |
| 175.2 | 17.16 | 599 | 13.45 | 985 | 630 | 600 | ||
| 171.0 | 18.7 | 611 | 13.56 | 975 | 660 | 650 | ||
| 168.8 | 18.42 | 636 | 14.25 | 1000 | 610 | 700 | ||
| 165.8 | 20.10 | 643 | 14.17 | 1060 | 685 | 750 | ||
| 161.7 | 20.51 | 661 | 14.36 | 855 | 670 | 800 | ||
| 160.6 | 21.77 | 674 | 14.89 | 775 | 540 | 850 | ||
| 158.0 | 22.61 | 687 | 14.89 | 660 | 430 | 900 | ||
| 155.4 | 23.45 | 732 | 15.73 | 485 | 355 | 950 | ||
| 152.8 | 23.58 | 753 | 15.82 | 340 | 210 | 1000 | ||
| 150.2 | 24.27 | 775 | 16.68 | 213 | 138 | 1050 |
| Test No. | Sr (mm) | Vr (μm/s) | Rubbing Force (N) |
|---|---|---|---|
| C−1 | 0.1 | 20 | 35 |
| C−2 | 0.5 | 20 | 20 |
| C−3 | 50 | 25 | |
| C−4 | 80 | 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Chang, J.; Mi, Z.; Yang, W. Experimental and Numerical Study on the Influence of Rubbing Force on Radial Crack Initiation in Labyrinth Seal Fins. Aerospace 2022, 9, 831. https://doi.org/10.3390/aerospace9120831
Yang Y, Chang J, Mi Z, Yang W. Experimental and Numerical Study on the Influence of Rubbing Force on Radial Crack Initiation in Labyrinth Seal Fins. Aerospace. 2022; 9(12):831. https://doi.org/10.3390/aerospace9120831
Chicago/Turabian StyleYang, Yicheng, Jiaqi Chang, Zhaoguo Mi, and Weihua Yang. 2022. "Experimental and Numerical Study on the Influence of Rubbing Force on Radial Crack Initiation in Labyrinth Seal Fins" Aerospace 9, no. 12: 831. https://doi.org/10.3390/aerospace9120831
APA StyleYang, Y., Chang, J., Mi, Z., & Yang, W. (2022). Experimental and Numerical Study on the Influence of Rubbing Force on Radial Crack Initiation in Labyrinth Seal Fins. Aerospace, 9(12), 831. https://doi.org/10.3390/aerospace9120831