Contextual Augmentation Based on Metric-Guided Features for Ocular Axial Length Prediction
Abstract
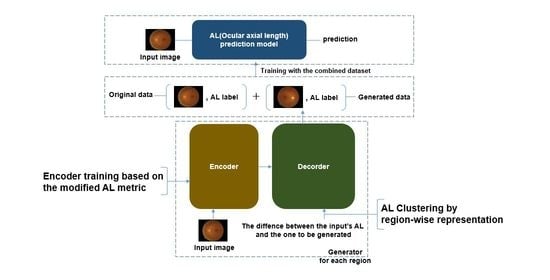
:1. Introduction
- The proposed framework confirms that the pairs of generated fundus images and AL can contribute to a reduction in the variance and bias of the prediction model, indicating that the generated pairs can provide regularization effects on the prediction networks.
- The independent training of the encoder in the proposed metric-based method and grouping of the latent feature vectors after the encoder are effective for generating valid data.
- Using the data set generated by the proposed method, improved AL prediction results can be obtained using the prediction models, even with fewer weights.
2. Related Work
2.1. Medical Image Synthesis
2.2. Augmentation
2.3. Metric Learning
3. Method
3.1. Neural Networks
3.1.1. Generator
- Encoder
- Feature vector modification
- Feature vector grouping
- Decoder
3.1.2. AL Predictor
3.2. The Procedure of the Data Augmentation
| Algorithm 1: Pseudo-code for the method. |
| Input: |
| Pairs for training encoder: (xenc,i, yenc,i) i = 1, 2 in the same region |
| Pairs for training generator: (xgen, ygen), (xgen,label, ygen,label) in different regions |
| Pairs for training AL prediction models: (xpred, ylabel) |
| Images for inference: xinf |
| Hyper-parameters for encoder |
| Output: |
| Predicted AL: O |
| Step 0: Dividing the data set according to a certain length of AL interval |
| Create an encoder and a generator for each region |
| Step 1: Training encoder for each region |
| Initialize weights of encoder |
| Set the hyperparameters for encoder |
| For the iteration number for the encoder do |
| Compute Enc1 = encoder(xenc,1) and |
| Enc2 = encoder(xenc,2) |
| Compute Lenc = Lenc(Enc1, Enc2, yenc,1, yenc,2) |
| Compute gradient genc = Lenc |
| Update weights wenc = SGD(genc) |
| End for |
| Save wenc |
| Step 2: Training the generator for each region |
| Initialize wgen |
| Replace the encoder weights with wenc in Step 1 |
| Stop updating the weights of the encoder |
| For the iteration number for the generator do |
| Compute Enc = encoder(xgen) in Generator |
| Create a random vector r |
| Compute ALdiff = ygen,1 − ygen,2 |
| Feature vector modification: Compute f″ with Enc, r, and ALdiff |
| Feature vector grouping according to Table 1 |
| Compute = Decoder(f″) |
| Compute Loss Lgen = MAE(xgenerated, xlabel) |
| Compute gradient ggen = Lgen |
| Update weights wgen = SGD(ggen) |
| End for |
| Save wgen |
| Step 3: Image combining |
| Set the number of images needed for each region |
| Calculate the number of generated images needed for each region |
| Generate the images and ALs with the generators |
| Combine the generated data sets with the original data set |
| Step 4: Training AL prediction models |
| Initialize wpred |
| For the iteration number for AL prediction models do |
| Compute results ypredicted = AL prediction models(xinf) |
| Compute Loss Lpred = MAE(ypredicted, ylabel) |
| Compute gradient gpred = Lpred |
| Update weights wpred = ADAM(gpred) |
| End For |
| Step 5: AL inference |
| Compute O = AL prediction model(xinf) |
4. Experiment
4.1. Data Set
4.2. Experimental Setup
Experiments
- Experiments on the effect of the different layer depth of the AL predictor
- Experiments on the feature vector modification
- Experiments on the independently trained encoder
4.3. Result
- Results of the generated pairs
- Results of the baselines
- Results of the Experiments on the feature grouping using end-to-end learning
- Results of the experiments on the independent training of the encoder
- Results of the experiments on the effect of the hype-parameter of the encoder
- Results of the experiments on the effect of the depth of the AL prediction models
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Emmert-Streib, F.; Yang, Z.; Feng, H.; Tripathi, S.; Dehmer, M. An Introductory review of deep learning for prediction models with big data. Front. Artif. Intell. 2020, 3, 4. [Google Scholar] [CrossRef] [Green Version]
- Zaman, K.S.; Reaz, M.B.I.; Ali, S.H.; Baker, A.A.A.; Chowdhury, M.E.H. Custom hardware architectures for deep learning on portable devices: A review. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6068–6088. [Google Scholar] [CrossRef] [PubMed]
- Raghavendra, U.; Fujita, H.; Bhandary, S.V.; Gudigar, A.; Hong, T.J.; Acharya, U.R. Deep convolution neural network for accurate diagnosis of glaucoma using digital fundus images. Inf. Sci. 2018, 441, 41–49. [Google Scholar] [CrossRef]
- Li, T.; Gao, Y.; Wang, K.; Guo, S.; Liu, H.; Kang, H. Diagnostic assessment of deep learning algorithms for diabetic retinopathy screening. Inf. Sci. 2019, 501, 511–522. [Google Scholar] [CrossRef]
- Saeed, F.; Hussain, M.; Aboalsamh, H.A.; Adel, F.A.; Owaifeer, A.M.A. Designing the Architecture of a Convolutional Neural Network Automatically for Diabetic Retinopathy Diagnosis. Mathematics 2023, 11, 307. [Google Scholar] [CrossRef]
- Tan, J.H.; Fujita, H.; Sivaprasad, S.; Bhandary, S.V.; Rao, A.K.; Chua, K.C.; Acharya, U.R. Automated segmentation of exudates, haemorrhages, microaneurysms using single convolutional neural network. Inf. Sci. 2017, 420, 66–76. [Google Scholar] [CrossRef]
- Raza, A.; Adnan, S.; Ishaq, M.; Kim, H.S.; Naqvi, R.A.; Lee, S. Assisting Glaucoma Screening Process Using Feature Excitation and Information Aggregation Techniques in Retinal Funds Images. Mathematics 2023, 11, 257. [Google Scholar] [CrossRef]
- Chen, C.; Chuah, J.H.; Ali, R.; Wang, Z. Retinal vessel segmentation using deep learning: A review. IEEE Access 2021, 9, 111985–112004. [Google Scholar] [CrossRef]
- Jin, G.; Chen, X.; Ying, L. Deep Multi-Task Learning for an Autoencoder-Regularized Semantic Segmentation of Fundus Retina Images. Mathematics 2022, 10, 4798. [Google Scholar] [CrossRef]
- Nadeem, M.W.; Goh, H.G.; Hussain, M.; Liew, S.; Andonovic, I.; Khan, M.A. Deep learning for diabetic retinopathy analysis: A review. research challenges, and future direction. Sensors 2022, 22, 6780. [Google Scholar] [CrossRef]
- Thompson, A.C.; Jammal, A.A.; Medeiros, F.A. A Deep learning algorithm to quantify neuroretinal rim loss from optic disc photographs. Am. J. Ophthalmol. 2019, 201, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Drexler, W.; Findl, O.; Menapace, R.; Rainer, G.; Vass, C.; Hitzenberger, C.K.; Fercher, A.F. Partial coherence interferometry: A novel approach to biometry in cataract surgery. Am. J. Ophthalmol. 1998, 126, 524–534. [Google Scholar] [CrossRef] [PubMed]
- Jeong, Y.; Lee, B.; Han, J.; Oh, J. Ocular axial length prediction based on visual interpretation of retinal fundus images via deep neural network. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 7200407. [Google Scholar] [CrossRef]
- Manivannan, N.; Leahy, C.; Covita, A.; Sha, P.; Mionchinski, S.; Yang, J.; Shi, Y.; Gregori, G.; Rosenfeld, P.; Durbin, M.K. Predicting axial length and refractive error by leveraging focus settings from widefield fundus images. Investig. Ophthalmol. Vis. Sci. 2020, 61, 63. [Google Scholar]
- Olsen, T. Calculation of intraocular lens power: A review. Acta Ophthalmol. 2007, 85, 472–485. [Google Scholar] [CrossRef]
- Haarman, A.E.G.; Enthoeven, J.W.L.; Tideman, J.W.L.; Tedja, M.S.; Verhoeven, V.J.M.; Klaver, C.C.W. The Complications of Myopia: A Reveiw and Meta-Analysis. Investig. Ophthalmol. Vis. Sci. 2020, 61, 49. [Google Scholar] [CrossRef]
- Oku, Y.; Oku, H.; Park, M.; Hayashi, K.; Takahashi, H.; Shouji, T.; Chihara, E. Long axial length as risk factor for normal tension glaucoma. Graefes Arch. Clin. Exp. Ophthalmol. 2009, 247, 781–787. [Google Scholar] [CrossRef]
- Moon, J.Y.; Garg, I.; Cui, Y.; Katz, R.; Zhu, Y.; Le, R.; Lu, Y.; Lu, E.S.; Ludwig, C.A.; Elze, T.; et al. Wide-field swept-source optical coherence tomography angiography in the assessment of retinal microvasculature and choroidal thickness in patients with myopia. Br. J. Ophthalmol. 2023, 107, 102–108. [Google Scholar] [CrossRef]
- Liu, M.; Wang, P.; Hu, X.; Zhu, C.; Yuan, Y.; Ke, B. Myopia-related stepwise and quadrant retinal microvascular alteration and its correlation with axial length. Eye 2021, 35, 2196–2205. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Jiang, H.; Yang, X.; Feng, L.; Hu, L.; Wang, L.; Lu, F.; Shen, M. Retinal Microvasculature Alteration in High Myopia. Investig. Ophthalmol. Vis. Sci. 2016, 57, 6020–6030. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing; Mcgraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data augmentation for deep learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef] [Green Version]
- Elasri, M.; Elharrouss, O.; Al-Maadeed, S.; Tairi, H. Image generation: A review. Neural Process Lett. 2022, 54, 4609–4646. [Google Scholar] [CrossRef]
- Wang, T.; Lei, Y.; Fu, Y.; Wynne, J.F.; Curran, W.J.; Liu, T.; Yang, X. A review on medical imaging synthesis using deep learning and its clinical applications. J. App. Clin. Med. Phys. 2021, 22, 11–36. [Google Scholar] [CrossRef] [PubMed]
- Dash, A.; Ye, J.; Wang, G. A review of Generative adversarial networks (GANs) and its applications in a wide variety of disciplines—From medical to Remote Sensing. arXiv 2021. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Yang, W.; Bi, F.; Yu, F.R. A State-of-the-art review on image synthesis with generative adversarial networks. IEEE Access 2020, 8, 63514–63537. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. arXiv 2015. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pabadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. arXiv 2014. [Google Scholar] [CrossRef]
- Hwang, D.; Kang, S.K.; Kim, K.Y.; Seo, S.; Paeng, J.C.; Lee, D.S.; Lee, J.S. Generation of PET attenuation map for whole-body time-of-flight 18F-FDG PET/MRI using a deep neural network trained with simultaneously reconstructed activity and attenuation maps. J. Nucl. Med. 2019, 60, 1183–1189. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Lee, J.; Kim, H.; Cho, B.; Cho, S. Deep-neural-network-based sinogram synthesis for sparse-view CT image reconstruction. IEEE Trans. Radiat. Plasma Med. Sci. 2019, 3, 109–119. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Ma, Y.; Capaldi, D.P.; Liu, J.; Zhao, W.; Du, J.; Xing, L. Incorporating prior knowledge via volumetric deep residual network to optimize the reconstruction of sparsely sampled MRI. Magn. Reson. Imaging 2020, 66, 93–103. [Google Scholar] [CrossRef]
- Chen, Y.; Long, J.; Guo, J. RF-GANs: A Method to Synthesize Retinal Fundus Images Based on Generative Adversarial Network. Comput. Intell. Neurosci. 2021, 2021, 3812865. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Dong, X.; Wang, T.; Higgins, K.; Liu, T.; Curran, W.J.; Mao, H.; Nye, J.A.; Yang, X. Whole-body PET estimation from low count statistics using cycle-consistent generative adversarial networks. Phys. Med. Biol. 2019, 64, 215017. [Google Scholar] [CrossRef] [PubMed]
- Mardani, M.; Gong, E.; Cheng, J.Y.; Vasanawala, S.; Zaharchuk, G.; Alley, M.; Thakur, N.; Han, S.; Dally, W.; Pauly, J.M.; et al. Deep generative adversarial networks for compressed sensing automates MRI. arXiv 2017. [Google Scholar] [CrossRef]
- Claro, M.L.; Veras, R.; Santana, A.M.; Vogado, L.H.S.; Junior, G.B.; Medeiros, F.; Tavares, J. Assessing the impact of data augmentation and a combination of CNNs on leukemia classification. Inf. Sci. 2022, 609, 1010–1029. [Google Scholar] [CrossRef]
- Li, D.; Du, C.; Wang, S.; Wang, H.; He, H. Multi-subject data augmentation for target subject semantic decoding with deep multi-view adversarial learning. Inf. Sci. 2021, 547, 1025–1044. [Google Scholar] [CrossRef]
- Huang, W.; Luo, M.; Liu, X.; Zhang, P.; Ding, H. Arterial spin labeling image synthesis from structural MRI using improved capsule-based networks. IEEE Access 2020, 8, 181137–181153. [Google Scholar] [CrossRef]
- Chen, F.; Wang, N.; Tang, J.; Liang, D. A negative transfer approach to person re-identification via domain augmentation. Inf. Sci. 2021, 549, 1–12. [Google Scholar] [CrossRef]
- Yan, M.; Hui, S.C.; Li, N. DML-PL: Deep metric learning based pseudo-labeling framework for class imbalanced semi-supervised learning. Inf. Sci. 2023, 626, 641–657. [Google Scholar] [CrossRef]
- Janarthan, S.; Thuseethan, S.; Rajasegarar, S.; Lyu, Q.; Zheng, Y.; Yearwood, J. Deep metric learning based citrus disease classification with sparse data. IEEE Access 2020, 8, 162588–162600. [Google Scholar] [CrossRef]
- Sundgaard, J.V.; Harte, J.; Bray, P.; Laugesen, S.; Kamide, Y.; Tanaka, C.; Paulsen, R.R.; Christensen, A.N. Deep metric learning for otitis media classification. Med. Image Anal. 2021, 71, 102034. [Google Scholar] [CrossRef]
- Sadeghi, H.; Raie, A. HistNet: Histogram-based convolutional neural network with chi-squared deep metric learning for facial expression recognition. Inf. Sci. 2022, 608, 472–488. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. arXiv 2015. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Hardt, M.; Recht, B.; Singer, Y. Train faster, generalize better: Stability of stochastic gradient descent. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, ICML, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Wilson, A.C.; Relogs, R.; Stern, M.; Srebro, N.; Recht, B. The marginal value of adaptive gradient methods in machine learning. In Proceedings of the 30th the Advances in Neural Information Processing System, NIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Kingma, D.P.; Welling, M. An introduction to variational autoencoders. arXiv 2019. [Google Scholar] [CrossRef]









| Region (mm) | Region (mm) | ||
|---|---|---|---|
| 20.5–21.0 | [,,0,0,0,0,0,0,0,0] | 30.0–30.5 | [,0,0,0,0,0,0,0,0,] |
| 21.0–21.5 | [,0,,0,0,0,0,0,0,0] | 30.5–31.0 | [0,,,0,0,0,0,0,0,0] |
| 21.5–22.0 | [,0,0,,0,0,0,0,0,0] | 31.0–31.5 | [0,,0,,0,0,0,0,0,0] |
| 27.5–28.0 | [,0,0,0,,0,0,0,0,0] | 31.5–32.0 | [0,,0,0,,0,0,0,0,0] |
| 28.0–28.5 | [,0,0,0,0,,0,0,0,0] | 32.0–32.5 | [0,,0,0,0,,0,0,0,0] |
| 28.5–29.0 | [,0,0,0,0,0,,0,0,0] | 32.5–33.0 | [0,,0,0,0,0,,0,0,0] |
| 29.0–29.5 | [,0,0,0,0,0,0,,0,0] | 33.0–33.5 | [0,,0,0,0,0,0,,0,0] |
| 29.5–30.0 | [,0,0,0,0,0,0,0,,0] | 34.5–35.0 | [0,,0,0,0,0,0,0,,0] |
| AL Prediction Model | MAE | Std |
|---|---|---|
| Base model | 10.23 | 2.56 |
| Deeper model | 5.49 | 1.43 |
| Use of Feature Vector Grouping | AL Prediction Model | |||
|---|---|---|---|---|
| Base Model | Deeper Model | |||
| MAE | Std | MAE | Std | |
| No | 8.32 | 6.92 | 5.32 | 1.21 |
| Yes | 4.29 | 0.43 | 4.38 | 0.97 |
| Use of Feature Vector Grouping | Encoder | AL Prediction Model | ||||
|---|---|---|---|---|---|---|
| Hyper- Parameters (a:0.01 and b:1) | Base Model | Deeper Model | ||||
| c | d | MAE | Std | MAE | Std | |
| No | 5 | 2 | 5.79 | 1.52 | 6.49 | 2.06 |
| 10 | 2 | 7.37 | 3.51 | 4.28 | 0.21 | |
| Yes | 5 | 2 | 3.96 | 0.23 | 4.33 | 0.25 |
| 10 | 2 | 4.09 | 0.16 | 4.08 | 0.12 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, Y.; Han, J.-H.; Oh, J. Contextual Augmentation Based on Metric-Guided Features for Ocular Axial Length Prediction. Mathematics 2023, 11, 3021. https://doi.org/10.3390/math11133021
Jeong Y, Han J-H, Oh J. Contextual Augmentation Based on Metric-Guided Features for Ocular Axial Length Prediction. Mathematics. 2023; 11(13):3021. https://doi.org/10.3390/math11133021
Chicago/Turabian StyleJeong, Yeonwoo, Jae-Ho Han, and Jaeryung Oh. 2023. "Contextual Augmentation Based on Metric-Guided Features for Ocular Axial Length Prediction" Mathematics 11, no. 13: 3021. https://doi.org/10.3390/math11133021
APA StyleJeong, Y., Han, J.-H., & Oh, J. (2023). Contextual Augmentation Based on Metric-Guided Features for Ocular Axial Length Prediction. Mathematics, 11(13), 3021. https://doi.org/10.3390/math11133021