Fire Risk Sub-Module Assessment under Solvency II. Calculating the Highest Risk Exposure

Abstract

The European Directive 2009/138 of Solvency II requires adopting a new approach based on risk, applying a standard formula as a market proxy in which the risk profile of insurers is fundamental. This study focuses on the fire risk sub-module, framed within the man-made catastrophe risk module, for which the regulations require the calculation of the highest concentration of risks that make up the portfolio of an insurance company within a radius of 200 m. However, the regulations do not indicate a specific methodology. This study proposes a procedure consisting of calculating the cluster with the highest risk and identifying this on a map. The results can be applied immediately by any insurance company, covered under the Solvency II regulations, to determine their maximum exposure to the catastrophic man-made risk of fire, instantly providing them with the necessary input for calibration of the solvency capital requirement.

1. Introduction

The management of an insurance company is based on its capacity, present, and future, to meet its commitments. The randomness of the phenomena to which an insurance company is exposed implies the development of probabilistic models of a stochastic nature for the correct valuation of the phenomena insured. However, traditional rating procedures do not work for catastrophic risks due to the usually very low frequency of loss events. These risks are the ones that the current legislation and the new European regulatory framework [1] known as Solvency II, whose principles revolve around the concept of solvency, try to capture. The Directive is structured around three pillars closely linked to each other and very similar to those harmonized by the banking sector in Basel II/III: risk-based capital requirements (Pillar I), enhanced governance (Pillar II), and increased transparency (Pillar III).

The primary objective of solvency capital requirements is to ensure an optimal capital level that allows insurance companies to face unforeseen losses while ensuring policyholders’ protection. This paper proposes a methodology that allows the calculation of solvency capital related to fires’ concentration risk, framed in man-made risk catastrophe of non-life underwritten insurance.

This risk requires a geospatial analysis of the set of risks based on the highest sum insured in the portfolio and where coverage includes fire or explosion and terrorist attacks. Thus, the regulations establish that every insurance company must geolocate the risks that it has insured in its portfolio to identify those partially or fully located within a 200-m radius of the highest concentration of risk [2] (pp. 85–86). However, this regulation, which is mandatory at the European level, does not specify how the cluster of sums insured are calculated. In the absence of a reference methodology, it is common for insurance companies to outsource the calculation of this sub-module, trying in some way to avoid possible future liabilities derived from a poor calibration of a risk of this type.

The paper is structured as follows. Section 2 relates the capital requirements called for by Solvency II with the capital requirements of the non-life catastrophe risk and the man-made catastrophe risk sub-module. Section 3 presents the proposed methodology for determining the highest concentration of risk for an insurance company. Section 4 demonstrates the methodology´s implementation on a portfolio whose risks have been simulated, and then, the outcomes are discussed. The paper ends with the conclusions.

2. Solvency II

The approval of the European Solvency II Directive 2009/138 was a step forward in revising the previous rules for the valuation of the financial situation of insurance companies, adopting a risk-based approach. Under this new paradigm, insurance companies’ valuation rules are thoroughly reviewed, reflecting a better measurement and management of all the risks to which they are exposed.

Solvency II’s fundamental essence is the establishment of the risk-based capital requirements, including an appropriate capital assessment as a guarantor of policyholder protection. The quantitative requirements applicable to insurance and reinsurance companies, which constitute Pillar I of the Solvency II regime, are based on an economic approach centered on the overall balance sheet. The available financial resources must cover the overall financial requirements. Thus, the solvency capital requirements’ fundamental objective is to ensure an optimum level of capital to enable insurance companies to cope with unforeseen losses while guaranteeing the protection of policyholders. Two types of solvency levels are established: an upper limit, called SCR (Solvency Capital Requirement), and a lower limit called MCR (Minimum Capital Requirement), which determines the minimum level of security or absolute minimum amount of capital below which an entity could not continue to operate [1,2].

For its calculation, a general method is established based on a standard formula that adopts a modular approach to risk aggregation. However, the Directive also establishes that under certain prerequisites and authorization by the supervisory body, the SCR can be obtained by means of an internal model or calibration of specific parameters.

Solvency II establishes that the SCR is calculated considering the effects of diversification, with the regulator assuming that VaR (Value At Risk) is a measure that complies with the subadditivity axiom. It could be thought that the model proposed in the Directive, the standard model, is based on multivariate normality assumptions regarding the random variables representing risks.

The capital requirement for non-life underwriting risk is calculated taking into account the possible combinations and correlations of the following risk groups [2] (pp. 72–87): non-life premium and reserve, non-life catastrophe, and non-life lapse. More specifically, the non-life catastrophe risk sub-module (SCR_nlCAT) consists of all of the following sub-modules: the natural catastrophe risk sub-module (SCR_natCAT), non-proportional property reinsurance catastrophe risk (SCR_nppropperty) sub-module, the man-made catastrophe risk sub-module (SCR_mmCAT), and the sub-module for another non-life catastrophe risk (SCR_CATother), as shown in the following expression [2] (pp. 75–76):

$$SC{R}_{\mathrm{nlCAT}}=\sqrt{{(SC{R}_{\mathrm{natCAT}}+SC{R}_{\mathrm{nppropperty}})}^2+SC{R}^2{}_{\mathrm{mmCAT}}+SC{R}^2{}_{\mathrm{CATother}}}$$

(1)

2.1. Man-Made Catastrophe Risk

There are risks that, although they can be classified as catastrophic, are not due to natural phenomena, but are caused by man or by anthropogenic effects. In contrast to the former, these types of risks affect a very specific location, with a significant degree of severity in the case of an extreme event. Figure 1 shows the evolution of catastrophic events that occurred between 1970 and 2018. There were 304 catastrophe events in 2018, and 123 were man-made disasters.

Catastrophic risks arise from extreme or irregular events that are not sufficiently reflected by the mandatory capital of the risk of premiums and reserves. These include risks of natural catastrophes, catastrophic risks in non-proportional reinsurance of property damage, risk of catastrophes caused by man, as well as other catastrophic risks in non-life insurance.

In Spain’s case, given the particularities due to the Insurance Consortium’s protection, an insurance company’s capital requirements will be lower than that of other European countries’ capital requirements. In this sense, the Spanish Insurance Consortium is a unique entity in Europe. In relation to catastrophic risks, its purpose is to indemnify the losses arising from extraordinary events occurring in Spain and affect risks located therein. For these purposes, direct damage to persons and property will be considered, as well as the loss of profits as a consequence thereof. For the risk in question, only those caused violently due to terrorism, rebellion, sedition, riot, and civil commotion will be considered.

However, the Consortium’s consideration as a risk mitigator has not been taken into account when considering the impact in terms of solvency capital requirements in this work. The Spanish Insurance Consortium would only cover a part of the fire risks (related to terrorism), leaving aside other risks subject to this sub-module and on the other hand, considering the standard formula and simplified calculations emanate from a European Directive of obligatory compliance for the different member states.

This paper focuses on the risk of man-made disasters where capital requirement must be calibrated at 99.5% of VaR. Unlike natural catastrophes, where the gross sum insured would be divided among competitors in the insurance market, man-made catastrophic events can only harm one insurer, since the impact is felt in a single location (or by a single policyholder) and its surroundings, with the damage being very concentrated and of a greater severity.

Thus, for the man-made catastrophic risk module, the following risk sub-modules described in the Solvency II Directive regulations must be considered, as well as the corresponding transposition into the legal system of each country: (a) the motor vehicle liability risk sub-module, (b) the marine risk sub-module, (c) the aviation risk sub-module, (d) the fire risk sub-module. (e) the liability risk sub-module, and (f) the credit and suretyship risk sub-module. The capital requirement for the man-made catastrophe risk is equal to the following [2] (pp. 83–84):

$$SC{R}_{mmCAT}=\sqrt{{\displaystyle \sum }_{i}SC{R}_i^2}$$

(2)

where the sum includes all sub-modules set out and SCR_i denotes the capital requirements for sub-module i.

Fire Risk Sub-Module

Until the advent of the Solvency II regulatory framework, the non-life fire sub-module was not considered, and there was limited knowledge of the protection of each policy by insurers. In this regard, to ensure that all insurance and reinsurance companies are on an equal footing when calculating the solvency capital requirement, a standard formula was determined with the sub-modules covering the different risks and the methods, assumptions, and general parameters to be used for its calculation. Within the underwriting risks, the weight of the catastrophe burden is very significant in the non-life module and has required the creation of specific working groups for its calibration.

Thus, the European legislator’s final approach is the unification of property damage and terrorism coverages through the more significant accumulation of risks reduced by the reinsurance program presented by each insurance company [2].

Fire risk solvency capital requires identifying the set of buildings with the highest concentration sum insured, concerning damages on each building due to fire or explosion, including as a result of terrorist attack. All buildings located, totally or partially, within a radius of 200 m [2] must be determined (pp. 85–86). This is a legal obligation and obligatory compliance, but there are no guidelines for calculating the accumulation of sums insured. Solvency II establishes that this risk must be calculated, but it leaves insurance companies free to carry out the calculation by adopting methodologies that better reflect the underlying risk.

The standard formula does not consider the real risk for the insurance companies according to the type of risks they contract for the calculation of the exposure based on the capital at risk. Any considered risk accumulation will be based on the aggregation of the total sums insured of all the policies subscribed within a radius of 200 m, regardless of the inherent activity they present.

This can be somewhat complicated since, although an accumulation of risks within a radius of 200 m may imply an expected loss, this risk may vary depending on the probability of the extreme event, the radius of impact and its severity, and the type of risks underwritten. The risk typology basis is vital because a severe claim in a location linked to an industrial location does not have the same impact as a home or business claim. The factors that lead to significant exposure to risk are different.

Likewise, under the Solvency II prism, insurance and reinsurance entities have the possibility of using a simplified calculation [1] in a standard formula environment if the nature, volume, and complexity of the risks justify it, under the principle of proportionality of the risks underlying the European Directive itself. In this regard, consideration (15) of the Commission Delegated Regulation (EU) 2019/981 [4] provides for the possibility for an insurance entity to restrict its process of identifying the highest concentration of fire risk to the environment of its most significant fire risk exposures, provided that such an approach is proportionate to the nature, scale, and complexity of the fire risk exposure of the insurance or reinsurance undertakings.

This alternative and simplified calculation approach does not invalidate the methodology proposed in this paper. Thus, the use of the simplified calculation should not lead to an incorrect calculation of the solvency capital requirement that could have a relevant influence on the decision making (as stated in the European Commission Delegated Regulation (EU) 2009/981 of 8 March 2009) after obtaining the highest sum insured per insured risk for industrial, commercial, and residential fire after mitigation of the reinsurance amounts. The calculation of the highest risk cluster within a radius of 200 m implies that it has to be calculated with the proposed methodology. Its calculation may or may not be limited only to the surroundings of the largest fire risk exposure, in which case, the calculation process would be significantly expedited since the number of insured risks included as input in the proposed model would be reduced, resulting in a reduction in the number of possible clusters of the highest risk and of the computation time.

From a simulated base of 1000 sums insured, this paper shows how to calculate the cluster containing the highest risk by geolocation of risks within a radius of 200 m of this point. The application is immediate and requires these calculations to be completed by all European insurance companies that emanate from the Solvency II regulatory framework. The principle of proportionality between entities based on their size and structure must prevail at all times. In this way, it is possible to establish specific reinsurance programs to mitigate solvency capital requirements and determine a risk management mechanism for possible adverse events of catastrophic nature.

3. Determination of the Highest Concentration of Risk for an Insurance Company

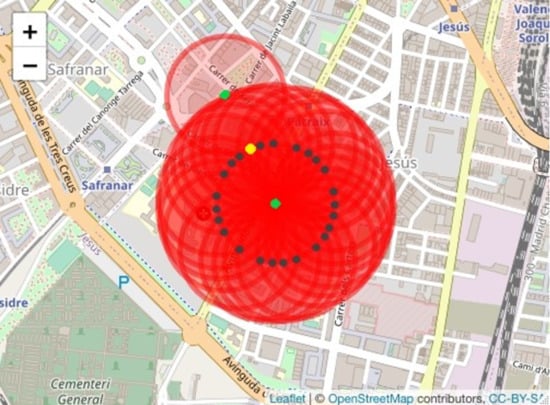
3.1. Methodology

For some years, the risk cluster concept has been used in the actuarial field, focusing predominantly on life and accident insurance [5,6,7,8]. In particular, it measures the sum of insured values liable to be affected by the same claim event. Thus, Solvency II requires calculating the capital requirement for fire risk to determine the set of buildings with the largest sum insured partly or fully located within a radius of 200 m [2] (pp. 85–86). However, the regulations do not indicate how to calculate this estimate. In this paper, we address this problem through the following steps:

Step 1. We calculate the distance between each pair of sums insured. This may seem straightforward, but calculating the distance between two geographical points located on the earth’s sphere (longitude and latitude) and not on a plane (Cartesian coordinates) is not so simple. One of the approximations most used in practical applications [9,10,11,12,13,14,15,16] to calculate the distance between two geographical points is the Haversine distance [17], which is given by:

$$dHaversine=2·r·arcsin\left(\sqrt{si{n}^2\left(\frac{{\phi }_2-{\phi }_1}{2}\right)+cos\left({\phi }_1\right)cos\left({\phi }_2\right)si{n}^2\left(\frac{{\lambda }_2-{\lambda }_1}{2}\right)}\right).$$

(3)

where ${\lambda }_1$ and ${\lambda }_2$ are the lengths of points 1 and 2 expressed in radians, respectively; ${\phi }_1$ and ${\phi }_2$ are the latitudes of points 1 and 2 expressed in radians, respectively, and r is the radius of the earth (the equatorial radius is 6378.137 km and the mean radius is 6371 km).

The Haversine distance assumes that the earth is spherical when it is slightly ellipsoidal. In this case, Vicenty distance [18] can be used. From the following notation:

$$\begin{gathered} a,b=major and minor semiaxes of the ellipsoid \\ f, flattening=\left(a-b\right)/a \\ {\phi }_1 and {\phi }_2=geodetic latitude \\ L=difference in longitude \\ {U}_1=\mathrm{atan}\left(1-f\right)-\tan \left({\phi }_1\right) \\ {U}_2=\mathrm{atan}\left(1-f\right)·\tan \left({\phi }_2\right) \\ L=\lambda \\ {\lambda }^{\prime }=2\pi , \end{gathered}$$

the algorithm to calculate the Vincenty distance iteratively evaluate equations from 4 to 12, while abs$\left(\lambda -{\lambda }^{\prime }\right)>{10}^{-12}$.

$$\mathit{sin}\left(\sigma \right)=\sqrt{{\left(\mathit{cos}\left(U_2\right)\mathit{sin}\left(\lambda \right)\right)}^2+{\left(\mathit{cos}\left(U_1\right)\mathit{sin}\left(U_2\right)-\mathit{sin}\left(U_1\right)\mathit{cos}\left(U_2\right)\mathit{cos}\left(\lambda \right)\right)}^2}$$

(4)

$$\mathit{cos}\left(\sigma \right)=\mathit{sin}\left(U_1\right)\mathit{sin}\left(U_2\right)+\mathit{cos}\left(U_1\right)\mathit{cos}\left(U_2\right)\mathit{cos}\left(\lambda \right)$$

(5)

$$\sigma =atan2\left(\mathit{sin}\left(\sigma \right),\mathit{cos}\left(\sigma \right)\right)$$

(6)

$$\mathit{sin}\left(\alpha \right)=\mathit{cos}\left(U_1\right)\mathit{cos}\left(U_2\right)\frac{\mathit{sin}\left(\lambda \right)}{\mathit{sin}\left(\alpha \right)}$$

(7)

$$co{s}^2\left(\alpha \right)=1-si{n}^2\left(\alpha \right)$$

(8)

$$\mathit{cos}\left(2\sigma m\right)=\mathit{cos}\left(\sigma \right)-\frac{2\mathit{sin}\left(U_1\right)\mathit{sin}\left(U_2\right)}{co{s}^2\left(\alpha \right)}$$

(9)

$$C=\frac{f}{16}co{s}^2\left(\alpha \right)\left[4+f\left(4-3co{s}^2\left(\alpha \right)\right)\right]$$

(10)

$${\lambda }^{\prime }=\lambda$$

(11)

$${\lambda }^{\prime }=L+\left(1-C\right)f sin\left(\alpha \right)\left\{\sigma +C sin\left(\alpha \right)\left[\mathit{cos}\left(2\sigma m\right)+C cos\left(\sigma \right)\left(-1+2{\mathit{cos}}^2\left(2\sigma m\right)\right)\right]\right\}.$$

(12)

Then, when $\lambda$ converges, the algoritm evaluates:

$$u^2=co{s}^2\left(\alpha \right)\frac{a^2-b^2}{a^2}$$

(13)

$$A=1+\frac{u^2}{\mathrm{16,384}}\left\{4096+u^2\left[-768+u^2\left(320-175u^2\right)\right]\right\}$$

(14)

$$B=\frac{u^2}{1024}\left\{256+u^2\left[-128+u^2\left(74-47u^2\right)\right]\right\}$$

(15)

$$\mathsf{\Delta }\sigma =Bsin\left(\sigma \right)\left\{\mathit{cos}\left(2\sigma m\right)+\frac{B}{4}\left[\mathit{cos}\left(\sigma \right)\left(-1+2{\mathit{cos}}^2\left(2\sigma m\right)-\frac{B}{6}\mathit{cos}\left(2\sigma m\right)\left(-3+4si{n}^2\left(\sigma \right)\right)\left(-3+4{\mathit{cos}}^2\left(2\sigma m\right)\right)\right)\right]\right\}.$$

(16)

Thus, the Vincenty distance between two points will be given by Equation (17):

$$dVincenty=bA\left(\sigma -\mathsf{\Delta }\sigma \right).$$

(17)

Although Vincenty distance is quoted as being highly accurate, it is an iterative process and computationally time consuming.

Alternatively, the longitudes and latitudes in decimal degrees can be converted to UTM (Universal Transverse Mercator) coordinate system. From cartesian coordinates, the Euclidean distance between two points can be calculated.

Step 2. We create two matrices (empty), one to record the distance between each pair of geographic points (distance matrix) and the other to record the sum insured by the insurance company if the distance between two policyholders is less than 200 m (risk matrix).

Step 3. The total sum insured is calculated from the risk matrix and considering each policyholder as the centroid of a risk cluster for each cluster. Next, the cluster (policyholders) that represents the highest concentration of risks is identified as well as the set of risks that are part of that cluster.

To work out the highest risk for the insurance company, we have written a function in R (cumulus.R) (a simplified and limited version of this function is found in Appendix C).

The cumulus.R function has 6 arguments. The first argument is the database of the insurance company´s policyholders, and it must be a dataframe or a tibble. The data must necessarily have four columns, in this order: (1) identification of the policyholder, (2) longitude, (3) latitude (in decimal degrees), and (4) total sum insured. If the Euclidean distance is used, it is necessary to calculate the Cartesian coordinates previously. In the dataset, the Cartesian coordinates are located in columns 7 and 8. The second argument (cumulus) refers to the number of clusters to be obtained. By default, the cumulus argument is prefixed to the value 1. The third argument refers to the distance within which the policyholders must be located to calculate the highest risk, i.e., radius. In accordance with the Solvency II Directive, the radius is pre-set at 200 m. The fourth argument (radius) is the additional margin of distance that we want to incorporate to counteract possible inaccuracies in distances’ estimates. Thus, an insurance company may consider it appropriate to extend the radius of the calculation of the highest risk, e.g., incorporating a margin of 20 m, meaning the calculation radius would actually reach 220 m. The fifth argument is extended. This argument takes the value 0 by default, but it must be set to the value 1 if a margin is indicated and if the highest accumulation of risk is maintained at a radius of 200 m or to the value 2 for a new cluster of greater risk when locating those policyholders in the new radius (radius + margin). Lastly, the sixth argument is the type of distance used (by default, the argument is set to the Haversine distance).

With respect to distances, although several R packages allow calculation of the Haversine distance between two geographic points (e.g., the package geosphere (2019) [19]), cumulus refers to the function as hav_distance (see Appendix A). hav_distance is a function that we have written to calculate the Haversine distance to reduce the calculation time. Specifically, with the geosphere distHaversine function, it takes an average of 4.39 min to obtain the matrix of distances between each pair of points. This time is reduced to 38.36 s with the hav_distance function. These average times have been obtained using an Intel Core i5-10210U computer, 1.60 GHz, and 8 GB of RAM. On the other hand, to calculate the Vincenty distance, we call the corresponding function in the geosphere package. This is because although Vincenty distance is quoted as being highly accurate, it is an iterative process and computationally time consuming. We only calculate the Vincenty distance for comparison results. In fact, since the distances that we really need to calculate are relatively small, the ellipsoidal effect of the earth is minimal, so the haversine and Euclidean distances (see Appendix B) are preferred.

In our study, the geographic area established for a cluster is centered on an insurance policy, whereas many clusters can be created as an entity insures policies. The geographical representation of the policies insured by points based on their geolocation coordinates allows evaluating risks over a short distance.

3.2. Dataset

To determine the highest risk cluster that an insurance company has to assume as a previous step for calculating the solvency capital requirement (SCR), we use a dataset of 1000 risks. The sums insured (column 4, in euros) in this dataset come from a random sample of policyholders from a real insurance company. However, their geographic locations (columns 2 and 3, longitude and latitude in decimal degrees) have been simulated in another city (specifically in Valencia, Spain) in order to preserve privacy. Data file (xlsx file) is supplied as the Supplementary Material with this article. The sum insured refers to the risk coverage of both the buildings and content. The distribution of the policyholders can be seen in Figure 2.

The main descriptive statistics of the sum insured are shown in

Table 1. Descriptives of the sum insured.

Statistic	Sum Insured (€)
Minimum	34,099.73
First quartile	194,856.66
Median	461,285.27
Third quartile	1,120,281.02
Mean	1,249,490.66
Maximum	12,388,953.79
Standard deviation	1,639,387.156

Source: compiled by the authors.

.

4. Case Study Results and Discussion

To obtain the highest risk for the insurance company, we have to execute the cumulus function, which returns a list of 6 elements as a result of the analysis:

• data: original dataframe to which a first column (ref) was added to list the policyholders consecutively.
• distance.matrix: matrix with the selected distance (Haversine by default) for each pair of geographic points.
• cumulus.matrix: risk matrix, in which each policyholder constitutes the centroid of a risk cluster.
• maximum.cumulus: amount of the highest risk for the insurance company.
• identification.cumulus: policyholder representing the centroid of the highest risk cluster.
• cumulus.data: dataframe made up of the policyholders who form the highest risk cluster.

We begin by analyzing the case in line with regulations: determination of the highest risk of the policyholders located within a radius of 200 m. To do this, we first load the function, source (“cumulus.R”) and then execute the instruction shown below. Note that Harversine distance is calculated by default.

result1 ← cumulus(data).

Depending on the computer, the estimated average execution time is 41.39 s. the main results, it should be noted that the highest risk for the insurance company amounts to 41,431,645 euros.

Table 2. The highest risk cluster for the insurance entity.

Ref	id	Longitude	Latitude	Sum.Insured	Highest.Sum.Insured	Insured.Cluster
231	2266	−0.3745403	39.4724532	3,603,539	41,431,645	29
899	2940	−0.3745509	39.4723678	1,467,116	41,242,621	29
405	667	−0.3743963	39.4721817	295,888	40,118,952	27
929	1552	−0.3748926	39.4713922	255,455	32,632,384	24
717	1394	−0.3743319	39.4718396	1,979,428	32,484,721	22
510	1517	−0.3751963	39.4735817	565,817	31,562,826	24
376	494	−0.3747399	39.4709996	117,543	30,211,509	22
635	685	−0.3748998	39.4724242	134,527	29,676,494	27
762	878	−0.3731713	39.4720993	372,652	29,629,749	24
228	3067	−0.3723715	39.4725479	3,608,698	28,545,751	17
72	3111	−0.3747591	39.4725809	552,030	28,406,181	26
890	2927	−0.3729262	39.4712578	9,610,409	27,250,428	20
213	1899	−0.3744403	39.4732532	154,923	26,992,852	22
984	2453	−0.3761294	39.472035	696,180	26,919,386	26
413	2998	−0.3760352	39.4727656	442,312	26,690,708	26
752	642	−0.3722713	39.4722993	130,279	26,005,069	17
365	524	−0.3764342	39.4721113	6,467,363	26,004,924	26
334	2656	−0.3739059	39.4738459	250,591	25,825,806	22
696	2640	−0.3739059	39.4738459	4,211,254	25,825,806	22
2	2511	−0.3767362	39.4720473	999,983	25,294,012	27
531	1831	−0.3750513	39.4736109	1,980,909	25,095,463	23
101	480	−0.3755984	39.4711045	104,032	23,984,461	25
855	2638	−0.3731927	39.4734223	829,238	23,877,075	21
537	2725	−0.3742187	39.4708188	1,265,507	23,729,718	19
120	2926	−0.3740933	39.4710726	91,244	23,719,724	19
790	2910	−0.373064	39.4737415	123,686	23,446,660	19
42	2985	−0.3758014	39.4715086	246,718	22,861,348	24
179	712	−0.3742403	39.4738532	191,377	22,659,420	22
641	1352	−0.372606	39.4733964	682,947	19,410,813	16

Source: compiled by the authors.

shows the results that cumulus provides for the highest risk cluster using the Haversine distance. Column 6 (highest.sum.insured), which is ordered in descending order, represents the highest risk considering each policyholder (id) as the centroid of a cluster. Policyholder 2266 represents the centroid of this risk cluster, which is made up of the remaining 28 policyholders listed in column 2. Column 7 (insured.cluster) represents the number of policyholders that make up each cluster.

The cluster with the highest risk (Table 2) was also identified on the map to ease interpreting the results by managing the insurance company [20] (see Figure 3). The policyholders that form the highest risk cluster appear as blue dots, while the rest of the policyholders appear as black dots. For each point, the Id of the policyholder and their sum insured are shown. A red marker identifies the centroid of the cluster.

With both the Vincenty distance and the Euclidean distance, we obtain the same results, which are slightly different from those obtained with the Haversine distance (see Table 2). Now, policyholder 2266 remains as the centroid of the highest risk cluster (Table 2), but policyholder 1960 is included and the highest risk amounts to 49,925,568 euros. However, the time consumed to obtain the results based on the Vincenty distance was 3.83 min and the Euclidean distance was 38.54 s.

Given that both the policyholders’ geolocation and the calculation of the distance between them are not accurate, the insurance company may decide to incorporate a margin of error to estimate the highest risk. Instead of considering all the policyholders located within a radius of 200 m, the insurer may consider the policyholders located within a radius of, e.g., 220 m. In this case, the margin of error assumed by the insurance company is 20 m. We have to consider the essential role of reinsurance programs in reducing capital charges in hypothetical adverse scenarios of high severity. The migration of reinsurance acts as a guarantor optimizing capital structure and the increase in risk transfers.

Under this assumption, the insurance company can consider two scenarios:

• Scenario 1. Maintain policyholder 2266 as the centroid of the highest risk cluster and extend the cluster radius by 20 m to identify the policyholders who are within the extended radius. The results of this scenario 1 using the Haversine distance are obtained by executing the following instruction:

result2 ← cumulus(data, margin = 20, extended = 1).

Figure 4 shows the original cluster (in gray) and the new risk cluster (in red); in both cases, the centroid of the cluster is policyholder 2266. By expanding the radius from 200 to 220 m, a total of 4 further policyholders are incorporated into the cluster: 1690, 2538, 2551, and 2593. Under this scenario 1, the highest risk for the insurance company amounts to 44,695,192 euros. The results obtained are the same when the Vincenty or Euclidean distances are used, while the biggest difference is in the time consumed in executing the cumulus function: Haversine (42.75 s), Euclidean (38.82 s), and Vincenty (3.85 min).

• Scenario 2. Determine a new risk cluster considering all the policyholders who are located in the new radius (200 m plus the margin of error). To obtain the results of this scenario, we execute the following instruction:

  result3 ← cumulus(data, margin = 20, extended = 2).

The results obtained are the same as that of the results obtained using all three distances and are shown in

Table 3. The highest risk cluster for the insurance entity. Scenario 2 (Haversine distance).

Ref	id	Longitude	Latitude	Sum.Insured	Highest.Sum.Insured	Insured.Cluster
405	667	−0.3743963	39.4721817	295,888	45,090,147	34
72	3111	−0.3747591	39.4725809	552,030	44,710,177	34
231	2266	−0.3745403	39.4724532	3,603,539	44,695,192	33
899	2940	−0.3745509	39.4723678	1,467,116	44,695,192	33
635	685	−0.3748998	39.4724242	134,527	44,214,279	33
717	1394	−0.3743319	39.4718396	1,979,428	40,521,606	30
510	1517	−0.3751963	39.4735817	565,817	37,391,765	29
213	1899	−0.3744403	39.4732532	154,923	36,989,629	30
531	1831	−0.3750513	39.4736109	1,980,909	34,662,865	27
762	878	−0.3731713	39.4720993	372,652	34,480,801	28
376	494	−0.3747399	39.4709996	117,543	33,791,787	26
228	3067	−0.3723715	39.4725479	3,608,698	33,223,488	26
929	1552	−0.3748926	39.4713922	255,455	33,064,176	27
413	2998	−0.3760352	39.4727656	442,312	32,482,616	31
502	2593	−0.3720783	39.472529	497,248	31,950,599	22
365	524	−0.3764342	39.4721113	6,467,363	30,998,182	35
984	2453	−0.3761294	39.472035	696,180	30,107,169	32
2	2511	−0.3767362	39.4720473	999,983	29,944,752	35
179	712	−0.3742403	39.4738532	191,377	29,548,613	27
39	2538	−0.376853	39.472	110,133	29,378,935	34
795	2551	−0.376853	39.472	2,162,243	29,378,935	34
752	642	−0.3722713	39.4722993	130,279	28,919,798	22
890	2927	−0.3729262	39.4712578	9,610,409	28,467,010	23
101	480	−0.3755984	39.4711045	104,032	27,151,364	27
334	2656	−0.3739059	39.4738459	250,591	27,138,018	25
696	2640	−0.3739059	39.4738459	4,211,254	27,138,018	25
855	2638	−0.3731927	39.4734223	829,238	25,856,503	22
537	2725	−0.3742187	39.4708188	1,265,507	25,856,380	23
42	2985	−0.3758014	39.4715086	246,718	25,804,871	26
120	2926	−0.3740933	39.4710726	91,244	25,108,207	22
242	1690	−0.3738458	39.4707353	493,923	24,698,915	21
790	2910	−0.373064	39.4737415	123,686	23,877,075	21
641	1352	−0.372606	39.4733964	682,947	23,706,756	20
108	1075	−0.3730155	39.4706526	394,955	21,838,165	18

Source: compiled by the authors.

.

In this new situation, the centroid of the risk cluster is policyholder 667. The risk cluster consists of a total of 34 policyholders. As we can see in Table 3, the highest risk for the insurance company is quantified at 45,090,147 euros. In Figure 5, the new risk cluster (the red circle) and the risk cluster under Scenario 1 (the gray circle) have been identified.

5. Conclusions

This paper presents a methodological proposal to calibrate the catastrophic risk of fire caused by human activity to obtain the highest risk cluster for an insurance company. Although the Solvency II regulations indicate in detail and regularly what risks this sub-module must include, it does not offer any market proxy or frame of reference that serves as a guide for obtaining the necessary input [2] (pp. 85–86). In addition, there is no reference as to how to approach this in the scientific or professional field. Beirut´s recent events should serve as a reminder of the importance of a correct assessment of this risk sub-module.

A simplified version of the R function written to implement the procedure can be found in Appendix C. To illustrate this procedure for obtaining the highest risk cluster, a dataset of 1000 policyholders is used. The calculation proposal presented here constitutes a reference method for all European insurance companies covered by the Solvency II regulatory framework, among which the principle of proportionality must prevail at all times.

According to Solvency II, insurance companies must calculate the capital requirement for fire risk to determine the set of buildings with the largest sum insured partly or fully located within a radius of 200 m.

In the spirit of Solvency II, policyholder 2266 has been identified as the centroid of the highest risk cluster, with the highest sum insured at 41,431,645 euros or 49,925,568 euros, depending on the distance used. In this sense, it is essential to highlight that precision of the highest risk clusters’ estimation depends fundamentally on the correct geolocation of the insured risks and the methodological approach used to calculate the distances. In this paper, three different distances were used: Harversine, Vincenty, and Euclidean distances. However, we need to take into account that the Haversine distance calculates the great circle distance on a sphere, while the Vincenty distance calculates the shortest geodesic distance on a slightly ellipsoidal surface. Consequently, the Haversine distance can be in error up to 0.5%. Since the results obtained in our study with the different distances are quite similar, they are preferable because the Vincenty distance is time consuming.

As a suggestion for future research, one of the lines of improvement in the calibration of this sub-risk should be directed towards making changes in the determination of risk exposure to better adjust the occurrence of the extreme event. The introduction of a corrective factor to the sum insured may be pertinent given that in contrast to calculating hypothetical damages produced by the loss, the actual loss would be more significant at the center of a high risk than at the margins of the 200 m considered.

Finally, in the model proposed in this paper, the origin of the catastrophe has been considered to be located within a radius of 200 m of a policyholder, which is the criterion most commonly accepted by professionals in the sector. However, it is possible that the loss may occur at any other point but affect the company’s policyholders. We are currently working on the issue, but it must be borne in mind that the solution to this problem involves exceptionally high computational requirements, even more so given the large volume of most portfolios of European insurers.