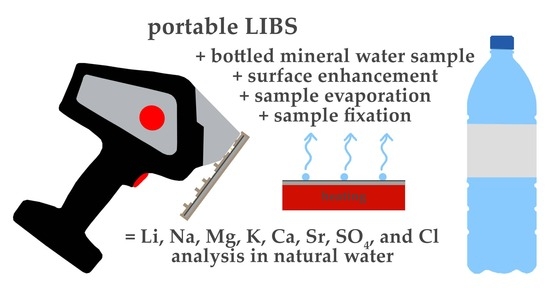
Utilising Portable Laser-Induced Breakdown Spectroscopy for Quantitative Inorganic Water Testing

Abstract

At present, the majority of water testing is carried out in the laboratory, and portable field methods for the quantification of elements in natural waters remain to be established. In contrast, portable instruments like portable X-ray fluorescence (pXRF) analysis and portable laser-induced breakdown spectroscopy (pLIBS) have become routine analytical methods for the quantification of elements in solids. This study aims to show that pLIBS can also be used for chemical compositional measurements of natural waters. Bottled mineral waters were selected as sample materials. A surface-enhanced liquid-to-solid conversion technique was used to improve the detection limits and circumvent the physical limitations in liquid analysis. The results show that low to medium mineralised waters can be analysed quantitatively for their ions using the documented method. For more highly concentrated samples, typically above an electrical conductivity (EC) of 1000 µS/cm, further adjustment is required in the form of self-absorption correction. However, water with a conductivity up to this limit can be analysed for the main cations (Li⁺, Na⁺, Mg²⁺, K⁺, Ca²⁺, and Sr²⁺) as well as the main anions (SO₄²⁻ and Cl⁻) using the documented method. This study demonstrates that there is significant potential for developing field-based pLIBS as a tool for quantitative water analysis.

1. Introduction

An understanding of water quality is traditionally obtained using laboratory-based analyses and continuous monitoring techniques [1,2,3]. This is despite the need for fast, reliable, and, if possible, inexpensive in-field measurement methods, particularly in remote regions. Although hand-held instruments like portable X-ray fluorescence (pXRF) and portable laser-induced breakdown spectroscopy (pLIBS) have been established in geochemical analysis of solid samples for many years [4,5,6,7], inorganic water analyses are still performed almost exclusively in the laboratory [2]. Typical equipment used includes ion chromatography (IC), atomic absorption spectroscopy (AAS), and inductively coupled plasma-mass spectroscopy (ICP-MS). These techniques require trained personnel and proper sample transport, storage, and handling prior to analysis; are expensive to maintain; and are time consuming [8]. This often prevents quick action, as it can take more than a week from the time the sample is taken to the actual analysis of samples and data generation. In addition, in less developed countries, analyses are less likely to be carried out due to the cost and expertise required. Therefore, reliable field instruments are needed to quantify as many elements and compounds as possible. In on-site analysis, lower sensitivity and higher detection limits are usually accepted, if immediate results and higher data density are feasible, especially if pre-screening is performed [4,9].

Typical field-ready measuring equipment for inorganic water analysis available on the market includes photometers, test kits, and ion selective electrodes. The main reason why field methods have not yet been widely adopted for measuring the inorganic chemistry of waters is presumably due to the fact that reliable methods for simultaneous determination of a range of elements have not been developed to date.

Laser-induced breakdown spectroscopy (LIBS) is an atomic emission spectroscopy technique capable of simultaneously determining the complete elemental chemistry of a sample. A focused, pulsed laser beam is directed at a sample to form a plasma containing the elements of the small sample volume that is being ablated. By spectral analysis of the emitted light, it is possible to obtain qualitative and quantitative data on the elements present, provided a suitable calibration is used [4,6]. Although LIBS currently plays rather a niche role in water analysis, several studies have shown that laboratory-based LIBS systems can be used to simultaneously quantify almost any element in water with very low detection limits [10,11,12,13,14,15,16,17,18,19,20,21,22,23]. For example, Na has been quantitatively analysed in aqueous solutions with a detection limit of 0.57 μg/L [20]. Mg, Ca, Sr, and Ba have been detected down to 0.3, 0.6, 1.0, and 0.7 ppm, respectively [16], and Mg, Cr, Mn, and Re have been detected down to 0.1, 0.4, 0.7, and 8 mg/L, respectively [11].

However, many of these laboratory applications described use complicated experimental setups, such as measurement in a liquid jet [11,20] or liquid to aerosol [16]. This is because direct bulk liquid analysis by LIBS is prone to low sensitivity and accuracy due to energy losses as a result of liquid evaporation, plasma cooling, and intense splashing [24]. A simpler sample preparation method, which is also feasible in the field and adaptable to a portable laser-induced breakdown spectroscopy (pLIBS) instrument, is liquid-to-solid conversion (LSC). At the same time, this method offers the advantage that the detection limits are lowered by pre-concentration. Therefore, in a previous work, a surface-enhanced (SE) liquid-to-solid conversion (LSC) method was adapted to a pLIBS for quantitative analysis of Li, Na, and K in standard solutions containing nearly no other cations [25]. Instead of directly shooting the liquid with the laser, the evaporation residue (EvR) was analysed on a commercially available aluminium foil, which was SE with a thin layer of graphite pencil powder. Low detection limits could be achieved by LSC while avoiding negative physical effects such as splashing and cooling of the plasma that occur when analysing liquid samples. Moreover, by preparing the aluminium foil with pencil powder, the surface became more hydrophobic, and therefore, the EvR were distributed more homogenously, leading to better reproducibility. A self-designed template that fits on the nose of the SciAps Z-300 guaranteed fixation during the analysis of 100 positions in a fixed grid on and around the EvR. Results of the study showed that a portable LIBS analyser is well suited for the quantitative analysis of light alkali elements in standard solutions up to 160 mg/L [25]. To our knowledge, that was the first time that a handheld LIBS instrument had been used to quantify dissolved elements in aqueous solutions using an LSC technique. The portability of the method opens up new possibilities for on-site screening and quantitative analysis of inorganic water chemistry.

However, to date, the method has only been applied to single-element standard solutions. In order to identify possible matrix effects and to further adapt the method for field use, bottled mineral waters from different manufacturers and with as diverse a chemistry as possible were chosen as examples in this study (see

Table 1. List of bottled mineral waters analysed by this study.

Abbr.	Name/Brand	Spring	Location	State	Country	Bottle	TDS (mg/L)	EC (µS/cm)
Adhz	Adelholzener	Adelholzener Alpen Quell	Bergen	BY	De	PET	511	598
AqMi	Aqua Mia	Geotaler	Löhne	NW	De	PET	1284	1575
BeWa	Bergische Waldquelle	Bergische Waldquelle	Haan	NW	De	PET	159	257
Blk	Blank sample	-	laboratory	-	-	HDPE		1.3
Extl	Extaler-Mineralquell	Extaler-Mineralquell	Rinteln-Exten	NI	De	TP	1603	1708
Fach	Staatl. Fachingen	Staatl. Fachingen	Fachingen	RP	De	glass	4306	2726
Gest	Gerolsteiner Naturell	Naturell	Gerolstein	RP	De	PET	807	878
Laur	Lauretana	Lauretana	Graglia	21	It	PET	17	20.5
Löng	K-Classic	Quelle Löningen	Löningen	NI	De	PET	162	275
Mar	Marius-Quelle	Marius-Quelle	Sachsenheim	BW	De	PET	2435	2650
Nat	Naturalis still	Urstromquelle	Wolfhagen	HE	De	PET	126	212
Odwq	Odenwald-Quelle	Odenwald Quelle	Heppenheim	HE	De	PET	760	727
Qubr	Quellbrunn Werretaler	Werretaler	Löhne	NW	De	PET	729	971
Rosb	Rosbacher Naturell	Rosbacher Naturell	Rosbach v.d. Höhe	HE	De	PET	1235	1363
Saw	Sawell	Genussquelle 3	Emsdetten	NW	De	PET	377	589
Vit	Vittel	Vittel Bonne Source	Vittel	88	Fr	PET	490	444

BY = Bavaria, NW = North Rhine-Westphalia, NI = Lower Saxony, RP = Rhineland-Palatinate, BW = Baden Württemberg, HE = Hesse, 21 = Piemont, 88 = Département des Vosges, De = Germany, It = Italy, Fr = France, PET = polyethylene terephthalate, HDPE = high-density polyethylene, TP = Tetra Pak, TDS = total dissolved solids (as indicated), EC = electrical conductivity (as measured).

and Figure 1). When using bottled mineral waters from grocery stores, it is possible to choose from a wide range of different mineralised waters, as the manufacturers in the European Union are obliged to print analysis results on their bottles. These may often not be particularly up to date, but they provide a rough guide on the likely chemical composition of bottled waters. There has also been a lot of research into the testing of bottled mineral water for mineralisation [26,27,28,29]. As can be seen in Figure 1, the choice of bottled mineral water allowed very different types of water to be selected. This is important in order to have a diverse test series to study possible matrix effects.

In this study, the analytical approach of the former study [25] was extended to include elements and compounds (Ca²⁺, Mg²⁺, Sr²⁺, Cl⁻, SO₄²⁻, and NO₃⁻) to cover the main cations and anions in natural waters and documented on bottled mineral water. The results of this study therefore contribute to the ongoing development of hydrochemical field testing tools.

2. Materials and Methods

2.1. Sample Preparation

Water samples were taken from commercially available bottled mineral waters purchased from supermarkets. Fifteen different brands were chosen, and waters with the most diverse chemistry according to their information labels were selected to obtain a diverse test series (Table 1 and Figure 1). Only non-carbonated bottled water was selected to compensate for precipitation by degassing. With two exceptions (Fach., glass, and Extl., Tetra Pak), all mineral waters were bottled in PET. Two 50 mL samples of each mineral water were prepared by filling centrifuge tubes. One was acidified with HNO₃ to prevent precipitation (cation sample). The anion sample was not prepared further. An additional blank sample was prepared from distilled deionised water (18 MΩ) in the same way as the mineral waters. A portion of each anion sample was used for the analysis of physico-chemical parameters (temperature (T), electrical conductivity (EC), pH, and HCO₃⁻) and pLIBS analysis before all samples were sealed with Parafilm^® and sent directly to the laboratory for subsequent ion exchange chromatography (IC) and inductively coupled plasma–mass spectrometry (ICP-MS) analysis (Technical University of Darmstadt, Darmstadt, Germany).

For subsequent measurements, aqueous single-element AAS standard solutions on a 2% nitric acid basis with a concentration of 1000 mg/L were used for the calibration of the cations (ROTI^®Star, Carl Roth, Karlsruhe, Germany). From each of the standard solutions, 16 different concentrations ranging from 0.1 to 1000 mg/L were prepared by diluting with 2% nitric acid. The latter was made by diluting 65% nitric acid (ROTIPURAN^® ≥ 65%, Carl Roth, Karlsruhe, Germany) with distilled deionised water (18 MΩ). Li⁺, Na⁺, and K⁺ were prepared as single-element standard dilution series. Mg²⁺ and Ca²⁺ were mixed with each other as paired standard dilution series. Concentrations above 500 mg/L were prepared as single-element standards. The same procedure was used for Zn²⁺ and Sr²⁺. In addition, a water-based multi-element anion IC standard solution containing Cl⁻, SO₄²⁻, and NO₃⁻ was used to calibrate the main anions by dilution with distilled deionised water at concentrations ranging from 0.5 to 1000 mg/L.

Furthermore, mixed solutions were prepared by using the single-element standard solutions in equal amounts and diluting with 2% nitric acid. Six mixed solutions containing Li, Na, and K (ranging from 2 to 250 mg/L) and six containing Li⁺, Na⁺, K⁺, Mg²⁺, Sr²⁺, and Ca²⁺ (ranging from 1 to 125 mg/L) were prepared. Cl⁻, SO₄²⁻, and NO₃⁻ were not included in the mixed standards, as the cationic single element standards already contained nitrate in different quantities.

2.2. Instrumentation

As in the previous study [25], the commercially available handheld LIBS analyser SciAps Z-300 (SciAps, Woburn, MA, USA) was used. It contains a class 3B Nd:YAG laser that produces laser light with a wavelength of 1064 nm and an energy of 5–6 mJ/pulse with a duration of 1 ns and an adjustable firing rate of between 1 and 50 Hz [30]. Three spectrometers consisting of time-gated charge-coupled diodes (CCD) detect the emitted light in the spectral range of 190–950 nm by three spectrometers [30].

The acquisition settings of the pLIBS analyses have been detailed by a previous study [25]. Due to the small size of the EvR after LSC and the possibility of laying a raster over an area with the SciAps Z-300, it was possible to analyse the whole EvR and a small area around it. One hundred locations were fired at four times each in order to obtain data. For each location, the four individual analyses were averaged into a spectrum, resulting in 100 spectra per sample. Since fresh samples were applied to the SE aluminium foil, no cleaning shots were needed, and this setting was set to 0. The use of gating can improve the signal-to-noise ratio because the continuum radiation, which contains no useful information and occurs mainly at the beginning of a measurement, has a lower proportion with a slightly delayed measurement [23]. In the previous study, the gate delay for Li, Na, and K was optimised [25]. In order to obtain comparable data, the gate delay was not further adjusted in this work. An internal integration delay (IID) of 84 was used, corresponding to a delay time (t_d) of approximately 2 µs. In order to achieve signal enhancement [30,31], an Ar atmosphere was used for the measurements. The coordinates were set to start at 100, 100, 70 and end at 350, 350. Finally, the test rate was set to 50 Hz. A custom stencil designed for the SciAps Z-300 described in [25] was used to facilitate and speed up handling by fixing the substrate and the device itself.

2.3. Liquid Analysis

First, the pH and EC of each bottled mineral water were determined. For this purpose, the bottled waters were poured into centrifuge tubes large enough to fit the probes of the pH and conductivity electrode. This method has already been described by [32] and helps to reduce the required sample volume. In this study, a slightly larger sample volume of about 20–25 mL was used. Conductivity and temperature were measured first (CA 10141 with conductivity probe XCP4ST1, Chauvin Arnoux, Asnières-Sur-Seine, France), making sure that the probe was thoroughly cleaned with distilled water and then dried before measurement. Afterwards, the pH value was analysed with a likewise cleaned probe (HI 991002 with pH/ORP probe HI1297, Hanna Instruments, Vöhringen, Germany). Hydrogen carbonate was measured with a field-ready photometer (HI775 Checker HC, Hanna Instruments, Vöhringen, Germany) using a sample of maximum 15 mL.

For the comparative measurements in the laboratory, one cation and one anion sample were prepared, the former being acidified with 10 droplets of 10% nitric acid (diluted ROTIPURAN^® ≥ 65%, Carl Roth, Karlsruhe, Germany) to prevent precipitation. The samples were analysed for the main cations and anions with IC at the Institute of Applied Geosciences of Technical University of Darmstadt (Metrohm 882 Compact IC plus, Metrohm, Herisau, Switzerland).

Sr and Zn were analysed using ICP-MS (Analytik Jena Plasma Quant MS Elite^®, Jena, Germany). Instrumental conditions were optimised using a 1 µg/L tuning solution (diluted 10 mg/L Analytik Jena Tuning solution, Jena, Germany), leading to high sensitivities of the containing elements Be, In, Pb, and Th in the tuning solution with simultaneous low oxide and a doubly charged ion ratio. Helium was used as a collision gas in the integrated collision–reaction cell (iCRC) for the minimisation of potential interferences. A 10 µg/L Y solution (diluted ROTI^®Star 1000 mg/l Y, Carl Roth, Karlsruhe, Germany) was added online via a peristaltic pump to all samples and standards in order to compensate for drifts of the ICP-MS system. Standard deviations of laboratory analyses are provided in

Table A2. Relative standard deviations (RSDs) and detection limits (LoDs) of IC and ICP-MS* analysis.

Abbr.	Li	Na	Mg	K	Ca	Sr*	SO4	Cl	Unit
RSD	0.611	0.476	0.449	0.666	0.355		0.149	0.072	%
LoD	0.028	0.019	0.059	0.053	0.098	0.0000214	0.218	0.075	mg/L

.

The ion balances were calculated from the equivalent concentrations of the cations and anions according to [33]. High ion balance deviations are an indication that certain ions have not been recorded or have been recorded incorrectly. The algebraic sign is an indicator of whether the error could be on the anion or cation side. Another plausibility check is the calculation of the EC of a water sample from the main cations and anions [34]. This method was used to evaluate whether there was any inconsistency between the measured and calculated conductivity, indicating that certain cations or anions had not been detected or had been incorrectly detected.

The underlying method for the analysis of cations and anions in water with pLIBS has been presented in detail by [25] for the three alkali elements Li, Na, and K. Here, the SE aluminium foil, prepared with a thin layer of pencil powder, was placed between the base and the stencil and the sample solutions were applied through the recesses using a micropipette (cf. Figure 2). A total of 0.75 µL of the sample solutions was applied to the aluminium foil in the same way each time with the help of an auxiliary line. In this way, 15 droplets can be placed on one sample foil. After application, the aluminium foil was removed and heated on the heating table to achieve LSC until only the EvR remained. The aluminium foil was then placed back between the base and the stencil and the EvR was analysed with the pLIBS. Standard deviations and relative standard deviations of replicate pLIBS analyses are provided in

Table A3. Standard deviations (SDs) calculated from five pLIBS (Adhz: 15) measurements per water sample and median values of the relative standard deviations (RSDs) for the elements investigated. Readings below the detection limit were not included in the calculation of the RSD. For this reason, no RSD could be calculated for Li.

SD	Li	Na	Mg	K	Ca	Sr	SO4	Cl	Unit
Adhz	0.06	4.21	4.86	0.73	3.08	0.23	13.51	4.56	mg/L
BeWa	0.06	1.89	0.51	0.54	2.62	0.00	7.00	2.14
Blk	0.03	0.13	0.05	0.29	0.13	0.01	14.01	3.31
Gest	0.06	4.23	4.94	0.97	5.28	0.08	7.00	1.65
Laur	0.04	0.29	0.10	0.34	0.18	0.01	8.58	3.02
Löng	0.05	3.21	0.21	0.20	3.23	0.01	8.58	3.44
Nat	0.05	2.44	0.96	0.88	4.33	0.01	13.10	2.70
Odwq	0.10	1.60	1.78	1.08	3.03	0.09	7.00	1.65
Rosb	0.07	2.37	3.05	1.08	2.26	0.01	8.58	2.14
Saw	0.15	9.52	0.74	0.71	4.24	0.03	11.07	2.53
Vit	0.16	2.34	3.37	1.88	7.22	0.16	7.00	2.14
Median RSD	-	25	17	29	11	22	39	26	%

. By fixing the nose of the device, it is possible to quickly switch between the individual samples without additional focusing. In addition, the measuring device does not slip during the measurement of the 100 spots per EvR.

2.4. Calibration Settings

With the calibrations in this work, it should later be possible to examine as wide a range of differently mineralised waters as possible. It can thus be assumed that the matrices in the EvR will also vary strongly. However, even small changes in the matrix, e.g., due to different concentrations of the analytes, alter the physical and chemical properties in the plasma to such an extent that the emitted signal is no longer proportional to the concentration. This leads to so-called matrix effects [35]. To compensate for matrix effects [35], multivariate calibration was performed for all elements of interest (EoI) using multiple linear regression (MLR). Using the intensities of Al in the denominator to normalise the numerator (analyte) adds an internal standard [35,36], as Al foil was used as a substrate. Intensity ratios (IR) were calculated by using the intensities of the EoI in the numerator (analyte) and Al intensities in the denominator. The intensities chosen for both the EoIs and Al were selected to avoid possible overlap of nearby peaks of other EoIs due to peak broadening and to maintain an equal sequence of intensities as the concentration of the analytes increases and constant intensity at the intensities of the standard. For this reason, small changes were also made to the lines used for Li, Na, and K compared to [25]. The spectral lines used for calibration in this study are listed in

Table 2. Statistical assessment of the calibrations for single-element standards (Li, Na, K) and paired-element standards (Mg/Ca, Zn/Sr, NO₃/SO₄/Cl).

z	EoI	State	λ	LoD	Range	y	R2	RMSE	S
			nm	mg/L	mg/L			mg/L	mg/L
3	Li	I	497.1	0.006	0.1–2.5	28.133x − 0.3725	0.918	0.17	0.18
		I	610.4		2.5–100	37.973x − 2.3069	0.995	6.65	6.71
		I	670.8		100–1000	11.632x2.1134	0.954	202.18	204.19
		I	812.9
11	Na	II	330.2	0.014	0.1–2.5	45.219x + 0.0149	0.971	2.00	2.03
		I	589.0		2.5–100	184.47x − 11.45	0.960	3.54	4.01
		I	589.6		100–1000	8152.3x8.359	0.538	1131.01	1141.34
		I	818.3
		I	819.5
12	Mg	II	279.6	0.008	0.1–10	78.378x − 0.0589	0.979	0.00	0.00
		II	279.8		10–100	173.46x − 14.439	0.973	6.83	6.93
		II	280.3		100–1000	-	-	-	-
		I	285.2
		I	293.6
		I	382.9
		I	383.2
		I	383.8
		I	516.7
		I	517.3
		I	518.4
19	K	I	691.2	0.006	0.1–10	343.08 + 9.4034	0.987	0.49	0.49
		I	693.9		10–160	292.55x + 9.7589	0.973	10.70	10.82
		I	766.5		160–1000	62.902e1.6945x	0.913	266.10	269.77
		I	769.8
20	Ca	II	315.9	0.021	0.1–2.5	23.014x − 0.0512	0.990	0.03	0.03
		II	317.9		2.5–100	103.34x − 12.964	0.893	3.79	3.82
		II	318.1		100–1000	−527.31x2 + 2456.7x − 1766.7	0.889	155.42	157.59
		II	370.6
		II	393.3
		II	396.8
		I	422.6
		I	430.2
		I	430.8
		I	443.5
		I	445.5
		I	526.5
		I	527.0
		I	558.9
30	Zn	II	202.6	0.0005	0.1–2.5	621.9x − 0.1649	0.988	0.07	0.07
		I	213.9		2.5–50	544.01 − 0.4883	0.998	1.38	1.40
		I	334.5		50–1000	2449.2x2 + 1115.7x − 94.322	0.989	102.14	103.02
		I	468.0
		I	481.1
		I	636.2
38	Sr	II	215.3	0.0008	0.1–5	38.764x + 0.0607	0.999	0.14	0.14
		II	216.6		5–75	136.68x2 − 0.3885x + 3.2393	0.998	7.64	7.74
		II	338.1		75–1000	6.1616e3.7x	0.851	4708.79	4754.73
		II	407.7
		II	416.2
		II	421.6
		II	430.6
		I	460.7
		I	496.2
		I	525.7
		I	548.1
7	N	II	567.6	0.0017	0.5–160	2014.3x	0.853	105.13	105.97
		II	568.6		160–1000	100.07e7.0029x	0.872	195.30	197.96
16	S	I	921.2	0.0002	0.5–160	175098x + 106.97	0.647	93.42	94.12
		I	922.8		160–1000	109.42e2043.1x	0.829	621.23	629.69
		I	923.7
17	Cl	I	833.3	0.0004	0.5–160	33588x	0.976	97.18	98.04
		I	837.6		160–1000	18.869e561.95x	0.912	1113.22	1126.09
		I	857.5
		I	858.6
		I	894.8
13	Al *	I	236.7
		I	237.3
		I	308.2
		I	394.4
		I	396.1

z = atomic number, EoI = element of interest (EoI), λ = wavelength of the lines used for calibration (* Al used as internal standard), LoD = limit of detection: calculated according to the 3σ-IUPAC criterion (LoD = 3* σB/k) [37], y = formula used for calibration, R² = coefficient of determination, RMSE = root mean square error, S = residual standard deviation, σB = standard deviation of the background signal at the lowest solution concentration, k = slope of the calibration line.

. However, the integration was performed in the same way in SciAps’ Profile Builder, applying the zeroth order derivative and Savitzky–Golay smoothing with 7 and 9 as input values for the analytes and Al, respectively, to filter out noise [25].

For more extensive possibilities in calibration, the IRs were calculated with these settings, exported as a .csv file, and used in a spreadsheet for calibration. Subsequently, outliers were eliminated by 1.5 inter-quartile range (IQR) method. For most concentrations, 15 IR values were used for calibration, of which at least 12 remained after outlier elimination. Some higher concentrations were tested with up to 27 IR values. The mean of the respective IR values per element for blanks was then subtracted from all IR values. Due to effects such as self-absorption at higher analyte concentrations [35], the slope of a single calibration curve over the entire concentration range (0.1–1000 mg/L) changes strongly. Ref. [21] encountered the same problem when analysing K, Na, Ca, and Mg in liquid solutions dried on filter paper. They had to use two calibration lines over the concentration range of 10–1000 mg/L [21]. Therefore, in this work, three concentration ranges were defined for all cationic species, which were chosen differently due to the different slopes for the individual elements. Only two concentration ranges were defined for the anionic species. Wherever possible, linear calibration lines were used. For higher concentration ranges, exponential or quadratic calibrations were often required. The different concentration ranges are listed in Table 2. According to the 3σ-IUPAC criterion [37], LoDs for the EoI were calculated and are also listed in Table 2. Within the concentration ranges, other statistical parameters are given, such as the coefficient of determination (R²) of the calibration lines, the root mean square error (RMSE) of the regression, and the residual standard deviation based on the regression (S).

3. Results

In Table 2, the statistical evaluation of the calibrations for single-element standards (Li, Na, K) and paired-element standards (Mg/Ca, Zn/Sr, NO₃/SO₄/Cl) is shown. The calculated LoDs were quite low (<0.03 mg/L) and therefore notably lower than the lowest concentration used for calibration (0.1 mg/L). In general, high coefficients of determination (R²) were obtained for the low and medium concentration ranges. The third concentration range generally suffered from lower R² and higher RMSE and S (e.g., Na, Sr). The analysis of anionic species was generally less sensitive than that of cationic species, as indicated by the high to very high RMSE and S. It was not possible to establish a calibration line for Mg above 100 mg/L, as the IR did not increase with further increases in concentration. The calibration curves for Sr are shown in Figure 3. In order not to go beyond the scope of this paper, the other calibration curves are not shown here.

By applying the calibration curves provided in Table 2, subtracting the respective IR blank values (see

Table A1. Threshold values (THV) for selecting the correct formula according to the concentration range and the mean values of the blank IR (mean b), which were subtracted from the calculated IR values. THV I = transition of the first to the second concentration range. THV II = transition of the second to the third concentration range. Unitless IR values are given.

	Li	Na	Mg	K	Ca	Sr	SO4	Cl
THV I	0.100	0.070	0.130	0.020	0.175	0.140	0.0002	0.0028
THV II	3.000	0.600	0.700	0.550	1.000	0.850
mean b	0.015	0.0141	0.0222	0.022	0.0093	0.0019	0.0003	0.0001

) and using the respective threshold values from Table A1 to select the correct concentration range, the results of the analysis of the bottled mineral waters were obtained and are given in

Table 3. Results of the analysis with the pLIBS compared to laboratory analysis (lab), excluding SO₄ and Zn. pLIBS values are presented as the mean of five measurements (Adhz: 15). All bottled mineral waters with a conductivity above 1000 µS/cm were omitted. Standard deviations are given in Table A2 and Table A3. Laboratory analyses were performed using ion exchange chromatography (IC) except for Sr (inductively coupled plasma–mass spectrometry (ICP-MS)). The absolute deviation (dev) and the relative deviation (r-dev) of the pLIBS from the laboratory value are given for each value. The ionic balance (IB) was calculated using additional hydrogen carbonate values measured with a field photometer. Electrical conductivity was calculated according to [34] for both laboratory and LIBS analysis.

Abbr.		Li	Na	Mg	K	Ca	Sr	SO4	Cl	Unit	IB	EC
											eq-%	µS/cm
Adhz	lab	<LoD	11.95	30.63	1.26	18.40	1.891	28.46	18.95	mg/L	−41.3	496	lab
	pLIBS	<LoD	16.11	22.69	0.32	18.74	1.460	<LoD	16.71	mg/L	−44.9	434	pLIBS
	dev	0.022	4.16	7.94	0.95	0.34	0.431	28.46	2.24	mg/L		598	meas
	r-dev	78.6	34.8	25.9	74.8	1.9	22.8	100	11.8	%	−3.7	−164	dev
BeWa	lab	<LoD	6.19	6.96	0.97	30.16	0.103	21.81	15.46	mg/L	−0.7	252	lab
	pLIBS	<LoD	9.41	7.06	1.86	40.15	<LoD	17.98	11.08	mg/L	30.2	277	pLIBS
	dev	0.022	3.21	0.10	0.88	9.99	0.1022	3.83	4.37	mg/L		257	meas
	r-dev	78.6	51.9	1.4	91.1	33.1	99.2	17.5	28.3	%	30.9	20	dev
Blk	lab	<LoD	<LoD	<LoD	<LoD	0.24	0.004	1.68	2.01	mg/L	−171.2	17	lab
	pLIBS	<LoD	<LoD	<LoD	0.01	<LoD	<LoD	<LoD	0.28	mg/L	−193.6	9	pLIBS
	dev	0.022	0.005	0.051	0.047	0.077	0.003	1.68	1.73	mg/L		1	meas
	r-dev	78.6	26.3	86.4	88.7	78.6	79.4	100	86.2	%	−22.4	8	dev
Gest	lab	<LoD	11.86	39.42	4.45	31.57	0.529	24.23	20.61	mg/L	−45.8	684	lab
	pLIBS	<LoD	13.71	22.08	4.96	33.25	0.363	10.98	6.36	mg/L	−61.8	573	pLIBS
	dev	0.022	1.85	17.34	0.52	1.69	0.166	13.25	14.25	mg/L		878	meas
	r-dev	78.6	15.6	44.0	11.6	5.3	31.4	54.7	69.2	%	−15.9	−305	dev
Laur	lab	<LoD	0.97	0.34	0.36	1.38	0.010	3.21	2.13	mg/L	−73.2	26	lab
	pLIBS	<LoD	0.46	0.04	0.01	1.74	< LoD	42.50	0.95	mg/L	−163.0	81	pLIBS
	dev	0.022	0.51	0.29	0.35	0.36	0.009	39.29	1.18	mg/L		21	meas
	r-dev	78.6	52.1	86.9	98.3	26.2	91.8	1225	55.3	%	−89.9	60	dev
Löng	lab	<LoD	15.05	3.23	1.70	30.33	0.066	40.08	28.79	mg/L	4.8	281	lab
	pLIBS	<LoD	21.31	3.23	4.17	30.05	0.001	24.99	22.56	mg/L	29.1	278	pLIBS
	dev	0.022	6.25	0.00	2.47	0.28	0.065	15.09	6.22	mg/L		275	meas
	r-dev	78.6	41.5	0.0	145	0.9	98.8	37.6	21.6	%	24.3	3	dev
Nat	lab	<LoD	6.28	7.01	3.09	22.48	0.057	12.02	9.29	mg/L	46.8	177	lab
	pLIBS	<LoD	5.21	6.05	2.60	37.28	0.001	0.00	6.36	mg/L	98.8	182	pLIBS
	dev	0.022	1.07	0.96	0.49	14.80	0.056	12.02	2.94	mg/L		212	meas
	r-dev	78.6	17.0	13.7	15.8	65.9	98.6	100	31.6	%	52.1	−30	dev
Odwq	lab	0.036	13.04	23.87	5.83	41.52	0.834	17.56	24.54	mg/L	−42.7	592	lab
	pLIBS	<LoD	22.15	15.25	10.54	36.16	0.694	35.49	19.86	mg/L	−57.1	602	pLIBS
	dev	0.030	9.11	8.62	4.71	5.37	0.140	17.94	4.68	mg/L		727	meas
	r-dev	83.3	69.9	36.1	80.7	12.9	16.8	102	19.1	%	−14.4	−125	dev
Rosb	lab	<LoD	59.91	65.13	3.09	30.59	0.284	18.15	91.57	mg/L	−9.2	1016	lab
	pLIBS	0.057	57.49	42.53	7.67	37.75	0.001	0.0002	44.85	mg/L	−16.4	876	pLIBS
	dev	0.029	2.42	22.60	4.58	7.17	0.284	18.15	46.72	mg/L		1363	meas
	r-dev	103	4.0	34.7	148	23.4	100	100	51.0	%	−7.3	−487	dev
Saw	lab	<LoD	18.73	3.52	1.17	71.03	0.722	58.00	52.78	mg/L	3.7	524	lab
	pLIBS	<LoD	41.18	4.29	0.62	65.17	0.296	0.0002	32.02	mg/L	60.5	439	pLIBS
	dev	0.022	22.45	0.78	0.55	5.86	0.427	58.00	20.76	mg/L		589	meas
	r-dev	78.6	120	22.1	47.1	8.2	59.0	100	39.3	%	56.8	−150	dev
Vit	lab	0.055	6.02	19.45	5.07	54.26	0.877	113.17	6.87	mg/L	5.0	511	lab
	pLIBS	<LoD	5.93	11.94	7.16	43.63	0.764	70.51	4.33	mg/L	1.5	390	pLIBS
	dev	0.049	0.09	7.51	2.09	10.63	0.113	42.65	2.54	mg/L		444	meas
	r-dev	89.1	1.5	38.6	41.4	19.6	12.9	37.7	37.0	%	−3.6	−54	dev
Median r-dev		78.6	34.8	34.7	80.7	19.6	79.4	100.0	37.0	%

Adhz = Adelholzner, BeWa = Bergische Waldquelle, Blk = blank sample, Gest = Gerolsteiner, Laur = Lauretana, Löng = Löningen, Nat = Naturalis, Odwq = Odenwaldquelle, Rosb = Rosbacher, Saw = Sawell, Vit = Vittel.

. The values were compared with the laboratory analyses (IC and ICP-MS). The absolute and relative deviations are provided. In addition, ion balances of all waters are presented and were compared between the laboratory and the pLIBS analysis. The electrical conductivities calculated from the laboratory and pLIBS analyses are shown and the latter were compared with values measured before the analysis. As highly mineralised bottled mineral waters, typically above 1000 µS/cm, showed very low accuracy, these were excluded from evaluation in order to increase clarity. In addition, Zn and NO₃ were excluded, as they showed low analytical performance (low accuracy—in particular, inconsistent overestimation).

Figure 4, Figure 5 and Figure 6 show correlations between pLIBS predicted concentrations and laboratory concentrations for all EoIs, excluding bottled mineral waters with a conductivity greater than 1000 µS/cm. Of these, Figure 4 shows only the singly charged cations (alkali metals) and Figure 5 the doubly charged cations (alkaline earth elements). The correlations for the anionic species, excluding NO₃, are illustrated in Figure 6.

Figure 7 shows combined Stiff diagrams for all selected bottled mineral waters. Stiff plots simplify the comparison of waters [38] and are usually applied to compare different waters—for example, to illustrate spatial or temporal differences in water chemistry. Here, combined Stiff diagrams were used to compare the same water in different analyses (pLIBS and laboratory). For each water sample, a Stiff diagram is shown for the laboratory and for the pLIBS analysis results. Perfectly matching analyses should produce exactly the same polygon for both analyses. Since an additional photometer was used for the HCO₃ concentrations, the results for laboratory and LIBS analysis are identical for HCO₃.

Figure 8 and Figure 9 show the results of applying the calibrations used for single-element or paired-element standard solutions (Table 2) to mixed standard solutions. The first of the two figures shows the results of the mixed test series containing all three singly charged cations simultaneously (cf. Figure 8). K concentrations appear to have been slightly underestimated for prepared concentrations below 10 mg/L and overestimated for prepared concentrations between 40 mg/L and 75 mg/L. For higher concentrations, the prepared concentrations were clearly underestimated. Li concentrations were slightly overestimated for concentrations up to 30 mg/L, fit relatively well for concentrations up to 80 mg/L, and were underestimated for even higher concentrations. Na concentrations up to 20 mg/L seem to have fit well, but at higher prepared concentrations the predicted concentrations also seem to have been underestimated.

Figure 9 shows the results of the test series with mixed standards containing all six cations simultaneously. Compared to the mixed standards with less different cations, all three alkali elements seem to have behaved differently. The overestimation at low concentrations and underestimation at high concentrations was even more pronounced for Li, Na, and K in the second series of tests. Li, in particular, changed and ended up behaving very similarly to Na. It is noticeable that the alkaline earth metals (doubly charged cations) Mg, Ca, and Sr behaved similarly to each other but quite differently to the alkali elements (singly charged cations). They were more clearly underestimated at higher concentrations but not overestimated at low concentrations. For all elements in both test series, there appears to have been a plateau at higher concentrations where even higher concentrations did not produce more signal and therefore a predicted concentration. Attenuation at higher concentrations appears to have been greater for alkaline earth elements (divalent cations) than for alkali elements (monovalent cations). A series of attenuations can be formed from low to high: K < Li < Na < Mg < Sr < Ca.

4. Discussion

All calculated LoDs were quite low (in the ppb range). However, these low detection limits are deceptive. The lowest concentrated standard used was 0.1 mg/L for the cations and 0.5 mg/L for the anions. Nevertheless, the highest LoD calculated was 0.021 mg/L (Ca). It is particularly striking that the detection limits for the anions were particularly low. It has been shown in earlier research that the quantitative analysis of sulphur and chlorine with LIBS is subject to some difficulties and that indirect determination is often necessary to achieve low detection limits [39,40]. This is due to the low excitation in the plasma caused by the high ionisation energy of Cl and S [39]. However, [41] pointed out that the determination of LoDs with the outdated IUPAC formula used in this work is not particularly appropriate for multivariate LIBS analysis [41]. Yet, since this formula is currently the most widely used calculation of the LoD and comparability with [25] should be ensured, a different calculation was not used. Although the absolute detection limits may be somewhat higher in reality, it has been shown that very low concentrations (<0.1 mg/L) can be detected in standard solutions with pLIBS.

It may seem cumbersome to have several calibration curves within one EoI for different concentration ranges, but by using THVs (cf. Table A1) the selection of the correct range and therefore the formula can be completed automatically in a spreadsheet. The advantage of having multiple calibration curves for an EoI at different concentration ranges is that the changing slope of a single curve can be better represented. If self-absorption correction is applied in the future, it may not be necessary to have several concentration ranges but rather only one calibration curve, as the slope will no longer change as much.

The high determination coefficients for Li, Na, and K in [41] could also be achieved for other elements and compounds, especially at low to medium concentrations (cf. Table 2). At higher concentrations (generally > 100 mg/L), the determination coefficients were higher, as expected. For Mg, no calibration line could be established, as the IR did not increase with increasing concentration. This is an indication of strong self-absorption [35].

Zn, and NO₃ were excluded from the evaluation, as they showed low analytical performance. For Zn, on the one hand, the test series was not diverse enough to make statements on the applicability to natural waters and, on the other hand, the measured values were clearly overestimated. NO₃ concentrations showed no clear correlation between pLIBS and IC analysis, with a strong tendency of overestimation. For the pLIBS analysis of NO₃, it cannot be excluded that the results were partly falsified. It is possible that some cation samples were used for the pLIBS measurements instead of the unaltered anion samples. In contrast to the anion samples, these were acidified with HNO₃ (see liquid analyses) to prevent the cations from precipitating during transport to the laboratory for IC and ICP-MS analyses. Since only very small amounts of diluted high-purity nitric acid were used, this should only have had an influence on the nitrate concentrations. However, this would explain why there was no correlation between pLIBS and IC analyses for nitrate.

The median of the relative deviation for all Ca analyses with pLIBS compared to laboratory analyses was fairly good, at 19.6% (cf. Table 3). Figure 5 shows a fairly good correlation between pLIBS and IC data for Ca up to 75 mg/L.

The median of the relative deviation for all Na and Mg analyses with pLIBS compared to laboratory analyses was reasonable, at 34.8% and 34.7%, respectively (cf. Table 3). Figure 4 shows a fairly good correlation between pLIBS and IC data for Na with only one conspicuous outlier with a very high standard deviation (9.52 mg/L). Figure 5 shows a correlation between pLIBS and IC data for Mg, with a tendency for higher concentrations to be underestimated. This trend could be interpreted as a progressive exponential function, which could indicate an increase in self-absorption with increasing concentration.

The median of the relative deviation for all Cl analyses with pLIBS compared to laboratory analyses was still reasonable, at 37.0% (cf. Table 3). Figure 6 shows a fairly good correlation between pLIBS and IC up to 30 mg/L, with a tendency to underestimate higher concentrations, similar to Mg (cf. Figure 5), from which the same conclusions can be drawn.

The median of the relative deviation with pLIBS compared to laboratory analyses was quite high for Li, Sr, and K, at 78.6, 79.4, and 80.7%, respectively (cf. Table 3). However, the test series was not very diverse for Li, with most values close to or below the LoD of the IC analyses (0.027 mg/L). It is therefore hardly surprising that most of the values for the pLIBS Li analysis were also close to or below the LoD of the pLIBS analysis. A large part of the relative deviation for Li thus resulted from the different LoDs between pLIBS and IC analysis. As the test series was not diverse enough for Li concentrations (cf. Figure 4), it is also difficult to say whether there was a good correlation between pLIBS and IC analysis. For Sr, the deviation also mainly came from very low concentrations. Many pLIBS results were below the LoD of 0.0008 mg/L. However, there was a correlation between pLIBS and IC data for concentrations up to 2 mg/L (cf. Figure 5). For K, Figure 4 shows a fairly good correlation between pLIBS and IC data, with a tendency for all concentrations to be slightly overestimated.

The median of the relative deviation for all SO₄ analyses with pLIBS compared to laboratory analyses was quite high, at 100.0% (cf. Table 3). In addition, the correlation between pLIBS and IC data was quite poor (cf. Figure 6).

The IB can help to identify possible analytical discrepancies between cationic and anionic species concentrations. Therefore, a negative IB indicates excessive findings of anionic species concentration or underestimation of cationic species concentration. A positive IB indicates too low an analysed anionic species concentration or too high a cationic species concentration. Seven out of 11 results of IB calculated with pLIBS had a negative IB, which indicates that mostly anions were overestimated and or cations underestimated.

Ideally, the calculated ECs for both analyses (pLIBS and laboratory) should match the measured EC value. A deviation from the measured value is a clear indication of non-analysed or incorrectly analysed ions. If the calculated EC value of the laboratory measurement differs from the measured value, it can be assumed that either ions precipitated, samples were contaminated, or they were measured incorrectly. Looking at the values in Table 3, one water stands out as having had a deviation of more than 30% for the laboratory EC measurements: the blank one. This was mainly due to the low mineralisation of the deionised water, where minimal absolute differences in the analysis result in large percentage deviations. For the pLIBS analysis, 4 of the 11 waters showed a deviation of more than 30% (Blk, Gest, Laur, Löng, Saw). This is an indication that the total of all determined ions for these waters differs from the real solution content.

Furthermore, precipitation of CaCO₃ prior to both pLIBS and IC analysis can be observed by comparing the analysis results with the values indicated on the bottles (Adhz, Gest, Odwq, Rosb, Vit). However, other cations or anions do not appear to have been affected and precipitation occurred prior to analysis, as shown by comparative measurements with newly purchased bottles and re-measurements of the original samples.

The Stiff diagrams perfectly illustrate the differences between pLIBS and laboratory analyses (cf. Figure 7). Based on the agreement between the analyses, the plots can be grouped into two categories: good correlation between laboratory and pLIBS analysis (first row) and moderate correlation (second and third rows). A third category with poor correlation would have been needed for waters with a conductivity greater than 1000 µS/cm or concentrations of several ions >> 6 mmol_eq/L.

For clarity, the uncertainty and the precision of the pLIBS analysis of the bottled waters are reported separately in Table A3 in the Appendix A. Standard deviations (SD) for replicates on one sample in the range of 0.003 to 14.01 mg/L for all selected samples and elements are quite acceptable for a portable instrument, taking into account the diverse chemistry, with up to approximately 120 mg/L solution content per element (cf. Table A3, highly mineralised waters excluded). Looking at the median relative standard deviation (RSD) for the different elements, the values appear quite high. The lowest RSD was 11% (Ca) and the highest 39% (SO₄). However, these values are comparable to the RSDs reported by other authors who analysed aqueous samples by laboratory LIBS. For example, a precision of 2–6% RSD was achieved for aerosol LIBS and a precision of 13–22% for microdrop LIBS [16]. For more similar sample preparation techniques using LSC, 11–17% RSD was achieved for geometric constraint LSC and 25–36% RSD for unconstrained direct LSC [19]. Precision in LIBS analysis is typically low (5–20%) due to shot-to-shot variability and matrix effects [42]. Other effects, such as the slightly different distribution of the EvR, may also occur, resulting in lower precision. It is therefore advisable to perform multiple measurements per sample. At least three or, better, five measurements per sample are recommended for the presented method. Due to the small sample volume required (0.75 µL) and the short measurement time, this can be achieved quickly and easily.

Compared to testing single-element standard solutions [25], it is to be expected that there are more effects affecting the results of an analysis of mixed solutions or natural waters with an even more complex matrix. As LIBS analysis is highly susceptible to the so-called matrix effect [35], small changes in the matrix can cause the emitted signal to be no longer proportional to the concentration. There are several indications of matrix effects in the results of the mineral water analyses. These are particularly evident in the fact that more highly mineralised waters such as Aqua Mia, Extaler, and Marius generally showed very poor analytical results and were omitted from the evaluation. If a suitable self-absorption correction is used in the future, these more highly mineralised waters should also be analysable. In addition, especially for Mg and Cl concentrations above 15 mg/L, there is a systematic underestimation, which can even be seen as a recognisable (progressive) exponential function in the correlation plots (cf. Figure 5 and Figure 6). For the other cations, this effect might also occur if samples with higher concentrations had been analysed. The discarded data for Ca and Sr confirm this assumption. However, the self-absorption effect is difficult to investigate in complex natural waters.

In order to gain a better understanding of this effect, mixed standard solutions were analysed in addition to the bottled mineral waters, and the calibrations developed were used for analysis. A small mixed standard containing Li, Na, and K and a more comprehensive one containing Li, Na, K, Ca, Mg, and Sr were analysed. The results of the two test series show clearly that there were both amplifying and attenuating effects that cancelled out the proportionality (cf. Figure 8 and Figure 9). Nevertheless, a clear correlation is recognisable. This can be described as degressive proportionality, in which the measured concentration increases less and less as the real concentration increases. Typically, with low concentrations attenuating effects can be visible, especially for the light alkali elements Li, Na, and K. This effect was less pronounced in the test series without the doubly charged cations. As with all elements in both test series, a plateau was reached at higher concentrations, where even higher concentrations did not produce significantly more signal and therefore a predicted concentration, the linearity, was cancelled out. This is a clear hint of self-absorption [41]. When using single-element standards, these problems were encountered with concentrations typically above 160 mg/L [25]. This limit seems to have dropped significantly for more complex waters and was more pronounced for the alkaline earth metals than for the alkali elements (cf. Figure 8 and Figure 9).

Typically, self-absorption has several effects on the line shape, so these should be visible in the lines used for calibration. Self-reversal can occur in LIBS analysis when there are spatial gradients in plasma temperature and electron number density. This can lead to a dip at the centre of an emission peak, which can be strong enough to erroneously identify two peaks [43]. In this work, no line showed typical self-reversal effects such as a dip at any maximum. However, this does not mean that there was no self-absorption [44]. Self-absorption was visible in several lines, as the IR did not grow proportionally with increasing concentration (typically above 100 mg/L) and the curve saturated (cf. Figure 8 and Figure 9). This can also be seen in the broadening of the peaks, which resulted in a higher full width half maximum (FWHM) (cf. Figure 10a,b). It can clearly be seen that for both K 769.8 and Li 670.7 the lines not only increased in height with increasing concentration but also became wider. Between 10 and 25 mg/L there was still a large difference in peak height for K 769.8 (cf. Figure 10b). Between 50 and 125 mg/L the difference was already smaller and the height variation at the same concentration was greater. In addition, the lines at 10 mg/L were only a little more than half a nm wide at the base. At 125 mg/L, it was already more than 2 nm. This made integration more difficult. If the integration range is too large, there may be overlap with other peaks. If it is too small, the area under the peaks will be underestimated for higher concentrations. The effect of peak broadening also occurred with all other lines of the other elements and compounds investigated. However, it was particularly pronounced for the higher-intensity peaks.

Ref. [43] did not observe any self-reversal or self-absorption when analysing the liquids directly, even at a concentration of 40,000 mg/L. In contrast to [43], self-absorption played a significant role with increasing concentration when using LSC. However, [43] also found both self-reversal and self-absorption effects when analysing solids, and the main difference in this study is that by analysing the evaporation residue, solids were analysed instead of liquids.

This difference was also highlighted by [43] and attributed to the fact that the atomic densities of analytes in plasma are approximately 1000 times greater for a pure solid than for liquid solutions and are therefore optically thicker.

Ref. [21], who used LSC on filter paper in the concentration range of 0–1000 mg/L, also experienced self-absorption and therefore had to apply two calibration lines per element to fit the data. At lower concentrations, a steeper straight line could be applied than at higher concentrations [21]. This clearly reduced the sensitivity at higher concentrations, as in this work.

The same effect was observed by [17], who also used an SE LSC method. They explained the increased effect of self-absorption by the fact that analytes and standards are concentrated in a very small area after drying [17]. It can therefore be assumed that the effect is even stronger with SE methods without filter paper, since the evaporation residue is confined to a smaller area than when a filter paper is used.

In this work, a relatively long gate delay of 2 µs was used. The gate delay was initially optimised for Li, Na, and K [25] and not further adjusted in this work to obtain comparable data. Ref. [45] showed that sensitivity is not significantly affected by increasing the gate delay but that precision is increased and self-absorption reduced by a longer gate delay. However, they used significantly shorter gate delays of 250 ns and 500 ns. Ref. [46] also recommend mitigating self-absorption by recording the signal with a longer gate delay, since this effect tends be more prominent in the early stages of laser-generated plasma.

Looking at the spectra of the gate delay investigations in [25], which were recorded similarly to the data within this study, it is noticeable that not only was the peak height affected by a change in gate delay at the same concentration (cf. Figure 11).There is also a clear broadening of the line at shorter gate delays (more intense grey values). With a longer gate delay, the peaks become significantly narrower and the effect of self-absorption decreases. This effect was observed for the three tested elements of Li, Na, and K.

Due to the strong self-absorption effects, future work will focus on the improvement of the method by the addition of a self-absorption correction to improve accuracy and compensate for the underestimation of higher predicted concentrations. When applying self-absorption correction, it may also be possible to have only one calibration curve instead of two or three for different concentration ranges. However, in this work, it was important to show that the method is basically applicable to natural waters and to determine the influencing factors. These seem to be determined less by the number of different elements than by self-absorption. In addition to filters to remove any undissolved components prior to analysis, a mobile hot plate to evaporate the micro droplets is required for future field application of the method.

The possibility to set up calibration curves for Zn with high coefficients of determination in standard solutions (cf. Table 3) proves that, in principle, it is also possible to analyse environmentally relevant elements in aqueous solutions with portable LIBS. In this work, no correlation between pLIBS and ICP-MS results for Zn could be found with the bottled mineral waters used. However, the test series was not very diverse for Zn, with all but one value below 0.1 mg/L in ICP-MS analyses. With an appropriate self-absorption correction and a diverse test series, Zn and possibly other problematic elements such as Pb and As should theoretically also be quantifiable.

It is clear that the documented analytical approach is not only applicable to single-element standard solutions but also to low mineralised natural waters with complex matrices. By adding a self-absorption correction, it should also be possible to quantitatively analyse more highly mineralised waters and improve the precision. As demonstrated, there is significant potential for developing field-based pLIBS for quantitative water analysis.

5. Conclusions

In our previous study, pLIBS was evaluated for the quantitative analysis of dissolved alkali metals in single-element standard solutions. The aim of this work was to show whether pLIBS can also be used for chemical compositional measurements of natural waters. The results of this study demonstrate that it is possible to quantitatively analyse low to medium mineralised bottled mineral waters with pLIBS for some of the main cations and anions. In higher mineralised waters with an EC above approximately 1000 µS/cm, the concentrations of the main cations and anions were mostly underestimated. This effect was mainly due to self-absorption, which was clearly visible in strong line broadening with increasing concentration. The effect of self-absorption was quite strong, despite a long gate delay being used, which should have compensated for high self-absorption. However, no self-reversal could be detected in any peak, which should have made self-absorption correction easier. There have been differences observed for singly ionised cations (alkali elements) compared to doubly ionised cations (alkaline earth metals). The self-absorption seems to have been pronounced for alkaline earth metals. Therefore, the analysis of alkali elements is currently more reliable than for alkaline earth metals, and the analysis of higher concentrations is more reliable for alkali elements. Analysis of anions is less reliable, even though LoDs may be calculated lower than for the other investigated ions. Of the anions, only Cl showed reasonably reliable results in natural waters. In general, the low detection limits are deceptive and do not reflect how well an EoI can be analysed. An analysable concentration range for natural mineral waters using the method described is approximately between 0.1 and 100 mg/L per element.

The next step in the development of the method is the introduction of an adapted self-absorption correction. It is quite promising that more elements will be calibratable (e.g., Zn). It should therefore be possible to analyse environmentally significant elements in the future. In any case, the ability to analyse natural mineral waters with complex matrices for their main ions opens up many new possibilities for pre-screening and on-site water analysis.