Temporal Evolution of Cooling by Natural Convection in an Enclosed Magma Chamber
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Physical and Geological Situation
2.2. Mathematical Model
2.3. Numerical Procedure
2.4. Mesh Study
3. Results
3.1. Validation
3.2. Results and Discussion
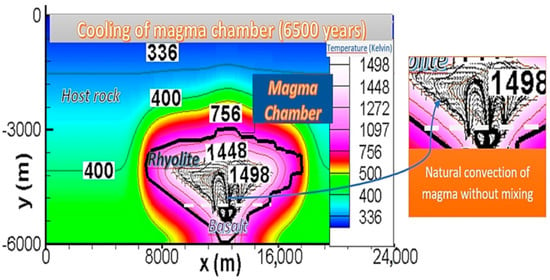
3.2.1. Temperature Results
3.2.2. Velocity Results
3.2.3. Concentration Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kavanagh, J.L.; Engwell, S.L.; Martin, S.A. A review of laboratory and numerical modelling in volcanology. Solid Earth 2018, 9, 531–571. [Google Scholar] [CrossRef] [Green Version]
- Pinkerton, H.; Sparks, R.S.J. Field measurements of the rheology of lava. Nature 1978, 276, 383–385. [Google Scholar] [CrossRef]
- Sparks, R.S.J.; Huppert, H.E.; Turner, J.S.; Sakuyama, M.; O’Hara, M.J. The Fluid Dynamics of Evolving Magma Chambers [and Discussion]. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1984, 310, 511–534. [Google Scholar] [CrossRef]
- Sonder, I.; Zimanowski, B.; Büttner, R. Non-Newtonian viscosity of basaltic magma. Geophys. Res. Lett. 2006, 33, 2–5. [Google Scholar] [CrossRef]
- Ryerson, F.J.; Weed, H.C.; Piwinskii, A.J. Rheology of subliquidus magmas. 1. Picritic compositions. J. Geophys. Res. 1988, 93, 3421–3436. [Google Scholar] [CrossRef]
- Shaw, H.R.; Wright, T.L.; Peck, D.L.; Okamura, R. The viscosity of basaltic magma; an analysis of field measurements in Makaopuhi lava lake, Hawaii. Am. J. Sci. 1968, 266, 225–264. [Google Scholar] [CrossRef]
- Spera, F.J. Thermal Evolution of Plutons: A Parameterized Approach. Science 1980, 207, 299–301. [Google Scholar] [CrossRef]
- Cashman, K.V.; Giordano, G. Calderas and magma reservoirs. J. Volcanol. Geotherm. Res. 2014, 288, 28–45. [Google Scholar] [CrossRef]
- Gudmundsson, A. Magma chambers: Formation, local stresses, excess pressures, and compartments. J. Volcanol. Geotherm. Res. 2012, 237–238, 19–41. [Google Scholar] [CrossRef]
- Shaw, H.R. Comments on viscosity, crystal settling, and convection in granitic magmas. Am. J. Sci. 1965, 263, 120–152. [Google Scholar] [CrossRef]
- Bartlett, R.W. Magma convection, temperature distribution, and differentiation. Am. J. Sci. 1969, 267, 1067–1082. [Google Scholar] [CrossRef]
- Eckert, E.R.G.; Goldstein, R.J.; Pfender, E.; Ibele, W.E.; Patankar, S.V.; Ramsey, J.W.; Simon, T.W.; Decker, N.A.; Kuehn, T.H.; Lee, H.; et al. Heat transfer—A review of 1987 literature. Int. J. Heat Mass Transf. 1988, 31, 2401–2488. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 9780470501979. [Google Scholar]
- Carrigan, C.R. The magmatic Rayleigh number and time dependent convection in cooling lava lakes. Geophys. Res. Lett. 1987, 14, 915–918. [Google Scholar] [CrossRef]
- Rabbanipour Esfahani, B.; Hirata, S.C.; Berti, S.; Calzavarini, E. Basal melting driven by turbulent thermal convection. Phys. Rev. Fluids 2018, 3, 053501. [Google Scholar] [CrossRef] [Green Version]
- Kaminski, E.; Jaupart, C. Laminar starting plumes in high-Prandtl-number fluids. J. Fluid Mech. 2003, 478, 287–298. [Google Scholar] [CrossRef] [Green Version]
- Clark, S.; Spera, F.J.; Yuen, D.A. Steady state double-diffusive convection in magma chambers heated from below. J. Fluid Mech. 1987, 289–305. [Google Scholar]
- Lesher, C.E.; Spera, F.J. Thermodynamic and Transport Properties of Silicate Melts and Magma. In The Encyclopedia of Volcanoes; Elsevier: Amsterdam, The Netherlands, 2015; pp. 113–141. ISBN 9780123859389. [Google Scholar]
- Cahn, R.W.; Haasen, P. Physical Metallurgy, 4th ed.; Elsevier Science: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Gutiérrez, F.; Parada, M.A. Numerical modeling of time-dependent fluid dynamics and differentiation of a shallow basaltic magma chamber. J. Petrol. 2010, 51, 731–762. [Google Scholar] [CrossRef] [Green Version]
- Cruden, A.R. On the emplacement of granites. J. Geol. Soc. London. 1998, 155, 853–862. [Google Scholar] [CrossRef]
- Agar, R.A. Copper mineralization and magmatic hydrothermal brines in the Rio Pisco section of the Peruvian coastal batholith. Econ. Geol. 1981, 76, 677–693. [Google Scholar] [CrossRef]
- Olivares, L.U.G. Conduction Plus Convection Heat Flow Modeling for the Linga Complex, Peruvian Coastal Batholith. Ph.D. Thesis, Loma Linda University, Loma Linda, CA, USA, 2017. [Google Scholar]
- Couch, R.; Whitsett, R.; Huehn, B.; Luis, B. Structures of the continental margin of Peru and Chile. Geol. Soc. Am. 1981, 703–726. [Google Scholar]
- Haederle, M.; Atherton, M.P. Shape and intrusion style of the Coastal Batholith, Peru. Tectonophysics 2002, 345, 17–28. [Google Scholar] [CrossRef]
- Lowell, R.P.; Kolandaivelu, K.; Rona, P.A. Hydrothermal Activity ☆. In Reference Module in Earth Systems and Environmental Sciences; Elsevier Inc.: Amsterdam, The Netherlands, 2014; pp. 1–19. ISBN 9780124095489. [Google Scholar]
- Ahlers, G.; Grossmann, S.; Lohse, D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection. Rev. Mod. Phys. 2009, 81, 503–537. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Du, K. A comprehensive review on the natural, forced, and mixed convection of non-Newtonian fluids (nanofluids) inside different cavities. J. Therm. Anal. Calorim. 2020, 140, 2033–2054. [Google Scholar] [CrossRef]
- Christiansen, E.B.; Craig, S.E. Heat transfer to pseudoplastic fluids in laminar flow. AIChE J. 1962, 8, 154–160. [Google Scholar] [CrossRef]
- Yoshinobu, A.S.; Okaya, D.A.; Paterson, S.R. Modeling the thermal evolution of fault-controlled magma emplacement models: Implications for the solidification of granitoid plutons. J. Struct. Geol. 1998, 20, 1205–1218. [Google Scholar] [CrossRef]
- Liu, L.; Lowell, R.P. Modeling heat transfer from a convecting, crystallizing, replenished silicic magma chamber at an oceanic spreading center. Geochem. Geophys. Geosyst. 2011, 12, 1–17. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Minkowycz, W.J., Sparrow, E.M., Eds.; Hemisphere Publishing Corporation: Washington, DC, USA, 1980. [Google Scholar]
- Frederick, L.; Moraga, S.G. Three-dimensional natural convection in finned cubical enclosures. Int. J. Heat Fluid Flow 2007, 28, 289–298. [Google Scholar] [CrossRef]
- Zemani, F.; Sabeur-bendehina, A.; Boussoufi, M. Numerical Investigation of Natural Convection in Air Filled Cubical Enclosure with Hot Wavy Surface and Partial Partitions. Procedia Comput. Sci. 2014, 32, 622–630. [Google Scholar] [CrossRef] [Green Version]
- Cherkaoui, A.S.M.; Wilcock, W.S.D.; Dunn, R.A.; Toomey, D.R. A numerical model of hydrothermal cooling and crustal accretion at a fast spreading mid-ocean ridge. Geochem. Geophys. Geosystems 2003, 4, 1–19. [Google Scholar] [CrossRef]
- Versteeg, H.M.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Limited, P.E., Ed.; Prentice Hall: Harlow, UK, 2007. [Google Scholar]
- Zambra, C.E.; Muñoz, J.F.; Moraga, N.O. A 3D coupled model of turbulent forced convection and diffusion for heat and mass transfer in a bioleaching process. Int. J. Heat Mass Transf. 2015, 85, 390–400. [Google Scholar] [CrossRef]
- Younis, O.; Pallares, J.; Grau, F.X. Transient natural convection cooling of a high Prandtl number fluid in a cubical cavity. Meccanica 2011, 46, 989–1006. [Google Scholar] [CrossRef]
- Fialko, Y.A.; Rubin, A.M. Thermal and mechanical aspects of magma emplacement in giant dike swarms. J. Geophys. Res. Solid Earth 1999, 104, 23033–23049. [Google Scholar] [CrossRef]
- Celentano, D.; Cruchaga, M.; Moraga, N.; Fuentes, J. Modeling Natural Convection with Solidification in Mould Cavities. Numer. Heat Transf. Part A Appl. 2001, 39, 631–654. [Google Scholar] [CrossRef]
- Kim, D.M.; Viskanta, R. Study of the effects of wall conductance on natural convection in differently oriented square cavities. J. Fluid Mech. 1984, 144, 153–176. [Google Scholar] [CrossRef]
- Dufek, J.; Bachmann, O. Quantum magmatism: Magmatic compositional gaps generated by melt-crystal dynamics. Geology 2010, 38, 687–690. [Google Scholar] [CrossRef]
- Cashman, K.; Sparks, R.S.J.; Blundy, J. Vertically extensive and unstable magmatic systems: A unified view of igneous processes. Volcanology 2017, 355, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martínez Ardila, A.M.; Clausen, B.L.; Memeti, V.; Paterson, S.R. Source contamination, crustal assimilation, and magmatic recycling during three flare-up events in the Cretaceous Peruvian Coastal Batholith: An example from the Ica-Pisco plutons. J. South Am. Earth Sci. 2019, 95, 102300. [Google Scholar] [CrossRef]
- Vidal, J.; Patrier, P.; Genter, A.; Beaufort, D.; Dezayes, C.; Glaas, C.; Lerouge, C.; Sanjuan, B. Clay minerals related to the circulation of geothermal fluids in boreholes at Rittershoffen (Alsace, France). J. Volcanol. Geotherm. Res. 2018, 349, 192–204. [Google Scholar] [CrossRef]
- Lesher, C.E.; Hervig, R.L.; Tinker, D. Self diffusion of network formers (silicon and oxygen) in naturally occurring basaltic liquid. Geochim. Cosmochim. Acta 1996, 60, 405–413. [Google Scholar] [CrossRef]
- Huppert, H.E.; Sparks, R.S.J. restrictions on the compositions of mid-ocean ridge basalts: A fluid dynamical investgation. Nature 1980, 286, 46–48. [Google Scholar] [CrossRef]
- Huppert, H.E.; Stewart Turner, J.J.; Sparks, R.S. Replenished magma chambers: Effects of compositional zonation and input rates. Earth Planet. Sci. Lett. 1982, 57, 345–357. [Google Scholar] [CrossRef] [Green Version]
- Huppert, H.E.; Sparks, R.S.J. Double-diffusive convection due to crustallization in magmas. Annu. Rev. Earth Planet. Sci. 1984, 12, 11–37. [Google Scholar] [CrossRef]
- Ferré, E.C.; Maes, S.M.; Butak, K.C. The magnetic stratification of layered mafic intrusions: Natural examples and numerical models. Lithos 2009, 111, 83–94. [Google Scholar] [CrossRef]









| Transport Properties | Magma [18] | Host Rock [30] | Param. | Param. | ||
|---|---|---|---|---|---|---|
| 2600 | 2670 | 1.62 × 1017 | Pr | 2.42 × 105 | ||
| 1450 | 1000 | 75 | Le | 5.3 × 104 | ||
| 0.6 | 2.65 | 7426 | Tf,0 (K) | 1498 | ||
| 1.6 × 10−7 | 9.93 × 10−7 | 0.4 | Tref (K) | 1473 | ||
| * | 5 × 10−5 | - | 1.01 × 10−2 | Cs,0 | 0.5 | |
| 100 | - | 2.19 × 1013 | Cf,0,a | 0.47 | ||
| 3 × 10−12 | - | 1.41 × 10−3 | Cf,0,b | 0.7 |
| Mesh | Nodes X × Y | Total Nodes | N° Nodes in Chamber Zone | N° Nodes in Host Rock | RE | t (s) |
|---|---|---|---|---|---|---|
| 1 | 300 × 90 | 27,000 | 2800 | 24,200 | 0 | 13,180 |
| 2 | 280 × 70 | 19,600 | 2450 | 17,150 | 0.0078 | 9836 |
| 3 | 196 × 58 | 11,368 | 2450 | 8918 | 0.1283 | 4393 |
| 4 | 156 × 60 | 9360 | 1800 | 7560 | 1.1756 | 3440 |
| 5 | 130 × 50 | 6500 | 1250 | 5250 | 2.0933 | 2960 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zambra, C.E.; Gonzalez-Olivares, L.; González, J.; Clausen, B. Temporal Evolution of Cooling by Natural Convection in an Enclosed Magma Chamber. Processes 2022, 10, 108. https://doi.org/10.3390/pr10010108
Zambra CE, Gonzalez-Olivares L, González J, Clausen B. Temporal Evolution of Cooling by Natural Convection in an Enclosed Magma Chamber. Processes. 2022; 10(1):108. https://doi.org/10.3390/pr10010108
Chicago/Turabian StyleZambra, Carlos Enrique, Luciano Gonzalez-Olivares, Johan González, and Benjamin Clausen. 2022. "Temporal Evolution of Cooling by Natural Convection in an Enclosed Magma Chamber" Processes 10, no. 1: 108. https://doi.org/10.3390/pr10010108
APA StyleZambra, C. E., Gonzalez-Olivares, L., González, J., & Clausen, B. (2022). Temporal Evolution of Cooling by Natural Convection in an Enclosed Magma Chamber. Processes, 10(1), 108. https://doi.org/10.3390/pr10010108