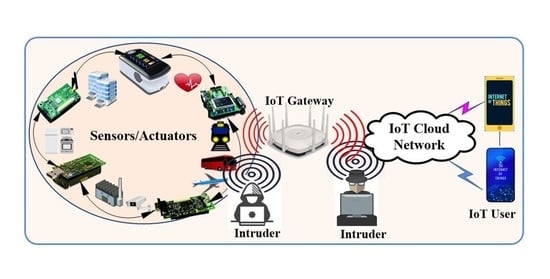
Unforgeable Digital Signature Integrated into Lightweight Encryption Based on Effective ECDH for Cybersecurity Mechanism in Internet of Things
Abstract
:1. Introduction
1.1. Research Problem Statement
1.2. Research Contribution
- It proposes an efficacious digital signature, which confirms the true identity of the sender with certainty using a hash function and the three steps of curve-point inspection based on the ECDH scheme.
- It proposes a secure combination between encryption and digital signature, and it studies the weaknesses of other combinations.
- It proposes a lightweight encryption mechanism that can resolve the weak bit problems in the shared secret key due to the Diffie–Hellman exchange.
- It proposes secure key distribution among a group of IoT devices that can confidentially transfer a shared secret over an insecure communication channel. The shared group secret key (SGSK) is an ephemeral (dynamic) entity and is calculated on the basis of the ECDH scheme. Moreover, perfect forward secrecy, which is recommended by the RFC8442 standard, can be achieved using the ephemeral shared key.
- A comprehensive probabilistic mathematical cryptanalysis using the random oracle model (ROM) is employed to prove the security of the proposed digital signature and the encryption in the IoT.
- Finally, several simulation experiments have been conducted to evaluate the performance of the proposed mechanisms in terms of processing time, storage cost, and energy consumption. Overall, the proposed system offers faster processing times, less memory and energy consumption, and an effective method of key distribution.
2. Related Works on Encryption and Digital Signature
- The new proposed combination between digital signature and encryption has the ability to verify the true identity of the sender and receiver, which is considered the main function of the digital certificate in [17].
- The verification process in the establishment the digital certificate necessitates tedious work, consumes excessive power, and introduces extra processing delay if used in the IoT platform.
- The QoS performance of the proposed algorithm outperforms the QoS performance of the digital certificate in [17]. This is mainly due to the fact that the digital certificate authority, which is responsible for verifying the digital certificate, consumes excessive power and increases the end-to-end delay as will be explained in Section 5.
2.1. Lightweight Digital Signatures on IoT
2.2. Lightweight Encryption Algorithms on IoT
3. System Design of the ELCD Algorithm
- The IoT gateway has a strong security protection system, and it is extremely hard to compromise.
- Each IoT device (sensor, actuator, remote IoT user, etc.) has two secure keys: a public key, which is available to all involved IoT devices, and a private key, which is not known publicly.
- The domain parameters of the ECDH are embedded and uploaded into all IoT devices during the programming session, which means that the ELCD mechanism is very suitable in industrial IoT (IIoT) applications.
3.1. The Key Management Algorithm
- Shared Group Secret Key (SGSK)
- IoT_D1 creates the first part of the group public key as Q1 = d1 G.
- IoT_D1 sends Q1 to the next IoT_D (e.g., IoT_D2), which creates the second part of the group public key as Q12 = d2 Q1.
- This scenario continues until the last IoT_D (e.g., IoT_D5) receives the previous parts of the group public key (Q1234), which is considered as the total group public key created at IoT_D5 (QT5 = Q1234). The total group public key at IoT_D number v can be generalized for any number of nodes in the group as:where N represents the total number of IoT_D in the group. For example, we can calculate QT3 based on five IoT_Ds as d1 d2 d4 d5 G.
- ▪
- Finally, the SGSK can be calculated at the IoT_D number v as (XK, YK) = dv QTv. For example, the SGSK at IoT_D number 3 can be calculated as d3 QT3 while the SGSK at IoT_D number 4 can be calculated as d4 QT4. It is interesting to note that d3 QT3 = d4 QT4, because d3 QT3 = d3 d1 d2 d4 d5 G = d4 d1 d2 d3 d5 G = d4 QT4. Each IoT_D should verify the received QTv before performing any calculation. Therefore, if a malicious node exists during the key distribution phase, it does not know the domain parameters (i.e., n and G) and then it cannot calculate the appropriate QTv. Therefore, each IoT device must receive QTv before creating the SGSK and performing the digital signature and cryptographic algorithms.
3.2. The Lightweight Encryption Algorithm
- Calculate the curve point Pb(X1, Y1) = E G, which is hard to reverse because the scalar multiplication in the ECC has a one-way function property.
- Calculate the ciphertext C = (m X1) mod n, where m is obtained by converting M to an integer number using a padding scheme, which should be an agreed-upon reversible protocol. In this paper, each M has been parsed to multiple chunks based on the message size in an elliptic curve (e.g., Secp192r1) [34]. This means that the maximum length of each chunk is 127 bytes, and the minimum length is 24 bytes.
- Calculate E = StrToInt(Hash(XK)), where Hash represents the corresponding cryptographic hash used in the authentication code calculation.
- Calculate the curve point Pb(X1, Y1) = E G.
- Calculate the integer number of the chunk m = (C X1−1) mod n, where X1−1 mod n can be resolved using a modular multiplicative inverse.
- Convert the integer number m to the parse (i) of plaintext (M), where i is the parse number. The concatenation of all parses should recreate the original message M.
3.3. The Proposed Digital Signature Algorithm
- Phase 1, Create Digest.
- Phase 2, Create DS.
- (1)
- Encrypt the digest with the sender private key dS to calculate the digital signature as DS = (dS−1 YK Z) mod n, where YK represents the y-coordinate of the shared secret key.
- (2)
- Since dS is a random number (ephemeral) that changes every session, DS also changes in each session.
- Phase 3, Encrypt Message with DS.
- (1)
- Encrypt the concatenation of m and DS with the shared secret key XK. The proposed lightweight encryption algorithm is used to encrypt (m + DS), and the final output is the ciphertext (C).
- (2)
- Calculate E = StrToInt(Hash(XK)).
- (3)
- Calculate the curve point Pb(X1, Y1) = E G.
- (4)
- Calculate C = ((m + DS) X1) mod n.
- Phase 4, Decrypt Cyphertext.
- (1)
- Calculate E = StrToInt(Hash(XK)).
- (2)
- Calculate the curve point Pb(X1, Y1) = E G.
- (3)
- Calculate the concatenation of m and DS: (m + DS) = (C X1−1) mod n.
- Phases 5 and 6, DS Verification and Obtaining the Message.
- (1)
- Verify the true identity of the sender that is used in signing the plaintext (YK) using three steps of curve-point inspection: 1. Check that QS is not equal to the identity element O, 2. Check that QS lies on the curve 3. Check that n QS = O.
- (2)
- Retrieve the digest from the received DS as U1 = (DS YK−1 QS) = Z G. This works because (DS YK−1) QS = ((dS−1 YK Z) YK−1 (dS G) = Z G, since the product of an element’s inverse and the element itself is the identity.
- (3)
- Create the digest for the received m as Z- = StrToInt(Hash(m)) mod n.
- (4)
- If the created Z- G = the received Z G, the received DS is valid, otherwise the received DS is invalid.
- (5)
- If the received DS is valid, accept the received message m and covert it back to M.
- (a)
- Domain parameters are not publicly exchanged between IoT devices; rather, they are uploaded into all devices during the programming session. This means that the attacker cannot create a valid public key Q.
- (b)
- The verification of DS in the proposed method can verify the true identity with certainty. This means that the attacker needs to solve the elliptic curve discrete logarithm problem (ECDLP), which makes it extremally hard to reverse DS and obtain the private key for making a fake private key.
- (c)
- The padded message m is hashed and digitally signed using the ECC and inverse modular multiplication of the sender private key, which is considered extremely hard to reverse and obtain the original message from.
- (d)
- More importantly, the CMA hash function [24] creates a random digest for any two similar input messages. This is mainly due to the fact that the CMA is designed based on a time-enhanced-based one-time password (TEOTP) and it includes a salt random string to create the random digest for similar inputs.
4. Cybersecurity Analysis
4.1. Adversary Model for ELCD on the IoT
- Spoofing attack: The adversary intercepts or eavesdrops on IoT network traffic to obtain an IoT device’s credential, which is used to gain access to the sensed information.
- A man-in-the-middle attack: The malicious adversary has the ability to listen to all traffic on a network and initiate a connection with any IoT devices. Furthermore, if the adversary acts as an active man-in-the-middle, it can modify the content of captured messages and resend them to the recipient.
- A replay attack: Instead of sending a message directly to the recipient, a replay attack makes a copy of that message and then uses it later. This is carried out by an adversary who intercepts the messages and delays, replays, or retransmits those messages.
- A brute force attack: The malicious adversary tries every possible mixture of letters, numbers, and characters to crack the shared secret key even if the domain parameters that are used in the ECDH scheme by both parties are extremely hard to obtain.
- A sensor capture attack: The impostor adversary captures a sensor node and steals the domain parameters and shared secret key to implement illegal actions on the IoT network.
- A stolen-verifier attack: The impostor adversary who has stolen the shared secret key from an IoT device can pretend to be an authorized device in order to launch attacks against other IoT devices, steal data, or bypass access controls.
4.2. Cryptoanalysis of ELCD
- Chosen plaintext attack (CPA): The adversary is assumed to obtain the ciphertexts for any plaintexts of their choice. Moreover, the adaptive CPA (CPA2) means that the adversary has the ability to choose the new input to the encryption of ELCD (ELCDE) based on the analysis of her/his previously selected plaintext queries and their corresponding ciphertexts [38]. The definition of CPA can be represented mathematically by assuming that an adversary A gains access to an encryption oracle with any pair of equal-length messages (m1, m2) as input. The oracle returns a ciphertext as output.
- Chosen ciphertext attack (CCA): The adversary is assumed to obtain the decryption of any ciphertext(s) of their choice. Moreover, the adaptive CCA (CCA2) means that the adversary has the ability to choose the new input to the decryption of ELCD based on the analysis of her/his previously selected queries [39].
4.3. The ELCD Cybersecurity Analysis
4.3.1. Proven Security for ELCD in the Random Oracle Model
- Methodology of Proof: The contradiction methodology is used to prove Theorem 1. Let us assume an adversary A that runs in PPT exists, who breaks the security of ELCDE. The algorithm A constructs a PPT distinguisher B that distinguishes the output of Pb from a random number with non-negligible cost. Since Pb is PRF; this contradicts the previous conclusion that Pb is a random function. Therefore, the original assumption is false and the ELCDE must be secure.
- Methodology of Proof: The adversary guessing methodology is used to prove Theorem 2. Let us assume A is a PPT adversary algorithm that breaks ELCDE in the sense of IND-CCA for which . To break ELCDE, A gains access to an encryption oracle with any pair of equal-length messages (m0, m1) as input. The encryption oracle (mb) takes this input, and returns an encryption of either (m0, m1). The goal of A is to determine the value of b. If A guesses correctly, then ELCDE is not secure, otherwise ELCDE is secure against IND-CCA.
4.3.2. Proven Security for Proposed Digital Signature in ROM
- Method 1: Encrypt-and-Sign (EAS), which means that data should be encrypted using K1 as C = Ek1(M) and the digital signature should be calculated using K2 as D = DSk2(M). The sending message is the pair (C, D) that should be sent separately.
- Method 2: Sign-then-encrypt (STE), which means that D is first calculated, and then the original data and D are concatenated and encrypted together. The sending message is C = Ek1(M + D), where D = DSk2(M).
- Method 3: Encrypt-then-Sign (ETS), which means the original data M is first encrypted using K1 as C = Ek1(M), and then the D is calculated over C. The sending message is the pair (C, D), where D = MACk2(C).
- Methodology of Proof: The proof of Theorem 3 is divided into two parts: the proof that ELCDDS is (t, qϵ)-secure against adaptive CPA, and the proof ELCD = ( , , , ) created using DS-then-encrypt is a secure combination between ELCDE and ELCADS. The contradiction methodology is used to prove the two parts of Theorem 3. The methodology of the first proof part of Theorem 3 can be described as follows:
- Assume an adversary A that runs in PPT exists, who has the ability to generate a forgery digital signature for the original message M with a probability .
- If the probability is proven not negligible, this means that A is doing well and ELCDDS is not secure.
- However, if the probability is proven negligible, this means A is not doing well and ELCDDS should be secure.
- B chooses a random index i* ∈ {1, …, q}.
- B can only have one query for the random oracle H.
- B receives the ith query from A to H and responses as follows:
- ○
- Let mi represent the ith query from A to H: if i = i*, this means mi = m and H will return ; otherwise, H chooses a random ri←.
- ○
- Calculate Outi = , return Outi.
- ▪
- If A sends a signature request query on message m, B chooses i such that mi= m; if i = i*, abort; otherwise, return ri as the signature.
- ▪
- When A generates its forgery (m, σ), if m = mi* then B outputs σ; otherwise, abort.
- Methodology of Second Part Proof: The methodology of proof the second part of Theorem 3 can be described as follows:
- Assume the existence of adversary A that gains access to three random oracle functions: sign oracle function (SOF), encryption oracle function (EOF) and decryption oracle function (DOF). The three functions simulate ELCADS and ELCDE.
- First, A queries SOF with any pair of equal-length messages (m0, m1) as input. The output of SOF is a pair of bits (, ).
- Second, A flips a single bit in either (, ). Let us assume that the single bit of has been flipped to be .
- Third, A queries EOF with a pair of equal-length digital signatures (, ). The output of EOF is a pair of (, ) = .
- Fourth, A flips a single bit in at the same position that was flipped in to obtain . After that, A queries DOF with .
- The goal of A is to determine the value of b. If A guesses correctly, then combination between ELCDE and ELCADS in ELCD is not secure, otherwise it is secure against IND-CCA.
4.4. Countermeasures against Replay and Man-in-the-Middle Attacks
- The sender authentication based on YK in the digital signature should be checked before processing a message from a man-in-the-middle attacker.
- The digital signature is calculated based on the private key of the sender, which is protected by a hash function and encryption after a digital signature is applied to the plaintext.
- Replay attacks need to implement three steps before resending the intercepted message. These steps are shared secret key calculation, digital signature, and message encryption, which are very difficult to gain access to without breaching the hash function and the shared secret key.
4.5. Countermeasures against Brute Force Attacks
4.6. Countermeasures against Session Hijacking and Spoofing Attacks
4.7. Countermeasures against Device Capture and Stolen-Verifier Attacks
5. Implementation and Performance Evaluation of ELCD on the IoT
- The size of encryption and authentication keys is 24 bytes (192 bits) and the experimental processing latency that has been estimated for the ECDH to create and exchange the secret key is 0.576 s [28].
- The optimally recognized algorithm for resolving the k-size of ECDLP requires 0.886 ∗ steps. Generally, a k-bit security strength can be achieved if the security system practices at least 2 × k-bit key size. Therefore, ELCD prefers to use the Secp192r1 curve, which can provide 96-bit security strength [34,40].
- The maximum message size of the IoT device is 127 bytes and it can be implemented based on the 6LowPAN protocol (40 bytes header), which is used to create a connection association between the IoT device and the sensor nodes [41].
5.1. Performance Evaluation and Results Discussion
5.1.1. Performance Comparison between ELCD Digital Signature and Baseline Algorithms
5.1.2. Performance Comparison between ELCD Cryptographic and Baseline Algorithms
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sarker, I.H.; Khan, A.I.; Abushark, Y.B.; Alsolami, F. Internet of Things (IoT) Security Intelligence: A Comprehensive Overview, Machine Learning Solutions and Research Directions. Mob. Netw. Appl. 2022, 1–17. [Google Scholar] [CrossRef]
- Sciancalepore, S.; Piro, G.; Vogli, E.; Boggia, G.; Grieco, L.; Cavone, G. LICITUS: A lightweight and standard compatible framework for securing layer-2 communications in the IoT. Comput. Netw. 2016, 108, 66–77. [Google Scholar] [CrossRef] [Green Version]
- Kittur, A.S.; Pais, A.R. A trust model based batch verification of digital signatures in IoT. J. Ambient. Intell. Humaniz. Comput. 2019, 11, 313–327. [Google Scholar] [CrossRef]
- Li, S.; Zhang, T.; Yu, B.; He, K. A Provably Secure and Practical PUF-Based End-to-End Mutual Authentication and Key Exchange Protocol for IoT. IEEE Sens. J. 2021, 21, 5487–5501. [Google Scholar] [CrossRef]
- Arne, B.; Le, N.; Dominik, S.; Stephan, S.; Lars, C.W. Security Properties of Gait for Mobile Device Pairing. IEEE Trans. Mob. Comput. 2019, 19, 697–710. [Google Scholar]
- Diro, A.A.; Chilamkurti, N.; Kumar, N. Lightweight Cybersecurity Schemes Using Elliptic Curve Cryptography in Publish-Subscribe fog Computing. Mob. Netw. Appl. 2017, 22, 848–858. [Google Scholar] [CrossRef]
- Khasawneh, S.; Kadoch, M. Hybrid Cryptography Algorithm with Precomputation for Advanced Metering Infrastructure Networks. Mob. Netw. Appl. 2018, 23, 982–993. [Google Scholar] [CrossRef]
- Bu, L.; Isakov, M.; Kinsy, M.A. A secure and robust scheme for sharing confidential information in IoT systems. Ad Hoc Netw. 2019, 92, 101762. [Google Scholar] [CrossRef] [Green Version]
- Hendaoui, F.; Eltaief, H.; Youssef, H. UAP: A unified authentication platform for IoT environment. Comput. Netw. 2021, 188, 107811. [Google Scholar] [CrossRef]
- Vidya, R.; Prema, K.V. Lightweight hashing method for user authentication in Internet-of-Things. Ad Hoc Netw. 2019, 89, 97–106. [Google Scholar]
- Chuang, Y.-H.; Lo, N.-W.; Yang, C.-Y.; Tang, S.-W. A Lightweight Continuous Authentication Protocol for the Internet of Things. Sensors 2018, 18, 1104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Fuentes, J.M.; Gonzalez-Manzano, L.; Lopez, J.; Peris-Lopez, P.; Choo, K.-K.R. Editorial: Security and Privacy in Internet of Things. Mob. Netw. Appl. 2019, 24, 878–880. [Google Scholar] [CrossRef]
- Riad, K.; Huang, T.; Ke, L. A dynamic and hierarchical access control for IoT in multi-authority cloud storage. J. Netw. Comput. Appl. 2020, 160, 102633. [Google Scholar] [CrossRef]
- Alexander, J.M.; Kueffer, C.; Daehler, C.; Edwards, P.J.; Pauchard, A.; Seipel, T.; Arévalo, R.J.; Cavieres, L.A.; Dietz, H.; Jakobs, G.; et al. NETRA: Enhancing IoT Security Using NFV-Based Edge Traffic Analysis. IEEE Sens. J. 2019, 19, 4660–4671. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.; Han, L.; Lu, H.; Fu, C. Intrusion Detection System for IoT Heterogeneous Perceptual Network. Mob. Netw. Appl. 2021, 26, 1461–1474. [Google Scholar] [CrossRef]
- Alamer, A. An efficient group signcryption scheme supporting batch verification for securing transmitted data in the Internet of Things. J. Ambient. Intell. Humaniz. Comput. 2020, 1–18. [Google Scholar] [CrossRef]
- Ahmed, A.A. Lightweight Digital Certificate Management and Efficacious Symmetric Cryptographic Mechanism over Industrial Internet of Things. Sensors 2021, 21, 2810. [Google Scholar] [CrossRef]
- Johnson, D.; Menezes, A.; Vanstone, S. The elliptic curve digital signature algorithm (ECDSA). Int. J. Inf. Secur. 2001, 1, 36–63. [Google Scholar] [CrossRef]
- Mughal, M.A.; Luo, X.; Ullah, A.; Ullah, S.; Mahmood, Z. A lightweight digital signature based security scheme for human-centered Internet of Things. IEEE Access 2018, 6, 31630–31643. [Google Scholar] [CrossRef]
- Park, C. A Secure and Efficient ECQV Implicit Certificate Issuance Protocol for the Internet of Things Applications. IEEE Sens. J. 2017, 17, 2215–2223. [Google Scholar] [CrossRef]
- Mohseni-Ejiyeh, A.; Ashouri-Talouki, M.; Mahdavi, M. An Incentive-Aware Lightweight Secure Data Sharing Scheme for D2D Communication in 5G Cellular Networks. ISeCure 2018, 10, 15–27. [Google Scholar]
- Abro, A.; Deng, Z.; Memon, K.A. A Lightweight Elliptic-Elgamal-Based Authentication Scheme for Secure Device-to-Device Communication. Future Internet 2019, 11, 108. [Google Scholar] [CrossRef] [Green Version]
- Javed, Y.; Khan, A.S.; Qahar, A.; Abdullah, J. EEoP: A lightweight security scheme over PKI in D2D cellular networks. J. Telecommun. Electron. Comput. Eng. 2017, 9, 99–105. [Google Scholar]
- Ahmed, A.A.; Ahmed, W.A. An Effective Multifactor Authentication Mechanism Based on Combiners of Hash Function over Internet of Things. Sensors 2019, 19, 3663. [Google Scholar] [CrossRef]
- Sciancalepore, S.; Piro, G.; Boggia, G.; Bianchi, G. Public Key Authentication and Key Agreement in IoT Devices with Minimal Airtime Consumption. IEEE Embed. Syst. Lett. 2017, 9, 1–4. [Google Scholar] [CrossRef] [Green Version]
- NIST Computer Security Resource Center. Lightweight Cryptography Project. Available online: https://csrc.nist.gov/projects/lightweight-cryptography (accessed on 27 November 2022).
- Seok, B.; Sicato, J.C.S.; Erzhena, T.; Xuan, C.; Pan, Y.; Park, J.H. Secure D2D Communication for 5G IoT Network Based on Lightweight Cryptography. Appl. Sci. 2020, 10, 217. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.; Quasim, M.T.; Alghamdi, N.S.; Khan, M.Y. A Secure Framework for Authentication and Encryption Using Improved ECC for IoT-based Medical Sensor Data. IEEE Access 2020, 8, 52018–52027. [Google Scholar] [CrossRef]
- Muhammad, U.; Ahmed, I.; Imran, M.A.; Shujaat, K.; Usman, A.S. SIT: A lightweight encryption algorithm for secure internet of things. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 402–411. [Google Scholar]
- Shah, R.H.; Salapurkar, D.P. A multifactor authentication system using secret splitting in the perspective of Cloud of Things. In Proceedings of the International Conference on Emerging Trends & Innovation in ICT (ICEI), Pune, India, 3–5 February 2017; pp. 1–4. [Google Scholar]
- Hammi, B.; Fayad, A.; Khatoun, R.; Zeadally, S.; Begriche, Y. A Lightweight ECC-Based Authentication Scheme for Internet of Things (IoT). IEEE Syst. J. 2020, 14, 3440–3450. [Google Scholar] [CrossRef]
- Rangwani, D.; Sadhukhan, D.; Ray, S.; Khan, M.K.; Dasgupta, M. A robust provable-secure privacy-preserving authentication protocol for Industrial Internet of Things. Peer-to-Peer Netw. Appl. 2021, 14, 1548–1571. [Google Scholar] [CrossRef]
- NIST. Fips Publication 180-2: Secure Hash Standard; Technical Report; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2003.
- Lochter, M.; Merkle, J. RFC 5639: Elliptic Curve Cryptography (ECC) Brainpool Standard Curves and Curve Generation; IETF: Fremont, CA, USA, 2010. [Google Scholar]
- Li, X.; Niu, J.W.; Ma, J.; Wang, W.D.; Liu, C.L. Cryptanalysis and improvement of a biometrics-based remote user authentication scheme using smart cards. J. Netw. Comput. Appl. 2011, 34, 73–79. [Google Scholar] [CrossRef]
- Wang, J.; Han, K.; Alexandridis, A.; Zilic, Z.; Pang, Y.; Wu, W.; Jeon, G. A novel security scheme for Body Area Networks compatible with smart vehicles. Comput. Netw. 2018, 143, 74–81. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, G.; Li, T.; Li, F.; Tian, Y.; Yu, X. Belief and fairness: A secure two-party protocol toward the view of entropy for IoT devices. J. Netw. Comput. Appl. 2020, 161, 102641. [Google Scholar] [CrossRef]
- Biryukov, A. Adaptive Chosen Plaintext Attack. In Encyclopedia of Cryptography and Security; Van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA, USA, 2011. [Google Scholar]
- Biryukov, A. Related Key Attack. In Encyclopedia of Cryptography and Security; Van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA., USA, 2011. [Google Scholar]
- Silverma, J.H. An Introduction to the Theory of Elliptic Curves, Summer School on Computational Number Theory and Applications to Cryptography; Brown University: Providence, RI, USA, 2006. [Google Scholar]
- IPv6 over Low-Power Wireless Personal Area Networks (6LoWPANs): Overview, Assumptions, Problem Statement, and Goals. Available online: http://www.ietf.org/rfc/rfc4919.txt (accessed on 27 November 2022).
- Mininet-IoT Emulator of Internet of Things. Available online: https://github.com/ramonfontes/mininet-iot (accessed on 27 November 2022).
- A Security Site. Available online: https://asecuritysite.com/encryption (accessed on 27 November 2022).
- Ahmed, A.A. An optimal complexity H. 264/AVC encoding for video streaming over next generation of wireless multimedia sensor networks. Signal Image Video Process. 2016, 10, 1143–1150. [Google Scholar] [CrossRef]









| Notation | Meaning | Notation | Meaning |
|---|---|---|---|
| C | Ciphertext | M | Plaintext message |
| CCA | Chosen cipher attack | m | The integer number of M |
| CPA | Chosen plaintext attack | n | Order of G |
| d | Private key | O | An extra point at infinity of the curve |
| D | Destination node | P | Modular prime |
| DS | Digital signature | Pb | Random point in the curve |
| ECC | Elliptic curve cryptography | Pb.X1 | X coordinate of Pb |
| ECDH | Elliptic curve Diffie–Hellman | Q | Public key |
| ELCD | Effective, lightweight cryptographic and digital signature | S | Source node |
| G | Base point generator | SGSK | Shared group secret key |
| Approaches | Year of Publication | Methodology and Features | Limitations |
|---|---|---|---|
| ECDSA [18] | 2001 | Proposed an elliptic curve-based digital signature algorithm. | Slowness, design flaws, and insufficiently defensive. |
| SCDSA and MPS-SCDSA [19] | 2018 | Secured communication between smart devices in IoT. | Needs high processing resource and consumes extra energy. |
| C.S. Park et al. [20] | 2018 | Proposed an enhanced version of the elliptic curve Qu–Vanstone (ECQV) certificate issuance protocol. | Consumes more power and latency due to verification of certificate at the certificate authority. |
| Adeel et al. [22] | 2019 | Merged two algorithms: ECC to manage public key infrastructure (PKI), and ElGamal to implement encryption. | Lacks adversary mode analysis. |
| Yasir et al. [23] | 2017 | Developed a tiny cryptographic system that depends on ECC and ElGamal. | The cryptanalysis was not studied. |
| KMP [25] | 2017 | Integrated the ECDH exchange with a digital certificate to authenticate the key generation. | Does not fit IoT resource-constrained limitations due to power consumption of implied certificate. |
| B. Seok et al. [27] | 2020 | Proposed a secure device-to-device communication using the idea of AEAD and ECC to fit an IoT resource-constrained system. | The cryptanalysis was not studied. |
| M. Ayoub et al. [28] | 2020 | Developed a secure ECC based authentication and encryption that utilizes user credentials and biometric parameters to improve user authentication. | Does not fit IoT resource-constrained limitations due to vulnerability to error of biometric parameters. |
| SIT [29] | 2017 | Used the idea of combining Feistel 64-bit key and a uniform substitution permutation. | Does not fit IoT resource-constrained limitations due to power consumption. |
| Shah et al. [30] | 2017 | Combined the authentication and the cryptography based on Diffie–Hellman to distribute a secret key among IoT devices. | Does not prove the security of the combination. |
| B. Hammi et al. [31] | 2020 | Proposed OTP that relies on elliptic curve cryptography and isogeny. | The randomness of the OTP based on ECC is not ensured. |
| ELCD at IoT Sender (S) | |
|---|---|
| Input: Secp192r1 domain parameters p, a, b, G, n, h; | |
| Output: QS, DS, C;//QS: public key of S, DS: digital signature; C: ciphertext | |
| Start Algorithm (ELCD) | |
| 1 | | While (new session start) do |
| 2 | | Pick private key (dS);//1 ≤ dS ≤ n |
| 3 | | QS = (dS G); |
| 4 | | Send_Public_key (QS);//Send the public key to destination |
| 5 | | Receive_Public_key(QD);//Receive the public key of D |
| 6 | | K(XK,YK) = dS QD;//calculate the shared key |
| Phase 1, Create Digest | |
| 7 | | m = StrToInt(M);//convert the plaintext to an integer. |
| 8 | | Z = StrToInt(Hash(m)) mod n;//hash fun. for integer m |
| Phase 2, Create DS | |
| 9 | | if (m is the first message) //first message of the session |
| 10 | | DS = (dS−1 YK Z) mod n;//DS: digital signature |
| Phase3, Encrypt (m + DS) | |
| 11 | | E = StrToInt(Hash(XK)) mod n;//E: the hash fun. of key XK |
| 12 | | Pb(X1,Y1) = E G; |
| 13 | | C = ((m + DS) X1) mod n;//C: the ciphertext |
| 14 | | Send(“C”);//The source sends “C” only to D |
| 15 | | End;//if Statement |
| 16 | | End;//While loop |
| 17 | End;//Algorithm |
| ELCD at IoT Receiver (D) | |
| Input: Secp192r1 domain parameters p, a, b, G, n, h; | |
| Output: QD, DS, C;//QD: Public key of D | |
| 18 | Start Algorithm (ELCD) |
| 19 | | While (new session start) do |
| 20 | | Pick private key (dD);//1 ≤ dD ≤ n |
| 21 | | QD = (dD G); |
| 22 | | Send_Public_key (QD);//Send the public key to source node |
| 23 | | Receive_Public_key(QS);//Receive the public key from S |
| 24 | | K(XK,YK) = dD QS; //if QS is a valid curve point, the shared key will be calculated |
| 25 | | Foreach (C received and Flag == true) do |
| 26 | | if (first message received) //Receive the first message |
| Phase 4, Decrypt C | |
| 27 | | Get(C);//Receive the ciphertext (C) |
| 28 | | E = StrToInt(Hash(XK)) mod n; |
| 29 | | Pb(X1,Y1) = E G; |
| 30 | | m + DS = (C X1−1) mod n; |
| Phase 5 and 6, DS Verification & Obtain Message | |
| 31 | | Verify_Public_key(QS);//Receiver will verify QS |
| 32 | | U1 = (DS YK−1 QS) = Z G mod n; |
| 33 | | Z- = StrToInt(Hash(m)) mod n;//Z- is digest for rec. m |
| 34 | | if (U1 == Z- G) |
| 35 | | The signature is valid, and the source is legitimate; |
| 36 | | Get(m);//Obtain the m and |
| 37 | | else |
| 38 | | The signature is invalid, and the source is illegitimate; |
| 39 | | Flag = false; |
| 40 | | End;// if Statement |
| 41 | | else |
| 42 | | E = Hash(XK) mod n; |
| 43 | | Pb(X1,Y1) = E G; |
| 44 | | m = (C X1−1) mod n; |
| 45 | | End;// if Statement |
| 46 | | M = Convert_IntToStr(m);//convert m to M. |
| 47 | | End;// for loop |
| 48 | | End;//While loop |
| 49 | End;//Algorithm |
| Parameter | Values |
|---|---|
| MAC and PHY | 802.15.14_hmsim and 802.11_hmsim |
| Propagation model | Shadowing |
| Path loss exponent | 3.0 |
| Shadowing deviation (dB) | 3.0 |
| Event area | (1000 m × 900 m) |
| Cover of IoT device | 150 m |
| Cover range of BaseST1 | 250 m |
| Traffic emulator | TCP Socket client/server; 1000 messages. |
| Performance metrics | CPU execution time, storage cost, and energy consumption |
| ECDH curve | Secp192r1 |
| Message size | 127 bytes |
| Key size | 192 Bits |
| Emulation duration | 1000 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.A.; Barukab, O.M. Unforgeable Digital Signature Integrated into Lightweight Encryption Based on Effective ECDH for Cybersecurity Mechanism in Internet of Things. Processes 2022, 10, 2631. https://doi.org/10.3390/pr10122631
Ahmed AA, Barukab OM. Unforgeable Digital Signature Integrated into Lightweight Encryption Based on Effective ECDH for Cybersecurity Mechanism in Internet of Things. Processes. 2022; 10(12):2631. https://doi.org/10.3390/pr10122631
Chicago/Turabian StyleAhmed, Adel A., and Omar M. Barukab. 2022. "Unforgeable Digital Signature Integrated into Lightweight Encryption Based on Effective ECDH for Cybersecurity Mechanism in Internet of Things" Processes 10, no. 12: 2631. https://doi.org/10.3390/pr10122631
APA StyleAhmed, A. A., & Barukab, O. M. (2022). Unforgeable Digital Signature Integrated into Lightweight Encryption Based on Effective ECDH for Cybersecurity Mechanism in Internet of Things. Processes, 10(12), 2631. https://doi.org/10.3390/pr10122631