1. Introduction
With the complexity and refinement of the process of industrial production, the production process is more and more inseparable from real-time monitoring of the system. An alarm management system, as an indispensable part in the safety operation of industrial production, has been paid more and more attention by all walks of life. In industrial practice, cases with more false alarms, a higher false alarm rate (FAR) and a missed alarm rate (MAR) always arise in processes [
1], which are mainly caused through the unreasonable threshold settings for variables and ineffective management for alarm systems. Based on the studies from EEMUA, the range of alarm numbers that an operator could effectively handle for one alarm is from every 5 min to 10 min [
2].
Regarding the methods of alarm optimization, academia has given many methods, each of which plays a certain role in its corresponding system to a greater or lesser extent. There are many kinds of alarm optimization methods, and classification methods are inconclusive. Generally speaking, they can be divided into univariate methods and multivariate methods, threshold optimization methods and algorithm optimization methods, off-line methods and dynamic methods, etc.
For determining the process variable threshold, academia has studied many optimization methods. For instance, in terms of FAR and MAR, an approach for estimating the threshold was proposed on account of an adaptive fuzzy-neural network and genetic learning algorithm [
3]. As the threshold can be determined by the deadband, a method with the objective function about FAR and MAR, and the relation between the optimal threshold and deadband to estimate the threshold, was presented [
4]. Combining FAR and MAR with a correlation coefficient, an off-line method for optimizing thresholds was given to reduce alarms for multi-variables based on time delay [
5]. For improving the robustness classification performance in the system with regard to separation threshold selection, different intelligent pattern classifiers were used to mine industrial batch dryer data to determine thresholds [
6]. In addition, there also have many methods in setting thresholds in early warning and damage systems [
7,
8], alarms reduction [
9], systems monitoring [
10,
11], and performance optimization [
6,
12].
Over the past five years, based on intelligent algorithms, some similar methods have been improved. For instance, to remove chattering alarms, a univariate method was presented for addressing the reduction of alarms with median filters [
13]. Taking the missed alarms and false alarms into account, an off-line univariate approach for determining alarm threshold in debris flow forecasting was presented, with the lowest missed-alarm and false-alarm probabilities [
14]. By optimizing positioning accuracy, the pulse-width multiplexing Φ-OTDR and multisensor information fusion algorithm were utilized to reduce the nuisance alarm rate [
15]. For target tracking in a chaotic environment, a mul-tivariate approach was proposed to optimize the joint threshold and power allocation strategy with a two-variable nonconvex optimization problem for the cognitive radar network, containing the detection stage and transmitting stage [
16]. Based on the test observations, an off-line simple and robust approach was proposed to determine the detection thresholds for detecting defluidization in the early stage [
17]. Some approaches about optimal alarm identification [
18], design and evaluation analysis for an alarm system [
19,
20,
21,
22,
23], management framework [
24], alarm threshold [
25], and an overview of industrial alarm systems [
26] also have appeared. Variables in most of the above approaches have not been clustered with optimized thresholds, which could be suitable for analyzing interlinks among similar variables. Therefore, Zhang et al. presented an off-line multivariate method based on ROC curve and sensitivity, considering the sensitivity relationship and clustering analysis among variables, to optimize the alarm threshold [
27]. A multivariate alarm clustering method was proposed that takes advantage of the information contained in the alarm logs themselves, of which the clustering analysis for process alarms was achieved through word embedding [
28]. Analyzing alarm data, Lucke et al. presented an on-line method that conducted a practical application for alarm flood classification based on a set of historical alarm floods [
29]. In the process, for high-dimension variables, the number of alarms needing addressing increases significantly when the number of measurable variables increases. False alarms caused by redundant disturbances will disturb operators, leading to alarms having more significance on the system being missed as a consequence. Thus, clustering variables into groups is necessary for alarm optimization.
Most of the above alarm optimization methods are based on the off-line system optimization, and the results obtained in the corresponding systems are also obvious, large or small, effectively optimizing the production process and reducing losses. Thus, to promptly detect the chattering alarms and effectively reduce the number of chattering alarms, an on-line method was given to detect alarms in a timely manner [
30]. As for the HVAC systems, Chakraborty et al. put forward a novel dynamic threshold method with a data-driven model using extreme gradient boosting (XGBoost), which mainly utilized early fault detection [
31]. The static and dynamical performance analyses were used to update evidence in designing the industrial alarm system to reduce unnecessary alarms [
32]. There are also some corresponding approaches for optimization, such as alarm management strategy [
33], alarming mechanism [
34], and threshold setting [
35], which have promoted the development of dynamic methods to a certain extent.
However, as the current industrial production processes change irregularly, the preceding production process and the following process cannot be consistent all the time, such as the changes caused by different conditions or an abnormal process. In view of the problem, a new alarm threshold optimization method is proposed, which uses the correlation degrees among the variables and clustering analysis. Herein, this paper mainly has four significant contributions. (1) It considers the gray correlation degree analysis. Variables with similar influence on the system can be found out through correlation analysis. (2) It could carry on the group sorting according to the intrinsic clustering analysis. (3) It reduces FAR and also has a significant inhibitory effect on MAR (significantly reduced invalid alarms). (4) It can be used as a reference for real-time online optimization. When connecting the current programs to the computer interface in on-line systems, it could meet the requirements of the fast-changing production processes through setting an update period and data, which would consider the alarm rates. In addition, this method could help operators reduce operation load, make more efficient repair measures in a timely manner, and reduce the losses.
2. Optimum Design Outline
2.1. Alarm Efficiency Index
At present, an alarm system is important for safety, which generally utilizes FAR and MAR as efficiency indices to measure the accuracy of detecting operation conditions [
36]. Based on the operation conditions, industrial processes usually contain normal and abnormal situations, which generally use the FAR and MAR to represent the probability directly for a variable when its measured values go beyond the threshold in normal operations, and within the threshold in abnormal operations in an alarm system [
37].
The FAR and MAR can be obtained as follows:
Initially, for a variable x, within a period of time, two groups of data under normal and abnormal situations are obtained. Where a group of data are collected as the normal data when the process runs normally and steadily, another set of data are collected as the abnormal data when the process deviates from normal operation state obviously, which contains added disturbance or failure.
Later, for a variable x, the probability density functions
f(
x) and
g(
x) under the two situations, respectively, are obtained by fitting the corresponding data, which can be shown in
Figure 1, where
xT denotes as the alarm threshold. For a certain parameter of the system,
xT indicates that the parameter has a well running state under the current threshold. When it exceeds or falls below the current threshold, the process may generate redundant false alarms or missed alarms. Here, false alarms will be activated when normal process variable values (the blue line) falls below
xT, and missed alarms will be activated when the abnormal process variable values (red dotted line) exceed
xT.
Finally, given the
, based on
Figure 1 and the Equations (1) and (2) [
5,
36], the FAR and MAR can be obtained.
The following work in this paper can be conducted when the functions (f(x) and g(x)) for a variable can be fitted which was irrelevant to the distribution.
2.2. Alarm Clustering Analysis
Based on the alarm clustering algorithm, variables can be clustered into groups.
A measure of the degree of correlation between two factors in a system that varies from time to time or from object to object is called the correlation degree [
38]. In a system process, if the trend of change of the two factors is consistent, that is, the degree of synchronous change is high, then the degree of correlation is high. Conversely, it is lower. Thus, the gray correlation analysis method is a method to measure the correlation degree among factors according to the degree of similarity or difference of development trend among factors, that is, “gray correlation degree”.
Specific calculation steps for correlation analysis:
- (1)
Determine the reference sequence and comparison sequence. The data sequence that reflects the behavior characteristics of a system is called a reference sequence and the data sequence composed of factors that affect the behavior of a system is called a comparison sequence;
- (2)
Conduct dimensionless treatment for the reference sequence and comparison sequence.
Due to the different physical meanings of each factor in the system, the dimensionality of the data may not be the same, which is not convenient for comparison, or it is difficult to get the correct conclusion when comparing. Therefore, in the analysis of gray relational degree, dimensionless data processing should be generally required.
- (3)
Determine the reference sequence and comparison sequence of the gray correlation coefficient ξ(Xi).
The correlation degree is essentially the difference in geometry among curves. So, the difference among curves can be used as a measure of the correlation degree. For a reference sequence
, there are several comparison sequences
X1,
X2, …,
Xm, the correlation coefficient ξ
i(
k) of each reference sequence and comparison sequence each time is deduced by the following formula:
where,
P is the distinguish coefficient, the value range of which is generally between 0–1, with 0.5 as the common value;
represents the absolute difference between the sequences
Xi and
X0 at point
k;
l = 1, 2, …,
n,
is the minimum difference of the first level, which represents the minimum difference between sequences
Xj(
l) and
X0(
l) at each point;
is the minimum difference of the second level, which represents the minimum difference in all sequences based on the minimum difference found in each sequence;
is the maximum difference of the first level, which represents the maximum difference between sequences
Xj(
l) and
X0(
l) at each point;
is the maximum difference of the second level, which represents the maximum difference in all sequences based on the maximum difference found in each sequence.
In order to avoid the resulting deviation caused by variable units and other factors, it is necessary to conduct standardized processing on variable data.
- (4)
Calculate the correlation degree
As the correlation coefficient denotes the value of correlation degree between the comparison sequence and the reference sequence at each time, it has more than one value, which could lead the information to be too scattered to facilitate the overall comparison. Therefore, it is necessary to concentrate the correlation coefficient of each moment into a value, that is, to find its average value, as the value expression of the correlation degree between the comparison sequence and the reference sequence.
Correlation degree
ri represents the gray correlation degree of comparison sequence
Xi to reference sequence
X0, also called sequence correlation degree, average correlation degree, and line correlation degree, the formula of which is shown as follows:
The closer the value of ri is to 1, the better the correlation is.
- 2.
Clustering analysis
Specific clustering steps:
- (1)
Calculate the gray correlation coefficients between every two variables, then sum the distances;
- (2)
Calculate the correlation degree standard deviations of the above sums, utilizing wd to denote the deviation result;
- (3)
Based on the relationship between
wd (the value obtained by 0–1 normalization for the summation of the correlation coefficients of one variable to all other variables) and
Cg (global correlation degree level), and the relation of Pearson correlation coefficients and correlation levels [
39], variables are clustered into groups, listed in
Table 1. Then, the variable weight of a variable in one group can be calculated through the data of variables in the group.
- 3.
Variable weight calculation
The variable weight of a variable in one group can be determined through the mean square error method with specific steps, as below:
- (1)
Data normalization
where,
denotes the initial data of the
jth variable in group
i.
- (2)
- (3)
- (4)
Herein, two efficiency indices are introduced totally, FAR and MAR. Compared with MAR, the correlation degree mainly reflects on FAR, which has a significant effect on the system. Therefore, the weight
wij is given for FAR. Meanwhile,
MAR/
RMAR is used in case of overlarge MAR, where
RMAR denotes the maximum acceptable MAR, values of which generally less than the engineering required error (0.05) with 0.01, recommended by [
2].
2.3. Threshold Optimization
The optimization objective function, shown as Equation (9), is established according to the alarm information under normal and abnormal situations, which is solved by the numerical optimization method from the point of view of minimizing.
where,
denotes the maximum acceptable FAR, the value of which generally less than the engineering required error (0.05) with 0.01, recommended by [
2].
Figure 2 depicts the flow chart of a quadratic interpolation optimization algorithm with the basic thought shown as: for
F(
x) = Min
φ(
x) (
x∈
R1), the
φ(
x) can be fitted by
y(
x), which consists of some dots. Then, the extreme point
μ of
y(
x) is an estimate value of
x*.
A threshold optimization algorithm is implemented as follows:
- (1)
Give the initial interval [x1,x3], three points (x1, y1), (x2, y2), (x3, y3), and convergence precision ε, where, x1 < x2 < x3, ε > 0;
- (2)
Calculate c1, c2 (where, c1 = (y3 − y1)/(x3 − x1), c2 = [(y2 − y1)/(x2 − x1) − c1]/(x2 − x3)), and xp = 0.5(x1 + x3 − c1/c2), yp = f(xp);
- (3)
If |y2 − yp| ≥ ε, then go step (4), otherwise, go step (9);
- (4)
If xp > x2, then go step (5), otherwise, go step (7);
- (5)
If y2 ≥ yp, then x3 = xp, y3 = yp, return to step (2) otherwise, go step (6);
- (6)
Let x1 = x2, y1 = y2, x2 = xp, y2 = yp, return to step (2);
- (7)
If y2 < yp, then x1 = xp, y1 = yp, return to step (2) otherwise, go step (8);
- (8)
Let x3 = x2, y3 = y2, x2 = xp, y2 = yp, return to step (2);
- (9)
If y2 < yp, then x* = x2, y* = y2, otherwise, go step (10);
- (10)
x* = xp, y* = yp;
- (11)
Output x* = xp, f* = f (x*).
2.4. Optimization Process Description
Figure 3 gives the optimization algorithm, the specific explanations of which are shown as follows:
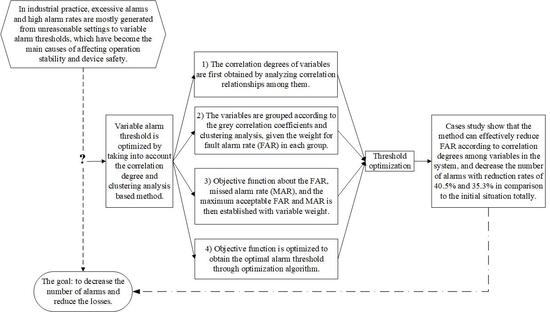
To begin with, the correlation degrees of variables are obtained by analyzing correlation relationships among them. Subsequently, the variables are grouped according to the gray correlation coefficients and clustering analysis, given the weight ωi for FAR in each group. An objective function about the FAR, MAR, RFAR, RMAR, and ωi is then established with variable weight. Eventually, based on the optimization algorithm, the objective function is optimized for obtaining the optimal alarm threshold.
5. Conclusions
In this work, correlation degree and clustering analysis based method is presented to achieve threshold optimization: the gray correlation coefficients of variables are first obtained by analyzing correlation degrees among them; the variables are grouped later according to the correlation degree and clustering analysis, given the weight ωij for FAR in each group; optimization algorithm is finally utilized to optimize objective function about FAR, MAR, RFAR, RMAR, and ωij to complete threshold optimization.
According to the analysis of case theory study with TE simulation process and actual industrial verification for industrial ethylene production process, the results manifest the presented approach can not only reduce FAR, have significant inhibitory effect on MAR, and decrease the number of alarms effectively in total, but could carry on the grouping sorting according to the intrinsic clustering analysis, which could help operators reduce operation load. Meanwhile, it will also leave operators more time to make more efficient repair measures timely and reduce losses through helping them to identify variables that have larger and more rapid impact on system, extend the deteriorative time for abnormity.