Comparison of Knudsen Diffusion and the Dusty Gas Approach for the Modeling of the Freeze-Drying Process of Bulk Food Products
Abstract
:1. Introduction
2. Methodology
2.1. Model Structure
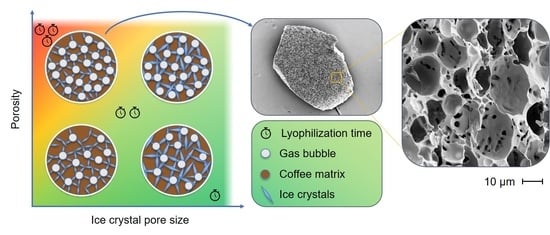
- Only the vapor transport within the porous structure of the particle is investigated, while the vapor transport within the drying chamber is neglected.
- The material is homogeneously distributed within each respective model region.
- The pores all have the same pore diameter and are connected to the outside of the particle. Closed pores are neglected.
- Material properties are independent of the temperature.
- Particles have a spherical shape.
- The influence of the sample holder is neglected and only radiative heat transfer is considered.
- Only radiative heat transfer in the drying chamber is considered. The particle is modeled as a gray body.
2.2. Validation Experiments
3. Results
3.1. Experimental Results
3.2. Model Results
3.2.1. Validation
3.2.2. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| OR | Overrun |
| PSD | Particle size distribution |
| SEM | Scanning electron microscopy |
| SSHE | Scarped surface heat exchanger |
References
- Khalloufi, S.; Robert, J.L.; Ratti, C. Solid foods freeze-drying simulation and experimental data. J. Food Process Eng. 2005, 28, 107–132. [Google Scholar] [CrossRef]
- Ratti, C. Hot air and freeze-drying of high-value foods: A review. J. Food Eng. 2001, 49, 311–319. [Google Scholar] [CrossRef]
- Hottot, A.; Vessot, S.; Andrieu, J. A Direct Characterization Method of the Ice Morphology. Relationship Between Mean Crystals Size and Primary Drying Times of Freeze-Drying Processes. Dry. Technol. 2004, 22, 2009–2021. [Google Scholar] [CrossRef]
- Pikal, M.J.; Cardon, S.; Bhugra, C.; Jameel, F.; Rambhatla, S.; Mascarenhas, W.J.; Akay, H.U. The nonsteady state modeling of freeze drying: In-process product temperature and moisture content mapping and pharmaceutical product quality applications. Pharm. Dev. Technol. 2005, 10, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Liapis, A.I.; Bruttini, R. A mathematical model for the spray freeze drying process: The drying of frozen particles in trays and in vials on trays. Int. J. Heat Mass Transf. 2009, 52, 100–111. [Google Scholar] [CrossRef]
- Sebasti ao, I.B.; Bhatnagar, B.; Tchessalov, S.; Ohtake, S.; Plitzko, M.; Luy, B.; Alexeenko, A. Bulk Dynamic Spray Freeze-Drying Part 1: Modeling of Droplet Cooling and Phase Change. J. Pharm. Sci. 2019, 108, 2063–2074. [Google Scholar] [CrossRef]
- Song, C.S.; Yeom, G.S. Experiment and numerical simulation of heat and mass transfer during a spray freeze-drying process of ovalbumin in a tray. Heat Mass Transf. 2009, 46, 39–51. [Google Scholar] [CrossRef]
- Sadikoglu, H.; Liapis, A.I. Mathematical Modelling of the Primary and Secondary Drying Stages of Bulk Solution Freeze-Drying in Trays: Parameter Estimation and Model Discrimination by Comparison of Theoretical Results with Experimental Data. Dry. Technol. 1997, 15, 791–810. [Google Scholar] [CrossRef]
- Sheehan, P.; Liapis, A.I. Modeling of the primary and secondary drying stages of the freeze drying of pharmaceutical products in vials: Numerical results obtained from the solution of a dynamic and spatially multi-dimensional lyophilization model for different operational policies. Biotechnol. Bioeng. 1998, 60, 712–728. [Google Scholar] [CrossRef]
- Liapis, A.I.; Bruttini, R. Fundamentals of modeling and analysis of spray freeze drying: The drying of frozen pharmaceutical and food particles in packed beds. In Proceedings of the 17th International Drying Symposium, Magdeburg, Germany, 3–6 October 2010; pp. 71–80. [Google Scholar]
- Her, J.Y.; Song, C.S.; Lee, S.J.; Lee, K.G. Preparation of kanamycin powder by an optimized spray freeze-drying method. Powder Technol. 2010, 199, 159–164. [Google Scholar] [CrossRef]
- Warning, A.D.; Arquiza, J.; Datta, A.K. A multiphase porous medium transport model with distributed sublimation front to simulate vacuum freeze drying. Food Bioprod. Process. 2015, 94, 637–648. [Google Scholar] [CrossRef]
- Gruber, S.; Vorhauer-Huget, N.; Foerst, P. In situ micro-computed tomography to study microstructure and sublimation front during freeze-drying. Food Struct. 2021, 29, 100213. [Google Scholar] [CrossRef]
- Vorhauer-Huget, N.; Mannes, D.; Hilmer, M.; Gruber, S.; Strobl, M.; Tsotsas, E.; Foerst, P. Freeze-Drying with Structured Sublimation Fronts—Visualization with Neutron Imaging. Processes 2020, 8, 1091. [Google Scholar] [CrossRef]
- Vorhauer, N.; Först, P.; Schuchmann, H.; Tsotsas, E. Pore network model of primary freeze drying. In Proceedings of the 21th International Drying Symposium, Valencia, Spain, 11–14 September 2018. [Google Scholar] [CrossRef] [Green Version]
- Searles, J.A.; Carpenter, J.F.; Randolph, T.W. The ice nucleation temperature determines the primary drying rate of lyophilization for samples frozen on a temperature–controlled shelf. J. Pharm. Sci. 2001, 90, 860–871. [Google Scholar] [CrossRef] [PubMed]
- Kast, W.; Hohenthanner, C.R. Mass transfer within the gas-phase of porous media. Int. J. Heat Mass Transf. 2000, 43, 807–823. [Google Scholar] [CrossRef]
- Jackson, R. Transport in porous catalysts. In Chemical Engineering Monographs; Elsevier: Amsterdam, The Netherlands, 1977; Volume 4. [Google Scholar]
- Mason, E.A.; Malinauskas, A.P.; Malinauskas, A.P. Gas transport in porous media: The dusty-gas model. In Chemical Engineering Monographs; Elsevier: Amsterdam, The Netherlands, 1983; Volume 17. [Google Scholar]
- Gloor, P.J.; Crosser, O.K.; Liapis, A.I. Dusty-gas parameters of activated carbon absorbent particles. Chem. Eng. Commun. 1987, 59, 95–105. [Google Scholar] [CrossRef]
- Marti, J.; Mauersberger, K. A survey and new measurements of ice vapor pressure at temperatures between 170 and 250 K. Geophys. Res. Lett. 1993, 20, 363–366. [Google Scholar] [CrossRef]
- Levin, P.; Meunier, V.; Kessler, U.; Heinrich, S. Influence of Freezing Parameters on the Formation of Internal Porous Structure and Its Impact on Freeze-Drying Kinetics. Processes 2021, 9, 1273. [Google Scholar] [CrossRef]
- Wegiel, L.A.; Ferris, S.J.; Nail, S.L. Experimental Aspects of Measuring the Vial Heat Transfer Coefficient in Pharmaceutical Freeze-Drying. AAPS PharmSciTech 2018, 19, 1810–1817. [Google Scholar] [CrossRef] [PubMed]
- Rambhatla, S.; Pikal, M.J. Heat and mass transfer scale-up issues during freeze-drying, I: Atypical radiation and the edge vial effect. AAPS PharmSciTech 2003, 4, E14. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Step | T | T | P | t |
|---|---|---|---|---|
| (C) | (C) | (mbar) | (min) | |
| 1 | −30 | −30 | 1013 | 1 |
| 2 | −30 | 46 | 0.4 | 38 |
| 3 | 46 | 46 | 0.4 | 90 |
| 4 | 46 | 25 | 0.4 | 20 |
| (mm) | (µm) | ( - ) | (min) | (kg/h) |
|---|---|---|---|---|
| 2.65 | 2.88 | 0.743 | 44.4 ± 2.2 | 2.36 ± 0.20 |
| 2.67 | 7.20 | 0.771 | 39.4 ± 0.1 | 3.03 ± 0.00 |
| 2.84 | 9.49 | 0.759 | 39.1 ± 0.5 | 3.05 ± 0.04 |
| 2.60 | 5.34 | 0.692 | 44.4 ± 1.2 | 3.56 ± 0.10 |
| 2.50 | 7.71 | 0.796 | 37.4 ± 1.6 | 2.47 ± 0.11 |
| (mm) | (µm) | ( - ) | ( - ) | ( - ) |
|---|---|---|---|---|
| 2.65 | 2.88 | 0.743 | 0.995649 | 0.995648 |
| 2.67 | 7.20 | 0.771 | 0.995247 | 0.995255 |
| 2.84 | 9.49 | 0.759 | 0.996340 | 0.996339 |
| 2.60 | 5.34 | 0.692 | 0.996624 | 0.996621 |
| 2.50 | 7.71 | 0.796 | 0.994986 | 0.994981 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levin, P.; Buchholz, M.; Meunier, V.; Kessler, U.; Palzer, S.; Heinrich, S. Comparison of Knudsen Diffusion and the Dusty Gas Approach for the Modeling of the Freeze-Drying Process of Bulk Food Products. Processes 2022, 10, 548. https://doi.org/10.3390/pr10030548
Levin P, Buchholz M, Meunier V, Kessler U, Palzer S, Heinrich S. Comparison of Knudsen Diffusion and the Dusty Gas Approach for the Modeling of the Freeze-Drying Process of Bulk Food Products. Processes. 2022; 10(3):548. https://doi.org/10.3390/pr10030548
Chicago/Turabian StyleLevin, Patrick, Moritz Buchholz, Vincent Meunier, Ulrich Kessler, Stefan Palzer, and Stefan Heinrich. 2022. "Comparison of Knudsen Diffusion and the Dusty Gas Approach for the Modeling of the Freeze-Drying Process of Bulk Food Products" Processes 10, no. 3: 548. https://doi.org/10.3390/pr10030548
APA StyleLevin, P., Buchholz, M., Meunier, V., Kessler, U., Palzer, S., & Heinrich, S. (2022). Comparison of Knudsen Diffusion and the Dusty Gas Approach for the Modeling of the Freeze-Drying Process of Bulk Food Products. Processes, 10(3), 548. https://doi.org/10.3390/pr10030548