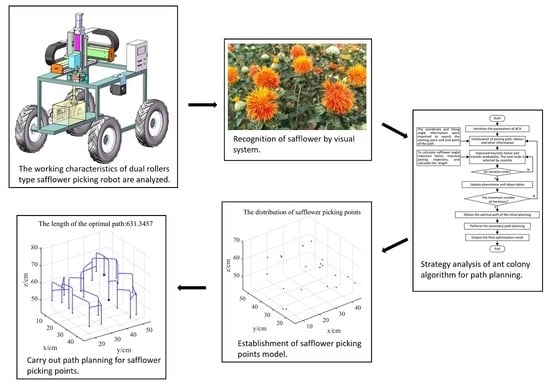
1. Introduction
Safflower combines pharmacology, dyes and oils, and has high economic value [
1]. Safflower plants are spatially distributed, one branch grows one bulb, and the ripening time is different, so safflower needs to be harvested selectively [
2]. Considering that the safflower picking robot picks safflower filaments in the field, the energy consumption should be reduced as much as possible. Due to the short flowering period of safflower, the filaments become dry and hard after the sixth day of safflower opening, which affects the effect of picking safflower filaments by the dual rollers type end-effector. In order to reduce the energy consumption of safflower picking robots and ensure the high net picking rate and low dropping rate of safflower filaments, the working efficiency of safflower picking robots should be improved as much as possible. Therefore, the planned picking path should avoid the end-effector repeatedly passing through the same picking point and wasting more unnecessary energy. It is required to finish picking the whole safflower bulbs with the shortest path length and picking time to improve the working efficiency of the safflower picking robot. Therefore, the path planning of the safflower picking robot is a travelling salesman problem (TSP). In conclusion, in order to improve the picking efficiency of the dual rollers type safflower picking robot, this paper explores a picking path planning method suitable for the dual rollers type safflower picking robot with the overall goal of minimum time and shortest distance.
In order to improve the working efficiency of the robot, two methods are usually used to optimize work paths: One is to optimize work paths by sequencing them with a certain algorithm, that is, for a certain work goal or multiple goals of the robot, the work points are sequenced according to certain evaluation criteria to arrive at the optimal operation sequence. The other is to optimize the motion track, that is, for specified work, the robot end-effector adopts a specific motion track curve from one working point to another, so that the end-effector path runs smoothly [
3].
Among many path planning algorithms for sequences, the ACA [
4] uses a positive feedback mechanism with good collaboration, robustness and strong global search capability [
5], which makes it more widely used in TSP path planning problems [
6,
7,
8]. Xiaoming You et al. define a new dynamic search induction operator to improve the quality of the optimized solution for the problems of long operation time and low solution accuracy when the ACA solves the path planning problem of mobile robots in complex environments [
9]. Zhiwen Cong et al. proposed a smoothness constraint in view of the motion limitation of each joint of tomato picking robots’ mechanical arm subject to kinematics and dynamics constraints. The ACA was improved by setting the transfer probability value according to the smoothness requirement to obtain a smoother and shorter distance picking path for the picking gripper [
10]. Baoji Liu et al. proposed a pheromone update method and state transfer probability function improvement method based on the maximum minimum ACA in order to realize selective and efficient cocoon picking by a cocoon picking machine. This method plans a smoother cocoon picking path, which makes the cocoon picking more efficient [
11]. Jidong Yang et al. improved the ACA selection probability according to the component size and grasping process for the grasping path planning problem of robot grasping components [
12].
Research on motion track planning: Xing Xu et al. used horizontal and vertical fold paths between two points instead of straight paths in the ACA to optimize the storage picking paths in order to improve the efficiency of picking operations in the storage system [
13]. Shasha Zhang et al., aiming at the trellis kiwifruit planting pattern, calculated the center point through the visual system, and then fitted all kiwifruit into concentric circles. The picking sequence is picked from the outer circle to the inner circle to avoid damage to other kiwifruit caused by the mechanical arm touching [
14]. Yanfang Yuan et al. addressed the problem of easy collision between two manipulators in the process of tea picking, partitioned the picking area and then constrained the manipulator movement path to “M” type, which has a better planning effect [
15]. For tea picking, Hualin Yang designed a movement track of the manipulator shaped like ∩ to avoid obstacles and damage to other branches [
16].
From the above, it can be seen that the application of ACA can solve certain path planning problems for mobile robots, picking robots, grasping robots, etc. However, the traditional ACA solves the TSP problem by considering the targets to be selected as coordinate points, ignoring the influence of the target pose on the path planning. Moreover, safflower is a top crop and the safflower bulbs are spatially distributed in a coronal pattern with a large height difference. Existing studies have less research on picking path planning for topiary crops distributed in a certain range of heights.
This paper firstly analyzes the characteristics and requirements of safflower picking for dual rollers type end-effector, and then proposes a safflower picking path planning strategy. This paper innovatively proposes to improve the pheromone heuristic factor by using safflower inclination difference and distance as a two-factor, which solves the limitation of traditional ACA that only uses distance as the node selection factor and enhances the path selection directionality. Combined with the feature that safflower is a top crop, the specific spatial picking track is designed and the track length is used as the distance factor of the ACA, which breaks the traditional ACA using the straight-line distance between two points as the distance factor, and this innovation makes the calculation of the picking path length more accurate. The effectiveness of the angle-inducing factor, picking track optimization and secondary path optimization were verified by three single-factor comparative simulation experiments, respectively. Finally, the comprehensive simulation experiments verified the effectiveness of the improved ACA for path planning.
2. Analysis on the Picking Path of Dual Rollers Type Safflower Picking Robot
2.1. Working Principle of Dual Rollers Type Safflower Picking Robot
Dual rollers type safflower picking robot [
17] is mainly composed of the dual rollers type end-effector, three-axis linear manipulator, visual identification system, control box, etc. The end-effector is connected to the three-axis linear manipulator, and the movement of the three-axis linear manipulator can drive the end-effector to work in a certain range of space. Overall structure is shown in
Figure 1. The robot uses a plant-by-plant harvesting method, and stops when it moves over a safflower. Firstly, three-dimensional coordinate information and tilting angle information of the safflower picking points were obtained by visual system. Then the controller drives the end-effector to move to the picking point according to the specified picking track according to the obtained coordinate information. The controller then drives the end-effector by the steering engine to rotate the corresponding angle according to the safflower tilting information, and then starts the motor in the end-effector for filaments picking. After picking a bulb, the controller then drives the end-effector along the specified picking track to the next picking point according to the sequence of picking points planned by the algorithm. When the whole safflower bulbs are picked, the walking device moves along the rows of safflower plants and circulates the above working process to pick the next safflower [
2].
When the dual rollers type end-effector works, the motor inside the picking device drives the rollers to rotate at high speed towards each other, which will form an airflow to bring the filament clusters together. When the filaments touch the surface of the rubber rollers, a frictional force F is generated, which is in the same direction as the linear velocity of the rubber rollers and perpendicular to the centripetal force. When the friction angle is greater than the feeding angle α, the filaments can be separated from the bulb under the action of rollers pressure and friction [
18]. The principle diagram of dual rollers picking safflower is shown in
Figure 2a. However, when the safflower bulb is tilted, if the angle of the rollers is not adjusted accordingly, part of the filaments can not be involved in the gap between the dual rollers, which will affect the filaments picking rate. Therefore, in order to obtain better safflower picking effectiveness, it is necessary to rotate the angle of the end-effector correspondingly according to the safflower tilting angle.
Figure 2b shows the effectiveness of picking tilted safflower with the dual rollers end effector.
2.2. Safflower Picking Path Planning Strategy Analysis
Due to the unique spatial growth characteristics of safflower plants and the working characteristics of the dual rollers type end-effector, the main factors affecting the safflower harvesting effectiveness include the tilting angle of safflower, the distance between safflower and the rollers, and the distance between bulbs. In this paper, considering the influence of various factors, the optimal safflower picking sequence was obtained by sorting safflower picking points according to certain evaluation criteria. This study mainly uses the following strategies to carry out path planning for safflower picking points:
(1) Firstly, the safflower tilting angle induction factor was introduced to constrain the transition probability. When picking a safflower bulb, the next picking point comprehensively considers the bulb with a small difference in tilting angle and a short distance from the current picking point. The smoothness of the tilting angle between picking points can ensure that the end-effector can reduce unnecessary angle rotation during the moving process, so that the end-effector can run smoothly and reduce the waiting time.
(2) Secondly, the ∩-shaped picking track was used as the picking track between bulbs to reduce the shock of safflower branches caused by the end-effector hitting bulbs during the picking process. Moreover, by optimizing the ∩-shaped picking track, the length of the picking path is greatly shortened.
(3) At last, this paper carried on the secondary path optimization to the initial optimal path. Thresholds with reference to the roll length and bulbs diameter were set. The two picking points within the threshold were combined into one point for simultaneous picking, which can reduce the number of picking points and improve the efficiency of safflower picking.
3. Improved Ant Colony Algorithm
According to the different working requirements of robots, the requirements of path planning such as path safety, smoothness, shortest distance and least time are put forward [
19,
20,
21]. In view of the picking path planning of the dual rollers type safflower picking robot, with the goal of realizing the efficient operation of the robot, this paper takes the picking time and path length as the comprehensive evaluation indicators, improves the traditional ACA and applies it to the planning of the safflower picking path.
3.1. Design Angle Induction Factor and Time Evaluation Function
The traditional ACA takes the shortest path as the single planning objective, and the pheromone heuristic value is only determined by the distance. In this section, the angle inducing factor is introduced, and the pheromone heuristic factor is improved by using distance factor and angle induction factor. The ACA comprehensively considers the picking points with shorter path length and smaller angle difference when selecting the next picking point, instead of simply selecting the next picking point with the closest distance or the smallest angle. In order to verify the effectiveness of the angle induction factor algorithm, the picking time was used as the evaluation index.
3.1.1. Angle Inducing Factor
The growth morphology of safflower is shown in
Figure 3. Members of the project team measured the plants in the field on 10 July 2021. The maximum bulb diameter was 3.24 cm, the average bulb diameter was 2.76 cm, the maximum height difference between adjacent bulbs was 6.8 cm, the average difference between the highest and lowest bulbs was 27.9 cm and the maximum tilting angle of the outer bulb was about 45° [
22].
In order to obtain better harvest effectiveness of safflower, the end-effector should be rotated accordingly when the safflower bulb is tilted. Therefore, when selecting the next picking point, the ACA not only considers the distance between the two picking points, but also considers the tilting angle difference between the next alternative picking point and the current picking point to reduce unnecessary angle rotation. The safflower tilting angle refers to the angle between the vertical line and the safflower prediction frame obtained by the image processing technology. If the safflower prediction frame is in the clockwise direction of the vertical line of the bulb centroid, the tilting angle is positive, otherwise it is negative, as shown in
Figure 4. When the difference between the tilting angles of the two picking points is positive, the end-effector needs to rotate counterclockwise, otherwise, the end-effector needs to rotate clockwise.
The pheromone heuristic factor of the traditional ACA is:
In this paper, the angle induction factor is introduced to improve the pheromone heuristic factor to guide ants to search. The smaller the tilting angle difference, the greater the probability of being selected. Because the maximum tilting angle of the outermost bulbs does not exceed 45° [
22], the maximum tilting angle difference between any two bulbs is no more than 90°, so the cosine function is used as the angle factor in this paper. The angle inducing factor can be described as:
where
φi and
φj are the tilting angles of picking points i and j respectively.
φij is the angle inducing factor between the two points, which represents the influence coefficient of the safflower tilting angle difference on the transition probability, and its value is a positive value. The positive or negative of the tilting angle difference between the two picking points only affects the rotation direction of the end-effector, and does not affect the positive or negative of the angle inducing factor. When the difference between the tilting angles of the two bulbs is 0°, the end-effector does not need to rotate, and the corresponding cosine value reaches the maximum value 1, that is, the angle inducing factor reaches the maximum value 1. As the angle difference increases, the end-effector needs to rotate the corresponding angle, and the angle inducing factor value decreases.
The pheromone heuristic factor formula is updated as:
In this paper, the ratio of the angle inducing factor to the distance factor is used to improve the pheromone heuristic factor. The larger the angle inducing factor and the smaller the distance factor, the greater the probability of being selected. With the change of the angle inducing factor and the distance factor, the pheromone heuristic factor value is dynamically adjusted. The angle induction factor only affects the probability of bulb selection, not the decisive factor of whether the bulb is picked preferentially.
3.1.2. Time Evaluation Function
Because the angle rotation of the end-effector takes a certain amount of time, when the angle is changed too much, the total picking time will be too long. In order to verify the effectiveness of the angle induction factor algorithm proposed in this paper, the picking time
T was used as the evaluation index. Because under the condition of the same speed, the greater the rotation angle of the steering engine and the longer the time required; the time is proportional to the rotation angle. So let the waiting time function generated by angle rotation of the end-effector be:
where
T is the rotation time of the end-effector and its unit is s.
φi and
φj are the inclination angles of the bulbs, and the unit is °.
K is the time constant, which is determined by the performance of the steering engine, and the unit is s/°.
The speed of the steering engine will affect the angle rotation time of the end-effector. The speed of the steering engine is measured by the time it takes for the steering engine to turn a 60° angle without load; the speed of the common steering engine is generally between 0.11 s/60° and 0.21 s/60°. In this paper, the speed of the steering engine at 0.18 s/60° is used, so it takes 0.003 s for the steering engine to turn 1°. Therefore, the evaluation function of waiting time generated by the angle rotation of the end-effector is:
3.2. Picking Track Optimization
For the movement process of safflower picking robots, not only the sequence of picking points should be planned, but also the movement track of the end-effector between any two picking points should be defined according to the working environment and task requirements. In this section, under the condition that the ACA has planned the sequence of safflower picking points, the movement track between the picking points is studied so that the end-effector can complete the movement from one picking point to another according to the expected track.
3.2.1. Establishment of Picking Track Model
Safflower is a top crop with bulbs on the top of branches. If the safflower is picked by connecting two picking points with a straight line as the picking track, the safflower branches may oscillate during the movement of the end-effector. A single swinging branch may cause other branches to swing, thus affecting the picking effectiveness and reducing the picking efficiency.
Figure 5a shows the effectiveness diagram of straight-line picking tracks. Considering the working characteristics of the dual rollers type end-effector and the growth characteristics of safflower plants, it is necessary to lift the end-effector to a certain height when moving from one bulb to another to avoid the shock caused by the collision between the end-effector and safflower branches during the movement. Therefore, this paper adopts the ∩-shaped track as the picking track, and this can improve the efficiency of safflower picking.
Figure 5b shows the effectiveness diagram of ∩-shaped picking tracks.
3.2.2. Improvement of ∩-Shaped Picking Track
Zhibin Ma uses an ∩-shaped track to pick tea leaves, and according to the characteristic that the initial working zero point of Delta robot is in the center of the workspace, a three-dimensional world coordinate system is established based on the horizontal plane where the zero point is located. After picking each target point, the end-effector returns to the zero plane and picks the next target point with an ∩-shaped track [
23], which is hereinafter referred to as the fixed plane ∩-shaped track.
However, because the middle safflower bulbs were high and the outer bulbs were low, the height difference between the highest safflower bulbs and the lowest bulbs was 27.9 cm on average, which was significantly different from the height of tea. If the safflower bulbs are still picked on the above track, the useless path would be greatly increased. In order to shorten the picking path, this paper improves on the above ∩-shaped track by setting the ∩-shaped track lifting segment to a fixed height h without returning to the zero plane. That is, the end-effector raises a certain height h after picking a bulb before picking the next bulb.
The comparison of the two picking track models is shown in
Figure 6, in which the blue dotted line is the picking method with the fixed plane ∩-shaped track, and the black solid line is the picking method with the improved ∩-shaped track.
P0 is the initial operating zero point,
P1,
P2,
P3… are safflower picking points. It can be seen from
Figure 6 that the picking method of the improved ∩-shaped track greatly shortened the picking path length compared with the picking method of the fixed plane ∩-shaped track.
In order to solve the problem of ∩-shaped track in the joint coordinate space and rectangular coordinate space during the operation of Delta parallel robot, Xianwei Liu changed the rectangular transition section of the ∩-shaped track to a circular arc as the transition curve, making the whole picking track smoother and reducing the mechanical vibration phenomenon [
24]. This paper refers to the method of circular arc as transition curve.
To sum up, this paper improved the traditional ∩-shaped track, set the lifting section as a fixed height h, adopted the circular arc as the transition curve, which was hereinafter referred to as the fixed height ∩-shaped track, and applied it to safflower picking path planning.
3.2.3. Calculation Method of the Fixed Height ∩-Shaped Track
The three-dimensional coordinates of safflower bulbs are identified and completed by the visual recognition system. Assuming that the spatial coordinates of two safflower bulbs to be picked were
Pi(X
i, Y
i, Z
i) and
Pj(X
j, Y
j, Z
j), the fixed height ∩-shaped track model was established as shown in
Figure 7.
The length of point
Pi to point
A is
h, and points
A’,
B’ and
Pi’ are the symmetric points of points
A,
B and
Pi about the center line MN respectively, so the length of
A’
Pi’ is also
h. Arcs
AB and
A’
B’ are arcs of one quarter radius
r. Since the z-axis coordinates of
Pi and
Pi’ are the same, and the X-axis and Y-axis coordinates of
Pi’ are the same as
Pj, the length between
Pi and
Pi’ is:
Therefore, the expression of track length between any two safflower bulbs to be picked can be obtained:
where the arc length of curve
AB is:
By substituting Equations (8)–(10) into Equation (7), the length between
PiPi+1 is:
Therefore, the distance heuristic factor formula is updated as:
where h and r are the height of the lifting section and the radius of transition section of the fixed height ∩-shaped track, respectively. X
i and Y
i are the abscissa and ordinate of point i. X
j and Y
j are the abscissa and ordinate of point j. The fixed height ∩-shaped track length is used to replace the length of the straight line as the pheromone heuristic factor of the traditional ACA, which makes the calculation of the path length more accurate and the planning effectiveness better.
3.3. Secondary Path Optimization
For the planning of safflower picking path, the number of picking points greatly affects the path length and picking time. If the number of picking points can be reduced, the working efficiency of the robot will be greatly improved. Due to the large difference in the distance between safflower bulbs, the two picking points which were far away from each other were picked with the fixed height ∩-shaped track. However, for the two picking points with a short distance, by optimizing the track, they can be picked at one time using the dual rollers type end-effector. Because the maximum diameter of safflower bulbs is 3.24 cm, taking the length of the rollers is 7 cm as an example, when the distance between the centroid of the two fruit bulbs is within 3.76 cm, theoretically the filaments can be picked. Therefore, the secondary path optimization is carried out on the basis of the initial optimal path, which further shortens the total path length that the end effector works through.
The specific steps of secondary path optimization are to set the threshold value by referring to the length of the dual rollers and the diameter of the safflower bulbs. For the picking points with the distance within the threshold in the initial optimal path, cancel the ∩-shaped picking track between the two picking points, and directly combine the two picking points into one picking point and pick at the same time. The secondary path effectiveness is shown in
Figure 8.
In this paper, when the distance between two picking points is less than or equal to the maximum bulb diameter, the two picking points can be combined into one picking point for simultaneous picking, and the coordinates of the new picking point are the coordinates of the midpoint of the two points. The coordinate adjustment algorithm for short-distance safflower bulbs is as follows: Assuming that the spatial coordinates of the two adjacent safflower bulbs to be picked in the picking sequence are
Pi(X
i, Y
i, Z
i),
Pi+1(X
i+1, Y
i+1, Z
i+1), so the straight-line distance of the two points is:
while
, the new coordinate after secondary path optimization is:
3.4. Algorithm Flow of Improved ACA
The flow chart of picking path planning method of dual rollers type safflower picking robot based on improved ACA is shown in
Figure 9.
The specific steps of the algorithm to search the optimal picking path of safflower are as follows:
(1) Initialize m, G, α, β, ρ and other parameters.
Where m is the number of ants in the ACA, that is, there are m ants searching the path; G is the maximum number of iterations, that is, termination after G iterations; α is the pheromone concentration factor, which reflects the relative importance of pheromone quantity accumulated along the path during ant movement in guiding ant colony search. β is the expected heuristic factor, which reflects the relative importance of heuristic information in guiding ant colony search. ρ is the global pheromone volatilization coefficient, which reflects the disappearance level of pheromone.
(2) Import the spatial coordinate information and tilting angle information of the bulbs obtained from image processing technology. The spatial model of safflower picking was established. Initializing the picking path, taboos table and pheromone concentration, etc.
(3) The safflower tilting angle induction factor was calculated according to bulb tilting angle. The fixed height ∩-shaped track length between two safflower picking points was calculated according to the bulbs sphere coordinate information. Then the improved heuristic factor and transition probability were calculated. The next picking spot is chosen by roulette.
(4) After one iteration is completed, the local pheromone and the global pheromone are updated, and the number of iterations g is increased by 1.
(5) After the number of iterations reaches the maximum value G, output the optimal path information of initial planning.
(6) According to the initial planned bulbs picking sequence, if the length between two adjacent picking points is less than the set threshold parameter, the secondary path optimization is carried out. The two picking points within the threshold were combined into one point for simultaneous picking, and the final optimal path result was output.
4. Simulation Experiment and Analysis
In order to verify the effectiveness of the improved ACA proposed in this paper in the path planning of the safflower picking robot, this paper conducts simulation based on the distribution images of safflower bulbs taken in the field. Four groups of simulation comparison experiments are designed respectively. Experiments 1 to 3 are single-factor comparison experiments of angle induction factor, improved picking track and secondary path optimization. Experiment 4 is a comprehensive verification experiment. By observing the difference in path length and angle rotation time when the end-effector picks the whole safflower, the effectiveness of improved ACA to improve the working efficiency of the safflower picking robot is analyzed. Simulation experiment running environment: Windows 10(64-bit), simulation platform MatlabR2016a. Some parameters in the experiment are shown in
Table 1.
4.1. Validation Experiment of Angle Induction Factor
In order to verify the effectiveness of angle inducing factor to improve pheromone heuristic function, the validity verification experiment of angle inducing factor was carried out. The traditional ACA and the ACA with angle inducing factor were simulated, and the path length, rotation angle and rotation time of the end-effector were taken as evaluation indexes.
Figure 10 shows the simulation results of traditional ACA, and
Figure 11 shows the simulation results of ACA with angle induction factor. In Figure a, the triangular point is the starting point of picking, and the square point is the end point of picking.
From the comparison between
Figure 10 and
Figure 11, it can be seen that the path planned by the ACA with the angle induction factor is not much different from the shortest path length and the response speed of the algorithm planned by the traditional ACA. However, in the picking sequence planned by the ACA with the angle induction factor, the tilting angle difference between the safflower bulbs is much smaller than that of the traditional ACA, and the rotation time of the end-effector is shortened by 0.312 s.
4.2. Comparative Experiment of Improved Picking Track
Considering that the average diameter of safflower bulb is 2.76 cm, the radius
r of the transition arc should be smaller than the radius of safflower bulbs, otherwise, the movement between two bulbs cannot be accomplished with the fixed height ∩-shaped track. Therefore, the radius
r of the transition arc of the two safflower bulbs picking track is set as 1 cm in this paper. Considering that the maximum height difference between adjacent fruit bulbs is 6.8 cm, the end-effector should be slightly higher than the higher safflower bulbs during picking in order to avoid collision with safflower bulbs, so the height h of the rising section of the fixed height ∩-shaped track is set as 10 cm. In the case of the same safflower bulbs distribution, the picking path planning of the fixed plane ∩-shaped track and the fixed height ∩-shaped track was simulated respectively.
Figure 12 shows the simulation results of the fixed plane ∩-shaped track, and
Figure 13 shows the simulation results of the fixed height ∩-shaped track.
It can be seen intuitively from
Figure 12 and
Figure 13 that the total length of the path planned by the fixed plane ∩-shaped track is 1917.7251 cm, and the total length of the path planned by the improved picking track with the fixed height of 10 cm is 631.3457 cm. The total length of the path planned by the fixed plane ∩-shaped track is about three times that of the fixed height ∩-shaped track. The results showed that it was feasible to shorten the picking path of safflower with the fixed height ∩-shaped track.
4.3. Validation Experiment of Secondary Path Optimization
Figure 14 is the optimal safflower picking path result obtained by initial path planning with the fixed height ∩-shaped track.
Figure 15 is the simulation result of secondary path optimization. In the Figure, the triangle point is the starting point of picking, the square point is the end point of picking, and the star point is the merging point.
By comparing
Figure 14 with
Figure 15, it can be seen intuitively that picking points A
1 and A
2 are merged into point A, picking points B
1 and B
2 are merged into point B, and picking points C
1 and C
2 are merged into point C. The number of picking points was reduced by secondary path optimization, and the length of picking path was shortened from 609.2835 cm to 543.0894 cm; the picking path was shortened by 10.8%. The simulation results show that the secondary path optimization can obtain better planning results and increase the flexibility of the end-effector picking point path.
4.4. Comparative Experiment of Improved ACA
In order to verify the effectiveness of the improved ACA for safflower picking path planning, this paper analyzes and researches safflower picking path planning on the basis of fully researching the characteristics of safflower. First, 100 safflower plants with different morphological parameters were selected in this simulation experiment to measure the number of bulbs and the height difference between the highest bulb and the lowest bulb. The selection of test sample plants was carried out according to the provisions of the China agricultural industry standard NY/T1133-2006 [
25]. The field test method is as follows: in the experimental field, the plot is divided into four blocks by connecting the cross line from the midpoint of the long and wide sides of the plot to the midpoint of the opposite side. Two diagonal blocks are randomly selected as detection points. Along the diagonal of the detection plot, 1/4 and 3/4 points from the corner are the detection points, plus the intersection of the two detection plots, a total of five detection points are determined. Selecting 20 plants randomly from each test point, a total of 100 plants were selected. The number of bulbs and the height difference between the highest bulb and the lowest bulb of 100 safflower plants are shown in
Table 2.
Among the safflower plants with the largest number of bulbs, the safflower plant with the largest height difference between the highest bulb and the lowest bulb was selected for simulation experiments. The traditional ACA with the fixed plane ∩-shaped picking track and the improved ACA with integrated reference to angle inducing factor, fixed height ∩-shaped picking track and secondary path optimization were used to simulate this safflower plant, respectively. The results of the path planning using the traditional ACA with the fixed plane ∩-shaped picking track are shown in
Figure 16. The results of the path planning using the improved ACA are shown in
Figure 17. In the Figure, the triangle point is the starting point of picking, the square point is the end point of picking, and the star point is the merging point.
By comparing
Figure 16 and
Figure 17, it can be seen that the total length of the path planned by the traditional ACA with the fixed plane ∩-shaped track is 2242.6886 cm, and the total length of the path planned by the secondary path optimization of improved ACA is 575.9403 cm, and the secondary path optimization reduces three picking points and removes the redundant nodes of the path. The optimal path length planned by improved ACA is about 25.68% of that planned by traditional ACA with the fixed plane ∩-shaped track, and the total path length is shortened by 74.32%. Moreover, the rotation time of end-effector was reduced by 0.957 s in the path planned by improved ACA. The simulation results show that the improved ACA is more suitable for safflower picking path planning, and better planning results can be obtained.
5. Discussion
The heuristic factor is an important component of the ACA. Its function is to use heuristic information to guide the robot to select the optimal path according to specific path requirements, which directly affects the convergence, stability and optimality of the algorithm. The safflower angle induction factor was designed to reduce unnecessary angle transitions of the end-effector. The simulation results of Experiment 1 show that the total path length planned by the ACA with angle induction factor is not much different from that planned by the traditional ACA, but the rotation angle of the dual rollers type end-effector is much smaller, and the corresponding picking time is also shorter. This is because the improved ACA can dynamically adjust the pheromone heuristic function under the dynamic distribution of angle factor and distance factor. The picking sequence is jointly influenced by the distance and the tilting angle between safflower bulbs, which makes the path length and rotation angle both smaller.
When the picking sequence of safflower bulbs is determined, the objective of optimizing the picking track is to shorten the picking path length without affecting the rotation angle of the end-effector. The simulation results of Experiment 2 show that the path length based on the fixed height ∩-shaped track is much shorter than that of the fixed plane ∩-shaped track planning. This is because of the large height difference of safflower bulbs, if the picking of one bulb is completed back to the fixed plane, the picking for lower bulbs will produce a longer picking path, which will greatly increase the picking path length of the whole safflower bulbs.
For the TSP problem of safflower picking, the secondary path optimization refers to the combination of picking points near to each other under the condition that the order and track of picking flower balls are determined. The simulation results of Experiment 3 show that the number of picking points is reduced by the secondary path optimization, and the length and time of the path are reduced.
Experiment 4 was a comprehensive comparison between the traditional ACA with the fixed plan ∩-shaped track and the improved ACA with angle inducing factor, improved picking track and secondary path optimization. Simulation results show that the proposed improved ACA is superior to traditional ACA in terms of path length and time.
In this paper, the traditional ACA is improved and applied to the path planning of safflower picking robot, and good planning results are achieved. However, the lifting segment of picking track is set to a certain value in the algorithm, which belongs to static planning. In the subsequent study, a dynamic picking method of the ∩-shaped track with adaptive lifting section height will be designed according to the actual height difference of adjacent picking points to further shorten the picking path length. Because the ACA has the disadvantages of slow convergence speed, easy to fall into the local optimal solution, and there are many algorithms suitable for path optimization, more effective optimization methods can be adopted to improve the working efficiency of safflower picking robot in the future research work.
6. Conclusions
Aiming at the problem of automatic planning of safflower bulbs picking path during the operation of safflower picking robots, we propose an improved ACA for safflower three-dimensional picking path planning combined with the analysis of safflower material characteristics and the working requirements of dual rollers type end-effector.
The algorithm first calculates the angle induction factor based on the safflower tilting information, and then calculates the fixed height ∩-shaped track length factor based on the coordinate information. The double-induced factor enhances the path selection directionality and plans a safflower picking sequence with smaller path lengths and rotation angles. Then, through secondary path optimization, the closer picking points are combined into one point for simultaneous picking, which further improves the picking path quality.
The safflower plants with the largest number of bulbs were selected from a sample of 100 safflower plants. Then the safflower plant with the largest difference in height between the highest and lowest bulbs was selected from the safflower with the largest number of bulbs for the comprehensive simulation experiment. In this limit, the length of the path planned by the improved ACA is 575.9403 cm, and the rotation time of the end-effector is 1.119 s. Compared with the path planned by the traditional ACA with the fixed plan ∩-shaped track, three safflower picking points are reduced, the total length of the path is shortened by 74.3%, and the angle rotation time of the end-effector is reduced by 0.927 s. The simulation results show that the length and picking time of the path planned by the improved ACA are shorter than those of the traditional ACA. The paths planned by the improved ACA are better, and the method is more suitable for safflower picking path planning. The improved ACA proposed in this paper provides a feasible method for multi-objective path planning of safflower in a practical environment.
Author Contributions
Conceptualization, H.Z. (He Zhang) and Y.G.; software, H.Z. (He Zhang) and H.Z. (Haifeng Zeng); validation, Y.G.; resources, H.Z. (He Zhang); data curation, C.S.; writing—original draft preparation, H.Z. (He Zhang); writing—review and editing, N.L. and Y.G.; project administration, C.S.; funding acquisition, Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 52065057.
Data Availability Statement
All relevant data presented in the article are stored according to institutional requirements and, as such, are not available online. However, all data used in this Manuscript can be made available upon request to the authors.
Acknowledgments
The authors present their appreciation to Shihezi University for funding this research through Researchers Supporting Program (Project number 52065057), Shihezi University, Shihezi, China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, W.; Jiao, H.; Liu, J.; Yang, S.; Chen, B.; Sun, W. Design of Safflower Filament Picking Device Based on TRIZ Theory. Trans. Chin. Soc. Agric. Mach. 2018, 49, 76–82. [Google Scholar]
- Chen, F.; Ge, Y.; Zhang, L.; Qi, Z.; Zeng, H. Design and experiment of the strip-collected pre-positioning mechanism for saf-flowerpicking robots. Trans. Chin. Soc. Agric. Eng. 2021, 37, 10–19. [Google Scholar]
- Huang, S.; Liu, H. Design and singularity analysis of a redundant actuated parallel mechanism. Mech. Sci. Tech. Aerosp. Eng. 2017, 36, 998–1004. [Google Scholar]
- Lee, J. Heterogeneous-ants-based path planner for global path planning of mobile robotapplications. Int. J. Control Autom. Syst. 2017, 15, 1754–1769. [Google Scholar] [CrossRef]
- Akka, K.; Khaber, F. Mobile robot path planning using an improved ant colony optimization. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418774673. [Google Scholar] [CrossRef] [Green Version]
- Chu, K.; Chang, T.; Wang, Q.; Yan, X. Path Planning Method of Ant Colony Algorithm Based on Effective Turning Point and Shortest-Minimum Path. Trans. Chin. Soc. Agric. Mach. 2021, 52, 400–407. [Google Scholar]
- Hou, W.; Xiong, Z.; Wang, C.; Chen, H. Enhanced ant colony algorithm with communication mechanism for mobile robot path planning. Robot. Auton. Syst. 2022, 148, 103949. [Google Scholar] [CrossRef]
- Jing, Y.; Jin, Z.; Liu, G. Three Dimensional Path Planning Method for Navigation of Farmland Leveling Based on Improved Ant Colony Algorithm. Trans. Chin. Soc. Agric. Mach. 2020, 51, 333–339. [Google Scholar]
- You, X.; Liu, S.; Lv, J. Ant colony algorithm based on dynamic search strategy and its application on path planning of robot. Control Decis. 2017, 32, 552–556. [Google Scholar]
- Cong, Z.; Wang, H.; Gao, M.; Li, J.; Wang, Z. Tomato Image Processing and Picking track Planning Based on Binocular Vision. Mach Tool. Hydraul. 2020, 48, 112–118. [Google Scholar]
- Liu, B.; Li, F.; Song, Z.; Liu, M.; Tian, F.; Zhao, Q.; Li, Y.; Yan, Y. Optimization of Cocoon-Picking Route of Mountage Cocoon Harvestor Based on Improved Max-Min Ant Colony Algorithm. Sci. Seric. 2021, 47, 435–442. [Google Scholar]
- Yang, J.; Sun, Z.; Wang, F. Optimal path control of parallel truss manipulator based on visual grasping. J. Comput. Appl. 2019, 39, 913–917. [Google Scholar]
- Xu, X.; Qian, Y.; Zhao, Y.; Zhang, Y.; Chen, X. Path optimization of three-dimensional warehouse based on improved ant colony algorithm. CIMS 2021, 27, 206–213. [Google Scholar]
- Zhang, S.; Wang, Y.; Chen, L.; Mo, H.; Cui, Y. Non-destructive Harvesting Path Planning of Multi Kiwi Fruit Based on Matlab. J. Agric. Mech. Res. 2019, 41, 18–23. [Google Scholar]
- Yuan, Y.; Zheng, X.; Lin, W. Path planning of picking robot for famous tea. J. Anhui Agric. Univ. 2017, 44, 530–535. [Google Scholar]
- Yang, H.; Chen, L.; Ma, Z.; Chen, M.; Zhong, Y.; Deng, F.; Li, M. Computer vision-based high-quality tea automatic plucking robot using Delta parallel manipulator. Comput. Electron. Agric. 2021, 181, 105946. [Google Scholar] [CrossRef]
- Zhang, X.; Ge, Y.; Zhang, L.; Chen, F.; Ma, W. Design and Experiment of Rectangular Safflower Picking Robot. J. Agric. Mech. Res. 2022, 44, 79–84. [Google Scholar]
- Zhang, T.; Zhang, L.; Ge, Y.; Liu, G.; Zhang, X. Development and Test of a Portable Roller–Type Safflower Harvester. J. Agric. Mech. Res. 2020, 3, 76–81. [Google Scholar]
- Yang, L.; Fu, L.; Guo, N.; Yang, Z.; Guo, H.; Xu, X. Path planning with multi-factor improved ant colony algorithm. CIMS 2022, 1–18. [Google Scholar]
- Wang, Q.; Zong, G.; Xu, J. Optimal Path Planning for Multi-stage Automatic Parking and Simulation Analysis. J. Syst. Simul. 2022, 34, 385–395. [Google Scholar]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- Yang, S. Design and Test of Comb-Type Safflower Picking Head Assembly. Master’s Dissertation, Shihezi University, Xinjiang, China, 2020. [Google Scholar]
- Ma, Z. Design and Research of Automatic Tea Picking Machine Based on Parallel Robot. Master’s Dissertation, Qingdao University of Science and Technology, Shandong, China, 2020. [Google Scholar]
- Liu, X.; Xie, T.; Xu, Y.; Wang, Y. Delta robot track planning based on synthetic motion. Manu. Auto. 2021, 43, 19–23+47. [Google Scholar]
- NY/T1133-2006; Operating Quality for Cotton Picker. National Agricultural Machinery Standardization Technical Committee: Washington, DC, USA, 2006.
Figure 1.
The overall structure of safflower picking robot. 1. Walking device; 2. Machine frame; 3. Fan; 4. Collecting box; 5. Collecting hose; 6. Dual rollers type end-effector; 7. Three-axis linear manipulator; 8. Visual recognition system; 9. Control box.
Figure 1.
The overall structure of safflower picking robot. 1. Walking device; 2. Machine frame; 3. Fan; 4. Collecting box; 5. Collecting hose; 6. Dual rollers type end-effector; 7. Three-axis linear manipulator; 8. Visual recognition system; 9. Control box.
Figure 2.
Effectiveness of picking safflower by dual rollers type end-effector: (a) Working principle diagram; (b) Effectiveness of picking tilting safflowers.
Figure 2.
Effectiveness of picking safflower by dual rollers type end-effector: (a) Working principle diagram; (b) Effectiveness of picking tilting safflowers.
Figure 3.
Morphological map of safflower plants: (a) Main view; (b) Vertical view.
Figure 3.
Morphological map of safflower plants: (a) Main view; (b) Vertical view.
Figure 4.
The tilting angle information of safflower.
Figure 4.
The tilting angle information of safflower.
Figure 5.
Comparison of two kinds of picking tracks: (a) Effectiveness of straight-line track; (b) Effectiveness of ∩-shaped track.
Figure 5.
Comparison of two kinds of picking tracks: (a) Effectiveness of straight-line track; (b) Effectiveness of ∩-shaped track.
Figure 6.
Comparison of two picking track models.
Figure 6.
Comparison of two picking track models.
Figure 7.
The fixed height ∩-shaped track model.
Figure 7.
The fixed height ∩-shaped track model.
Figure 8.
Secondary path optimization effect: (a) initial path planning; (b) secondary path optimization.
Figure 8.
Secondary path optimization effect: (a) initial path planning; (b) secondary path optimization.
Figure 9.
Flowchart of safflower picking path planning based on improved ACA.
Figure 9.
Flowchart of safflower picking path planning based on improved ACA.
Figure 10.
Simulation results of traditional ACA: (a) Path planning results; (b) Path length change curve; (c) Sum of waiting times of shortest paths.
Figure 10.
Simulation results of traditional ACA: (a) Path planning results; (b) Path length change curve; (c) Sum of waiting times of shortest paths.
Figure 11.
Simulation results of ACA with angle induction factor: (a) Path planning results; (b) Path length change curve; (c) Sum of the rotation time of shortest paths.
Figure 11.
Simulation results of ACA with angle induction factor: (a) Path planning results; (b) Path length change curve; (c) Sum of the rotation time of shortest paths.
Figure 12.
The fixed plane ∩-shaped track: (a) Simulation of picking path results; (b) Path length change curve.
Figure 12.
The fixed plane ∩-shaped track: (a) Simulation of picking path results; (b) Path length change curve.
Figure 13.
The fixed height ∩-shaped track: (a) Simulation of picking path results; (b) Path length change curve.
Figure 13.
The fixed height ∩-shaped track: (a) Simulation of picking path results; (b) Path length change curve.
Figure 14.
Optimal picking path from Initial path planning.
Figure 14.
Optimal picking path from Initial path planning.
Figure 15.
Result of the secondary path optimization.
Figure 15.
Result of the secondary path optimization.
Figure 16.
The fixed plane ∩-shaped picking track planning results: (a) Simulation of picking path results; (b) Path length change curve; (c) Sum of waiting times of shortest paths.
Figure 16.
The fixed plane ∩-shaped picking track planning results: (a) Simulation of picking path results; (b) Path length change curve; (c) Sum of waiting times of shortest paths.
Figure 17.
Improved ACA planning results: (a) Optimal picking path from initial path planning; (b) Result of secondary path optimization; (c) Path length change curved; (d) Sum of waiting times of shortest paths.
Figure 17.
Improved ACA planning results: (a) Optimal picking path from initial path planning; (b) Result of secondary path optimization; (c) Path length change curved; (d) Sum of waiting times of shortest paths.
Table 1.
ACA parameter value.
Table 1.
ACA parameter value.
| Parameters | Symbol | Value |
|---|
| Maximum number of iterations | G | 100 |
| The number of ants | m | 50 |
| Pheromone elicitation factor | α | 1 |
| Expected heuristic value | β | 5 |
| Pheromone enhancement coefficient | Q | 100 |
| Pheromone volatilization coefficient | | 0.25 |
Table 2.
Safflower parameter values.
Table 2.
Safflower parameter values.
| Parameter | Minimum | Maximum | Mean Value | Standard Deviation | Coefficient of Variation/% |
|---|
| Number of bulbs | 5 | 20 | 11 | 4.29 | 38.81 |
| Height difference between the highest bulb and the lowest bulb/cm | 8.1 | 28.9 | 17.4 | 6.44 | 36.99 |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).