Interval Forecasting Method of Aggregate Output for Multiple Wind Farms Using LSTM Networks and Time-Varying Regular Vine Copulas
Abstract
:1. Introduction
- (1)
- A time-varying regular vine copula model is proposed to obtain the conditional joint PDF of the forecasting errors of multiple wind farms. The proposed method not only uses multiple types of copula functions and optimize the structure of vine copula based on the Akaike information criterion (AIC), but also uses copula functions with time-varying dependence parameters to improve the model’s ability to capture the complex and time-varying correlations among multiple wind farms;
- (2)
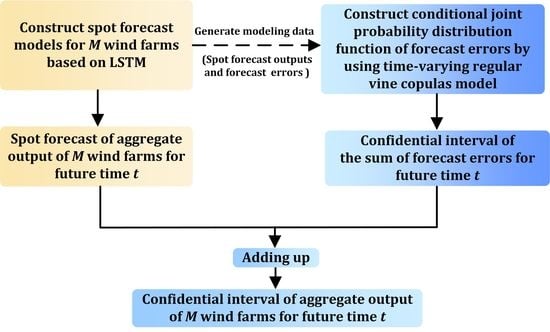
- Interval forecasting is achieved for the aggregate output for multiple wind farms by combining the spot forecasting model based on LSTM networks and the time-varying regular vine copula model. In this method, the historical outputs of multiple wind farms are used to train the spot forecasting model based on LSTM networks. Then, using the forecasting outputs and errors generated by the trained spot forecasting model as modeling data, a time-varying regular vine copula model is established to obtain the conditional joint PDF of the forecasting errors; then, the confidence interval can be derived from this model. Finally, the confidence intervals of the aggregate output are obtained by adding up the confidence intervals of forecasting errors and the spot forecasting outputs. This modeling framework can also be applied to combine the copula model with other spot forecasting methods.
2. Conditional Joint PDF for the Forecasting Errors of Multiple Wind Farms Using Time-Varying Regular Vine Copulas
2.1. Sklar’s Theorem
2.2. Regular Vine Copulas
2.3. Time-Varying Copula Functions
- (3)
- Time-varying Gaussian copula.
- (4)
- Time-varying t copula.
- (5)
- Time-varying Clayton copula.
- (6)
- Time-varying Gumbel copula.
- (7)
- Time-varying symmetrized Joe Clayton copula (SJC copula).
2.4. Modeling the Conditional Joint PDF for the Forecast Errors of Multiple Wind Farms Using Time-Varying Regular Vine Copulas
- 1.
- Fit the marginal distribution of the 2M variables. Kernel density estimation is used to fit the marginal PDFs of the 2M variables, and the estimation formula is as follows:where is the PDF of variable , h is the length of the sliding window, n is the sample numbers of samples of variable , and is the kernel function. The CDF of is obtained through a computing integral for ;
- 2.
- j = 1;
- 3.
- Form the node set for tree , and calculate the CDFs corresponding to the nodes in . If j = 1, then and the CDF corresponding to node i is . If j > 1, then ; the formula for calculating the CDFs corresponding to the nodes in is shown in reference [39];
- 4.
- Form all possible edge sets for tree ;
- 5.
- Construct bivariate copula models for each possible edge set. For each edge in a possible edge set, construct bivariate copula models by using five alternative types of time-varying copula functions and calculate the AIC indices of these models. The optimal model is selected as the final bivariate copula model corresponding to this edge. The AIC index calculation formula is as follows:where k is the number of model parameters and L is the likelihood. The smaller the AIC, the better the bivariate copula;
- 6.
- Choose the optimal edge set as the edge set for tree . The sum of the AICs of all edges in a possible edge set is used as the evaluation index, and the edge set with the smallest AIC is selected as the edge set for tree ;
- 7.
- Determine whether . If not, , calculate the node set for tree and return to 3; otherwise, proceed to 8;
- 8.
- Calculate the joint PDF of the spot forecasting outputs and errors of the M wind farms by using (3);
- 9.
- Calculate the conditional joint PDF of the forecasting errors of the M wind farms by using (16).
3. Interval Forecasting Method for the Aggregate Output of Multiple Wind Farms Using LSTM Networks and Time-varying Regular Vine Copulas
3.1. Interval Forecasting Method
- 1.
- Construct the spot forecasting model based on LSTM networks for M wind farms. First, the historical output data of the M wind farms are divided into a training set and a test set. The training dataset is used to train the LSTM networks, and the test dataset is used to verify the effectiveness of the model. Then, M LSTM networks are trained, and the LSTM network is trained for the wind farm, where . After training, the test dataset can be fed to the trained LSTM networks to obtain spot forecasting outputs for each wind farm. The spot forecasted aggregate output for the M wind farms is obtained by adding up the spot forecasting outputs of the M wind farms at the same moment;
- 2.
- Generate modeling data for the time-varying regular vine copula model based on the trained spot forecasting model. The test set of the spot model is divided into subsets A and B. The spot forecasting outputs and the errors of subset A generated by the trained spot forecasting model are used as modeling data to construct the TVRVC model, while subset B is used to test the effectiveness of the proposed method;
- 3.
- Construct the time-varying regular vine copula model for multiple wind farms, and obtain the conditional joint PDF of the forecasting errors;
- 4.
- Calculate the conditional joint PDF of the spot forecasting error corresponding to subset B. Input the spot forecasting outputs obtained for the M wind farms at the same moment belonging to subset B into the conditional joint PDF of the forecasting errors to obtain the conditional joint PDF of the forecasting errors for the corresponding moment;
- 5.
- Transform the conditional joint PDF of the forecasting errors into the conditional PDF of the sum of the forecasting errors by using the convolution formula [38];
- 6.
- Calculate the confidence interval of the sum of the forecasting errors at the given confidence level;
- 7.
- Calculate the forecasting interval for the aggregate output of the M wind farms. This interval is obtained by adding the confidence interval of the sum of the forecasting errors to the corresponding spot forecasted aggregate output.
3.2. Evaluation Indices
4. Results and Discussion
4.1. Spot Forecasting Results and Discussion
4.2. Structures of the Time-Varying Regular Vine Copulas for the Three Wind Farms
4.3. Interval Forecasting Results and Discussion
- BP networks and time-varying regular vine copulas (BP-TVRVC) method: The forecast error data generated by BP networks are used for time-varying regular vine copulas modeling, and the RMSE of the BP networks is shown in Table 2.
- LSTM networks and time-varying copulas (LSTM-TVC) method: This is a superposition method. After performing spot forecasting with the LSTM networks, modeling the time-varying bivariate copula of the spot forecasting outputs and forecasting errors for each wind farm to obtain their respective forecasting intervals, the forecast intervals are superimposed as their aggregate output interval. This method ignores the spatial correlation between multiple wind farms.
- LSTM networks and static regular vine copulas (LSTM-SRVC) method: LSTM networks are still used for spot forecasting, but the time-varying copula functions used in the time-varying regular vine copula model are replaced by the corresponding static copula functions. This method considers the correlations among the outputs of multiple wind farms but does not consider the time-varying nature of the correlations; this method was also used in ref. [37].
- LSTM networks and time-varying regular vine Gaussian copulas (LSTM-TVRVGC) method: After the LSTM networks are used for the spot forecasting, the regular vine copula model is constructed with the time-varying Gaussian copulas. This method corresponds to the method used in [38].
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, B.; Ma, X.; Luo, Y.; Yang, D. Wind Power Prediction Based on LSTM Networks and Nonparametric Kernel Density Estimation. IEEE Access 2019, 7, 165279–165292. [Google Scholar] [CrossRef]
- Zhao, C.; Wan, C.; Song, Y. Operating Reserve Quantification Using Prediction Intervals of Wind Power: An Integrated Probabilistic Forecasting and Decision Methodology. IEEE Trans. Power Syst. 2021, 36, 3701–3714. [Google Scholar] [CrossRef]
- He, Y.; Li, H. Probability density forecasting of wind power using quantile regression neural network and kernel density estimation. Energy Convers. Manag. 2018, 164, 374–384. [Google Scholar] [CrossRef]
- Haque, A.U.; Nehrir, M.H.; Mandal, P. A Hybrid Intelligent Model for Deterministic and Quantile Regression Approach for Probabilistic Wind Power Forecasting. IEEE Trans. Power Syst. 2014, 29, 1663–1672. [Google Scholar] [CrossRef]
- Wan, C.; Lin, J.; Wang, J.; Song, Y.; Dong, Z.Y. Direct Quantile Regression for Nonparametric Probabilistic Forecasting of Wind Power Generation. IEEE Trans. Power Syst. 2016, 32, 2767–2778. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, M.; Han, X.; Zhang, Y.; Ye, P. A Regional Wind Power Probabilistic Forecast Method Based on Deep Quantile Regression. IEEE Trans. Ind. Appl. 2021, 57, 4420–4427. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, B.; Guo, S.; Watada, J. Multi-objective prediction intervals for wind power forecast based on deep neural networks. Inf. Sci. 2020, 550, 207–220. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, C.; Song, Y. Chance Constrained Extreme Learning Machine for Nonparametric Prediction Intervals of Wind Power Generation. IEEE Trans. Power Syst. 2020, 35, 3869–3884. [Google Scholar] [CrossRef]
- Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A Short-Term Wind Power Forecasting Approach with Adjustment of Numerical Weather Prediction Input by Data Mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291. [Google Scholar] [CrossRef]
- Safari, N.; Chung, C.Y.; Price, G.C.D. Novel Multi-Step Short-Term Wind Power Prediction Framework Based on Chaotic Time Series Analysis and Singular Spectrum Analysis. IEEE Trans. Power Syst. 2017, 33, 590–601. [Google Scholar] [CrossRef]
- Bizrah, A.; Almuhaini, M. Modeling wind speed using probability distribution function, Markov and ARMA models. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Ekanayake, P.; Peiris, A.T.; Jayasinghe, J.M.J.W.; Rathnayake, U. Development of Wind Power Prediction Models for Pawan Danavi Wind Farm in Sri Lanka. Math. Probl. Eng. 2021, 2021, 4893713. [Google Scholar] [CrossRef]
- Ibrahim, M.; Alsheikh, A.; Al-Hindawi, Q.; Al-Dahidi, S.; ElMoaqet, H. Short-Time Wind Speed Forecast Using Artificial Learning-Based Algorithms. Comput. Intell. Neurosci. 2020, 2020, 8439719. [Google Scholar] [CrossRef] [PubMed]
- Akbal, Y.; Ünlü, K.D. A univariate time series methodology based on sequence-to-sequence learning for short to midterm wind power production. Renew. Energy 2022, 200, 832–844. [Google Scholar] [CrossRef]
- Farah, S.; David, A.W.; Humaira, N.; Aneela, Z.; Steffen, E. Short-term multi-hour ahead country-wide wind power prediction for Germany using gated recurrent unit deep learning. Renew. Sustain. Energy Rev. 2022, 167, 112700. [Google Scholar] [CrossRef]
- Abualigah, L.; Abu Zitar, R.; Almotairi, K.H.; Hussein, A.M.; Elaziz, M.A.; Nikoo, M.R.; Gandomi, A.H. Wind, Solar, and Photovoltaic Renewable Energy Systems with and without Energy Storage Optimization: A Survey of Advanced Machine Learning and Deep Learning Techniques. Energies 2022, 15, 578. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Zhao, Y.; Pan, G. Wind Speed Prediction of IPSO-BP Neural Network Based on Lorenz Disturbance. IEEE Access 2018, 6, 53168–53179. [Google Scholar] [CrossRef]
- Tian, W.; Bao, Y.; Liu, W. Wind Power Forecasting by the BP Neural Network with the Support of Machine Learning. Math. Probl. Eng. 2022, 2022, 7952860. [Google Scholar] [CrossRef]
- Yang, L.; He, M.; Zhang, J.; Vittal, V. Support-Vector-Machine-Enhanced Markov Model for Short-Term Wind Power Forecast. IEEE Trans. Sustain. Energy 2015, 6, 791–799. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Jiang, M.; Yuan, Y. Prediction interval of wind power using parameter optimized Beta distribution based LSTM model. Appl. Soft Comput. 2019, 82, 105550. [Google Scholar] [CrossRef]
- Yuan, C.; Tang, Y.; Mei, R.; Mo, F.; Wang, H. A PSO-LSTM Model of Offshore Wind Power Forecast considering the Variation of Wind Speed in Second-Level Time Scale. Math. Probl. Eng. 2021, 2021, 2009062. [Google Scholar] [CrossRef]
- Santhosh, M.; Venkaiah, C.; Kumar, D.V. Short-term wind speed forecasting approach using Ensemble Empirical Mode Decomposition and Deep Boltzmann Machine. Sustain. Energy Grids Netw. 2019, 19, 100242. [Google Scholar] [CrossRef]
- Yan, J.; Li, K.; Bai, E.-W.; Deng, J.; Foley, A.M. Hybrid Probabilistic Wind Power Forecasting Using Temporally Local Gaussian Process. IEEE Trans. Sustain. Energy 2015, 7, 87–95. [Google Scholar] [CrossRef]
- Kou, P.; Gao, F.; Guan, X.; Wu, J. Prediction intervals for wind power forecasting: Using sparse warped Gaussian process. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Yang, H.; Yuan, J.; Zhang, T. A model and algorithm for minimum probability interval of wind power forecast errors based on Beta distribution. Proc. CSEE 2015, 35, 2135–2142. [Google Scholar] [CrossRef]
- Lan, F.; Sang, C.; Liang, J.; Li, J. Interval prediction for wind power based on conditional Copula function. Proc. CSEE 2016, 36, 79–86. [Google Scholar] [CrossRef]
- Quan, H.; Khosravi, A.; Yang, D.; Srinivasan, D. A Survey of Computational Intelligence Techniques for Wind Power Uncertainty Quantification in Smart Grids. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 4582–4599. [Google Scholar] [CrossRef] [PubMed]
- Davidson, M.R.; Zhang, D.; Xiong, W.; Zhang, X.; Karplus, V.J. Modelling the potential for wind energy integration on China’s coal-heavy electricity grid. Nat. Energy 2016, 1, 16086. [Google Scholar] [CrossRef]
- Kang, C.; Yao, L. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy. Autom. Electr. Power Syst. 2017, 41, 2–11. [Google Scholar]
- Peng, X.; Chen, Y.; Cheng, K.; Wang, H.; Zhao, Y.; Wang, B.; Che, J.; Liu, C.; Wen, J.; Lu, C.; et al. Wind Power Prediction for Wind Farm Clusters Based on the Multifeature Similarity Matching Method. IEEE Trans. Ind. Appl. 2020, 56, 4679–4688. [Google Scholar] [CrossRef]
- Andrade, J.R.; Bessa, R.J. Improving Renewable Energy Forecasting with a Grid of Numerical Weather Predictions. IEEE Trans. Sustain. Energy 2017, 8, 1571–1580. [Google Scholar] [CrossRef]
- Lobo, M.G.; Sanchez, I. Regional Wind Power Forecasting Based on Smoothing Techniques, With Application to the Spanish Peninsular System. IEEE Trans. Power Syst. 2012, 27, 1990–1997. [Google Scholar] [CrossRef]
- Peng, X.; Xiong, L.; Wen, J.; Cheng, S.; Wang, B. A Summary of the State of the Art for Short-term and Ultra-short-term Wind Power Prediction of Regions. Proc. CSEE 2016, 36, 6315–6326. [Google Scholar] [CrossRef]
- Zhang, N.; Kang, C.; Xia, Q.; Liang, J. Modeling Conditional Forecast Error for Wind Power in Generation Scheduling. IEEE Trans. Power Syst. 2014, 29, 1316–1324. [Google Scholar] [CrossRef]
- Alexiadis, M.; Dokopoulos, P.; Sahsamanoglou, H. Wind speed and power forecasting based on spatial correlation models. IEEE Trans. Energy Convers. 1999, 14, 836–842. [Google Scholar] [CrossRef]
- Yunus, K.; Chen, P.; Thiringer, T. Modelling spatially and temporally correlated wind speed time series over a large geographical area using VARMA. IET Renew. Power Gener. 2016, 11, 132–142. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, W.; Liu, C.; Wang, Z.; Hou, Y. Probabilistic Forecast for Multiple Wind Farms Based on Regular Vine Copulas. IEEE Trans. Power Syst. 2017, 33, 578–589. [Google Scholar] [CrossRef]
- Duan, S.; Miao, S.; Lixing, L.I.; Han, J.; Qingyu, T.U.; Yaowang, L.I. Uncertainty Model of Combined Output for Multiple Wind Farms Considering Dynamic Correlation of Prediction Errors. Autom. Electr. Power Syst. 2019, 43, 31–37. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Kurowicka, D.; Joe, H. Dependence Modeling: Vine Copula Handbook; World Scientific: Singapore, 2010. [Google Scholar] [CrossRef]
- Attoh-Okine, N. Copula Models. In Big Data and Differential Privacy; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 175–195. [Google Scholar] [CrossRef]
- Patton, A.J. Modelling Time-Varying Exchange Rate Dependence Using the Conditional Copula. SSRN Electron. J. 2001. [Google Scholar] [CrossRef]
- Patton, A.J. On the Out-of-Sample Importance of Skewness and Asymmetric Dependence for Asset Allocation. J. Financ. Econ. 2004, 2, 130–168. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. A novel genetic LSTM model for wind power forecast. Energy 2021, 223, 120069. [Google Scholar] [CrossRef]
- Hossain, M.A.; Chakrabortty, R.K.; Elsawah, S.; Gray, E.; Ryan, M.J. Predicting Wind Power Generation Using Hybrid Deep Learning with Optimization. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Dong, W.; Sun, H.; Tan, J.; Li, Z.; Zhang, J.; Yang, H. Regional wind power probabilistic forecasting based on an improved kernel density estimation, regular vine copulas, and ensemble learning. Energy 2022, 238, 122045. [Google Scholar] [CrossRef]








| Wind Farm 1 and 2 | Wind Farm 1 and 3 | Wind Farm 2 and 3 | |
|---|---|---|---|
| Kendall’s tau coefficients | 0.944 | 0.907 | 0.888 |
| RMSE(MW) | |||||
|---|---|---|---|---|---|
| Dataset 1 | Dataset 2 | Dataset 3 | Dataset 4 | ||
| LSTM | Wind Farm 1 | 2.2742 | 2.3768 | 2.5133 | 2.1485 |
| Wind Farm 2 | 2.4184 | 2.4868 | 2.5812 | 2.2508 | |
| Wind Farm 3 | 2.5702 | 2.7155 | 2.7471 | 2.4642 | |
| BP | Wind Farm 1 | 3.4114 | 3.5652 | 3.7699 | 3.2227 |
| Wind Farm 2 | 3.6276 | 3.7301 | 3.8717 | 3.3762 | |
| Wind Farm 3 | 3.8554 | 4.0732 | 4.1206 | 3.6962 | |
| AIC (×103) | |||||
|---|---|---|---|---|---|
| Gaussian | t | Clayton | Gumbel | SJC | |
| 1,2 | −6.105 | −6.222 | −8.204 | −7.074 | −7.673 |
| 5,2|1 | −0.177 | −0.306 | −0.744 | −0.163 | −0.823 |
| Nominal Confidence | SS | ||||
|---|---|---|---|---|---|
| LSTM-TVRVC | BP-TVRVC | LSTM-TVC | LSTM-SRVC | LSTM-TVRVGC | |
| 90% | −1.325 | −1.984 | −1.454 | −1.504 | −1.384 |
| 80% | −2.016 | −2.998 | −2.093 | −2.211 | −2.121 |
| 70% | −2.439 | −3.728 | −2.544 | −2.705 | −2.644 |
| 60% | −2.808 | −4.273 | −2.882 | −3.051 | −3.013 |
| 50% | −3.021 | −4.694 | −3.138 | −3.292 | −3.263 |
| 40% | −3.185 | −4.995 | −3.334 | −3.444 | −3.411 |
| 30% | −3.329 | −5.201 | −3.476 | −3.524 | −3.482 |
| 20% | −3.400 | −5.328 | −3.573 | −3.554 | −3.508 |
| 10% | −3.444 | −5.395 | −3.624 | −3.566 | −3.513 |
| mean | −2.774 | −4.288 | −2.902 | −2.983 | −2.927 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Sun, Y.; Li, Y.; Feng, C.; Chen, P. Interval Forecasting Method of Aggregate Output for Multiple Wind Farms Using LSTM Networks and Time-Varying Regular Vine Copulas. Processes 2023, 11, 1530. https://doi.org/10.3390/pr11051530
Wang Y, Sun Y, Li Y, Feng C, Chen P. Interval Forecasting Method of Aggregate Output for Multiple Wind Farms Using LSTM Networks and Time-Varying Regular Vine Copulas. Processes. 2023; 11(5):1530. https://doi.org/10.3390/pr11051530
Chicago/Turabian StyleWang, Yanwen, Yanying Sun, Yalong Li, Chen Feng, and Peng Chen. 2023. "Interval Forecasting Method of Aggregate Output for Multiple Wind Farms Using LSTM Networks and Time-Varying Regular Vine Copulas" Processes 11, no. 5: 1530. https://doi.org/10.3390/pr11051530
APA StyleWang, Y., Sun, Y., Li, Y., Feng, C., & Chen, P. (2023). Interval Forecasting Method of Aggregate Output for Multiple Wind Farms Using LSTM Networks and Time-Varying Regular Vine Copulas. Processes, 11(5), 1530. https://doi.org/10.3390/pr11051530