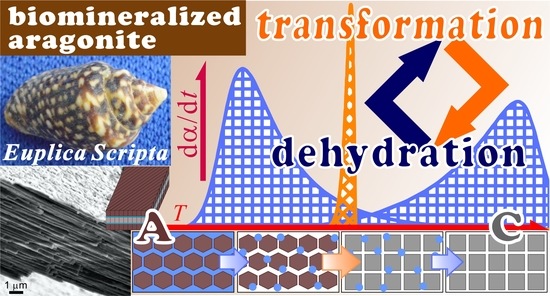
Interplay between Thermally Induced Aragonite–Calcite Transformation and Multistep Dehydration in a Seawater Spiral Shell (Euplica scripta)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample and Characterization
2.2. Investigation of Thermal Behavior
2.3. Kinetic Data Measurement for the A–C Transformation
2.4. Kinetic Data Measurement for the Multistep Thermal Dehydration
3. Results and Discussion
3.1. Sample Characterization
3.2. Thermal Behavior
3.3. Kinetics of the A–C Transformation
3.4. Kinetics of the Multistep Thermal Dehydration
3.5. Kinetic Relationship between A–C Transformation and Multistep Thermal Dehydration
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mann, S. Biomineralization: Principles and Concepts in Bioinorganic Materials Chemistry; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Fujinuki, T.; Igarashi, T. On the water in the hexacollara. J. Jpn. Assoc. Mineral. Petrol. Econ. Geol. 1969, 62, 1–17. [Google Scholar] [CrossRef]
- Yoshioka, S.; Kitano, Y. Transformation of aragonite to calcite through heating. Geochem. J. 1985, 19, 245–249. [Google Scholar] [CrossRef]
- Baumer, A.; Ganteaume, M.; Bernat, M. Variations de la teneur en eau des coraux lors de la transformation aragonite → calcite. Thermochim. Acta 1993, 221, 255–262. [Google Scholar] [CrossRef]
- Passe-Coutrin, N.; N’Guyen, P.; Pelmard, R.; Ouensanga, A.; Bouchon, C. Water desorption and aragonite—Calcite phase transition in scleractinian corals skeletons. Thermochim. Acta 1995, 265, 135–140. [Google Scholar] [CrossRef]
- Ganteaume, M.; Baumer, A.; Lapraz, D.; Iacconi, P.; Bokilo, J.-E.; Bernat, M.; Zahra, C. La transformation aragonite-calcite dans les coraux fossiles. relation avec la thermoluminescence. Thermochim. Acta 1990, 170, 121–137. [Google Scholar] [CrossRef]
- Perić, J.; Vučak, M.; Krstulović, R.; Brečević, L.; Kralj, D. Phase transformation of calcium carbonate polymorphs. Thermochim. Acta 1996, 277, 175–186. [Google Scholar] [CrossRef]
- Koga, N.; Kasahara, D.; Kimura, T. Aragonite Crystal Growth and Solid-State Aragonite–Calcite Transformation: A Physico–Geometrical Relationship via Thermal Dehydration of Included Water. Cryst. Growth Des. 2013, 13, 2238–2246. [Google Scholar] [CrossRef]
- Dasgupta, D.R. The oriented transformation of aragonite into calcite. Mineral. Mag. J. Mineral. Soc. 1964, 33, 924–928. [Google Scholar] [CrossRef]
- Antao, S.M.; Hassan, I. Temperature dependence of the structural parameters in the transformation of aragonite to calcite, as determined from in situ synchrotron powder X-ray-diffraction data. Can. Mineral. 2010, 48, 1225–1236. [Google Scholar] [CrossRef]
- Kôzu, S.; Kani, K. Thermal expansion of aragonite and its atomic displacements by transformation into calcite between 450 °C and 490 °C in air, I. Proc. Imp. Acad. 1934, 10, 222–225. [Google Scholar] [CrossRef]
- Lucas, A.; Mouallem-Bahout, M.; Carel, C.; Gaudé, J.; Matecki, M. Thermal expansion of synthetic aragonite condensed review of elastic properties. J. Solid State Chem. 1999, 146, 73–78. [Google Scholar] [CrossRef]
- Parker, J.E.; Thompson, S.P.; Lennie, A.R.; Potter, J.; Tang, C.C. A study of the aragonite-calcite transformation using Raman spectroscopy, synchrotron powder diffraction and scanning electron microscopy. CrystEngComm 2010, 12, 1590–1599. [Google Scholar] [CrossRef]
- Irigaray, J.L.; Oudadesse, H.; El Fadl, H.; Sauvage, T.; Thomas, G.; Vernay, A.M. Effet de la temperature sur la structure cristalline d’un biocorail. J. Therm. Anal. 1993, 39, 3–14. [Google Scholar] [CrossRef]
- Zolotoyabko, E.; Pokroy, B. Biomineralization of calcium carbonate: Structural aspects. CrystEngComm 2007, 9, 1156–1161. [Google Scholar] [CrossRef]
- Pokroy, B.; Fitch, A.N.; Lee, P.L.; Quintana, J.P.; Caspi, E.N.; Zolotoyabko, E. Anisotropic lattice distortions in the mollusk-made aragonite: A widespread phenomenon. J. Struct. Biol. 2006, 153, 145–150. [Google Scholar] [CrossRef] [PubMed]
- Pokroy, B.; Quintana, J.P.; Caspi, E.N.; Berner, A.; Zolotoyabko, E. Anisotropic lattice distortions in biogenic aragonite. Nat. Mater. 2004, 3, 900–902. [Google Scholar] [CrossRef] [PubMed]
- Kamat, S.; Su, X.; Ballarini, R.; Heuer, A.H. Structural basis for the fracture toughness of the shell of the conch Strombus gigas. Nature 2000, 405, 1036–1040. [Google Scholar] [CrossRef]
- Ji, H.-M.; Jiang, Y.; Yang, W.; Zhang, G.-P.; Li, X.-W. Biological self-arrangement of fiber like aragonite and its effect on mechanical behavior of Veined rapa whelk shell. J. Am. Ceram. Soc. 2015, 98, 3319–3325. [Google Scholar] [CrossRef]
- Pokroy, B.; Zolotoyabko, E. Microstructure of natural plywood-like ceramics: A study by high-resolution electron microscopy and energy-variable X-ray diffraction. J. Mater. Chem. 2003, 13, 682–688. [Google Scholar] [CrossRef]
- Pavat, C.; Zanella-Cléon, I.; Becchi, M.; Medakovic, D.; Luquet, G.; Guichard, N.; Alcaraz, G.; Dommergues, J.L.; Serpentini, A.; Lebel, J.M.; et al. The shell matrix of the pulmonate land snail Helix aspersa maxima. Comp. Biochem. Physiol. Part B Biochem. Mol. Biol. 2012, 161, 303–314. [Google Scholar] [CrossRef]
- Koga, N.; Nishikawa, K. Mutual relationship between solid-state aragonite–calcite transformation and thermal dehydration of included water in coral aragonite. Cryst. Growth Des. 2014, 14, 879–887. [Google Scholar] [CrossRef]
- Tone, T.; Koga, N. Thermally induced aragonite-calcite transformation in freshwater pearl: A mutual relation with the thermal dehydration of included water. ACS Omega 2021, 6, 13904–13914. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Jiménez, P.E.; Perejón, A.; Criado, J.M.; Diánez, M.J.; Pérez-Maqueda, L.A. Kinetic model for thermal dehydrochlorination of poly(vinyl chloride). Polymer 2010, 51, 3998–4007. [Google Scholar] [CrossRef]
- Koga, N.; Goshi, Y.; Yamada, S.; Pérez-Maqueda, L.A. Kinetic approach to partially overlapped thermal decomposition processes. J. Therm. Anal. Calorim. 2013, 111, 1463–1474. [Google Scholar] [CrossRef]
- Koga, N. Physico-Geometric Approach to the Kinetics of Overlapping Solid-State Reactions. In Handbook of Thermal Analysis and Calorimetry, 2nd ed.; Vyazovkin, S., Koga, N., Schick, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 6, pp. 213–251. [Google Scholar]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Perez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Koga, N.; Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Muravyev, N.V.; Pérez-Maqueda, L.A.; Saggese, C.; Sánchez-Jiménez, P.E. ICTAC Kinetics Committee recommendations for analysis of thermal decomposition kinetics. Thermochim. Acta 2023, 719, 179384. [Google Scholar] [CrossRef]
- Sugiyama, S.; Takasaki, M.; Oaki, Y.; Imai, H. Strained calcite crystals from amorphous calcium carbonate containing an organic molecule. CrystEngComm 2020, 22, 7054–7058. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, G.; Du, J.; Zhao, Q.; Pei, X. 1,1′-Ferrocenedicarboxylic acid/tetrahydrofuran induced precipitation of calcium carbonate with a multi-level structure in water. CrystEngComm 2021, 23, 7206–7211. [Google Scholar] [CrossRef]
- Nagai, Y.; Oaki, Y.; Imai, H. Artificial mineral films similar to biogenic calcareous shells: Oriented calcite nanorods on a self-standing polymer sheet. CrystEngComm 2018, 20, 1656–1661. [Google Scholar] [CrossRef]
- Buljan Meić, I.; Kontrec, J.; Domazet Jurašin, D.; Njegić Džakula, B.; Štajner, L.; Lyons, D.M.; Dutour Sikirić, M.; Kralj, D. Comparative study of calcium carbonates and calcium phosphates precipitation in model systems mimicking the inorganic environment for biomineralization. Cryst. Growth Des. 2017, 17, 1103–1117. [Google Scholar] [CrossRef]
- Morse, J.W.; Arvidson, R.S.; Luttge, A. Calcium carbonate formation and dissolution. Chem. Rev. 2007, 107, 342–381. [Google Scholar] [CrossRef] [PubMed]
- Meldrum, F.C.; Colfen, H. Controlling mineral morphologies and structures in biological and synthetic systems. Chem. Rev. 2008, 108, 4332–4432. [Google Scholar] [CrossRef] [PubMed]
- Sommerdijk, N.A.; de With, G. Biomimetic CaCO3 mineralization using designer molecules and interfaces. Chem. Rev. 2008, 108, 4499–4550. [Google Scholar] [CrossRef] [PubMed]
- Sugiura, M.; Yasumoto, K.; Iijima, M.; Oaki, Y.; Imai, H. Morphological study of fibrous aragonite in the skeletal framework of a stony coral. CrystEngComm 2021, 23, 3693–3700. [Google Scholar] [CrossRef]
- Nakajima, K.; Suzuki, M.; Nagai, Y.; Izumida, K.; Oaki, Y.; Toyofuku, T.; Bijma, J.; Nehrke, G.; Raitzsch, M.; Tani, K.; et al. Hierarchical textures on aragonitic shells of the hyaline radial foraminifer Hoeglundina elegans. CrystEngComm 2017, 19, 7191–7196. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, G. New insights into the spatial confinement mechanism of nucleation of biogenic aragonite crystals from bivalve nacre. CrystEngComm 2020, 22, 6596–6602. [Google Scholar] [CrossRef]
- De Villie, J.P.R. Crystal structures of aragonite, strontianite, and witherite. Am. Mineral. 1971, 56, 758–767. [Google Scholar]
- Caspi, E.N.; Pokroy, B.; Lee, P.L.; Quintana, J.P.; Zolotoyabko, E. On the structure of aragonite. Acta Crystallogr. B 2005, 61, 129–132. [Google Scholar] [CrossRef]
- Markgraf, S.A.; Reeder, R.J. High-temperature structure refinements of calcite and magnesite. Am. Mineral. 1985, 70, 590–600. [Google Scholar]
- Andersen, F.; Brecevic, L. Infrared spectra of amorphous and crystalline calcium carbonates. Acta Chem. Scand. 1991, 45, 1018–1024. [Google Scholar] [CrossRef]
- Vagenas, N.V.; Gatsouli, A.; Kontoyannis, C.G. Quantitative analysis of synthetic calcium carbonate polymorphs using FT-IR spectroscopy. Talanta 2003, 59, 831–836. [Google Scholar] [CrossRef] [PubMed]
- De Lorenzi Pezzolo, A. The shell seeker: What is the quantity of shell in the Lido di Venezia Sand? A calibration DRIFTS experiment. J. Chem. Educ. 2011, 88, 1298–1303. [Google Scholar] [CrossRef]
- Loftus, E.; Rogers, K.; Lee-Thorp, J. A simple method to establish calcite:aragonite ratios in archaeological mollusc shells. J. Quat. Sci. 2015, 30, 731–735. [Google Scholar] [CrossRef]
- De Lorenzi Pezzolo, A. An exercise on calibration: DRIFTS study of binary mixtures of calcite and dolomite with partially overlapping spectral features. J. Chem. Educ. 2013, 90, 118–122. [Google Scholar] [CrossRef]
- Toffolo, M.; Regev, L.; Dubernet, S.; Lefrais, Y.; Boaretto, E. FTIR-based crystallinity assessment of aragonite–calcite mixtures in archaeological lime binders altered by diagenesis. Minerals 2019, 9, 121. [Google Scholar] [CrossRef]
- Compere, E.L.; Bates, J.M. Determination of calcite: Aragonite ratios in mollusc shells by infrared spectra. Limnol. Oceanogr. 1973, 18, 326–331. [Google Scholar] [CrossRef]
- Xyla, A.G.; Koutsoukos, P.G. Quantitative analysis of calcium carbonate polymorphs by infrared spectroscopy. J. Chem. Soc. Faraday Trans. 1 1989, 85, 3165–3172. [Google Scholar] [CrossRef]
- Tsuboi, Y.; Koga, N. Thermal decomposition of biomineralized calcium carbonate: Correlation between the thermal behavior and structural characteristics of avian eggshell. ACS Sustain. Chem. Eng. 2018, 6, 5283–5295. [Google Scholar] [CrossRef]
- Koga, N.; Šesták, J.; Simon, P. Some fundamental and historical aspects of phenomenological kinetics in the solid state studied by thermal analysis. In Thermal Analysis of Micro, Nano- and Non-Crystalline Materials; Šesták, J., Simon, P., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 1–28. [Google Scholar]
- Coats, A.W.; Redfern, J.P. Kinetic parameters from thermogravimetric data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Tanaka, H.; Koga, N. Kinetics of the thermal decompositions of MC2O4 to MCO3 (M = Ca, Sr and Ba). J. Therm. Anal. 1987, 32, 1521–1529. [Google Scholar] [CrossRef]
- Koga, N.; Tanaka, H. Kinetics of Thermal Decomposition of MCO3 to MO (M = Ca, Sr and Ba). J. Therm. Anal. 1988, 34, 177–188. [Google Scholar] [CrossRef]
- Tanaka, H.; Koga, N. Kinetics of the thermal dehydration of potassium copper(II) chloride dihydrate. J. Phys. Chem. 1988, 92, 7023–7029. [Google Scholar] [CrossRef]
- Koga, N.; Tanaka, H. Kinetics and mechanisms of the thermal dehydration of Li2SO4·H2O. J. Phys. Chem. 1989, 93, 7793–7798. [Google Scholar] [CrossRef]
- Criado, J.M.; Gonzalez, M. The method of calculation of kinetic parameters as a possible cause of apparent compensation effects. Thermochim. Acta 1981, 46, 201–207. [Google Scholar] [CrossRef]
- Koga, N.; Šesták, J.; Málek, J. Distortion of the Arrhenius Parameters by the Inappropriate Kinetic-Model Function. Thermochim. Acta 1991, 188, 333–336. [Google Scholar] [CrossRef]
- Koga, N.; Tanaka, H. A Kinetic compensation effect established for the thermal decomposition of a solid. J. Therm. Anal. 1991, 37, 347–363. [Google Scholar] [CrossRef]
- Koga, N.; Šesták, J. Kinetic compensation effect as a mathematical consequence of the exponential rate constant. Thermochim. Acta 1991, 182, 201–208. [Google Scholar] [CrossRef]
- Koga, N.; Šesták, J. Further aspects of the kinetic compensation effect. J. Therm. Anal. 1991, 37, 1103–1108. [Google Scholar] [CrossRef]
- Koga, N. A review of the mutual dependence of Arrhenius parameters evaluated by the thermoanalytical study of solid-state reactions: The kinetic compensation effect. Thermochim. Acta 1994, 244, 1–20. [Google Scholar] [CrossRef]
- Galwey, A.K.; Mortimer, M. Compensation effects and compensation defects in kinetic and mechanistic interpretations of heterogeneous chemical reactions. Int. J. Chem. Kinet. 2006, 38, 464–473. [Google Scholar] [CrossRef]
- Barrie, P.J. The mathematical origins of the kinetic compensation effect: 1. The effect of random experimental errors. Phys. Chem. Chem. Phys. 2012, 14, 318–326. [Google Scholar] [CrossRef]
- Barrie, P.J. The mathematical origins of the kinetic compensation effect: 2. The effect of systematic errors. Phys. Chem. Chem. Phys. 2012, 14, 327–336. [Google Scholar] [CrossRef]
- Xu, D.; Chai, M.; Dong, Z.; Rahman, M.M.; Yu, X.; Cai, J. Kinetic compensation effect in logistic distributed activation energy model for lignocellulosic biomass pyrolysis. Bioresour. Technol. 2018, 265, 139–145. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Ozawa, T. Kinetic analysis of derivative curves in thermal analysis. J. Therm. Anal. 1970, 2, 301–324. [Google Scholar] [CrossRef]
- Ozawa, T. Applicability of Friedman plot. J. Therm. Anal. 1986, 31, 547–551. [Google Scholar] [CrossRef]
- Málek, J. The kinetic analysis of non-isothermal data. Thermochim. Acta 1992, 200, 257–269. [Google Scholar] [CrossRef]
- Koga, N. Kinetic analysis of thermoanalytical data by extrapolating to infinite temperature. Thermochim. Acta 1995, 258, 145–159. [Google Scholar] [CrossRef]
- Gotor, F.J.; Criado, J.M.; Málek, J.; Koga, N. Kinetic analysis of solid-state reactions: The universality of master plots for analyzing isothermal and nonisothermal experiments. J. Phys. Chem. A 2000, 104, 10777–10782. [Google Scholar] [CrossRef]
- Criado, J.M.; Pérez-Maqueda, L.A.; Gotor, F.J.; Málek, J.; Koga, N. A unified theory for the kinetic analysis of solid state reactions under any thermal pathway. J. Therm. Anal. Calorim. 2003, 72, 901–906. [Google Scholar] [CrossRef]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Ozawa, T. Non-isothermal kinetics and generalized time. Thermochim. Acta 1986, 100, 109–118. [Google Scholar] [CrossRef]
- Šesták, J.; Berggren, G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures. Thermochim. Acta 1971, 3, 1–12. [Google Scholar] [CrossRef]
- Šesták, J. Diagnostic limits of phenomenological kinetic models introducing the accommodation function. J. Therm. Anal. 1990, 36, 1997–2007. [Google Scholar] [CrossRef]
- Šesták, J. Rationale and fallacy of thermoanalytical kinetic patterns. J. Therm. Anal. Calorim. 2011, 110, 5–16. [Google Scholar] [CrossRef]
- Perejón, A.; Sánchez-Jiménez, P.E.; Criado, J.M.; Pérez-Maqueda, L.A. Kinetic analysis of complex solid-state reactions. A new deconvolution procedure. J. Phys. Chem. B 2011, 115, 1780–1791. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, R.; Málek, J. Applicability of Fraser–Suzuki function in kinetic analysis of complex crystallization processes. J. Therm. Anal. Calorim. 2013, 111, 1045–1056. [Google Scholar] [CrossRef]
- Tatsuoka, T.; Koga, N. Effect of atmospheric water vapor on the thermally induced crystallization in zirconia gel. J. Am. Ceram. Soc. 2012, 95, 557–564. [Google Scholar] [CrossRef]
- Mansour, S.A. Non-isothermal crystallization kinetics of nano-sized amorphous TiO2 prepared by facile sonochemical hydrolysis route. Ceram. Int. 2019, 45, 2893–2898. [Google Scholar] [CrossRef]











| g(αtr) | Ea,tr/kJ mol−1 | ln(Atr/s−1) | −γ a |
|---|---|---|---|
| F(1) | 281.1 ± 6.6 | 42.7 ± 1.3 | 0.9994 |
| R(3) | 271.7 ± 6.9 | 39.6 ± 1.3 | 0.9993 |
| Heating Condition | Ea,tr /kJ mol−1 | Atr/s−1 | f(αtr) | R2, a |
|---|---|---|---|---|
| Isothermal | 271.7 ± 0.1 | (1.63 ± 0.01) × 1017 | R(2.99 ± 0.01) | >0.9999 |
| Nonisothermal | 312.5 ± 9.1 | (4.24 ± 0.01) × 1021 | SB(0.06 ± 0.01, 0.70 ± 0.01, 0.33 ± 0.01) | >0.9999 |
| i | ci | Ea,i/kJ mol−1 | Ai/s−1 | |||
|---|---|---|---|---|---|---|
| mi | ni | pi | ||||
| 1 | 0.10 ± 0.01 | 114.9 ± 1.6 | (1.47 ± 0.07) × 1016 | 5.84 ± 0.72 | 1.85 ± 0.14 | −5.80 ± 0.67 |
| 2 | 0.77 ± 0.02 | 129.1 ± 1.0 | (8.19 ± 0.40) × 1010 | 9.25 ± 0.76 | 0.73 ± 0.23 | −9.80 ± 0.66 |
| 3 | 0.13 ± 0.01 | 339.1 ± 4.0 | (1.55 ± 0.01) × 1013 | −28.85 ± 2.12 | 8.55 ± 0.90 | 20.71 ± 2.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tone, T.; Koga, N. Interplay between Thermally Induced Aragonite–Calcite Transformation and Multistep Dehydration in a Seawater Spiral Shell (Euplica scripta). Processes 2023, 11, 1650. https://doi.org/10.3390/pr11061650
Tone T, Koga N. Interplay between Thermally Induced Aragonite–Calcite Transformation and Multistep Dehydration in a Seawater Spiral Shell (Euplica scripta). Processes. 2023; 11(6):1650. https://doi.org/10.3390/pr11061650
Chicago/Turabian StyleTone, Taiga, and Nobuyoshi Koga. 2023. "Interplay between Thermally Induced Aragonite–Calcite Transformation and Multistep Dehydration in a Seawater Spiral Shell (Euplica scripta)" Processes 11, no. 6: 1650. https://doi.org/10.3390/pr11061650
APA StyleTone, T., & Koga, N. (2023). Interplay between Thermally Induced Aragonite–Calcite Transformation and Multistep Dehydration in a Seawater Spiral Shell (Euplica scripta). Processes, 11(6), 1650. https://doi.org/10.3390/pr11061650