Using Adsorption Energy Distribution for Parameter Estimation of Competitive Cofactor Coupled Enzyme Reaction
Abstract
:1. Introduction
2. Materials and Methods
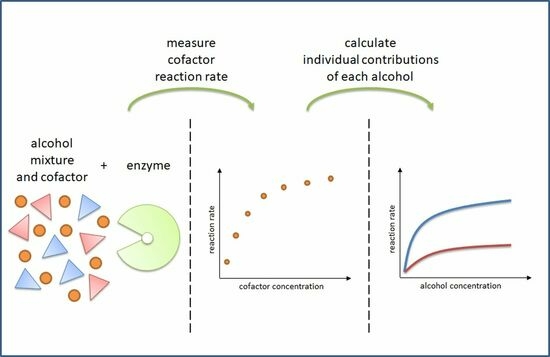
2.1. Adsorption Energy Distribution
2.2. Experimental Desgin
2.3. Data Analysis with Matlab R2022b
3. Results and Discussion
3.1. Single Alcohol Reaction
3.2. Competing Alcohol Reaction
Identification of Substrates
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Erdem, E.; Woodley, J.M. Industrially useful enzymology: Translating biocatalysis from laboratory to process. Chem Catal. 2022, 2, 2499–2505. [Google Scholar] [CrossRef]
- Cavalcante, F.T.T.; Cavalcante, A.L.G.; de Sousa, I.G.; Neto, F.S.; dos Santos, J.C.S. Current Status and Future Perspectives of Supports and Protocols for Enzyme Immobilization. Catalysts 2021, 11, 1222. [Google Scholar] [CrossRef]
- Benvenuto, M.A. Industrial Biotechnology; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Straathof, A.J.J.; Wahl, S.A.; Benjamin, K.R.; Takors, R.; Wierckx, N.; Noorman, H.J. Grand Research Challenges for Sustainable Industrial Biotechnology. Trends Biotechnol. 2019, 37, 1042–1050. [Google Scholar] [CrossRef] [PubMed]
- Chapman, J.; Ismail, A.; Dinu, C. Industrial Applications of Enzymes: Recent Advances, Techniques, and Outlooks. Catalysts 2018, 8, 238. [Google Scholar] [CrossRef]
- Meyer, F.; Gasimov, N.; Bubenheim, P.; Waluga, T. Concept of an Enzymatic Reactive Extraction Centrifuge. Processes 2022, 10, 2137. [Google Scholar] [CrossRef]
- Wenda, S.; Illner, S.; Mell, A.; Kragl, U. Industrial biotechnology—The future of green chemistry? Green Chem. 2011, 13, 3007. [Google Scholar] [CrossRef]
- Lv, L.; Dai, L.; Du, W.; Liu, D. Progress in Enzymatic Biodiesel Production and Commercialization. Processes 2021, 9, 355. [Google Scholar] [CrossRef]
- Woodley, J.M. Biocatalysis for future sustainable manufacturing. Biochem. 2022, 44, 6–8. [Google Scholar] [CrossRef]
- Fernandes, P.; de Carvalho, C.C.C.R. Multi-Enzyme Systems in Flow Chemistry. Processes 2021, 9, 225. [Google Scholar] [CrossRef]
- Johannsen, J.; Meyer, F.; Engelmann, C.; Liese, A.; Fieg, G.; Bubenheim, P.; Waluga, T. Multi-enzyme cascade reaction in a miniplant two-phase-system: Model validation and mathematical optimization. AIChE J. 2021, 67, e17158. [Google Scholar] [CrossRef]
- Woodley, J.M. Accelerating the implementation of biocatalysis in industry. Appl. Microbiol. Biotechnol. 2019, 103, 4733–4739. [Google Scholar] [CrossRef]
- Siedentop, R.; Dziennus, M.; Lütz, S.; Rosenthal, K. Debottlenecking of an In Vitro Enzyme Cascade Using a Combined Model- and Experiment-Based Approach. Chem. Ing. Tech. 2023, 95, 543–548. [Google Scholar] [CrossRef]
- Boodhoo, K.; Flickinger, M.C.; Woodley, J.M.; Emanuelsson, E. Bioprocess intensification: A route to efficient and sustainable biocatalytic transformations for the future. Chem. Eng. Process. Process Intensif. 2022, 172, 108793. [Google Scholar] [CrossRef]
- Zavrel, M.; Kochanowski, K.; Spiess, A.C. Comparison of different approaches and computer programs for progress curve analysis of enzyme kinetics. Eng. Life Sci. 2010, 10, 191–200. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Miguez, F.E. Nonlinear Regression Models and Applications in Agricultural Research. Agron. J. 2015, 107, 786–798. [Google Scholar] [CrossRef]
- Bisswanger, H. Enzyme Kinetics: Principles and Methods, 3rd ed.; Enlarged and Improved Edition; Wiley-VCH: Weinheim, Germany, 2017; ISBN 9783527806461. [Google Scholar]
- Cornish-Bowden, A. Fundamentals of Enzyme Kinetics, 4th ed.; Wiley-VCH: Weinheim, Germany, 2012; ISBN 9783527665488. [Google Scholar]
- Straathof, A. Development of a computer program for analysis of enzyme kinetics by progress curve fitting. J. Mol. Catal. B Enzym. 2001, 11, 991–998. [Google Scholar] [CrossRef]
- Brendel, M.; Bonvin, D.; Marquardt, W. Incremental identification of kinetic models for homogeneous reaction systems. Chem. Eng. Sci. 2006, 61, 5404–5420. [Google Scholar] [CrossRef]
- Michalik, C.; Schmidt, T.; Zavrel, M.; Ansorge-Schumacher, M.; Spiess, A.; Marquardt, W. Application of the incremental identification method to the formate oxidation using formate dehydrogenase. Chem. Eng. Sci. 2007, 62, 5592–5597. [Google Scholar] [CrossRef]
- Buzzi Ferraris, G.; Forzatti, P.; Emig, G.; Hofmann, H. Sequential experimental design for model discrimination in the case of multiple responses. Chem. Eng. Sci. 1984, 39, 81–85. [Google Scholar] [CrossRef]
- Ohs, R.; Leipnitz, M.; Schöpping, M.; Spiess, A.C. Simultaneous identification of reaction and inactivation kinetics of an enzyme-catalyzed carboligation. Biotechnol. Prog. 2018, 34, 1081–1092. [Google Scholar] [CrossRef]
- Michalik, C.; Stuckert, M.; Marquardt, W. Optimal Experimental Design for Discriminating Numerous Model Candidates: The AWDC Criterion. Ind. Eng. Chem. Res. 2010, 49, 913–919. [Google Scholar] [CrossRef]
- Waluga, T.; Klein, M.; Skiborowski, M. On the Use of the Adsorption Energy Distribution for the Analysis of Competing Substrate Kinetics. Ind. Eng. Chem. Res. 2023, 62, 355–364. [Google Scholar] [CrossRef]
- Sanghani, P.C.; Robinson, H.; Bennett-Lovsey, R.; Hurley, T.D.; Bosron, W.F. Structure-function relationships in human Class III alcohol dehydrogenase (formaldehyde dehydrogenase). Chem. Biol. Interact. 2003, 143–144, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Chou, C.-F.; Lai, C.-L.; Chang, Y.-C.; Duester, G.; Yin, S.-J. Kinetic mechanism of human class IV alcohol dehydrogenase functioning as retinol dehydrogenase. J. Biol. Chem. 2002, 277, 25209–25216. [Google Scholar] [CrossRef]
- Mahler, H.R.; Douglas, J. Mechanisms of Enzyme-catalyzed Oxidation-Reduction Reactions. I. An Investigation of the Yeast Alcohol Dehydrogenase Reaction by Means of the Isotope Rate Effect 1,2. J. Am. Chem. Soc. 1957, 79, 1159–1166. [Google Scholar] [CrossRef]
- Dickinson, F.M.; Monger, G.P. A study of the kinetics and mechanism of yeast alcohol dehydrogenase with a variety of substrates. Biochem. J. 1973, 131, 261–270. [Google Scholar] [CrossRef] [PubMed]
- Ganzhorn, A.J.; Green, D.W.; Hershey, A.D.; Gould, R.M.; Plapp, B.V. Kinetic characterization of yeast alcohol dehydrogenases. Amino acid residue 294 and substrate specificity. J. Biol. Chem. 1987, 262, 3754–3761. [Google Scholar] [CrossRef]
- Wratten, C.C.; Cleland, W.W. Kinetic Studies with Liver Alcohol Dehydrogenase*. Biochemistry 1965, 4, 2442–2451. [Google Scholar] [CrossRef]
- Silverstein, E.; Boyer, P.D. Equilibrium Reaction Rates and the Mechanisms of Liver and Yeast Alcohol Dehydrogenase. J. Biol. Chem. 1964, 239, 3908–3914. [Google Scholar] [CrossRef]
- Mazid, M.A.; Laidler, K.J. pH dependence of free and immobilized yeast alcohol dehydrogenase kinetics. Can. J. Biochem. 1982, 60, 100–107. [Google Scholar] [CrossRef] [PubMed]
- Klinman, J.P. The Mechanism of Enzyme-catalyzed Reduced Nicotinamide Adenine Dinucleotide-dependent Reductions. J. Biol. Chem. 1972, 247, 7977–7987. [Google Scholar] [CrossRef] [PubMed]
- Jaroniec, M. Physical adsorption on heterogeneous solids. Adv. Colloid Interface Sci. 1983, 18, 149–225. [Google Scholar] [CrossRef]
- Stanley, B.J.; Guiochon, G. Numerical estimation of adsorption energy distributions from adsorption isotherm data with the expectation-maximization method. J. Phys. Chem. 1993, 97, 8098–8104. [Google Scholar] [CrossRef]
- Stanley, B.J.; Guiochon, G. Importance of the Accuracy of Experimental Data in the Nonlinear Chromatographic Determination of Adsorption Energy Distributions. Langmuir 1994, 10, 4278–4285. [Google Scholar] [CrossRef]
- Nealon, C.M.; Musa, M.M.; Patel, J.M.; Phillips, R.S. Controlling Substrate Specificity and Stereospecificity of Alcohol Dehydrogenases. ACS Catal. 2015, 5, 2100–2114. [Google Scholar] [CrossRef]
- Alcohol-Dehydrogenase aus Saccharomyces Cerevisiae ≥300 units/mg Protein, Lyophilized Powder (Contains Buffer Salts) | Sigma-Aldrich. Available online: https://www.sigmaaldrich.com/DE/de/product/sigma/a7011 (accessed on 21 April 2023).
- Pietruszko, R.; Crawford, K.; Lester, D. Comparison of substrate specificity of alcohol dehydrogenases from human liver, horse liver, and yeast towards saturated and 2-enoic alcohols and aldehydes. Arch. Biochem. Biophys. 1973, 159, 50–60. [Google Scholar] [CrossRef]
- Biegler, L.T.; Damiano, J.J.; Blau, G.E. Nonlinear parameter estimation: A case study comparison. AIChE J. 1986, 32, 29–45. [Google Scholar] [CrossRef]
- Rangheard, M.S.; Langrand, G.; Triantaphylides, C.; Baratti, J. Multi-competitive enzymatic reactions in organic media: A simple test for the determination of lipase fatty acid specificity. Biochim. Biophys. Acta 1989, 1004, 20–28. [Google Scholar] [CrossRef]
- Rangheard, M.-S.; Langrand, G.; Triantaphylides, C.; Baratti, J. Multi-competitive enzymatic reactions in organic media: Application to the determination of lipase alcohol specificity. Enzym. Microb. Technol. 1992, 14, 966–974. [Google Scholar] [CrossRef]
- Bornadel, A.; Akerman, C.O.; Adlercreutz, P.; Hatti-Kaul, R.; Borg, N. Kinetic modeling of lipase-catalyzed esterification reaction between oleic acid and trimethylolpropane: A simplified model for multi-substrate multi-product ping-pong mechanisms. Biotechnol. Prog. 2013, 29, 1422–1429. [Google Scholar] [CrossRef]
- Kuo, Y.-M.; Henry, R.A.; Andrews, A.J. Measuring specificity in multi-substrate/product systems as a tool to investigate selectivity in vivo. Biochim. Biophys. Acta 2016, 1864, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Franceschini, G.; Macchietto, S. Model-based design of experiments for parameter precision: State of the art. Chem. Eng. Sci. 2008, 63, 4846–4872. [Google Scholar] [CrossRef]



| Method | Advantage | Disadvantage |
|---|---|---|
| NLR | Fast calculation (ms–s), established method, diverse (commercial) tools (with GUI) available, many of different solvers available | Initial value necessary, results depends on initial values, local minima can be found, number of competing substrates needs to be known, competing substrates must be analyzed individually, more experimental data necessary |
| AED | No initial values necessary, jet results are independent of initial values. Automatic identification of competing substrates, therefore no need for time-consuming individual analysis, EM algorithm is guaranteed to converge to the global optimum at every iteration for Poisson and Gaussian distribution data, less experimental data necessary | Slow calculation (s–min), complex method, limited solvers available |
| Alcohol | Parameter | AED | NLR | ||
|---|---|---|---|---|---|
| Value | S.E. [%] | Value | S.E. [%] | ||
| 2-butanol | vmax [mol s−1 g−1] | 3.06 × 10−7 | 45.7 | 1.96× 10−7 | 193.05 |
| Km,alc [mM] | 139.50 | 53.8 | 1.30 | 389.65 | |
| Km,NAD [mM] | 1.25 | 76.2 | 3.11 | 280.62 | |
| SSE | 0.65 | 2.66 | |||
| propanol | vmax [mol s−1 g−1] | 8.00 × 10−6 | 3.9 | 1.60 × 10−5 | 95.17 |
| Km,alc [mM] | 11.35 | 14.5 | 1.30 | 192.10 | |
| Km,NAD [mM] | 0.55 | 11.7 | 3.11 | 138.34 | |
| SSE | 0.0056 | 0.60 | |||
| Peak | Parameter | 50/50 | 25/75 | ||
|---|---|---|---|---|---|
| Value | S.E. [%] | Value | S.E. [%] | ||
| 1 | vmax1 [mol s−1 g−1] | 3.35 × 10−6 | 4709 | 3.53 × 10−6 | 929 |
| Km,alc1 [mM] | 28.44 | 5517 | 62.60 | 792 | |
| Km,NAD1 [mM] | 0.75 | 1202 | 0.85 | 298 | |
| 2 | vmax2 [mol s−1 g−1] | 1.54 × 10−6 | 9865 | 2.83 × 10−7 | 11,796 |
| Km,alc2 [mM] | 2.81 | 37,724 | 11.35 | 14,225 | |
| Km,NAD2 [mM] | 1.15 | 5146 | 0.65 | 3641 | |
| SSE | 1.4954 | 0.0650 | |||
| Peak | Parameter | 50/50 | 25/75 | ||
|---|---|---|---|---|---|
| Value | S.E. [%] | Value | S.E. [%] | ||
| 1 | vmax1 [mol s−1 g−1] | 1.41 × 10−5 | 1 × 1011 | 9.39 × 10−6 | 3 × 1010 |
| Km,alc1 [mM] | 1.04 | 4 × 107 | 1.10 | 2 × 107 | |
| Km,NAD1 [mM] | 3.14 | 1 × 107 | 3.18 | 5 × 106 | |
| 2 | vmax2 [mol s−1 g−1] | 0 | ∞ | 0 | ∞ |
| Km,alc2 [mM] | 1.04 | 7 × 1025 | 1.10 | 2 × 1025 | |
| Km,NAD2 [mM] | 3.14 | 2 × 1026 | 3.18 | 1 × 1026 | |
| SSE | 18.7394 | 15.0992 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waluga, T.; Skiborowski, M. Using Adsorption Energy Distribution for Parameter Estimation of Competitive Cofactor Coupled Enzyme Reaction. Processes 2023, 11, 2686. https://doi.org/10.3390/pr11092686
Waluga T, Skiborowski M. Using Adsorption Energy Distribution for Parameter Estimation of Competitive Cofactor Coupled Enzyme Reaction. Processes. 2023; 11(9):2686. https://doi.org/10.3390/pr11092686
Chicago/Turabian StyleWaluga, Thomas, and Mirko Skiborowski. 2023. "Using Adsorption Energy Distribution for Parameter Estimation of Competitive Cofactor Coupled Enzyme Reaction" Processes 11, no. 9: 2686. https://doi.org/10.3390/pr11092686
APA StyleWaluga, T., & Skiborowski, M. (2023). Using Adsorption Energy Distribution for Parameter Estimation of Competitive Cofactor Coupled Enzyme Reaction. Processes, 11(9), 2686. https://doi.org/10.3390/pr11092686