The Material Balance of Complex Separation Flowsheets
Abstract
:1. Introduction
2. Computational Methods
3. Theoretical Analysis
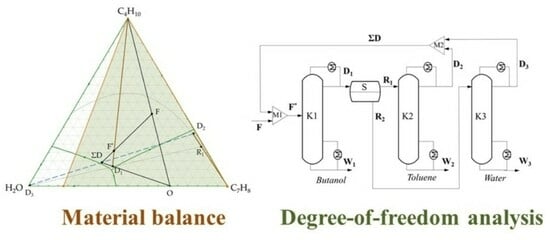
3.1. n-Butanol + Water + Toluene Ternary System
3.2. n-Butanol + Butyl Acetate + Water Ternary System
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sinnott, R.K. Chemical Engineering. In Chemical Engineering Design, 4th ed.; Elsevier: Oxford, UK, 2005; Volume 6, pp. 34–57. [Google Scholar]
- Timofeev, V.S.; Serafimov, L.A.; Tymoshenko, A.V. Principles of the Technology of Basic Organic and Petrochemical Synthesis; Textbook for Universities; Higher School: Moscow, Russia, 2010; pp. 9–13. (In Russian) [Google Scholar]
- Felder, R.M.; Rousseau, R.W. Elementary Principles of Chemical Processes, 6th ed.; Pearson: London, UK, 1995; pp. 250–310. [Google Scholar]
- Chopey, N.P. (Ed.) Handbook of Chemical Engineering Calculations; McGraw-Hill: New York, NY, USA, 1984; pp. 348–360. [Google Scholar]
- Kostikova, N.A.; Glukhan, E.N.; Kazakov, P.V.; Antonova, M.M.; Klimov, D.I. Assessment of resource-saving technologies in low-tonnage chemical industries for compliance with best available technologies principles. Fine Chem. Technol. 2023, 18, 187–218. [Google Scholar] [CrossRef]
- Seidel, T.; Hoffmann, A.; Bortz, M.; Scherrer, A.; Burger, J.; Asprion, N.; Küfer, K.-H.; Hasse, H. A novel approach for infeasible path optimization of distillation-based flowsheets. Chem. Eng. Sci. X 2020, 7, 100063. [Google Scholar] [CrossRef]
- Gerbaud, V.; Rodriguez-Donis, I.; Hegely, L.; Lang, P.; Denes, F.; You, X. Review of Extractive Distillation. Process design, operation optimization and control. Chem. Eng. Res. Des. 2019, 141, 229–271. [Google Scholar] [CrossRef]
- Raeva, V.M.; Stoyakina, I.E. Selecting Extractive Agents on the Basis of Composition-Excess Gibbs Energy Data. Russ. J. Phys. Chem. A 2021, 95, 1779–1790. [Google Scholar] [CrossRef]
- Prayoonyong, P.; Jobson, M. Flowsheet synthesis and complex distillation column design for separating ternary heterogeneous azeotropic mixtures. Chem. Eng. Res. Des. 2011, 89, 1362–1376. [Google Scholar] [CrossRef]
- Petlyuk, F.B.; Danilov, R.Y. Synthesis of separation flowsheets for multicomponent azeotropic mixtures on the basis of the distillation theory. Presynthesis: Prediction of feasible product compositions. Theor. Found. Chem. Eng. 2000, 34, 236–254. [Google Scholar] [CrossRef]
- Serafimov, L.A.; Frolkova, A.K.; Pavlenko, T.G. Determination of conditions for existence of stationary regimes of complexes with recycles for ternary mixture separation. Theor. Found. Chem. Eng. 1992, 26, 281–286. (In Russian) [Google Scholar]
- Frolkova, A.V.; Ablizin, M.A.; Mayevskiy, M.A.; Frolkova, A.K. The multivariate calculation of material balances of flowsheets for separating ternary mixtures of different physical-chemical nature. Fine Chem. Technol. 2016, 11, 47–57. [Google Scholar] [CrossRef]
- Frolkova, A.V.; Frolkova, A.K.; Podtyagina, A.V.; Spiryakova, V.V. Energy savings in flowsheets based on combination in splitting and distillation processes. Theor. Found. Chem. Eng. 2018, 52, 771–778. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Orr, V.; Coates, J. Versatile vapor-liquid equilibrium still. Ind. Eng. Chem. 1960, 52, 27–30. [Google Scholar] [CrossRef]
- Gomis, V.; Font, A.; Saquete, M.D. Homogeneity of the water + ethanol + toluene azeotrope at 101.3 kPa. Fluid Phase Equilib. 2008, 266, 8–13. [Google Scholar] [CrossRef]
- Gorbunov, A.N.; Susarev, M.P.; Balashova, I.M. Liquid-Vapor Equilibrium in the System Isobutyl Acetate-n-Butyl Alcohol-Toluene. Zh. Prikl. Khim. 1968, 41, 312–316. [Google Scholar]
- Gomis, V.; Font, A.; Saquete, M.D.; Garcia-Cano, J. Phase equilibria of the water + 1-butanol + toluene ternary system at 101.3 kPa. Fluid Phase Equilib. 2015, 385, 29–36. [Google Scholar] [CrossRef]
- Wu, Y.-Y.; Pan, D.-T.; Zhu, J.-W.; Chen, K.; Wu, B.; Ji, L. Liquid–liquid equilibria of water + 2,3-butanediol + isobutanol at several temperatures. Fluid Phase Equilib. 2012, 325, 100–104. [Google Scholar] [CrossRef]
- Hirata, M.; Hirose, Y.; Kagaku, K. Vapor-liquid equilibria of ternary system water–acetic acid–n-butyl acetate. Chem. Eng. 1966, 30, 121–127. [Google Scholar] [CrossRef]
- González, E.; Ortega, J. Densities and Isobaric Vapor−Liquid Equilibria for the Mixtures Formed by Four Butyl Esters and 1-Butanol. J. Chem. Eng. Data 1996, 41, 53–58. [Google Scholar] [CrossRef]
- Zhuchkov, V.I.; Nazanskiy, S.L.; Solokhin, A.V.; Frolkova, A.K. Determination of azeotropes in the n-butanol–n-buthylacetate–water system. Chem. Technol. Org. Subst. 2022, 21, 12–19. (In Russian) [Google Scholar]
- Escudero, I.; Cabezas, J.L.; Coca, J. Liquid-Liquid Equilibria for 2,3-Butanediol + Water + 4-(1-Methylpropyl) phenol + Toluene at 25 °C. J. Chem. Eng. Data 1996, 41, 2–5. [Google Scholar] [CrossRef]
- Grande, M.D.C.; Marschoff, C.M. Liquid-Liquid Equilibria for Water + Benzonitrile + Ethyl Acetate or + Butyl Acetate. J. Chem. Eng. Data 2005, 50, 1324–1327. [Google Scholar] [CrossRef]
- Golikova, A.; Shasherina, A.; Anufrikov, Y.; Misikov, G.; Toikka, M.; Zvereva, I.; Toikka, A. Excess enthalpies for binary mixtures of the reactive system acetic acid + n-butanol + n-butyl acetate + water: Brief data review and results at 313.15 k and atmospheric pressure. Int. J. Mol. Sci. 2023, 24, 5137. [Google Scholar] [CrossRef] [PubMed]
- Serafimov, L.A. Thermodynamical and topological analysis of liquid-vapor phase equilibrium diagrams and problems rectification of multicomponent mixtures. Math. Method Contemp. Chem. 1996, 10, 557. [Google Scholar]











| Pure Component/ Azeotrope | x1(2)cal (Mole Frac.) | x1(2)exp (Mole Frac.) | u (Mole Frac.) | ur | Tcal (K) | Texp (K) | u (K) | ur |
|---|---|---|---|---|---|---|---|---|
| B | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 390.90 | 390.80 | 0.1000 | 0.0002 |
| W | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 373.17 | 373.15 | 0.0020 | 0.0001 |
| T | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 383.83 | 383.75 | 0.0800 | 0.0002 |
| BA | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 399.16 | 399.45 | 0.2900 | 0.0007 |
| W + B | 0.7640 | 0.7600 | 0.0040 | 0.0053 | 366.16 | 365.65 | 0.5100 | 0.0014 |
| T + B | 0.6630 | 0.6730 | 0.0100 | 0.0148 | 379.04 | 378.15 | 0.8900 | 0.0024 |
| W + T | 0.5597 | 0.5610 | 0.0013 | 0.0023 | 357.68 | 357.34 | 0.3400 | 0.0009 |
| B + BA | 0.7718 | 0.7780 | 0.0062 | 0.0080 | 390.05 | 389.64 | 0.4100 | 0.0010 |
| W + BA | 0.6982 | 0.7220 | 0.0238 | 0.0329 | 363.36 | 364.12 | 0.7600 | 0.0021 |
| W + T + B | 0.5346 (0.3725) | 0.5320 (0.3880) | 0.0026 (0.0155) | 0.0049 (0.0437) | 356.68 | 356.45 | 0.2300 | 0.0006 |
| BA + W + B | 0.2242 (0.6817) | 0.2240 (0.7034) | 0.0002 (0.0217) | 0.0009 (0.0308) | 362.84 | 363.52 | 0.68 | 0.0019 |
| Binary System | x2′ (cal) (Mole Frac.) | x1″ (cal) (Mole Frac.) | x2′ (exp) (Mole Frac.) | x1″ (exp) (Mole Frac.) | u (x2′) (Mole Frac.) | ur (x2′) | u (x1″) (Mole Frac.) | ur (x1″) |
|---|---|---|---|---|---|---|---|---|
| W + B | 0.4769 | 0.9911 | 0.4900 | 0.9940 | 0.0131 | 0.0267 | 0.0029 | 0.0030 |
| W + T | 0.9999 | 0.9982 | 0.9999 | 0.9985 | 0.0000 | 0.0000 | 0.0003 | 0.0003 |
| W + BA | 0.9249 | 0.9992 | 0.9356 | 0.9990 | 0.0107 | 0.0114 | 0.0002 | 0.0002 |
| Flow | The Amount of Flow, kmol/h | The Amount of Components in Flow, kmol/h | The Flow Composition, Mole Frac. | |
|---|---|---|---|---|
| F* | 141.9 | B | 85.90 | 0.6054 |
| W | 32.59 | 0.2297 | ||
| T | 23.41 | 0.1649 | ||
| F | 100.0 | B | 78.20 | 0.7820 |
| W | 15.00 | 0.1500 | ||
| T | 6.80 | 0.0680 | ||
| D1 | 63.7 | B | 7.70 | 0.1209 |
| W | 32.59 | 0.5116 | ||
| T | 23.41 | 0.3675 | ||
| R1 | 31.5 | B | 7.67 | 0.2434 |
| W | 0.42 | 0.0134 | ||
| T | 23.41 | 0.7432 | ||
| R2 | 32.2 | B | 0.03 | 0.0008 |
| W | 32.17 | 0.9992 | ||
| T | 0.00 | traces | ||
| W1 | 78.2 | B | 78.20 | 1.0000 |
| W | 0.00 | 0.0000 | ||
| T | 0.00 | 0.0000 | ||
| W2 | 6.8 | B | 0.00 | 0.0000 |
| W | 0.00 | 0.0000 | ||
| T | 6.80 | 1.0000 | ||
| W3 | 15.0 | B | 0.00 | 0.0000 |
| W | 15.00 | 1.0000 | ||
| T | 0.00 | 0.0000 | ||
| D2 | 24.7 | B | 7.67 | 0.3100 |
| W | 0.42 | 0.0170 | ||
| T | 16.61 | 0.6730 | ||
| D3 | 17.2 | B | 0.03 | 0.0017 |
| W | 17.17 | 0.9983 | ||
| T | 0.00 | traces | ||
| ΣD | 41.9 | B | 7.70 | 0.1838 |
| W | 17.59 | 0.4198 | ||
| T | 16.61 | 0.3964 | ||
| Flow | The Amount of Flow, kmol/h | The Amount of Components in Flow, kmol/h | The Flow Composition, Mole Frac. | |
|---|---|---|---|---|
| F* | 214.0 | B | 95.76 | 0.4475 |
| W | 76.73 | 0.3585 | ||
| T | 41.51 | 0.1940 | ||
| F | 100.0 | B | 78.20 | 0.7820 |
| W | 15.00 | 0.1500 | ||
| T | 6.80 | 0.0680 | ||
| D1 | 135.8 | B | 17.56 | 0.1293 |
| W | 76.73 | 0.5650 | ||
| T | 41.51 | 0.3057 | ||
| R1 | 60.1 | B | 17.48 | 0.2908 |
| W | 1.11 | 0.0185 | ||
| T | 41.51 | 0.6907 | ||
| R2 | 75.7 | B | 0.08 | 0.0010 |
| W | 75.62 | 0.9990 | ||
| T | 0.00 | traces | ||
| W1 | 78.2 | B | 78.20 | 1.0000 |
| W | 0.00 | 0.0000 | ||
| T | 0.00 | 0.0000 | ||
| W2 | 6.8 | B | 0.00 | 0.0000 |
| W | 0.00 | 0.0000 | ||
| T | 6.80 | 1.0000 | ||
| W3 | 15.0 | B | 0.00 | 0.0000 |
| W | 15.00 | 1.0000 | ||
| T | 0.00 | 0.0000 | ||
| D2 | 53.3 | B | 17.48 | 0.3280 |
| W | 1.11 | 0.0208 | ||
| T | 34.71 | 0.6512 | ||
| D3 | 60.7 | B | 0.08 | 0.0013 |
| W | 60.62 | 0.9987 | ||
| T | 0.00 | traces | ||
| ΣD | 114.0 | B | 17.56 | 0.1540 |
| W | 61.73 | 0.5415 | ||
| T | 34.71 | 0.3045 | ||
| Flow | The Amount of Flow, kmol/h | The Amount of Components in Flow, kmol/h | The Flow Composition, Mole Frac. | |
|---|---|---|---|---|
| F* | 164.2 | B | 95.71 | 0.5829 |
| W | 26.98 | 0.1643 | ||
| T | 41.51 | 0.2528 | ||
| F | 100.0 | B | 78.20 | 0.7820 |
| W | 15.00 | 0.1500 | ||
| T | 6.80 | 0.0680 | ||
| D1 | 86.0 | B | 17.51 | 0.2036 |
| W | 26.98 | 0.3137 | ||
| T | 41.51 | 0.4827 | ||
| R1 | 60.1 | B | 17.48 | 0.2908 |
| W | 1.11 | 0.0185 | ||
| T | 41.51 | 0.6907 | ||
| R2 | 25.9 | B | 0.30 | 0.0010 |
| W | 25.87 | 0.9990 | ||
| T | 0.00 | traces | ||
| W1 | 78.2 | B | 78.20 | 1.0000 |
| W | 0.00 | 0.0000 | ||
| T | 0.00 | 0.0000 | ||
| W2 | 6.8 | B | 0.00 | 0.0000 |
| W | 0.00 | 0.0000 | ||
| T | 6.80 | 1.0000 | ||
| W3 | 15.0 | B | 0.00 | 0.0000 |
| W | 15.00 | 1.0000 | ||
| T | 0.00 | 0.0000 | ||
| D2 | 53.3 | B | 17.48 | 0.3280 |
| W | 1.11 | 0.0208 | ||
| T | 34.71 | 0.6512 | ||
| D3 | 10.9 | B | 0.03 | 0.0028 |
| W | 10.87 | 0.9972 | ||
| T | 0.00 | traces | ||
| ΣD | 64.2 | B | 17.51 | 0.2727 |
| W | 11.98 | 0.1866 | ||
| T | 34.71 | 0.5407 | ||
| Column | Number of Stages/Feed Stage | Reflux Ratio | Number of Stages/Feed Stage | Reflux Ratio | Number of Stages/Feed Stage | Reflux Ratio |
|---|---|---|---|---|---|---|
| Variant I | Variant II | Variant III | ||||
| K1 | 21/13 | 0.738 | 10/2 | 0.001 | 15/7 | 0.79 |
| K2 | 14/4 | 0.500 | 13/3 | 0.550 | 13/3 | 0.554 |
| K3 | 4/2 | 0.0001 | 4/2 | 0.0001 | 4/2 | 0.0001 |
| Variant | I | II | III | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Column (Separator) | K1 | K2 | K3 | K1 | K2 | K3 | K1 | K2 | K3 |
| Tie-line A (R1/R2 = 0.83) | |||||||||
| Di/Wi | 1.21 | 7.80 | 4.71 | 2.42 | 7.89 | 4.71 | 4.54 | 7.90 | 4.70 |
| Tie-line B (R1/R2 = 0.84) | |||||||||
| Di/Wi | 0.79 | 4.87 | 2.71 | 1.51 | 4.80 | 2.69 | 2.96 | 4.82 | 2.71 |
| Column | Number of Stages/Feed Stage | Reflux Ratio | Number of Stages/Feed Stage | Reflux Ratio | Number of Stages/Feed Stage | Reflux Ratio |
|---|---|---|---|---|---|---|
| Variant I | Variant II | Variant III | ||||
| K1 | 46/18 | 4.5 | 48/21 | 3.0 | 48/19 | 2.1 |
| K2 | 50/40 | 3.6 | 40/26 | 2.7 | 43/30 | 2.2 |
| K3 | 4/2 | 0.001 | 4/2 | 0.001 | 4/2 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frolkova, A.; Frolkova, A.; Sibirtsev, M.; Lysenko, K. The Material Balance of Complex Separation Flowsheets. Processes 2024, 12, 821. https://doi.org/10.3390/pr12040821
Frolkova A, Frolkova A, Sibirtsev M, Lysenko K. The Material Balance of Complex Separation Flowsheets. Processes. 2024; 12(4):821. https://doi.org/10.3390/pr12040821
Chicago/Turabian StyleFrolkova, Anastasia, Alla Frolkova, Michael Sibirtsev, and Kirill Lysenko. 2024. "The Material Balance of Complex Separation Flowsheets" Processes 12, no. 4: 821. https://doi.org/10.3390/pr12040821
APA StyleFrolkova, A., Frolkova, A., Sibirtsev, M., & Lysenko, K. (2024). The Material Balance of Complex Separation Flowsheets. Processes, 12(4), 821. https://doi.org/10.3390/pr12040821