A Multicellular Vascular Model of the Renal Myogenic Response
Abstract
:1. Introduction
2. Mathematical Model
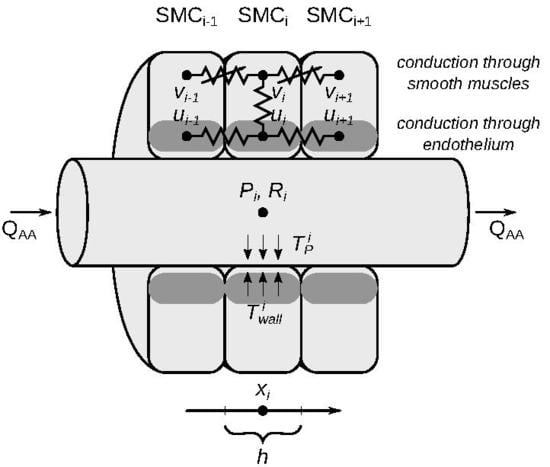
2.1. Model Description
2.1.1. Vascular Blood Flow
2.1.2. Vascular Wall
2.2. Numerical Methods
2.3. Parameter Values
2.3.1. Vascular Geometry and Hemodynamics
2.3.2. Electrophysiology
3. Model Results
3.1. Responses to Steady Perturbations
3.2. Responses to a Step Perturbation
3.3. Responses to Sinusoidal Perturbation
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hall, J.E. Guyton and Hall Textbook of Medical Physiology; Elsevier Health Sciences: New York, NY, USA, 2015. [Google Scholar]
- Holstein-Rathlou, N.H.; Marsh, D.J. Renal blood flow regulation and arterial pressure fluctuations: A case study in nonlinear dynamics. Physiol. Rev. 1994, 74, 637–681. [Google Scholar] [CrossRef] [PubMed]
- Just, A.; Arendshorst, W.J. Dynamics and contribution of mechanisms mediating renal blood flow autoregulation. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2003, 285, R619–R631. [Google Scholar] [CrossRef] [PubMed]
- Cupples, W.A.; Braam, B. Assessment of renal autoregulation. Am. J. Physiol. Ren. Physiol. 2007, 292, F1105–F1123. [Google Scholar] [CrossRef] [PubMed]
- Carlström, M.; Wilcox, C.S.; Arendshorst, W.J. Renal autoregulation in health and disease. Physiol. Rev. 2015, 95, 405–511. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Sgouralis, I.; Moore, L.C.; Layton, H.E.; Layton, A.T. A mathematical model of the myogenic response to systolic pressure in the afferent arteriole. Am. J. Physiol. Ren. Physiol. 2011, 300, F669–F681. [Google Scholar] [CrossRef] [PubMed]
- Sgouralis, I.; Layton, A.T. Theoretical assessment of renal autoregulatory mechanisms. Am. J. Physiol. Ren. Physiol. 2014, 306, F1357–F1371. [Google Scholar] [CrossRef] [PubMed]
- Casellas, D.; Moore, L.C. Autoregulation of intravascular pressure in preglomerular juxtamedullary vessels. Am. J. Physiol. Ren. Physiol. 1993, 264, F315–F321. [Google Scholar] [CrossRef] [PubMed]
- Aukland, K.; Oien, A. Renal autoregulation: models combining tubuloglomerular feedback and myogenic response. Am. J. Physiol. Ren. Physiol. 1987, 252, F768–F783. [Google Scholar] [CrossRef] [PubMed]
- Moore, L.C.; Rich, A.; Casellas, D. Ascending myogenic autoregulation: Interactions between tubuloglomerular feedback and myogenic mechanisms. Bull. Math. Biol. 1994, 56, 391–410. [Google Scholar] [CrossRef] [PubMed]
- Shipley, R.; Study, R. Changes in renal blood flow, extraction of inulin, glomerular filtration rate, tissue pressure and urine flow with acute alterations of renal artery blood pressure. Am. J. Physiol. Leg. Content 1951, 167, 676–688. [Google Scholar] [CrossRef] [PubMed]
- Rothe, C.F.; Nash, F.D.; Thompson, D.E. Patterns in autoregulation of renal blood flow in the dog. Am. J. Physiol. Leg. Content 1971, 220, 1621–1626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arendshorst, W.J. Autoregulation of renal blood flow in spontaneously hypertensive rats. Circ. Res. 1979, 44, 344–349. [Google Scholar] [CrossRef] [PubMed]
- Kirchheim, H.; Ehmke, H.; Hackenthal, E.; Löwe, W.; Persson, P. Autoregulation of renal blood flow, glomerular filtration rate and renin release in conscious dogs. Pflügers Archiv-Eur. J. Physiol. 1987, 410, 441–449. [Google Scholar] [CrossRef]
- Hayashi, K.; Epstein, M.; Loutzenhiser, R.; Forster, H. Impaired myogenic responsiveness of the afferent arteriole in streptozotocin-induced diabetic rats: role of eicosanoid derangements. J. Am. Soc. Nephrol. 1992, 2, 1578–1586. [Google Scholar] [PubMed]
- Van Dokkum, R.P.; Sun, C.W.; Provoost, A.P.; Jacob, H.J.; Roman, R.J. Altered renal hemodynamics and impaired myogenic responses in the fawn-hooded rat. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1999, 276, R855–R863. [Google Scholar] [CrossRef]
- Mitrou, N.; Braam, B.; Cupples, W.A. A gap junction inhibitor, carbenoxolone, induces spatiotemporal dispersion of renal cortical perfusion and impairs autoregulation. Am. J. Physiol. Heart Circ. Physiol. 2016, 311, H582–H591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moss, N.G.; Gentle, T.K.; Arendshorst, W.J. Modulation of the myogenic mechanism: concordant effects of NO synthesis inhibition and O2- dismutation on renal autoregulation in the time and frequency domains. Am. J. Physiol. Ren. Physiol. 2016, 310, F832–F845. [Google Scholar] [CrossRef] [PubMed]
- Oien, A.; Aukland, K. A mathematical analysis of the myogenic hypothesis with special reference to autoregulation of renal blood flow. Circ. Res. 1983, 52, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Loutzenhiser, R.; Bidani, A.; Chilton, L. Renal myogenic response: Kinetic attributes and physiological role. Circ. Res. 2002, 90, 1316–1324. [Google Scholar] [CrossRef] [PubMed]
- Loutzenhiser, R.; Bidani, A.K.; Wang, X. Systolic pressure and the myogenic response of the renal afferent arteriole. Acta Physiol. Scand. 2004, 181, 407–413. [Google Scholar] [CrossRef] [PubMed]
- Marsh, D.J.; Sosnovtseva, O.V.; Chon, K.H.; Holstein-Rathlou, N.H. Nonlinear interactions in renal blood flow regulation. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2005, 288, R1143–R1159. [Google Scholar] [CrossRef] [PubMed]
- Kleinstreuer, N.; David, T.; Plank, M.J.; Endre, Z. Dynamic myogenic autoregulation in the rat kidney: A whole-organ model. Am. J. Physiol. Ren. Physiol. 2008, 294, F1453–F1464. [Google Scholar] [CrossRef] [PubMed]
- Marsh, D.J.; Wexler, A.S.; Brazhe, A.; Postnov, D.E.; Sosnovtseva, O.V.; Holstein-Rathlou, N.H. Multinephron dynamics on the renal vascular network. Am. J. Physiol. Ren. Physiol. 2012, 304, F88–F102. [Google Scholar] [CrossRef] [PubMed]
- Postnov, D.; Postnov, D.; Marsh, D.; Holstein-Rathlou, N.H.; Sosnovtseva, O. Dynamics of nephron-vascular network. Bull. Math. Biol. 2012, 74, 2820–2841. [Google Scholar] [CrossRef] [PubMed]
- Sgouralis, I.; Maroulas, V.; Layton, A.T. Transfer Function Analysis of Dynamic Blood Flow Control in the Rat Kidney. Bull. Math. Biol. 2016, 78, 923–960. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sgouralis, I.; Layton, A.T. Conduction of feedback-mediated signal in a computational model of coupled nephrons. Math. Med. Biol. 2015, 33, 87–106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Postnov, D.D.; Marsh, D.J.; Postnov, D.E.; Braunstein, T.H.; Holstein-Rathlou, N.H.; Martens, E.A.; Sosnovtseva, O. Modeling of kidney hemodynamics: Probability-based topology of an arterial network. PLoS Comput. Biol. 2016, 12, e1004922. [Google Scholar] [CrossRef] [PubMed]
- Edwards, A.; Layton, A. Calcium dynamics underlying the afferent arteriole myogenic response. Am. J. Physiol. Ren. Physiol. 2014, 306, F34–F48. [Google Scholar] [CrossRef] [PubMed]
- Ciocanel, M.V.; Stepien, T.L.; Edwards, A.; Layton, A.T. Modeling autoregulation of the afferent arteriole of the rat kidney. In Women in Mathematical Biology; Springer: Berlin, Germany, 2017; pp. 75–100. [Google Scholar]
- Gui, P.; Chao, J.T.; Wu, X.; Yang, Y.; Davis, G.E.; Davis, M.J. Coordinated regulation of vascular Ca2+ and K+ channels by integrin signaling. In Integrins and Ion Channels; Springer: Berlin, Germany, 2010; pp. 69–79. [Google Scholar]
- Pozzi, A.; Zent, R. Integrins in kidney disease. J. Am. Soc. Nephrol. 2013, 24, 1034–1039. [Google Scholar] [CrossRef] [PubMed]
- Hamm, L.L.; Feng, Z.; Hering-Smith, K.S. Regulation of sodium transport by ENaC in the kidney. Curr. Opin. Nephrol. Hypertens. 2010, 19, 98–105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhalla, V.; Hallows, K.R. Mechanisms of ENaC regulation and clinical implications. J. Am. Soc. Nephrol. 2008, 19, 1845–1854. [Google Scholar] [CrossRef] [PubMed]
- Arendshorst, W.J.; Brännström, K.; Ruan, X. Actions of angiotensin II on the renal microvasculature. J. Am. Soc. Nephrol. 1999, 10, S149–S161. [Google Scholar] [PubMed]
- Yang, R.; Smolders, I.; Dupont, A.G. Blood pressure and renal hemodynamic effects of angiotensin fragments. Hypertens. Res. 2011, 34, 674–683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giani, J.F.; Janjulia, T.; Taylor, B.; Bernstein, E.A.; Shah, K.; Shen, X.Z.; McDonough, A.A.; Bernstein, K.E.; Gonzalez-Villalobos, R.A. Renal generation of angiotensin II and the pathogenesis of hypertension. Curr. Hypertens. Rep. 2014, 16, 477. [Google Scholar] [CrossRef] [PubMed]
- Sparks, M.A.; Crowley, S.D.; Gurley, S.B.; Mirotsou, M.; Coffman, T.M. Classical Renin-Angiotensin System in Kidney Physiology. Compr. Physiol. 2014, 4, 1201–1228. [Google Scholar] [PubMed] [Green Version]
- Majid, D.S.; Navar, L.G. Nitric oxide in the control of renal hemodynamics and excretory function. Am. J. Hypertens. 2001, 14, 74S–82S. [Google Scholar] [CrossRef]
- Mount, P.; Power, D.A. Nitric oxide in the kidney: Functions and regulation of synthesis. Acta Physiol. 2006, 187, 433–446. [Google Scholar] [CrossRef] [PubMed]
- Barber, J.D.; Moss, N.G. Reduced renal perfusion pressure causes prostaglandin-dependent excitation of R2 chemoreceptors in rats. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1990, 259, R1243–R1249. [Google Scholar] [CrossRef] [PubMed]
- Moss, N.G.; Vogel, P.A.; Kopple, T.E.; Arendshorst, W.J. Thromboxane-induced renal vasoconstriction is mediated by the ADP-ribosyl cyclase CD38 and superoxide anion. Am. J. Physiol. Ren. Physiol. 2013, 305, F830–F838. [Google Scholar] [CrossRef] [PubMed]
- Moss, N.G.; Kopple, T.E.; Arendshorst, W.J. Renal vasoconstriction by vasopressin V1a receptors is modulated by nitric oxide, prostanoids, and superoxide but not the ADP ribosyl cyclase CD38. Am. J. Physiol. Ren. Physiol. 2014, 306, F1143–F1154. [Google Scholar] [CrossRef] [PubMed]
- Vogel, P.A.; Yang, X.; Moss, N.G.; Arendshorst, W.J. Superoxide Enhances Ca2+ Entry Through L-Type Channels in the Renal Afferent ArterioleNovelty and Significance. Hypertension 2015, 66, 374–381. [Google Scholar] [CrossRef] [PubMed]
- Loutzenhiser, R.; Griffin, K.; Williamson, G.; Bidani, A. Renal autoregulation: New perspectives regarding the protective and regulatory roles of the underlying mechanisms. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2006, 290, R1153–R1167. [Google Scholar] [CrossRef] [PubMed]
- Inscho, E.W. Mysteries of renal autoregulation. Hypertension 2009, 53, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Montanari, A.; Pelà, G.; Musiari, L.; Crocamo, A.; Boeti, L.; Cabassi, A.; Biggi, A.; Cherney, D.Z. Nitric oxide-angiotensin II interactions and renal hemodynamic function in patients with uncomplicated type 1 diabetes. Am. J. Physiol. Ren. Physiol. 2013, 305, F42–F51. [Google Scholar] [CrossRef] [PubMed]
- Mitrou, N.; Morrison, S.; Mousavi, P.; Braam, B.; Cupples, W.A. Transient impairment of dynamic renal autoregulation in early diabetes mellitus in rats. Ame. J. Physiol. Regul. Integr. Comp. Physiol. 2015, 309, R892–R901. [Google Scholar] [CrossRef] [PubMed]
- Griffin, K.A. Hypertensive kidney injury and the progression of chronic kidney disease. Hypertension 2017, 70, 687–694. [Google Scholar] [CrossRef] [PubMed]
- Bidani, A.K.; Griffin, K.A.; Epstein, M. Hypertension and chronic kidney disease progression: Why the suboptimal outcomes? Am. J. Med. 2012, 125, 1057–1062. [Google Scholar] [CrossRef] [PubMed]
- Moore, L.C.; Casellas, D. Tubuloglomerular feedback dependence of autoregulation in rat juxtamedullary afferent arterioles. Kidney Int. 1990, 37, 1402–1408. [Google Scholar] [CrossRef] [PubMed]
- Nordsletten, D.A.; Blackett, S.; Bentley, M.D.; Ritman, E.L.; Smith, N.P. Structural morphology of renal vasculature. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H296–H309. [Google Scholar] [CrossRef] [PubMed]
- Casellas, D.; Carmines, P.K. Control of the renal microcirculation: Cellular and integrative perspectives. Curr. Opin. Nephrol. Hypertens. 1996, 5, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Steinhausen, M.; Endlich, K.; Nobiling, R.; Parekh, N.; Schütt, F. Electrically induced vasomotor responses and their propagation in rat renal vessels in vivo. J. Physiol. 1997, 505, 493–501. [Google Scholar] [CrossRef] [PubMed]
- Sgouralis, I.; Layton, A. Autoregulation and conduction of vasomotor responses in a mathematical model of the rat afferent arteriole. Am. J. Physiol. Ren. Physiol. 2012, 303, F229–F239. [Google Scholar] [CrossRef] [PubMed]
- Sgouralis, I.; Layton, A.T. Mathematical modeling of renal hemodynamics in physiology and pathophysiology. Math. Biosci. 2015, 264, 8–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pries, A.; Secomb, T.; Gessner, T.; Sperandio, M.; Gross, J.; Gaehtgens, P. Resistance to blood flow in microvessels in vivo. Circ. Res. 1994, 75, 904–915. [Google Scholar] [CrossRef] [PubMed]
- Brenner, B.M.; Troy, J.L.; Daugharty, T.M. Pressures in cortical structures of the rat kidney. Am. J. Physiol. 1972, 222, 246–251. [Google Scholar] [CrossRef] [PubMed]
- Leyssac, P.P. Further studies on oscillating tubulo-glomerular feedback responses in the rat kidney. Acta Physiol. Scand. 1986, 126, 271–277. [Google Scholar] [CrossRef] [PubMed]
- Sgouralis, I.; Layton, A.T. Control and modulation of fluid flow in the rat kidney. Bull. Math. Biol. 2013, 75, 2551–2574. [Google Scholar] [CrossRef] [PubMed]
- Brink, P.R. Gap junctions in vascular smooth muscle. Acta Physiol. Scand. 1998, 164, 349–356. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.J.; Hill, M.A. Signaling mechanisms underlying the vascular myogenic response. Physiol. Rev. 1999, 79, 387–423. [Google Scholar] [CrossRef] [PubMed]
- Kapela, A.; Nagaraja, S.; Tsoukias, N.M. A mathematical model of vasoreactivity in rat mesenteric arterioles. II. Conducted vasoreactivity. Am. J. Physiol. Heart Circ. Physiol. 2009, 298, H52–H65. [Google Scholar] [CrossRef] [PubMed]
- Tran, C.H.T.; Vigmond, E.J.; Goldman, D.; Plane, F.; Welsh, D.G. Electrical communication in branching arterial networks. Am. J. Physiol. Heart Circ. Physiol. 2012, 303, H680–H692. [Google Scholar] [CrossRef] [PubMed]
- Diep, H.K.; Vigmond, E.J.; Segal, S.S.; Welsh, D.G. Defining electrical communication in skeletal muscle resistance arteries: A computational approach. J. Physiol. 2005, 568, 267–281. [Google Scholar] [CrossRef] [PubMed]
- Hald, B.O. A generative modeling approach to connectivity? Electrical conduction in vascular networks. J. Theor. Biol. 2016, 399, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Brenan, K.E.; Campbell, S.L.; Petzold, L.R. Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996; Volume 14. [Google Scholar]
- Chilton, L.; Loutzenhiser, K.; Morales, E.; Breaks, J.; Kargacin, G.J.; Loutzenhiser, R. Inward rectifier K+ currents and Kir2.1 expression in renal afferent and efferent arterioles. J. Am. Soc. Nephrol. 2008, 19, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Loutzenhiser, K.; Loutzenhiser, R. Angiotensin II-induced Ca2+ influx in renal afferent and efferent arterioles: Differing roles of voltage-gated and store-operated Ca2+ entry. Circ. Res. 2000, 87, 551–557. [Google Scholar] [CrossRef] [PubMed]
- Casellas, D.; Moore, L.C. Autoregulation and tubuloglomerular feedback in juxtamedullary glomerular arterioles. Am. J. Physiol. 1990, 258, F660–F669. [Google Scholar] [CrossRef] [PubMed]
- Thomson, S.C.; Blantz, R.C. Biophysics of glomerular filtration. Compr. Physiol. 2012, 2, 1671–1699. [Google Scholar] [PubMed]
- Loutzenhiser, R.; Chilton, L.; Trottier, G. Membrane potential measurements in renal afferent and efferent arterioles: Actions of angiotensin II. Am. J. Physiol. Ren. Physiol. 1997, 273, F307–F314. [Google Scholar] [CrossRef] [PubMed]
- Bidani, A.K.; Hacioglu, R.; Abu-Amarah, I.; Williamson, G.A.; Loutzenhiser, R.; Griffin, K.A. “Step” vs. “dynamic” autoregulation: Implications for susceptibility to hypertensive injury. Am. J. Physiol. Ren. Physiol. 2003, 285, F113–F120. [Google Scholar] [CrossRef] [PubMed]
- Carlson, B.E.; Arciero, J.C.; Secomb, T.W. Theoretical model of blood flow autoregulation: Roles of myogenic, shear-dependent, and metabolic responses. Am. J. Physiol. Heart Circ. Physiol. 2008, 295, H1572–H1579. [Google Scholar] [CrossRef] [PubMed]
- Arciero, J.; Secomb, T. Spontaneous oscillations in a model for active control of microvessel diameters. Math. Med. Biol. 2010, 29, 163–180. [Google Scholar] [CrossRef] [PubMed]
- Versypt, A.N.F.; Makrides, E.; Arciero, J.C.; Ellwein, L.; Layton, A.T. Bifurcation study of blood flow control in the kidney. Math. Biosci. 2015, 263, 169–179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Layton, A.; Vallon, V.; Edwards, A. Modeling oxygen consumption in the proximal tubule: Effects of NHE and SGLT2 inhibition. Am. J. Physiol. Ren. Physiol. 2015, 308, F1343–F1357. [Google Scholar] [CrossRef] [PubMed]
- Layton, A.; Vallon, V.; Edwards, A. Predicted Consequences of diabetes and SGLT inhibition on transport and oxygen consumption along a rat nephron. Am. J. Physiol. Ren. Physiol. 2016, 310, F1269–F1283. [Google Scholar] [CrossRef] [PubMed]
- Layton, A.; Vallon, V.; Edwards, A. A computational model for simulating solute transport and oxygen consumption along the nephron. Am. J. Physiol. Ren. Physiol. 2016, 311, F1378–F1390. [Google Scholar] [CrossRef] [PubMed]
- Layton, A.; Laghmani, K.; Vallon, V.; Edwards, A. Solute transport and oxygen consumption along the nephrons: Effects of Na+ transport inhibitors. Am. J. Physiol. Ren. Physiol. 2016, 311, F1217–F1229. [Google Scholar] [CrossRef] [PubMed]
- Layton, A.T.; Edwards, A.; Vallon, V. Adaptive changes in GFR, tubular morphology, and transport in subtotal nephrectomized kidneys: Modeling and analysis. Am. J. Physiol. Ren. Physiol. 2017, 313, F199–F209. [Google Scholar] [CrossRef] [PubMed]
- Layton, A. Feedback-mediated dynamics in a model of a compliant thick ascending limb. Math. Biosci. 2010, 228, 185–194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Layton, A.; Moore, L.; Layton, H. Multistable dynamics mediated by tubuloglomerular feedback in a model of coupled nephrons. Bull. Math. Biol. 2009, 71, 515–555. [Google Scholar] [CrossRef] [PubMed]
- Ryu, H.; Layton, A. Effect of tubular inhomogeneities on feedback-mediated dynamics of a model of a thick ascending limb. Med. Math. Biol. 2012, 30, 191–212. [Google Scholar] [CrossRef] [PubMed] [Green Version]











| Description | Parameter | Value | Units | Reference |
|---|---|---|---|---|
| Reference afferent arteriole inflow pressure | 100 | mmHg | [55,60] | |
| Reference afferent arteriole outflow pressure | 50 | mmHg | [55,60] | |
| Reference afferent arteriole radius | 10 | m | [29,60] | |
| Reference afferent arteriole flow | 300 | nL/min | [55,60] | |
| Reference glomerular filtration rate | 30 | nL/min | [7,60] | |
| Pressure in renal vein | 4 | mmHg | [7] | |
| Axial length of smooth muscle cell | h | 3 | m | [69] |
| Number of smooth muscle cells | 20 | - | present study | |
| Afferent arteriole length | 60 | m | [69] | |
| Efferent arteriole length | 60 | m | present study | |
| Efferent arteriole radius | 11 | m | [71] | |
| Filtration fraction | 0.1 | - | [72] | |
| Blood viscosity | 6.68 | mmHg ·s | present study | |
| Muscle contraction time constant | 1.71 | s | [29,30] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciocanel, M.-V.; Stepien, T.L.; Sgouralis, I.; Layton, A.T. A Multicellular Vascular Model of the Renal Myogenic Response. Processes 2018, 6, 89. https://doi.org/10.3390/pr6070089
Ciocanel M-V, Stepien TL, Sgouralis I, Layton AT. A Multicellular Vascular Model of the Renal Myogenic Response. Processes. 2018; 6(7):89. https://doi.org/10.3390/pr6070089
Chicago/Turabian StyleCiocanel, Maria-Veronica, Tracy L. Stepien, Ioannis Sgouralis, and Anita T. Layton. 2018. "A Multicellular Vascular Model of the Renal Myogenic Response" Processes 6, no. 7: 89. https://doi.org/10.3390/pr6070089
APA StyleCiocanel, M. -V., Stepien, T. L., Sgouralis, I., & Layton, A. T. (2018). A Multicellular Vascular Model of the Renal Myogenic Response. Processes, 6(7), 89. https://doi.org/10.3390/pr6070089