Sustainable Synthesis Processes for Carbon Dots through Response Surface Methodology and Artificial Neural Network
Abstract
:1. Introduction
2. Mathematical Models and Analytical Methods
2.1. Response Surface Method and Mathematical Model
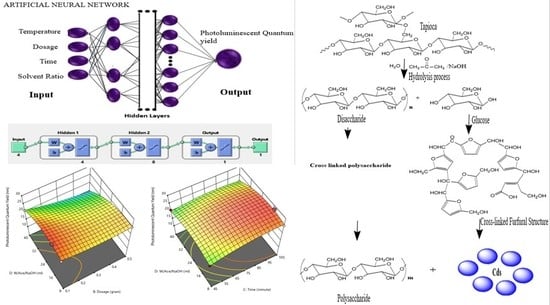
2.2. Artificial Neural Network Mathematical Model and Method
2.3. Synthesis of Carbon Dots (CDs)
3. Result and Discussion
3.1. Response Surface Methodology
- A = temperature, B = dosages, C = time, D = solvent (H2O/C3H6O/NaOH)
- Now, let;
- A = X1, B = X2, C = X3, D = X4 (refer to RSM Table 2)
- i
- Final equation in terms of coded (predicted) factors (full model): Also see Table 3 below for R2 values and lack of fit for the polynomial regression equation.Photoluminescent quantum yield (Response) = 23.63 − 0.1732 X1 + 0.03498 X2 +
0.1905 X3 − 0.0802 X4 − 2.38 X1 X2 + 1.61 X1 X3 − 2.68 X1 X4 + 0.1894 X2 X3 − 1.30 X2 X4 −
0.9353 X3 X4 + 0.2905 X21 + 1.07 X22 − 1.38 X23 − 3.36 X24. - ii
- Final equation in terms of actual factors (full model): Also see Table 4 below for R2 values and lack of fit for the polynomial regression equation.Photoluminescent quantum yield (Response) = −3.3822 + 0.03866 X1 + 22.7576 X2 +
0.1385 X3 + 1.3133 X4 − 0.2379 X1 X2 + 0.0010 X1 X3 − 0.0033 X1 X4 + 0.0315 X2 X3 −
0.4069 X2 X4 − 0.0019 X3 X4 + 0.0001 X21 + 26.8733 X22 − 0.0015 X23 − 0.0131 X24.
Analysis of Variance and Model Statistical Report
- i
- A significant model: Large F-value with p < 0.05.
- ii
- Insignificant lack-of-fit: F-value with p > 0.10.
- iii
3.2. Photoluminescent Quantum Yield
3.3. Evaluation Performance between Artificial Neural Network (ANN) and Response Surface Methodology (RSM) on the Yield of Photoluminescent Quantum Yield
3.4. Characterization and Properties of Carbon Dots
3.4.1. Atomic Force Microscopy (AFM) and High Resolution Transmission Electron Microscopy (HrTEM) of Carbon Dots (CDs)
3.4.2. Field Emission Scanning Electron Microscopy (FESEM) and EDx of Tapioca-Derived Carbon Dots
3.4.3. Properties of Carbon Dots (CDs)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Sheng, Z.; Han, H.; Zou, M.; Li, C. Facile synthesis of fluorescent carbon dots using watermelon peel as a carbon source. Mater. Lett. 2012, 66, 222–224. [Google Scholar] [CrossRef]
- Das, R.; Bandyopadhyay, R.; Pramanik, P. Carbon quantum dots from natural resource: A review. Mater. Today Chem. 2018, 8, 96–109. [Google Scholar] [CrossRef]
- Witek-Krowiak, A.; Chojnacka, K.; Podstawczyk, D.; Dawiec, A.; Pokomeda, K. Application of response surface methodology and artificial neural network methods in modelling and optimization of biosorption process. Bioresour. Technol. 2014, 160, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Nwobi-Okoye, C.C.; Ochieze, B.Q. Age hardening process modeling and optimization of aluminum alloy A356/Cow horn particulate composite for brake drum application using RSM, ANN and simulated annealing. Def. Technol. 2018, 14, 336–345. [Google Scholar] [CrossRef]
- Huang, D.; Zhao, W.; Tang, Y.; Huang, S.; Cao, W. Matching algorithm of missile tail flame based on back-propagation neural network. In Proceedings of the Fourth Seminar on Novel Optoelectronic Detection Technology and Application, Nanjing, China, 24–26 October 2017; p. 1069702. [Google Scholar]
- Lee, J.H.; Delbruck, T.; Pfeiffer, M. Training Deep Spiking Neural Networks Using Backpropagation. Front. Mol. Neurosci. 2016, 10, 508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whittington, J.C.R.; Bogacz, R. An Approximation of the Error Backpropagation Algorithm in a Predictive Coding Network with Local Hebbian Synaptic Plasticity. Neural Comput. 2017, 29, 1229–1262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wisesty, U.N.; Warastri, R.S.; Puspitasari, S.Y. Leukemia and colon tumor detection based on microarray data classification using momentum backpropagation and genetic algorithm as a feature selection method. J. Phys. Conf. Ser. 2018, 971, 012018. [Google Scholar] [CrossRef]
- Chamoli, S. ANN and RSM approach for modeling and optimization of designing parameters for a V down perforated baffle roughened rectangular channel. Alex. Eng. J. 2015, 54, 429–446. [Google Scholar] [CrossRef] [Green Version]
- Baş, D.; Boyacı, I.H.; Boyaci, I.H. Modeling and optimization II: Comparison of estimation capabilities of response surface methodology with artificial neural networks in a biochemical reaction. J. Food Eng. 2007, 78, 846–854. [Google Scholar] [CrossRef]
- Nazari, A.; Riahi, S. Prediction split tensile strength and water permeability of high strength concrete containing TiO2 nanoparticles by artificial neural network and genetic programming. Compos. Part B Eng. 2011, 42, 473–488. [Google Scholar] [CrossRef]
- Nazari, A.; Riahi, S. Artificial neural networks to prediction total specific pore volume of geopolymers produced from waste ashes. Neural Comput. Appl. 2013, 22, 719–729. [Google Scholar] [CrossRef]
- Arumugam, N.; Kim, J. Synthesis of carbon quantum dots from Broccoli and their ability to detect silver ions. Mater. Lett. 2018, 219, 37–40. [Google Scholar] [CrossRef]
- Diao, H.; Li, T.; Zhang, R.; Kang, Y.; Liu, W.; Cui, Y.; Wei, S.; Wang, N.; Li, L.; Wang, H.; et al. Facile and green synthesis of fluorescent carbon dots with tunable emission for sensors and cells imaging. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 200, 226–234. [Google Scholar] [CrossRef] [PubMed]
- Shahla, A.F.; Masoud, S.N.; Davood, G. Hydrothermal green synthesis of magnetic Fe3O4-carbon dots by lemon and grape fruit extracts and as a photoluminescence sensor for detecting of E. coli bacteria. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 203, 481–493. [Google Scholar]
- Fermoso, J.; Gil, M.V.; Arias, B.; Plaza, M.; Pevida, C.; Pis, J.; Rubiera, F. Application of response surface methodology to assess the combined effect of operating variables on high-pressure coal gasification for H2-rich gas production. Int. J. Hydrog. Energy 2010, 35, 1191–1204. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.V.; Yunus, R.; Juan, J.C.; Taufiq-Yap, Y. Process optimization design for jatropha-based biodiesel production using response surface methodology. Fuel Process. Technol. 2011, 92, 2420–2428. [Google Scholar] [CrossRef] [Green Version]
- Kefasa, H.M.; Robiah, Y.; Umer, R.; Yun, T.Y. Modified sulfonation method for converting carbonized glucose into solid acid catalyst for the esterification of palm fatty acid distillate. Fuel 2018, 229, 68–78. [Google Scholar] [CrossRef]
- Rashid, U.; Anwar, F.; Ashraf, M.; Saleem, M.; Yusup, S. Application of response surface methodology for optimizing transesterification of Moringa oliefera oil: Biodiesel production. Energy Convers Manag. 2011, 52, 3034–3042. [Google Scholar] [CrossRef]
- Joglekar, A.; May, A. Product excellence through design of experiments. Cereal Foods World 1987, 32, 857–868. [Google Scholar]
- Betiku, E.; Okunsolawo, S.S.; Ajala, S.O.; Odedele, O.S. Performance evaluation of artificial neural network coupled with generic algorithm and response surface methodology in modeling and optimization of biodiesel production process parameters from shea tree (Vitellaria paradoxa) nut butter. Renew. Energy 2015, 76, 408–417. [Google Scholar] [CrossRef]
- Da Silva Souza, D.R.; Larissa, D.C.; Joao, P.M.; Fabiano, V.P. Luminescent carbon dots obtained from cellulose. Mater. Chem. Phys. 2018, 203, 148–155. [Google Scholar] [CrossRef]
- Horiba Scientific. A Guide to Recording Fluorescence Quantum Yield; Middlesex HA7 IBQ; Horiba UK Limited: Northampton, UK, 2018. [Google Scholar]
- Ashby, S.P.; Thomas, J.A.; Coxon, P.R.; Bilton, M.; Brydson, R.; Pennycook, T.J.; Chao, Y. The effect of alkyl chain length on the level of capping of silicon nanoparticles produced by a one-pot synthesis route based on the chemical reduction of micelle. J. Nanoparticle Res. 2013, 15, 1425–1428. [Google Scholar] [CrossRef]
- Sahu, S.; Behera, B.; Maiti, K.; Mohapatra, S. Simple one-step synthesis of highly luminescent carbon dots from orange juice: Application as excellent bioimaging agents. Chem. Commun. 2012, 48, 8835–8837. [Google Scholar] [CrossRef] [PubMed]
- Jhonsi, M.A.; Thulasi, S. A novel fluorescent carbon dots derived from tamarind. Chem. Phys. Lett. 2016, 661, 179–184. [Google Scholar] [CrossRef]
- Yadav, A.M.; Chaurasia, R.C.; Suresh, N.; Gajbhiye, P. Application of artificial neural networks and response surface methodology approaches for the prediction of oil agglomeration process. Fuel 2018, 220, 826–836. [Google Scholar] [CrossRef]
- Ahmad, H.; Ali, A.N.; Ahmad, J.J.; Reza, K.J.; Mansour, B.; Hasan, B.; Fardin, G.P. Application of response surface methodology and artificial neuralnetwork modeling to assess non-thermal plasma efficiency insimultaneous removal of BTEX from waste gases: Effect of operatingparameters and prediction performance. Process Saf. Environ. Prot. 2018, 119, 261–270. [Google Scholar]
- Shailendra, S.S.; Shraddha, S.; Rathindra, M.B. Preparation of Drug Eluting Natural Composite Scaffold Using Response Surface Methodology and Artificial Neural Network Approach. Tissue Eng. Regen. Med. 2018, 15, 1–13. [Google Scholar]
- Vatankhah, E.; Semnani, D.; Prabhakaran, M.P.; Tadayon, M.; Razavi, S.; Ramakrishna, S. Artificial neural network for modeling the elastic modulus of electrospun polycaprolactone/gelatin scaffolds. Acta Biomater. 2014, 10, 709–721. [Google Scholar] [CrossRef]
- Mukherjee, I.; Routroy, S. Comparing the performance of neural networks developed by using Levenberg–Marquardt and Quasi-Newton with the gradient descent algorithm for modelling a multiple response grinding process. Expert Syst. Appl. 2012, 39, 2397–2407. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Yu, H. Improved Computation for Levenberg–Marquardt Training. IEEE Trans. Neural Netw. 2010, 21, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Varol, T.; Çanakçi, A.; Ozsahin, S. Prediction of effect of reinforcement content, flake size and flake time on the density and hardness of flake AA2024-SiC nanocomposites using neural networks. J. Alloy. Compd. 2018, 739, 1005–1014. [Google Scholar] [CrossRef]
- Saud, P.S.; Pant, B.; Alam, A.-M.; Ghouri, Z.K.; Park, M.; Kim, H.-Y. Carbon quantum dots anchored TiO2 nanofibers: Effective photocatalyst for waste water treatment. Ceram. Int. 2015, 41, 11953–11959. [Google Scholar] [CrossRef]
- Venkatesham, T.; Tanner, A.N.; Denis, O.D.; Ümit, Ö.; Indika, U.A. Ge1−xSnx alloy quantum dots with composition- tunable energy gaps and near-infrared photoluminescence. Nanoscale 2018, 10, 20296–20306. [Google Scholar]
- Siddique, A.B.; Pramanick, A.K.; Chatterjee, S.; Ray, M. Amorphous Carbon Dots and their Remarkable Ability to Detect 2,4,6-Trinitrophenol. Sci. Rep. 2018, 8, 9770. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Li, L.; Chen, C.; Cui, F. Green synthesis of nitrogen-doped carbon dots from ginkgo fruits and the application in cell imaging. Inorg. Chem. Commun. 2017, 86, 227–231. [Google Scholar] [CrossRef]
- Zhao, C.; Jiao, Y.; Hu, F.; Yang, Y. Green synthesis of carbon dots from pork and application as nanosensors for uric acid detection. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 190, 360–367. [Google Scholar] [CrossRef] [PubMed]
- Barman, M.K.; Patra, A. Current status and prospects on chemical structure driven photoluminescence behaviour of carbon dots. J. Photochem. Photobiol. C Photochem. Rev. 2018, 37, 1–22. [Google Scholar] [CrossRef]
- Wanekaya, A.K. Applications of nanoscale carbon-based materials in heavy metal sensing and detection. Analyst 2011, 136, 4383–4391. [Google Scholar] [CrossRef]
- Liu, H.; Ye, T.; Mao, C. Fluorescent Carbon Nanoparticles Derived from Candle Soot. Angew. Chem. Int. Ed. 2007, 46, 6473–6475. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Z.; Zhang, W.; Wang, W.; Chang, J.; Kai, J. Fluorescent carbon dots as nanoprobe for determination of lidocaine hydrochloride. Sens. Actuators B Chem. 2018, 262, 928–937. [Google Scholar] [CrossRef]










| Factor | Name | Units | Low Actual | High Actual | Low Coded | High Coded | Mean | Std. Dev. |
|---|---|---|---|---|---|---|---|---|
| A (X1) | Temp | °C | 75.00 | 175.00 | −1.000 | 1.000 | 125.0 | 40.825 |
| B (X2) | Dosage | g | 0.100 | 0.50 | −1.000 | 1.000 | 0.30 | 0.163 |
| C (X3) | Time | min | 45.00 | 105.00 | −1.000 | 1.000 | 75.00 | 24.495 |
| D (X4) | W/Ace/NaOH | mL | 8.00 | 40.00 | −1.000 | 1.000 | 24.00 | 13.064 |
| Std Order | Factor-A Temperature (°C) | Factor-B Dossage (gram) | Factor-C Time (min) | Factor-D Solvent (mL) (H2O/C3H6O/NaOH) | Exp. Actual Value (PLQY) | Pred. Value | Res. Value |
|---|---|---|---|---|---|---|---|
| 1 | 75 | 0.10 | 45 | 8.00 | 14.67 | 14.41 | 0.26 |
| 2 | 175 | 0.10 | 45 | 8.00 | 21.05 | 20.89 | 0.15 |
| 3 | 75 | 0.50 | 45 | 8.00 | 22.80 | 22.35 | 0.45 |
| 4 | 175 | 0.50 | 45 | 8.00 | 19.96 | 19.13 | 0.83 |
| 5 | 75 | 0.10 | 105 | 8.00 | 14.00 | 13.01 | 0.99 |
| 6 | 175 | 0.10 | 105 | 8.00 | 25.27 | 26.13 | −0.86 |
| 7 | 75 | 0.50 | 105 | 8.00 | 20.15 | 21.52 | −1.36 |
| 8 | 175 | 0.50 | 105 | 8.00 | 24.87 | 24.94 | −0.06 |
| 9 | 75 | 0.10 | 45 | 40.00 | 24.82 | 24.39 | 0.42 |
| 10 | 175 | 0.10 | 45 | 40.00 | 20.99 | 19.88 | 1.11 |
| 11 | 170 | 0.1 | 100 | 12.00 | 27.75 | 27.38 | 0.37 |
| 12 | 175 | 0.50 | 45 | 40.00 | 12.53 | 13.16 | −0.63 |
| 13 | 75 | 0.10 | 105 | 40.00 | 17.90 | 18.99 | −1.09 |
| 14 | 175 | 0.10 | 105 | 40.00 | 21.04 | 21.13 | −0.09 |
| 15 | 75 | 0.50 | 105 | 40.00 | 22.75 | 22.55 | 0.21 |
| 16 | 175 | 0.50 | 105 | 40.00 | 14.46 | 14.98 | −0.51 |
| 17 | 54 | 0.30 | 75 | 24.00 | 24.28 | 24.57 | −0.30 |
| 18 | 195 | 0.30 | 75 | 24.00 | 23.89 | 23.80 | 0.08 |
| 19 | 125 | 0.02 | 75 | 24.00 | 24.49 | 25.08 | −0.59 |
| 20 | 125 | 0.58 | 75 | 24.00 | 26.73 | 26.35 | 0.38 |
| 21 | 125 | 0.30 | 32 | 24.00 | 18.53 | 20.74 | −2.22 |
| 22 | 125 | 0.30 | 117 | 24.00 | 23.04 | 21.03 | 2.01 |
| 23 | 125 | 0.30 | 75 | 1.37 | 16.74 | 16.98 | −0.24 |
| 24 | 125 | 0.30 | 75 | 46.63 | 17.02 | 16.99 | 0.03 |
| 25 | 125 | 0.30 | 75 | 24.00 | 23.53 | 23.58 | −0.05 |
| 26 | 125 | 0.30 | 75 | 24.00 | 24.53 | 23.58 | 0.94 |
| 27 | 125 | 0.30 | 75 | 24.00 | 22.89 | 23.58 | −0.69 |
| 28 | 125 | 0.30 | 75 | 24.00 | 22.53 | 23.58 | −1.06 |
| 29 | 125 | 0.30 | 75 | 24.00 | 23.93 | 23.58 | 0.34 |
| 30 | 125 | 0.30 | 75 | 24.00 | 24.53 | 23.58 | 0.94 |
| Response | 2nd Order Polynomial Equation | Regression (p-Value) | R2 | R2 (Adjusted) | Lack of Fit |
|---|---|---|---|---|---|
| PLQY | 23.63 − 0.1732 X1 + 0.03498 X2 + 0.1905 X3 −0.0802 X4 − 2.38 X1 X2 + 1.61 X1 X3 − 2.68 X1 X4 + 0.1894 X2 X3 − 1.30 X2 X4 – 0.9353 X3 X4 + 0.2905 X21 + 1.07 X22 − 1.38 X23 − 3.36 X24. | 0.0001 | 0.9563 | 0.9155 | 0.1685 |
| Response | 2nd Order Polynomial Equation | Regression (p-Value) | R2 | R2 (Adjusted) | Lack of Fit |
|---|---|---|---|---|---|
| PLQY | −3.3822 + 0.03866 X1 + 22.7576 X2 + 0.1385 X3 + 1.3133 X4 − 0.2379 X1 X2 + 0.0010 X1 X3 − 0.0033 X1 X4 + 0.0315 X2 X3 − 0.4069 X2 X4 − 0.0019 X3 X4 + 0.0001 X21 + 26.8733 X22 − 0.0015 X23 − 0.0131 X24. | 0.0001 | 0.9563 | 0.9155 | 0.1685 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 446.88 | 14 | 31.92 | 23.45 | <0.0001 | significant |
| A-Temperature | 0.5324 | 1 | 0.5324 | 0.3912 | 0.5411 | |
| B-Dosage | 2.14 | 1 | 2.14 | 1.57 | 0.2289 | |
| C-Time | 0.6458 | 1 | 0.6458 | 0.4745 | 0.5014 | |
| D-W/Ace/NaOH | 0.1132 | 1 | 0.1132 | 0.0832 | 0.7770 | |
| AB | 83.27 | 1 | 83.27 | 61.18 | <0.0001 | |
| AC | 38.33 | 1 | 38.33 | 28.16 | <0.0001 | |
| AD | 101.98 | 1 | 101.98 | 74.93 | <0.0001 | |
| BC | 0.5274 | 1 | 0.5274 | 0.3875 | 0.5430 | |
| BD | 24.01 | 1 | 24.01 | 17.64 | 0.0008 | |
| CD | 12.38 | 1 | 12.38 | 9.10 | 0.0087 | |
| A2 | 0.7806 | 1 | 0.7806 | 0.5735 | 0.4606 | |
| B2 | 10.48 | 1 | 10.48 | 7.70 | 0.0142 | |
| C2 | 17.76 | 1 | 17.76 | 13.05 | 0.0026 | |
| D2 | 106.01 | 1 | 106.01 | 77.89 | <0.0001 | |
| Residual | 20.42 | 15 | 1.36 | |||
| Lack of Fit | 16.94 | 10 | 1.69 | 2.44 | 0.1685 | Not significant |
| Pure Error | 3.47 | 5 | 0.6947 | |||
| Cor Total | 467.30 | 29 |
| Std. Dev. | 1.17 | R² | 0.9563 |
|---|---|---|---|
| Mean | 21.40 | Adjusted R² | 0.9155 |
| C.V. % | 5.45 | Predicted R² | 0.7689 |
| Adequate Precision | 17.5186 |
| Std Order | Factor-A Temperature (°C) | Factor-B Dossage (gram) | Factor-C Time (min) | Factor-D Solvent (mL) (H2O/C3H6O/NaOH) | Exp. Actual Value (PLQY%) | RSM Pred. Value | ANN. Pred. Value |
|---|---|---|---|---|---|---|---|
| 1 | 75 | 0.10 | 45 | 8.00 | 14.67 | 14.41 | 12.46 |
| 2 | 175 | 0.10 | 45 | 8.00 | 21.05 | 20.89 | 21.31 |
| 3 | 75 | 0.50 | 45 | 8.00 | 22.80 | 22.35 | 22.74 |
| 4 | 175 | 0.50 | 45 | 8.00 | 19.96 | 19.13 | 19.93 |
| 5 | 75 | 0.10 | 105 | 8.00 | 14.00 | 13.01 | 14.76 |
| 6 | 175 | 0.10 | 105 | 8.00 | 25.27 | 26.13 | 24.84 |
| 7 | 75 | 0.50 | 105 | 8.00 | 20.15 | 21.52 | 19.99 |
| 8 | 175 | 0.50 | 105 | 8.00 | 24.87 | 24.94 | 24.96 |
| 9 | 75 | 0.10 | 45 | 40.00 | 24.82 | 24.39 | 24.51 |
| 10 | 175 | 0.10 | 45 | 40.00 | 20.99 | 19.88 | 21.10 |
| 11 | 170 | 0.1 | 100 | 12.00 | 27.75 | 27.38 | 26.25 |
| 12 | 175 | 0.50 | 45 | 40.00 | 12.53 | 13.16 | 15.80 |
| 13 | 75 | 0.10 | 105 | 40.00 | 17.90 | 18.99 | 17.56 |
| 14 | 175 | 0.10 | 105 | 40.00 | 21.04 | 21.13 | 21.07 |
| 15 | 75 | 0.50 | 105 | 40.00 | 22.75 | 22.55 | 23.82 |
| 16 | 175 | 0.50 | 105 | 40.00 | 14.46 | 14.98 | 18.69 |
| 17 | 54 | 0.30 | 75 | 24.00 | 24.28 | 24.57 | 23.45 |
| 18 | 195 | 0.30 | 75 | 24.00 | 23.89 | 23.80 | 24.89 |
| 19 | 125 | 0.02 | 75 | 24.00 | 24.49 | 25.08 | 24.09 |
| 20 | 125 | 0.58 | 75 | 24.00 | 26.73 | 26.35 | 25.17 |
| 21 | 125 | 0.30 | 32 | 24.00 | 18.53 | 20.74 | 16.69 |
| 22 | 125 | 0.30 | 117 | 24.00 | 23.04 | 21.03 | 23.65 |
| 23 | 125 | 0.30 | 75 | 1.37 | 16.74 | 16.98 | 15.06 |
| 24 | 125 | 0.30 | 75 | 46.63 | 17.02 | 16.99 | 17.38 |
| 25 | 125 | 0.30 | 75 | 24.00 | 23.53 | 23.58 | 23.72 |
| 26 | 125 | 0.30 | 75 | 24.00 | 24.53 | 23.58 | 23.72 |
| 27 | 125 | 0.30 | 75 | 24.00 | 22.89 | 23.58 | 23.72 |
| 28 | 125 | 0.30 | 75 | 24.00 | 22.53 | 23.58 | 23.72 |
| 29 | 125 | 0.30 | 75 | 24.00 | 23.93 | 23.58 | 23.72 |
| 30 | 125 | 0.30 | 75 | 24.00 | 24.53 | 23.58 | 23.72 |
| Hidden Neurons | Train | Validation | Test | All | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | |
| 4-8 * | 0.99 | 0.09 | 0.06 | 0.99 | 0.07 | 0.04 | 0.99 | 0.08 | 0.06 | 0.99 |
| 8-4 | 0.99 | 0.03 | 0.01 | 0.95 | 0.10 | 0.09 | 0.95 | 0.11 | 0.09 | 0.94 |
| 8-16 | 0.99 | 0.04 | 0.03 | 0.78 | 0.17 | 0.13 | 0.96 | 0.12 | 0.09 | 0.93 |
| 9-19 | 0.99 | 0.02 | 0.01 | 0.93 | 0.13 | 0.08 | 0.99 | 0.11 | 0.09 | 0.96 |
| 11-4 | 0.99 | 0.04 | 0.03 | 0.85 | 0.11 | 0.09 | 0.95 | 0.14 | 0.11 | 0.96 |
| 11-7 | 0.99 | 0.02 | 0.01 | 0.97 | 0.07 | 0.06 | 0.82 | 0.12 | 0.09 | 0.97 |
| 11-9 | 0.99 | 0.02 | 0.01 | 0.99 | 0.11 | 0.09 | 0.83 | 0.15 | 0.12 | 0.96 |
| 13-9 | 0.95 | 0.07 | 0.05 | 0.92 | 0.14 | 0.13 | 0.94 | 0.12 | 0.09 | 0.93 |
| 13-13 | 0.99 | 0.03 | 0.02 | 0.76 | 0.11 | 0.09 | 0.93 | 0.16 | 0.13 | 0.95 |
| 17-10 | 0.99 | 0.02 | 0.01 | 0.90 | 0.12 | 0.13 | 0.99 | 0.06 | 0.05 | 0.96 |
| 17-18 | 0.99 | 0.02 | 0.01 | 0.91 | 0.11 | 0.08 | 0.94 | 0.12 | 0.09 | 0.97 |
| 19-4 | 0.99 | 0.03 | 0.02 | 0.52 | 0.12 | 0.09 | 0.97 | 0.12 | 0.09 | 0.96 |
| 19-6 | 0.98 | 0.07 | 0.05 | 0.83 | 0.12 | 0.11 | 0.99 | 0.02 | 0.02 | 0.96 |
| Parameter | Mean | Minimum | Maximum |
|---|---|---|---|
| Total Count | 62 | 62 | 62 |
| Height | 4.054 (nm) | 2.174 (nm) | 8.486 (nm) |
| Area | 2086.516 (nm2) | 381.470 (nm2) | 18,005.371 (nm2) |
| Diameter | 44.032 (nm) | 22.039 (nm) | 151.411 (nm) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yahaya Pudza, M.; Zainal Abidin, Z.; Abdul Rashid, S.; Md Yasin, F.; Noor, A.S.M.; Issa, M.A. Sustainable Synthesis Processes for Carbon Dots through Response Surface Methodology and Artificial Neural Network. Processes 2019, 7, 704. https://doi.org/10.3390/pr7100704
Yahaya Pudza M, Zainal Abidin Z, Abdul Rashid S, Md Yasin F, Noor ASM, Issa MA. Sustainable Synthesis Processes for Carbon Dots through Response Surface Methodology and Artificial Neural Network. Processes. 2019; 7(10):704. https://doi.org/10.3390/pr7100704
Chicago/Turabian StyleYahaya Pudza, Musa, Zurina Zainal Abidin, Suraya Abdul Rashid, Faizah Md Yasin, Ahmad Shukri Muhammad Noor, and Mohammed A. Issa. 2019. "Sustainable Synthesis Processes for Carbon Dots through Response Surface Methodology and Artificial Neural Network" Processes 7, no. 10: 704. https://doi.org/10.3390/pr7100704
APA StyleYahaya Pudza, M., Zainal Abidin, Z., Abdul Rashid, S., Md Yasin, F., Noor, A. S. M., & Issa, M. A. (2019). Sustainable Synthesis Processes for Carbon Dots through Response Surface Methodology and Artificial Neural Network. Processes, 7(10), 704. https://doi.org/10.3390/pr7100704