Linear Analysis of a Continuous Crystallization Process for Enantiomer Separation

Abstract

Continuous preferential crystallization is an innovative approach to the separation of chiral substances. The process considered in this work takes place in a gently agitated fluidized bed located in a tubular crystallizer. The feasibility of the process has been shown in previous work, but it also turned out that choosing suitable operation conditions is quite delicate. Hence, a model based process design is desirable. Existing models of the process are rather complicated and require long computational times. In this work, a simple linear dynamic model is suggested, which captures the main properties of the process. The model is distributed in space and in a property coordinate. Using the method of characteristics, a semi-analytical solution of the linear model is derived. As a challenge to the solution, there is a recycle loop in the process that causes a feedback and couples the boundary conditions at different boundaries of the computational domain. In order to deal with this, a numerical scheme is suggested. The semi-analytical solution provides a deeper insight into the process dynamics. A comparison with a more detailed mathematical model of the process and with experiments shows strengths and limitations of the linear model.

1. Introduction

Chiral substances consist of two types of molecules, which are non-superimposable mirror images of each other and are called enantiomers; usually the two types are denominated as D and L [1]. Chiral substances frequently occur in the life science industries. Typically, they are synthesized as a racemic 50:50% mixture of both enantiomers. The D and the L enantiomer often have completely different effects on biological organisms or the human body, one of them occasionally being harmful or even toxic. Therefore, there is a need to produce enantiomers in pure form by separating the racemic mixture. As both enantiomers have identical physical and chemical properties in non-chiral environments, their purification is a challenging task that requires advanced separation techniques [2]. One possible approach is to use crystallization-based methods.

1.1. Continuous Enantioseparation by Preferential Crystallization

Preferential crystallization is a method for direct crystallization of a single enantiomer out of a racemic solution. It is applicable, if the chiral system occurs as conglomerate—i.e., if the enantiomers crystallize as separate enantiopure crystals [3,4]. Continuous processes for preferential crystallization have been suggested in [5,6,7]. A simple process variant is shown in Figure 1. The system consists of a feed tank containing a racemic liquid mixture, and of a tube shaped crystallizer. The liquid from the tank is fed as over-saturated solution flowing from the bottom of the crystallizer to the top of the crystallizer. Initially, the crystallizer is seeded with crystals of the desired enantiomer—e.g., the L enantiomer. Under suitable operation conditions, only the L crystals grow, whereas the D enantiomer is kept in the liquid phase. Big crystals sinking to the bottom of the crystallizer are recycled in a mill, which breaks the crystals into smaller fragments and sends them back to the crystallizer. Product crystals are removed from the crystallizer via an outlet at the side of the crystallizer, which is operated in a pulse-wise manner. The vertical position of the outlet determines the size of the product crystals. The liquid phase leaving the crystallizer top is sent back to the feed tank. The process can be extended by a second crystallizer in order to recover both enantiomers in pure form.

The feasibility of the process has been proven in experiments [5,7,8]. It was found that the operation window for successful separation is quite small. Further, the nucleation of the counter-enantiomer can never be fully prevented. The process counteracts the product contamination by a self-cleaning effect: the fluid flow flushes small crystals and nuclei out of the crystallizer top. This effect depends on the liquid flow rate. A high flow rate supports the removal of nuclei and increases purity, but on the other hand, also washes out desired L crystals and reduces productivity.

1.2. Previous Simulation Models and Objectives of This Work

In previous publications, models of the described process have been presented and compared to experimental results [7,9]. The main focus used to be on productivity and the size distribution of the product crystals. The purity of the product has so far been less considered, one reason being that it is quite hard to obtain reliable kinetic expressions for nucleation, because the nucleation mechanisms in the process are not fully understood [8]. The objective of this work is to derive criteria for product purity that are easier to evaluate. For this purpose, a very simple linear model is developed in the next section. The method of characteristics is used to solve the model equations and derive guidelines for product purity. In Section 3, comparisons are made with the more detailed models and experimental results.

2. Minimal Linear Process Model

In this section, a rather simple model of the separation process is constructed. The aim is to obtain a representation of the process that allows for an analytical solution and gives insight into essential qualitative properties of the process.

2.1. Model Assumptions

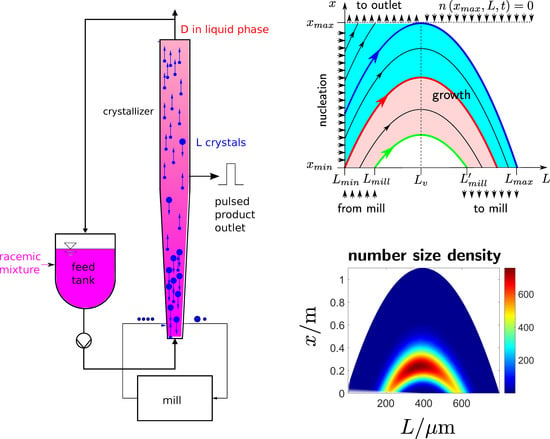
The geometry of the crystallizer is described by a single space coordinate x in the direction of the fluid flow. The fluid inlet point at the bottom of the crystallizer and the fluid outlet point at the top are denoted as $x_{min}$ and $x_{max}$, respectively. Gradients perpendicular to the x coordinate are neglected.

The properties of the crystal population depend on a single property coordinate L representing a characteristic crystal length. The number size density n of the crystals (number of crystals per crystal size and volume) is a function of L, x, and of time t. The computational domain of n is shown in Figure 2.

Gravity and drag forces cause the movement of the crystals in space. For simplicity, the interaction between crystals is neglected. Hence, the crystal velocity v is only a function of L and x. For small crystals, the drag force dominates and pushes the particles upwards ($v(L,x)>0$), whereas gravity causes the larger crystals to sink to the bottom ($v(L,x)<0$). For a certain crystal size $L_v\left(x\right)$, gravity and drag force cancel each other, and the crystal is in mechanical equilibrium and not moving, $v(L_v\left(x\right),x)=0$.

As a strong simplification, it is assumed that the composition of the liquid phase does not change, and that the supersaturation in the liquid phase is approximately constant. This is only valid for high liquid flow rates. More detailed models for the liquid phase have been published in [7,9,10,11,12]. As a consequence of this assumption, the crystal growth rate $G>0$ and the nucleation rate B are constant over space. Nuclei have a characteristic length $L_{min}$. The same growth rate and nucleation rate are assumed for the desired L enantiomer and the undesired D enantiomer.

A population balance results in the following equation for the number size density $n(L,x,t)$:

$$\frac{{\displaystyle \partial n}}{{\displaystyle \partial t}}+v(L,x)\frac{{\displaystyle \partial n}}{{\displaystyle \partial x}}+G\frac{{\displaystyle \partial n}}{{\displaystyle \partial L}}=0$$

(1)

Crystals sinking to the bottom of the crystallizer are ground in a mill and returned as seeds to the crystallizer. It is assumed that the share of crystals coming out of the mill with a certain size L is always the same and is equal to ${\overline{n}}_{mill}\left(L\right)$. The maximum size of the crystals out of the mill is limited to $L_{mill}$, which, for example, may be the gap between the mill’s rotating blade and its stationary parts.

The number size density at the mill outlet reads

$$n_{mill}(L,t)={\widehat{n}}_{mill}\left(t\right)·{\overline{n}}_{mill}\left(L\right)$$

(2)

with a time dependent scaling factor ${\widehat{n}}_{mill}\left(t\right)$ following from a mass balance of the mill. Assuming that the mill has negligible hold-up, the total mass of crystals leaving the mill must always be identical to the total mass of crystals entering the mill:

$$\underset{L_{min}}{\overset{L_{mill}}{\int }}{n}_{mill}(L,t)L^{3}dL=\underset{L_v\left(x_{min}\right)}{\overset{\infty }{\int }}n(L,x_{min},t)L^{3}dL.$$

(3)

The combination of (2) and (3) leads to the boundary condition

$$n(L,x_{min},t)={\overline{n}}_{mill}\left(L\right)\frac{{\displaystyle \underset{L_v}{\overset{\infty }{\int }}n(L,x_{min},t)L^{3}dL}}{{\displaystyle \underset{L_{min}}{\overset{L_{mill}}{\int }}{\overline{n}}_{mill}\left(L\right)L^{3}dL}}for{L}_{min}\le L\le L_{mill}.$$

(4)

The corresponding boundary condition at the crystallizer top reads

$$n(L,x_{max},t)=0\mathrm{f}\mathrm{o}\mathrm{r}L\ge L_v\left(x_{max}\right),$$

(5)

because no particles are fed to the crystallizer top.

The boundary along the x-coordinate depends on the nucleation of crystals. It reads

$$Gn(L_{min},x,t)=B\mathrm{f}\mathrm{o}\mathrm{r}{x}_{min}<x<x_{max}.$$

(6)

An initial condition

$$n(L,x,0)=n_0(x,L)$$

(7)

completes the model.

2.2. Analytical Solution of the Linear Model by the Method of Characteristics

The method of characteristics is an established method for the analysis of separation processes with negligible dispersion [13]. In this work, it provides an approach for the solution of the model system (1) and (4)–(7). The size distribution is calculated along an arc with arc length parameter s, i.e., $n\left(s\right)=n\left(L\right(s),x(s),t(s\left)\right)$. The total derivative with respect to s reads

$$\frac{{\displaystyle dn}}{{\displaystyle ds}}=\frac{{\displaystyle \partial n}}{{\displaystyle \partial L}}\frac{{\displaystyle dL}}{{\displaystyle ds}}+\frac{{\displaystyle \partial n}}{{\displaystyle \partial x}}\frac{{\displaystyle dx}}{{\displaystyle ds}}+\frac{{\displaystyle \partial n}}{{\displaystyle \partial t}}\frac{{\displaystyle dt}}{{\displaystyle ds}}.$$

(8)

A comparison of (8) with the population balance (1) leads to the following set of equations:

$$\begin{array}{ccc}\hfill \frac{{\displaystyle dt}}{{\displaystyle ds}}& =& 1\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \frac{{\displaystyle dx}}{{\displaystyle ds}}& =& v(L,x)\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \frac{{\displaystyle dL}}{{\displaystyle ds}}& =& G\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill \frac{{\displaystyle dn}}{{\displaystyle ds}}& =& 0\hfill \end{array}$$

(12)

From (9), it is obvious that the arc length parameter s is identical to the progress in time. Equation (12) shows that the number size density does not change when moving along a characteristic curve—i.e.,

$$n(L,x,t)=n(L_1,x_1,t_1),$$

(13)

where $L_1,x_1,t_1$ is an arbitrary reference point on the same characteristic. Note that (13) does not mean that at one moment in time, the number size density n has the same value along the characteristic – t and $t_1$ are different time points. Instead, (13) says that the number of crystals in a small fluid element moving along a characteristic does not change, whereas the size of the crystals in the fluid element does.

In the remainder of this subsection and in the next subsection, a very simple velocity profile is studied. It is assumed that the crystal velocity decreases linearly with the crystal size and does not depend on the space coordinate:

$$v\left(L\right)=v_0-v^{\prime }·(L-L_{min}),$$

(14)

where $v_0$ is the velocity of the nuclei identical to the fluid flow velocity, and $-v^{\prime }$ is a constant slope. The extension to a more general velocity profile is outlined in Section 2.5.

In the case of this simple velocity profile, the solution of (9)–(12) is straightforward. From (11), one gets

$$L=L_1+G·(s-s_1)=L_1+G·(t-t_1).$$

(15)

From (10), in combination with (15) and (14), one obtains

$$x=x_1+v\left(L_1\right)·(s-s_1)-\frac{{\displaystyle v^{\prime }}}{{\displaystyle 2}}G·{(s-s_1)}^2=x_1+v\left(L_1\right)·(t-t_1)-\frac{{\displaystyle v^{\prime }}}{{\displaystyle 2}}G·{(t-t_1)}^2$$

(16)

With the help of (15), the arc length parameter s or the time t is eliminated from (16). This gives an explicit equation for the characteristic curve in the L-x-plane:

$$x=x_1+v\left(L_1\right)·\frac{{\displaystyle L-L_1}}{{\displaystyle G}}-\frac{{\displaystyle v^{\prime }}}{{\displaystyle 2}}·\frac{{\displaystyle {(L-L_1)}^2}}{{\displaystyle G}}.$$

(17)

It follows that the characteristic lines are parabolas in the L-x-plane (see Figure 3a). For all of them, the vertex is at

$$L_v=L_{min}+\frac{{\displaystyle v_0}}{{\displaystyle v^{\prime }}},$$

(18)

where the particle velocity vanishes and the crystals are at mechanical equilibrium.

Figure 3b shows that four different regions may be distinguished in the L-x-plane. Region 1 (shaded blue in the figure) contains all characteristic curves that start on the x-axis. The number of crystals in this region depends on the nucleation rate. To obtain the number size density at any point in the region, one has to go back in time until the characteristic curve intersects the x-axis. The number size density is equal to the number of crystals nucleated at that time. From (6): $n=B/G$. Region 1 is further divided into a subregion (a) containing crystals that escape through the top of the crystallizer, and into a subregion (b) with crystals that sink to the bottom of the crystallizer and are recycled in the mill. The distinction between subregions (a) and (b) is important for the process operation. On the one hand, as many crystals of the desired enantiomer as possible should be kept in the system. On the other hand, undesired nuclei of the counter-enantiomer should be flushed out of the crystallizer before they grow large and contaminate the product. Subregion 1 (a) and 1 (b) are separated by the characteristic curve highlighted blue in Figure 3b. This is the characteristic of nuclei moving up to the highest point $x_{max}$ of the crystallizer and sinking to the bottom afterwards. The end point of that characteristic on the L-axis marks the biggest size $L_{max}$ that the crystal can reach for the chosen operation conditions. From an elementary calculation, one obtains

$$L_{max}=L_{min}+\frac{{\displaystyle v_0}}{{\displaystyle v^{\prime }}}+\sqrt{2\frac{{\displaystyle G}}{{\displaystyle v^{\prime }}}(x_{max}-x_{min})}.$$

(19)

Region 2 (shaded red in the figure) is formed by all characteristics starting on the L-axis. All crystals in Region 2 were generated in the mill. In order to determine the number size density at some point $(x,L)$ in that region, one has to go back in time to the point where the characteristic curve intersects the L axis and where $x=x_{min}$. The number size density $n(x,L)$ is equal to the number of crystals generated in the mill at that time. The upper border of Region 2 is the characteristic curve highlighted red in Figure 3b, which starts at $(L_{min},x_{min})$. If the vertex of this characteristic curve has an x-coordinate smaller than $x_{max}$, then all crystals in Region 2 remain in the process permanently, rising from the mill, sinking to the bottom of the crystallizer and returning to the mill. The lower border of Region 2 (highlighted green in the figure) is given by the characteristic curve of the largest crystals coming out of the mill with size $L_{mill}$.

Region 3 is the area below the green characteristic. No crystals exist in that region, except when they are introduced from outside, but even in this case, they will vanish quickly.

Region 4 in the upper right corner of the diagram is another crystal free area. The reason is that no large crystals are fed into the crystallizer from the top.

The residence time T of the crystals in the crystallizer is easily calculated from the characteristics. It is identical to the arc length of the crystals’ characteristic curve $T=t_{end}-t_1=s_{end}-s_1$, where $L_1,x_1,s_1$ denote the starting point of the characteristic either on the x axis (with $L_1=L_{min}$ ) or on the L axis (with $x_1=x_{min}$), and $L_{end},x_{min},s_{end}$ is the end point on the L axis. From (16), one gets

$$x_{min}=x_1+v\left(L_1\right)T-\frac{{\displaystyle v^{\prime }}}{{\displaystyle 2}}G{T}^2,$$

(20)

or, after solving for T:

$$T=\frac{{\displaystyle v\left(L_1\right)}}{{\displaystyle v^{\prime }G}}+\sqrt{{\left(\frac{{\displaystyle v\left(L_1\right)}}{{\displaystyle v^{\prime }G}}\right)}^2+2\frac{{\displaystyle x_1-x_{min}}}{{\displaystyle v^{\prime }G}}}.$$

(21)

The crystals with the shortest residence time $T_{min}$ are those on the characteristic curve marked as a thick green line in Figure 3. These are the largest crystals coming out of the mill with $L_1=L_{mill},x_1=x_{min}$. From (21), it follows that their residence time is

$$T_{min}=2\frac{{\displaystyle v\left(L_{mill}\right)}}{{\displaystyle v^{\prime }G}}.$$

(22)

The biggest residence time $T_{max}$ belongs to the crystals on the characteristic curve marked as a thick blue line in Figure 3. These are the crystals that rise to the highest point in the crystallizer and subsequently, after sinking to the bottom, reach the largest particle size. After some calculations, one gets

$$T_{max}=\frac{{\displaystyle v_0}}{{\displaystyle v^{\prime }G}}+\sqrt{2\frac{{\displaystyle x_{max}-x_{min}}}{{\displaystyle v^{\prime }G}}}.$$

(23)

In conclusion, the solution of the process model (1) and (4)–(7) is quite simple, when moving along the characteristic lines. The situation is complicated by the mill, which forms a feedback loop between large crystals sinking to the bottom and small crystals entering the crystallizer. The treatment of that feedback loop is discussed in the next section.

2.3. Solution of the Linear Model by Stepping Forward in Time with a Problem Specific Step Size

Figure 4 illustrates how the feedback loop caused by the mill can be tackled. At time $t=0$, the number size density $n(L,x,0)$ is completely known because of the initial condition (7). The diagram in Figure 4a shows straight lines representing crystals that will arrive in the mill at the same time. In a first time interval equal to the minimum residence time $T_{min}$ of the crystals, the input to the mill only depends on the initial conditions. For a time $0<t<T_{min}$, the input to the mill is

$$n(L,x_{min},t)=n(L_1,x_1,0)for{L}_{mill}^{\prime }<L<L_{max}.$$

(24)

In the above equation, $(L_1,x_1)$ stands for the point on the characteristic through $(L,x_{min})$ that is reached when going back an arc length t on that characteristic. $L_{mill}^{\prime }$ is the size of the largest crystals coming out of the mill, after they have sunk to the crystallizer bottom (see Figure 3b). All crystals going into the mill between $t=0$ and $t=T_{min}$ are indicated by black lines in Figure 4a.

The outcome of the mill for the time interval $0<t<T_{min}$ is calculated by inserting (24) into the integral on the right-hand side of Equation (4). The crystals coming out of the mill before time $T_{min}$ are represented by the black lines in the right-hand side diagram of Figure 4.

During the same time interval, the crystals in the red region (coming out of the mill) and the blue region (generated by nucleation) in Figure 4a move to the regions with the same color in Figure 4b, without changing their number. The number size densities in the red and blue regions in the right-hand side diagram at time $T_{min}$ are just copies of the number size densities at time $t=0$ in the left-hand side diagram.

The number size densities in the white unshaded area of the right-hand side diagram depend on nucleation and can be determined with Equation (6).

In summary, the number size density $n(L,x,T_{min})$ can be calculated completely from the number size density $n(L,x,0)$ by analytical calculations, provided that the integrals in Equation (4) have elementary antiderivatives. However, the analytical solution is not particularly useful, as it tends to become very complicated after a few steps, even for a computer algebra system. Therefore, a numerical time stepping scheme is presented in the following section. An analytical solution of a very simple case will be used at the end of this section to test the accuracy of the numerical solution.

For the numerical solution, an initial grid is chosen as shown in the diagram on the left-hand side of Figure 5. The grid points lie on straight lines, which indicate a certain distance in time required to reach the bottom of the crystallizer and the entrance to the mill. The time interval between two neighboring straight lines is always equal to the same value $\Delta t=T_{min}/M$, M, being a free parameter. N equidistant grid points are chosen on the L axis between $L_{mill}^{\prime }$ and $L_{max}$. The intersection between the characteristics through those points with the straight lines defines the remaining grid points at $t=0$. As previously explained, one can calculate where the crystals on the grid points at $t=0$ will be at time $t=T_{min}$, just by tracing back the characteristics. Crystals at the blue and red grid points in Figure 5 move inside the crystallizer in the considered time interval, but do not reach the mill. Their number size densities at time $T_{min}$ are just copies of the number size densities at time $t=0$ of the corresponding points in Figure 5a. More effort is required for the crystals that pass the mill before time $T_{min}$. These points are marked black in Figure 5a,b. The number size densities at the black points at time $T_{min}$ (Figure 5b) are computed from the number size densities at time $t=0$ (Figure 5a) with the help of Equation (4); the trapezoidal rule is used to approximate the integrals. As a challenge for the numerical approach, the black points in Figure 5b are no longer a part of the original grid. Instead, they are used to calculate the number size densities at the white points Figure 5b, which are still undefined. This is done by linear interpolation in the following way:

• The black points in Figure 5b, leaving the mill at the same time, are connected by green lines. The intersection points between the green and the black grid lines are determined (green points in the figure).
• The number size densities at the intersection points are computed by linear interpolation along the green lines.
• The number size densities at the white points are computed by linear interpolation along the black lines.

Finally, the number size densities at some further grid points, shown as light-blue points, are given by the boundary condition (6). This concludes a step forward in time with step length $T_{min}$. As the algorithm is only a linear mapping from the number size densities on the grid at $t=0$ to the number size densities on the same grid at $t=T_{min}$, it can be solved very efficiently in Matlab.

The numerical algorithm has two sources of inaccuracies: the integration by the trapezoidal rule and the linear interpolation. In order to validate the algorithm, it is compared with the analytical solution for a very simple testing case that has no physical relevance, but is only chosen because it allows an analytical solution of the integrals in (4). The initial number size density of the testing case is chosen as

$$N(L,x,0)=a·(L-L_{min})+b·(x-x_{min}),$$

(25)

with $a=10/(L_{max}-L_{min})$ and $b=5/(x_{max}-x_{min})$. The number size density of the crystals leaving the mill is obtained from

$${\overline{n}}_{mill}\left(L\right)=sin\left(\frac{{\displaystyle L-L_{min}}}{{\displaystyle L_{mill}-L_{min}}}\right).$$

(26)

The numerical and the analytical solutions at $t=T_{min}$ are compared for different values of the grid parameters M and N. The error is defined as the Frobenius norm of the difference between the numerically and the analytically computed number size density at all grid points, divided by the Frobenius norm of the analytical number size density. As can be seen from Figure 6, the error is already quite small for a very coarse grid. A good compromise between systematic and rounding errors is achieved for $N\approx 40$ grid points per grid line. The number M of grid lines is of a minor importance for this specific example.

2.4. Numerical Results

Numerical computations are done using the parameter values from

Table 1. Parameter values used in the simulations. The same nucleation rate B and growth rate G are assumed for both the desired enantiomer and the counter-enantiomer.

Symbol	Value	Meaning
B	$1\times {10}^{-5}{m}^{-3}{s}^{-1}$	nucleation rate
G	$1\times {10}^{-8}m{s}^{-1}$	growth rate
$L_{mill}$	$390\times {10}^{-6}m$	largest crystals out of the mill
$L_{min}$	$1\times {10}^{-6}m$	size of nuclei
$v_0$	$5.3\times {10}^{-5}m{s}^{-1}$	liquid flow velocity
$v^{\prime }$	$0.135s^{-1}$	velocity gradient
$x_{min}$	$0m$	crystallizer bottom position
$x_{max}$	$1.1m$	crystallizer top position

. The parameter values are chosen as close as possible to the simulation conditions of the more detailed model in [7], although there are some systematic differences between the models. This will be discussed in Section 3.

It is assumed that the crystals coming out of the mill have a bell curve-shaped distribution,

$${\overline{n}}_{mill}\left(L\right)=\left\{\begin{array}{cc}exp\left(-\frac{{\displaystyle {(L-\mu )}^2}}{{\displaystyle 2{\sigma }^2}}\right)\hfill & \mathrm{f}\mathrm{o}\mathrm{r}{L}_{min}\le L\le L_{mill},\hfill \\ 0\hfill & \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}.\hfill \end{array}\right.$$

(27)

Initially, a small amount of seed crystals of the desired L enantiomer are placed in the middle of the crystallizer. Figure 7 shows snapshots of the crystal populations at different time points that are multiples of the minimum residence time, which under the chosen conditions is equal to $T_{min}=718s$. The crystal populations are represented by mass related size distributions $q_3$, defined as

$$q_3(L,x,t)=n(L,x,t)·L^3$$

(28)

At the beginning, the crystallizer is completely free from undesired D crystals. The liquid flow velocity $v_0$ is chosen such that no crystals, apart from the nuclei in region 1a of Figure 3, can leave the process, and the crystal mass grows exponentially. Additionally, nuclei of the D crystals in region 1b remain in the crystallizer. Therefore, crystals of the counter-enantiomer D gradually accumulate in the crystallizer.

After 20 time steps, the bulk of the L crystals reach the mill and the first recycled fragments of the L crystal are moved upwards. One may also recognize a small population of D crystals rising in the crystallizer (encircled in the diagram).

After 120 time steps, the first D crystals have also passed the mill. The L crystals slowly approach the final bimodal distribution.

For longer times, the L and D crystal distributions become more and more similar to each other, although the absolute numbers of L and D crystals are very different. Especially in the lower half of the crystallizer, one may observe a counter-flow of small crystals moving up and large crystals sinking down. The resulting bimodal distribution differs from the first intuition that crystals should be sorted according to their size with small crystals at the top and large crystals at the bottom. This is only true for the larger half of the crystals.

Figure 8 shows the total mass of crystals in the crystallizer over time. For the chosen conditions, hardly any crystals escape through the crystallizer top. Hence, both the mass of the L crystals and the mass of the D crystals grow exponentially. Note that this does not cause a decrease in the purity of the crystal phase. The L crystals keep their initial lead in mass over the D crystals, and the contamination of the crystal phase remains low. This is visualized in Figure 8b containing the purity of the crystal phase, which is defined as the mass of the L crystals defined by the total crystal mass.

2.5. Possible Extensions of the Linear Model

The linear model contains a number of strongly simplifying assumptions. The topic of this section is to discuss, how some of these assumptions may be relaxed in order to bring the simulation results closer to reality.

So far, it has been assumed that B is constant in time and space. However, in reality, B varies due to the spatially varying supersaturation of the liquid phase. Further, experimental results in [8] indicate that the nucleation mainly takes place at the crystallizer walls and, therefore, may be different at different points in the crystallizer and may also change over time, when crystals adhere to the walls. A time and space dependent nucleation rate $B(x,t)$ would hardly have an effect on the proposed solution approach for the linear model. All described solution steps are applicable to a varying nucleation rate, too.

In a similar way, a space and time dependent growth rate G could be taken into account; however, this might require a numerical solution of Equations (9)–(12).

A more detailed description of the crystal velocity is also possible, but requires a higher effort. The linear expression for the particle velocity (14) has the advantage that it allows analytical calculations, but it neglects some aspects of experimental reality. First, the experimental crystallizer has a conical shape with a diameter increasing from the bottom to the middle of the tube. This causes a decreasing liquid flow velocity in the empty tube and also makes the particle velocity dependent on the space coordinate x. Second, the linear dependence of the particle velocity on the characteristic size L is a rather crude approximation. The classic model by Richardson and Zaki [14] gives a more realistic picture of the particle velocity and has been applied successfully to the continuous enantiomer separation in [7,9].

To obtain the particle velocity $v_P(L,x)$ according to the model by Richardson and Zaki, first the Archimedes number (describing the ratio between buoyancy and friction force on a particle of size L) is calculated from

$$Ar\left(L\right)=\frac{{\displaystyle g{\widehat{L}}^3{\rho }_f\left({\rho }_P-{\rho }_f\right)}}{{\displaystyle {\mu }_f^2}},$$

(29)

where $\widehat{L}=L/\mathsf{\Psi }$ is the size of an equivalent spherical particle and $\mathsf{\Psi }$ is a shape dependent sphericity parameter. The fluid velocity $v_{eq}$ needed to keep a single particle of size L in equilibrium follows from

$$v_{eq}\left(L\right)=\frac{{\displaystyle R{e}_{eq}\left(L\right){\mu }_f}}{{\displaystyle \widehat{L}{\rho }_f}},$$

(30)

with the Reynolds number

$$R{e}_{eq}\left(L\right)={\left(-3.809+{\left(3.{809}^2+1.832Ar{\left(L\right)}^{0.5}\right)}^{0.5}\right)}^2.$$

(31)

For higher particle densities, $v_{eq}$ has to be corrected in the following way to account for particle-particle interactions:

$$v_{eq}^{*}\left(L\right)=v_{eq}\left(L\right){ϵ}^{m\left(L\right)}$$

(32)

with the fluid volume fraction $ϵ$ and

$$\frac{4.8-m\left(L\right)}{m\left(L\right)-2.4}=0.043Ar{\left(L\right)}^{0.57}.$$

(33)

Finally, the particle velocity $v_P(x,L)$ is computed from

$$v_P(x,L)=\frac{{\displaystyle \dot{V}}}{{\displaystyle A\left(x\right)}}-v_{eq}^{*}(x,L,t),$$

(34)

where $A\left(x\right)$ is the cross-sectional area of the crystallizer at position x. In this contribution, the model is simplified a bit by assuming a constant fluid volume fraction $ϵ=0.8$. Due to the conical crystallizer shape, the cross-sectional area $A\left(x\right)$ depends on the space coordinate x. Figure 9a shows particle velocity profiles at different positions in the crystallizer for a constant liquid flow rate. The linear velocity profile used so far is a rough average of these profiles.

The computation of the characteristics with the particle velocity by Richardson and Zaki requires a numerical integration of (9)–(12). From Figure 9b, one can see that the result is not too different from the simple approach in Figure 3. For small crystal sizes L, the characteristics are still roughly parabola shaped, but for large crystals, there are clear deviations. Lines connecting crystals that will reach the mill at the same time (blue) or connecting crystals having left the mill at the same time (red) are no longer straight lines, but curves. Apart from that, important qualitative results obtained for the linear velocity profile are still valid for the Richardson-Zaki model. One can still distinguish one area in the L-x-plane, where crystals from the mill are permanently recycled, and an area in which all crystals originate from nucleation. The two areas are separated by the characteristic through $(L_{min},x_{min})$, shown as a thick green line. The highest point of that characteristic determines if nuclei can accumulate in the crystallizer or not. If the highest point lies above the crystallizer top, all nuclei escape through the outlet and high product purity is guaranteed at all times. This can be achieved by adjusting the liquid flow rate, as illustrated in Figure 9c showing the characteristic through $(L_{min},x_{min})$ for different liquid flow rates.

The numerical solution of the more detailed model by the time stepping scheme is also possible in principle. The main difference in this case is that the grid points have to be computed numerically.

3. Comparison with the Detailed Model and Experiments

A more detailed nonlinear model of the process has been presented in [7], which agrees well with experimental results. The model differs from the linear model of this work in several aspects. First, the conical shape of the crystallizer is taken into account. Further, the detailed model includes a liquid phase with varying super-saturation and an energy balance capturing temperature gradients in the crystallizer. Growth and nucleation rates are described by experimentally validated kinetics, which depend on the local supersaturation, and hence change over space and time. The movement of the particles is described by the Richardson-Zaki model. Finally, the detailed model includes the pulse-wise removal of product crystals of the experimental process.

Due to the differences between the model from [7] and the linear model, a direct quantitative agreement can hardly be expected. Nevertheless, it seems worthwhile doing a qualitative comparison between the models in order to validate the linear model and highlight its shortcomings.

The first difference is that the linear model neglects particle-particle interactions. Therefore, the crystal mass grows exponentially towards infinity. In the full model, there is a feedback mechanism that limits the volume fraction of the particles. If the particle volume fraction gets too big and the liquid volume fraction $ϵ$ becomes small, the particle velocity is increased according to Equation (32). In the linear model, this mechanism is missing. Therefore, the validity of the linear model is limited to small particle concentrations.

A second difference concerns the purity of the crystal phase. A simulation result with the detailed model is shown in Figure 10 (parameter values are given in [7]). The figure contains the product purity of the detailed model, which is equal to the purity of the crystal phase in a short segment of the crystallizer around the product outlet. It is compared to the purity of the linear model’s crystal phase, which, after a initial transient phase, is approximately the same at all points in the crystallizer. One can see in Figure 10 that, initially, for the first 50 h of operation, the linear model and the detailed model predict high purity and agree quite well qualitatively. However, for longer times, a drop in the product purity is observed in the detailed model. The reason may be that the detailed model contains dispersive terms accounting for back-mixing, whereas the linear model assumes perfect plug flow. Apparently, the back-mixing causes a slow accumulation of undesired crystals, also because the crystals in region 1a of Figure 3 may remain in the crystallizer. One consequence is that, if the detailed model is correct, the process may require an occasional cleansing after a long operation time. The other consequence is that the validity of the linear model is limited to shorter operation times. In experiments, a slow contamination of the product has not been found [8]. The purity of the product remained high for operation times of up to 10 h. The experimental purity is slightly lower than the simulated values, which may be explained by the uncertainties in the simulated nucleation rates, or by uncertainties in the measurements.

4. Conclusions

The proposed linear model for the continuous preferential crystallization process gives a convenient way to estimate residence times of the crystals and purity of the crystal phase. One outcome of this work is a rigorous mathematical criterion that guarantees permanent purity in the case of negligible back-mixing of the fluid flow. The criterion requires the calculation of a single characteristic curve. It is based on the particle velocity and the growth rate of the crystals, for both of which reasonable estimates exist in most cases. The criterion is independent of the nucleation rate, which is quite hard to determine in experiments. The criterion gives a minimum liquid flow rate, above which the crystallizer should be operated. Above that flow rate, nucleated crystals are completely flushed out of the process before they can reach a size that allows the crystals to sink to the bottom.

In experiments, the liquid flow rate is usually kept a bit below this limit in order to increase productivity. It is found that, also in this case, high purities can be achieved. The simple model gives a qualitative explanation for this. Although nuclei may theoretically accumulate in the crystallizer and contaminate the product, the simultaneous mass increase in the desired crystals compensates this. However, when operating the crystallizer below the theoretical minimum flow rate, the purity is quite strongly affected by the nucleation rate.

The simple linear model studied in this work may also be useful for process optimization or control purposes. Its main advantage is that the numerical solution only requires a linear mapping from one number size density to another number size density with a fixed time step and, therefore, can be done very efficiently.