1. Introduction
It is known in nonlinear chromatography that the separation process and the migration rate of sample components through a porous stationary phase are highly influenced by the adsorption isotherms of each component. For a system that contains more than one component at a sufficient concentration (multicomponent system), their adsorption in the stationary phase will be influenced by each other, so it is important to determine their isotherms in a competitive form, which are called ‘competitive isotherms’, whereas the single-component isotherm is a useful tool to give information about the adsorption in a single-component system. The suitable choice of the isotherm model and obtaining the adsorption data in a wide range of concentrations of the studied components allow the possibility of prediction of the elution band profiles for the optimization of the separation process [
1].
In case of overloading the chromatographic column with a high concentration of a binary mixture, the separation process occurs in the nonlinear range of the adsorption isotherms, and the molecules will interfere with each other for adsorption in the stationary phase [
2]. The same phenomenon in SFC is expected to occur between the modifier and the additive molecules as a consequence of using a ternary mobile phase (CO
2 + modifier + additive) for the separation of polar solutes. Our work is considered an attempt to elucidate the adsorption process of the mixture of modifier and additive on a polar stationary phase in SFC because there is still a lack of information in describing the adsorption behavior of their mixture.
Over the last decade, greater interest has emerged in SFC-related studies dealing with adsorption isotherm determination [
3,
4,
5,
6,
7,
8]—on the one hand, for the purpose of comparison between the used methods for the isotherm determination, and on the other hand, for the adsorption study of the binary mobile phase in different stationary phases. Most of the equilibrium isotherm measurements in liquid chromatography have been made using dynamic methods, which are more accurate and faster than static methods. For those reasons, the same strategy will be followed with SFC [
3].
Enmark et al. [
4] compared the results of adsorption isotherm determinations of antipyrine on a Kromasil silica column using CO
2–methanol as eluent. The data were calculated by the methods of elution by characteristic points (ECP), retention time method (RTM), inverse method (IM), and perturbation peak (PP) method. They concluded that they could not predict the elution profile of the studied compound with the isotherm data obtained via the PP method.
Glenne et al. [
5] used the tracer pulse method and the elution by the characteristic point method to calculate the adsorption isotherms of the most often used co-solvents in SFC (methanol, acetonitrile, 2-propanol, and ethanol) using 100% CO
2 as eluent on different chemistries of the stationary phase Kromasil Diol, Kromasil Silica, and Princeton 2-ethylpyridine (2-EP).
In chiral SFC separations, Kamarei et al. [
6] applied five dynamic methods to calculate the adsorption isotherms of the naproxen enantiomers using mixtures of CO
2 and methanol or ethanol on the chiral column Kromasil Whelk-O1. They found that the inverse method produced the best agreement between the experimental and calculated elution profiles. Kamarei et al. [
7] chose the frontal analysis method to measure the equilibrium data of S-naproxen on the Whelk-O1 column with a modified SFC system (they reduced the large dead volume of tubing, connections, and the mixer volume). The results of the adsorption isotherm estimation improved significantly compared to the original system. Rédei et al. were able to show the displacement effect of methanol as a sample solvent on the elution of alkylbenzenes by determining the adsorption isotherms on the alkylamide C18 ABZ+plus column for methanol and the concerned components of the sample [
8]. Recently, Kazmouz et al. measured the surface excess isotherm of methanol on end-capped reversed stationary phases under subcritical and supercritical conditions using the minor disturbance peak method. They found very small differences in the surface excess adsorption isotherm for methanol between the two conditions, and they found that the methanol excess adsorption in the stationary phase embedded with amide (polar group) is higher than on the C
18 column without functional groups [
9]. The variation of methanol (modifier) adsorption on a Kromasil diol column with temperature and pressure was studied by Glenne et al., showing that the adsorption was higher at low pressure (110 bar) and high temperature 55 °C than at high pressure (310 bar) with the same temperature [
10].
In packed column SFC, the possibility of employing water as a mobile phase additive is limited by its miscibility with carbon dioxide, which is very low (∼0.1%,
w/
w) in supercritical CO
2 [
11], although the solubility can be increased using alcohol-modified carbon dioxide.
There have not been many applications for the use of water as an additive in the modified mobile phase in SFC compared to bases or acids because, in most cases, the use of additives is usually required for the separation of analytes with basic or acidic forms. The use of water with methanol-modified CO
2 was introduced by Salvador et al. to elute monosaccharides and polyols from silica and trimethylsilyl (TMS)-bonded silica stationary phases in SFC [
12]. Ashraf-Khorassani et al. showed that water was rather useful and superior to formic acid to elute water-soluble nucleobases from polar stationary phases with sharp peaks using a gradient mode of alcohol-modified CO
2 [
13]. Even though these practical improvements of adding water to the mobile phase in SFC are clearly demonstrated, their role in the elution process still needs a dedicated study.
The objective of this work is to figure out how water would influence the methanol adsorption on a hybrid silica column in SFC. For that purpose, two approaches of isotherm adsorption determination were studied: the single-component adsorption isotherm of both methanol and water and the competitive adsorption isotherm of the water–methanol mixture. The mixture composition imitates modifiers and additives that could be used together in the CO2 mobile phase. Furthermore, the band profiles of the studied compounds have been calculated using the parameters acquired from the calculated single-component adsorption isotherms of methanol and water and those parameters obtained from the competitive adsorption isotherm of the water–methanol mixture.
3. Experimental Section
3.1. Chemicals
Carbon dioxide (99.5% from Linde, Répcelak, Hungary), HPLC grade methanol, water, and pentane (VWR International, Fourtenay-sous-Bois, France) were used in this study.
3.2. Instruments
The SFC system used in this study was a Waters UPC
2 system (Waters Corporation, Milford, MA, USA). The system was controlled by Empower v.3 software from Waters as well. The instrument includes a carbon dioxide pump, a modifier pump, an autosampler with a 10 μL sample loop, a 3-column temperature-controlled compartment, a back-pressure regulator, and a diode array UV/VIS detector, which all are in the default configuration. All measurements were performed on a hybrid silica Viridis BEH column (3 × 50) mm packed with 1.7 µm spherical particles, 130 Å pore size from Waters; this Bridged-Ethylene Hybrid (BEH) stationary phase is synthesized by reacting two organosilanes, tetraethoxysilane (TEOS), and 1,2-bis(triethoxysilyl) ethane (BTEE) [
23], as shown in
Figure 1.
A mini-CORI-FLOW mass flow meter from Bronkhorst High-Tech B.V. (Ruurlo, The Netherlands), Model No. M13-ABD-11-0-S was used for measuring CO2 mass flow. The inlet and outlet pressures of the column were measured with an external digital pressure meter (OMEGA Engineering, Norwalk, CT, USA). The density of the mobile phase was calculated using the REFPROP software Ver. 8 from the National Institute of Standards and Technologies (NIST).
3.3. Experimental Conditions
The chromatographic experiments were carried out at 1 mL/min, 26 C, and 150 bar of flow rate, column temperature, and the set value of back pressure, respectively. The injection volume was 1 μL of each pure methanol, pure water, and (10:90 v/v, MeOH:H2O). We chose a high percentage of water with respect to methanol because the corresponding intensity of the water signal of the detector was very small compared to the methanol signal, which was recorded at 195 wavelength. The volume occupied by the mobile phase inside the column is called void volume V0 = 0.242 mL was calculated by determining the retention time of pentane as an unretained solute using 100% CO2, and this retention time was corrected by deducting the required time of the injection profile tsys = 0.07 min.
3.4. Estimation of the Actual Volumetric Flow Rate
The mass flow rate along the chromatographic system is constant under stationary conditions (pressure and temperature). As a result of CO
2 compressibility in SFC—in contrast to the mobile phase in liquid chromatography, which has very limited compressibility—it is necessary to take into account the variation of the volumetric flow rate, which can be substituted by measuring the actual mass flow rate using a Coriolis mass flow meter, which is installed at some point after the CO
2 pump outlet and before the mobile phase mixer. We considered the actual and set flow rates of methanol to be the same. The pressure at the inlet and outlet of the column was measured with an external pressure meter; the values were 184.57 and 154.3 bar, respectively. The density of the mobile phase inside the column was estimated by the REFPROP software Ver. 8 from the National Institute of Standards and Technologies (NIST) at the set temperature of the column 26
C and the measured pressure values of the inlet and the outlet. Using Equation (14), the value of the measured mass flow rate of the mobile phase is
0.943 g/min, and the calculated density of the mobile phase is
0.89891 and 0.87466 g/cm
3 for the inlet and outlet of the column, respectively. We can obtain the average of the two volumetric flow rates as
1.065 mL/min, which is used as the actual volumetric flow rate [
22].
The maximum density of a mobile phase was recorded with 10% methanol in CO2. The percent of density variation along the column was 2.7%. The density of the 100% CO2 mobile phase under the subcritical (26 °C, 145 bar) and the supercritical (40 °C, 250 bar) conditions were 0.875 and 0.887 g/cm3, respectively.
4. Results and Discussion
4.1. Estimation of the Initial Adsorption Isotherm Parameters
The elution profiles of methanol and water recorded at 195 nm wavelength are shown in
Figure 2. The peaks exhibit behavior consistent with the Langmuir adsorption isotherm type. The ECP method has been used to determine the initial parameters of adsorption isotherm for the single component of methanol and water, where the isotherm can be derived from the diffuse part of the elution profile, each point of the rear profile gives one point of the isotherm. The bi-Langmuir Equation (1) has been employed in the ECP method as an adsorption model. The parameter values of the adsorption isotherm of methanol resulting from the ECP method were used as initial values for later calculations. However, the ECP method failed to estimate the isotherm parameters for water adsorption due to the baseline issues with the recorded chromatogram.
4.2. Estimation of the Single-Component Isotherms Using the Inverse Method
The inverse method was applied to the overloaded profiles of both methanol and water eluted from the hybrid silica stationary phase using 100% CO
2 to calculate their single-component adsorption isotherms. As we mentioned in
Section 2.2, the (ED) model was used to calculate the elution profiles. The solution of the (ED) model Equation (4) was calculated using the Rouchon algorithm [
24,
25]. Using the initial bi-Langmuir isotherm parameters obtained by ECP, introducing the column parameters, the overloaded profiles, and the injection profiles in the algorithm, we can simulate the elution profiles. The inverse method can optimize the adsorption isotherm parameters of both studied components using the super-modified simplex algorithm to minimize the differences between the experimental and the calculated elution band profiles.
The simulated and experimental concentration profiles of 1
sample of both methanol and water are overlaid in
Figure 2. From the comparison of the band profiles, we notice a very good agreement between the two profiles at the front part, and even though the late part of the tail does not exhibit a full agreement, the bi-Langmuir model is still a suitable choice to model the adsorption for methanol and water on the hybrid silica column. The single-component bi-Langmuir isotherms determined with the inverse method for both methanol and water are plotted in
Figure 3. The results of the isotherm parameters are summarized in case 1 of
Table 1. The SSR values are an indicator of the goodness of fit.
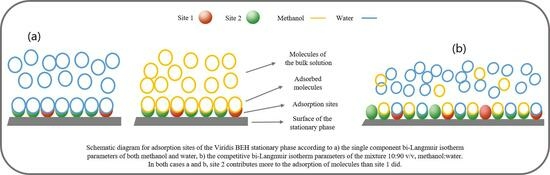
The preliminary results showed that one of the two adsorption sites of the adsorbent has a large saturation capacity for methanol, and the other site also has a large capacity for water, where the curvature of the corresponding isotherms was not observed within the used concentration of the injected sample; hence, it is more feasible to assume those adsorption sites are characterized with a linear isotherm (the parameters for methanol and for water are negligible).
The best-fit parameters of the single-component bi-Langmuir isotherm show that the methanol adsorbs strongly on site 2 with a contribution of 79.5% of the total adsorption (which might be the reason for the tailing peak shape of methanol elution from the column), whereas the site 1 did not reach to the saturation limit, while the adsorption site 1 contributes for retention of water only 16.3%.
Also, it is obvious from the isotherm parameters that the water molecules bind to the site that has a large amount in the stationary phase more than the binding of methanol molecules (
). For the sake of comparison, case 2 (in
Table 1) was suggested, where sites 1 and 2 for water are switched to find out how the simulated band profile in Figure 5 would be affected if the two linear adsorption sites for a studied compound were swapped.
4.3. Competitive Data
We used the inverse method to calculate the adsorption isotherm of the binary mixture of methanol and water on the hybrid silica stationary phase with 100% CO
2; it is assumed that each component of the mixture competes to reach the adsorption sites. It has been discussed that the optimization process of the IM to optimize the adsorption isotherm parameters of both methanol and water requires a concentration profile that can be calculated from the absorbance profile using the linear calibration Equation (12), as we discussed earlier in
Section 2.2.
The recorded data fitted well to the competitive bi-Langmuir model Equation (2), which assumes a heterogeneous surface with two types of non-cooperative independent adsorption sites. The results of fitting the competitive bi-Langmuir model to the experimental chromatogram are summarized in
Table 1. The competitive bi-Langmuir isotherms are shown in
Figure 4.
The results of the competitive isotherm values showed a similar trend to that obtained with the single-component isotherm case, but the saturation capacities () have decreased for the adsorption of both methanol and water in the mixture compared to the single-component sample; hence, this result confirmed the competition between methanol and water to adsorb on the same site.
By comparing the values of the isotherm parameter
(which corresponds to the adsorption site, which has a linear isotherm) for methanol in
Table 1 (7.58, 2.85), we find that the amount of methanol adsorbed in the stationary phase decreases in the presence of water, resulting in a less steep slope (see site 1 in Figs. 3 and 4 (methanol)), which means that the presence of water influences the reduction of methanol adsorption for that site, whereas the slope of the linear adsorption isotherm of water on site 2 did not change notably.
4.4. Prediction of a Band Profile
It is worth performing a simulation of the experimental elution profile to investigate whether the isotherm calculations are reliable. The chromatographic simulation process was carried out with the use of the (ED) model and with the isotherm parameters obtained from (i) the bi-Langmuir isotherm of a single component of methanol and water and (ii) the competitive bi-Langmuir isotherm of the mixture for predicting the elution profile of the (10:90 v/v, methanol:water) mixture sample.
The measured and calculated overloaded band profiles are overlaid in
Figure 5. The simulated band profile, which used the parameter values of the competitive bi-Langmuir isotherm (blue curve), produced remarkably better agreement with the experimental profile (black curve) than those obtained from the parameter values of the single-component isotherms (red and green curves). Although there is a good agreement between the measured and simulated profiles, the rear diffuse part of the calculated band profile has less conformity with the measured profile compared to the front part of the profile.
Figure 6A,B represent the simulated concentration profiles of the individual components of the methanol–water mixture, which corresponds to the simulated absorbance profiles in
Figure 5 with blue and red curves, respectively. It can be noticed from
Figure 6A,B that the concentration peaks of water are larger than methanol peaks, which is contrary to the absorbance peaks in
Figure 5. This might be explained by the different responses of the detector for the two components of the mixture, as it was shown through the detector calibration that we obtained different values of the sensitivity factors:
methanol = 0.208,
water = 0.0048 (see Equation (11)).
5. Conclusions
The adsorption study of both the single-component and the competitive isotherms for methanol and water on a hybrid silica column can be successfully conducted with the inverse method, which requires one sample (injection) for the calculation of each adsorption isotherm in SFC. The (ECP) method was applied to predict the approximate adsorption isotherm parameters value of the studied compounds, wherein it could result in a good estimation for methanol, but it could not give an estimation for water adsorption on the studied column.
The bi-Langmuir model was able to account for the adsorption behavior of the single-component sample of both methanol and water. Also, the competitive bi-Langmuir model was able to represent the adsorption of methanol–water mixture occurring at the equilibrium, which emphasizes the competition between the components of the sample to adsorb on the adsorption sites in the stationary phase resulting in a contribution in the retention process.
The competition occurring between methanol and water of the mixture sample to adsorb on the same adsorption site was clear through the saturation capacity of adsorption sites for the multicomponent system (), which are lower than those for the single-component system.
For calculating the band profile of a mixture sample, we found that employing the parameters of competitive adsorption isotherm in the (ED) model produced a better agreement with the experimental band profile than the parameters of single-component adsorption isotherm.
Understanding the adsorption of methanol and water in a hybrid silica stationary phase from a neat CO2 mobile phase may offer a means for chromatographers to separate hydrophilic compounds using an SFC system in a similar way to hydrophilic interaction liquid chromatography (HILIC) conditions with reduced use of the organic solvents.