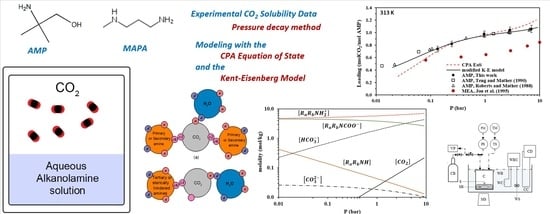
Solubility of CO₂ in 2-Amino-2-methyl-1-propanol (AMP) and 3-(Methylamino)propylamine (MAPA): Experimental Investigation and Modeling with the Cubic-Plus-Association and the Modified Kent-Eisenberg Models

Abstract

CO₂ capture attracts significant research efforts in order to reduce the volume of greenhouse gases emitted from fossil fuels combustion. Among the studied processes, chemical absorption represents a mature approach and, in this direction, new solvents, alternatives to monoethanolamine (MEA), have been suggested. In this work, the solubility of CO₂ in aqueous solutions of 2-amino-2-methyl-1-propanol (AMP) and 3-(methylamino)propylamine (MAPA), which were recently suggested as constituents of novel phase change solvent mixtures, is experimentally measured at 298, 313, 323, and 333 K and in a wide range of pressures, up to approximately 7 bar. As the available literature experimental data for MAPA aqueous solutions are very limited, the experimental results of this study were compared to respective literature data for AMP, and a very satisfactory agreement was observed. The new experimental data were correlated with the cubic-plus-association (CPA) and the modified Kent-Eisenberg models. It was observed that both models rather satisfactorily correlate the experimental data, with the Kent-Eisenberg model presenting more accurate correlations.

1. Introduction

Global temperatures have risen by approximately 1 °C since pre-industrial times [1]. It is believed that greenhouse gases, such as carbon dioxide, nitrous oxide, methane, and others, have a high impact on global warming, and CO₂ emissions due to fossil fuels combustion are considered as the primary anthropogenic contribution factor [2]. They are mainly relevant to power plants, which contribute approximately 40% of the globally emitted CO₂ [3]. The present CO₂ annual emissions are estimated around 36 billion tons, compared to 2 billion tons in 1900 [4], and this figure is projected to drastically increase over the next decades if considerable measures are not taken. Such predicted increase of CO₂ emissions is affected by several factors of high uncertainty, including technological aspects and economic growth, but may be limited by CO₂ climate policies.

In this direction, the CO₂ capture from flue gases has attracted significant research interest, and a variety of processes have been suggested, such as chemical and physical absorption, surface adsorption, chemical looping combustion, membrane separation, cryogenic, and others [5]. The strengths and weaknesses of such processes have been investigated from technical, economic, and social points of view in several studies, as noted in recent review articles [1,2,5]. However, chemical absorption using liquid solvents is considered as the most mature technology, as it is broadly used for removing acid gases form natural gas and can be easily retrofitted onto existing plants [6]. Nevertheless, if applied to existing power plants that utilize fossil fuels, it significantly increases the electricity cost, mainly due to the high energy (heat) demands for the regeneration of the solvent [6,7]. Consequently, increased research efforts have focused on efficient solvent systems, which are alternatives to the conventionally used aqueous monoethanolamine (MEA) solutions, and which include phase change solvents [8], new alkanolamines and their mixtures [9,10], deep eutectic solvents, and ionic liquids [5]. Nevertheless, amines represent the most studied family of solvents for CO₂ capture applications.

CO₂ absorption in aqueous solutions of primary and secondary amines follows two distinct chemical pathways: CO₂ hydration and carbamate formation [11,12]. CO₂ aqueous chemistry can be fully described by the following reactions:

Formation of bicarbonate ion:

$$H_{2}O+C{O}_2\leftrightarrow H^{+}+HC{O}_3^{-}$$

(1)

Dissociation of bicarbonate ion:

$$HC{O}_3^{-}\leftrightarrow H^{+}+C{O}_3^{-2}$$

(2)

Ionization of water:

$$H_{2}O \leftrightarrow H^{+}+O{H}^{-}$$

(3)

The reaction of the first amine molecule ($R_a{R}_{b}NH)$ with $C{O}_2$ results in the formation of a zwitterion intermediate ($R_a{R}_b{N}^{+}HCO{O}^{-})$, which, subsequently, forms a carbamate ($R_a{R}_{b}NCO{O}^{-})$ through the removal of a proton by a second amine molecule. Then, the carbamate can be hydrolized into bicarbonate.

Zwitterion formation:

$$R_a{R}_{b}NH+C{O}_2\stackrel{ }{\leftrightarrow }{R}_a{R}_b{N}^{+}HCO{O}^{-}$$

(4)

Carbamate formation:

$$R_a{R}_{b}NH+R_a{R}_b{N}^{+}HCO{O}^{-}\stackrel{ }{\leftrightarrow }{R}_a{R}_b{N}^{+}{H}_2+R_a{R}_{b}NCO{O}^{-}$$

(5)

Carbamate hydrolysis:

$$R_a{R}_{b}NCO{O}^{-}+H_{2}O\stackrel{ }{\leftrightarrow }{R}_a{R}_{b}NH+HC{O}_3^{-}$$

(6)

The formation of a stable carbamate, which results in low absorption capacity (1 mole of $C{O}_2$ per 2 moles of amine), is mainly dependent on the structure of the amine molecule. In the case of unhindered primary and secondary alkanolamines, such as monoethanolamine (MEA), the carbamate formation is favored because the hydrolysis reaction occurs only to a minor extent. However, the carbamate of hindered amines, such as AMP, is usually unstable and, consequently, the main product is the bicarbonate [13]. Hence, the overall reactions involving unhindered (Equation (7)) and hindered amines (Equation (8)) can be expressed as follows:

Unhindered amines:

$$2R_a{R}_{b}NH+C{O}_2 \stackrel{ }{\leftrightarrow } R_a{R}_{b}N{H}_2^{+}+R_a{R}_{b}NCO{O}^{-}$$

(7)

Hindered amines:

$$R_a{R}_{b}NH+C{O}_2+H_{2}O\stackrel{ }{\leftrightarrow }{R}_a{R}_{b}N{H}_2^{+}+HC{O}_3^{-}$$

(8)

From reactions (7) and (8), it follows that the maximum $C{O}_2$ loading for unhindered amines is stoichiometrically limited to 0.5 mole of $C{O}_2$ per mole of amine, whereas for hindered ones it is equal to 1 mole of $C{O}_2$ per mole of amine. However, despite the fact that sterically hindered primary and secondary amines present higher CO₂ loading values, they usually show lower reaction rates [8,14].

In this work, aqueous mixtures of 2-amino-2-methyl-1-propanol (AMP) and 3-(methylamino)propylamine (MAPA) are investigated. Their structures are shown in Figure 1. AMP is considered as a sterically hindered amine, whereas MAPA is a diamine containing one primary and one secondary amine group. Both were suggested as constituents of novel phase change solvent systems, which usually are aqueous solutions of amine mixtures that exhibit liquid–liquid (VLLE) phase separation upon increase of temperature. The phase split of such solvent systems allows the regeneration of only the CO₂ rich phase, which is usually the aqueous one, resulting in decreased energy demands [8,9,14]. In this direction, Zhang suggested the addition of AMP in a phase change aqueous N,N-dimethylcyclohexyl amine (DMCA)-N-methylcyclohexyl amine (MCA) mixtures [14], as the addition of AMP increases the lower critical solution temperature above 40 °C, without compromising the absorption or desorption performance of the phase-change solvent [14]. Subsequently, the phase behavior of such system was investigated by Tzirakis et al., who also screened the absorption ability of several phase change solvents [15], including aqueous DMCA–MAPA mixtures [16]. However, the most studied MAPA containing phase change solvent is the aqueous DEEA–MAPA system, which was suggested by Pinto et al. [17]. In such solvent systems, ΜAPA is used as an absorption activator, according to the classification suggested by Zhang [14], as it exhibits high CO₂ solubility and fast kinetics.

The use of both AMP and MAPA in novel solvent systems, as well as the suggestion of AMP as potential alternative to MEA, revealed the need for accurate experimental data. The available literature studies containing data for the CO₂ solubility in pure MAPA and AMP aqueous solutions are shown in Table 1 and Table 2, respectively. Nevertheless, the use of both AMP and MAPA in novel solvent systems with a more complex phase behavior (VLLE) than the phase behavior of conventional alkanolamine aqueous solutions (VLE) reveals the need for accurate thermodynamic models that are capable of successful prediction of the phase behavior. This, however, implies the need of accurate experimental data, even on systems containing fewer of the relevant compounds, for the effective parameterization of the models.

The rigorous thermodynamic modeling of such highly non-ideal multicomponent systems requires accounting for all intermolecular interactions, including the ionic interactions among the various species. This can be only performed using electrolyte models, such as the electrolyte EoS/G^E models, or various electrolyte equation of state (EoS) theories, considering also the equilibrium constants of all chemical reactions [18,19,20]. Nevertheless, such an approach presents significant complexity, and usually several simplifications are applied. Considering the use of equation of state models, the most popular simplification is not to explicitly account for chemical interactions, but to effectively account for them through the hydrogen bonding term of the relevant models [9,21,22,23,24]. Such a pseudo-chemical reaction approach was used by Rodriguez et al., who applied the SAFT-VR model to calculate the absorption of CO₂ in aqueous amine solutions [21]. More recently, the SAFT-γ equation of state was used, showing successful predictions for the loading of CO₂ in amine solutions and their phase behavior [9,22]. In the same direction, Tzirakis at al. [24] and Leontiadis et al. [23] used the SRK-CPA EoS, whereas Wang et al. [25] used the PR-CPA, for correlating the solubility of CO₂ in aqueous amine solutions. The thermodynamic routes for modeling the acid gases solubility in aqueous amine solutions were recently reviewed [25].

Table 1. Literature studies reporting experimental data for the CO₂ solubility in aqueous MAPA solutions.

Temperature (K)	Composition	Reference
313, 333, 353, 373	8 m	Chen et al. [26]
313, 353, 393	1, 2 M	Arshad et al. [10]
313, 333, 353, 373	8 m	Voice et al. [27]

Table 1. Literature studies reporting experimental data for the CO₂ solubility in aqueous MAPA solutions.

Temperature (K)	Composition	Reference
313, 333, 353, 373	8 m	Chen et al. [26]
313, 353, 393	1, 2 M	Arshad et al. [10]
313, 333, 353, 373	8 m	Voice et al. [27]

Table 2. Literature studies reporting experimental data for the CO₂ solubility in aqueous AMP solutions.

Temperature (K)	Composition	Reference
313, 393	3 M	Sartori and Savage [13]
313, 373	2, 3 M	Roberts and Mather [28]
323	3.43 M	Teng and Mather [29]
313, 343	2 M	Teng and Mather [30]
293, 313, 333, 353	2, 3 M	Tontiwachwuthikul et al. [31]
301, 303, 313, 323, 333, 343, 353	2 M	Haji-sulaiman and Aroua [32]
303	2 M	Haji-sulaiman et al. [33]
313	2 M	Jane and [34]
313, 333, 353	2.43, 2.44, 2.45, 6.14, 6.24, 6.48 mol/kg	Silkenbäumer et al. [35]
313, 333, 353	30 wt. %	Park et al. [36]
303, 313, 323	2, 2.8, 3.4 M	Kundu et al. [37]
313, 333, 353, 373, 393	3 M	Tobiesen et al. [38]
323	15, 30 wt. %	Arcis et al. [39]
313	3 M	Yang et al. [40]
298, 308, 318, 328	2.5, 3.4, 4.9 mol/dm3	Dash et al. [41]
303, 313, 333	1, 2, 3 M	Sharrif et al. [42]
313, 333, 353, 373	30 wt. %	Tong et al. [43]
313, 333, 363	2 M	Nordin et al. [44]
313, 333, 353, 373	3.4 M, 30 wt. %	Tong et al. [45]
373, 393, 413, 433	4.8 M	Li et al. [46]
313	2.5 M	Nouacer et al. [47]
318	3 M	Kortunov et al. [48]
313, 333, 363	2 M	Narku-Tetteh et al. [49]
313, 333, 353	0.1, 1, 3 M	Hartono et al. [50]

Table 2. Literature studies reporting experimental data for the CO₂ solubility in aqueous AMP solutions.

Temperature (K)	Composition	Reference
313, 393	3 M	Sartori and Savage [13]
313, 373	2, 3 M	Roberts and Mather [28]
323	3.43 M	Teng and Mather [29]
313, 343	2 M	Teng and Mather [30]
293, 313, 333, 353	2, 3 M	Tontiwachwuthikul et al. [31]
301, 303, 313, 323, 333, 343, 353	2 M	Haji-sulaiman and Aroua [32]
303	2 M	Haji-sulaiman et al. [33]
313	2 M	Jane and [34]
313, 333, 353	2.43, 2.44, 2.45, 6.14, 6.24, 6.48 mol/kg	Silkenbäumer et al. [35]
313, 333, 353	30 wt. %	Park et al. [36]
303, 313, 323	2, 2.8, 3.4 M	Kundu et al. [37]
313, 333, 353, 373, 393	3 M	Tobiesen et al. [38]
323	15, 30 wt. %	Arcis et al. [39]
313	3 M	Yang et al. [40]
298, 308, 318, 328	2.5, 3.4, 4.9 mol/dm3	Dash et al. [41]
303, 313, 333	1, 2, 3 M	Sharrif et al. [42]
313, 333, 353, 373	30 wt. %	Tong et al. [43]
313, 333, 363	2 M	Nordin et al. [44]
313, 333, 353, 373	3.4 M, 30 wt. %	Tong et al. [45]
373, 393, 413, 433	4.8 M	Li et al. [46]
313	2.5 M	Nouacer et al. [47]
318	3 M	Kortunov et al. [48]
313, 333, 363	2 M	Narku-Tetteh et al. [49]
313, 333, 353	0.1, 1, 3 M	Hartono et al. [50]

Nevertheless, it was found that empirical approaches, which are considerably simpler, result in very satisfactory correlations for the solubility of acid gases in aqueous amine solutions. The most popular one is probably the Kent-Eisenberg model, which requires knowledge of the equilibrium constants for all chemical reactions [51]. In its original form, the literature values of Henry’s law and ionization constants were used, except from those referring to the amine ionization reaction and the carbamate hydrolysis, which were adjusted to experimental solubility data. The effective values of the adjustable parameters absorb all non-idealities of the system, resulting in very satisfactory results [52]. Consequently, the model found many applications in correlating the acid gases solubility in aqueous amine and alkanolamine solutions and several modifications appeared in literature, which were recently reviewed [53].

In this work, the equilibrium solubility of CO₂ in aqueous AMP (17.7% wt.) and MAPA (30.0% wt.) solutions was experimentally measured, using a pressure decay method, over the temperature range of 298–333 K and CO₂ partial pressures up to approximately 7 bar. The new experimental data for AMP and MAPA were used to parameterize the CPA equation of state model, which was used for the first time to such amine containing systems. The Kent-Eisenberg model was also used to correlate the CO₂ solubility in the aqueous solutions, using new parameters, estimated in this study.

2. Experimental Setup

2.1. Materials

The materials used are shown in

Table 3. Chemicals used in this work.

Product Name	Abbreviation	CAS-Number	Purity	Supplier
Carbon dioxide	CO2	124-38-9	99.9%	Air Liquide
2-Amino-2-methyl-1-propanol	AMP	124-68-5	99.0%	Aldrich
3-(Methylamino)propylamine	MAPA	6291-84-5	97.0%	Sigma-Aldrich
Water	H2O	7732-18-5	HPLC grade	Chem lab

. They were used as received without further purification.

2.2. Experimental Apparatus and Procedure

The applied pressure decay method and the experimental apparatus, which is shown in Figure 2, are described in detail by Leontiadis et al. [23]. The equilibrium cell (high pressure stainless steel with internal volume of 152.2 ± 1.6 cm³ at 25 °C) is equipped with a pressure transducer (WIKA A-10, ±0.5%) and a Pt-100 thermometer (±0.01 K). The cell is immersed into a water bath (model Grant TC-120, temperature stability of 0.1 K). When the entire assembly reaches the desired temperature, a measured (weighted with accuracy of 0.001 g) amount of the solvent is fed into the equilibrium cell, which is evacuated, so the solvent exists under its own vapor pressure. After that, a known (weighted, maximum error ±0.005 g) amount of gas is introduced into the cell using a needle valve. The equilibrium is confirmed when the pressure in the cell remains constant for at least 1 h. At this point the pressure is recorded.

As the CO₂ densities, which were obtained from NIST [54], the total mass of CO₂, the volume of the cell, and the pressure of system are known, the absorbed amount of CO₂ is calculated. According to such procedure, the total pressure of the cell is measured. The CO₂ partial pressure is estimated through subtraction of the solution’s vapor pressure from the total pressure. Such approximation is very often used in similar pressure decay studies [10,23,24,55]. Because the investigated solutions present very low vapor pressures, such correction is insignificant, especially at relatively high pressures (higher than 1 bar).

3. Theory

3.1. The Cubic Plus Association (CPA) Equation of State

The cubic plus association (CPA) equation of state is a combination of a cubic equation of state (the SRK model was used in this study) with the hydrogen bonding term of the SAFT type models that is based on the Wertheim’s first order thermodynamic perturbation theory [56]. In terms of pressure, P, it can be expressed as follows [57,58]:

$$P=\frac{RT}{V_m-b}-\frac{\alpha \left(T\right)}{V_m\left(V_m+b\right)}-\frac{1}{2}\frac{RT}{V_m}\left(1+\rho \frac{\partial lng}{\partial \rho }\right){\displaystyle \sum }_i{x}_i{\displaystyle \sum }_{A_i}\left(1-X_{A_i}\right)$$

(9)

where x_i is the mole fraction of component i and X_Ai is the fraction of the free (not associated with other active sites) A-sites on molecule i, which is related to the association strength Δ^AiBj through the following equation:

$$X_{A_i}=\frac{1}{1+\rho ·{{\displaystyle \sum }}_j{x}_j{{\displaystyle \sum }}_{B_j}\left(X_{B_j}·{\Delta }^{A_i{B}_j}\right)}$$

(10)

The association strength, Δ^AiBj, between two sites, A on molecule i and site B on molecule j, is:

$${\Delta }^{A_i{B}_j}=g\left(\rho \right)\left[exp\left(\frac{{\epsilon }^{A_i{B}_j}}{R·T}\right)-1\right]b_{ij}·{\beta }^{A_i{B}_j}$$

(11)

where $g\left(\rho \right)=1/\left(1-1.9n\right)$ is the radial distribution function, $n=\left(1/4\right)b\rho$ the reduced density, ρ the molar density, ε^AiBj the association energy, β^AiBj the association volume, and $b_{ij}=\left(b_i+b_j\right)/2$. The co-volume parameter, b_i, of component i is considered temperature independent.

A Soave-type relation is used for the interaction energy of the physical term, as follows:

$$a_i\left(T\right)=a_{0,i}{\left[1+c_{1,i}·\left(1-\sqrt{T_{r,i}}\right)\right]}^2$$

(12)

where a₀ and c₁ are pure fluid parameters and T_r is the reduced temperature.

The association energy, ε^AiBj, and the association volume, β^AiBj, that are shown in Equation (11) are only used for associating components, and, along with the three parameters of the physical term (α_ο, b, c₁), are the five pure fluid parameters of the model.

In this study, the conventional mixing rules were used in the physical (SRK) term for the interaction energy and co-volume, using one binary interaction parameter, k_ij, as shown by the next relations:

$$\alpha ={{\displaystyle \sum }}_i{{\displaystyle \sum }}_j{x}_i{x}_j{\alpha }_{ij}, \mathrm{where} {\alpha }_{ij}=\sqrt{{\alpha }_i{\alpha }_j}\left(1-k_{ij}\right)$$

(13)

$$b={\displaystyle \sum }_i{x}_i·b_i$$

(14)

To account for cross association interactions between two self-associating compounds (e.g., between water and amines) the CR-1 rule [59], described by the following relations, was used:

$${\epsilon }^{A_i{B}_j}=\frac{{\epsilon }^{A_i{B}_i}+{\epsilon }^{A_j{B}_j}}{2}, {\beta }^{A_i{B}_j}=\sqrt{{\beta }^{A_i{B}_i}·{\beta }^{A_j{B}_j}}$$

(15)

In addition, the modified CR-1 rule was used to account for cross-association (solvation) interactions between one self- and one non-self-associating fluid [59]:

$${\epsilon }^{A_i{B}_j}=\frac{{\epsilon }^{A_i{B}_i}+{\epsilon }^{A_j{B}_j}}{2}, {\beta }^{A_i{B}_j}={\beta }_{cross}=adjustable$$

(16)

3.2. The Kent-Eisenberg Model

The chemical equilibrium in the systems comprising CO₂, alkanolamines (primary or secondary) and water can be fully described by the following set of reactions [11,12]:

Protonation of amine

$$R_a{R}_{b}N{H}_2^{+}\stackrel{ K_1 }{\leftrightarrow }{R}_a{R}_{b}NH+H^{+}$$

(17)

Hydrolysis of carbamate

$$R_a{R}_{b}NCO{O}^{-}+H_{2}O \stackrel{ K_2 }{\leftrightarrow } R_a{R}_{b}NH+HC{O}_3^{-}$$

(18)

Formation of bicarbonate ion

$$H_{2}O+C{O}_2\stackrel{K_3}{\leftrightarrow }{H}^{+}+HC{O}_3^{-}$$

(19)

Dissociation of bicarbonate ion

$$HC{O}_3^{-}\stackrel{K_4}{\leftrightarrow }{H}^{+}+C{O}_3^{-2}$$

(20)

Ionization of water

$$H_{2}O \stackrel{ K_5}{\leftrightarrow }{H}^{+}+O{H}^{-}$$

(21)

where $R_a{R}_{b}N{H}_2^{+}$ and $R_a{R}_{b}NCO{O}^{-}$ denote the protonated form of the amine ($R_a{R}_{b}NH$) and the carbamate anion, respectively.

The Kent-Eisenberg model sets all activity coefficients equal to unity [51], thus the relevant equilibrium constants are written as follows:

$$K_1=\frac{\left[R_a{R}_{b}NH\right]\left[H^{+}\right]}{\left[R_a{R}_{b}N{H}_2^{+}\right]}$$

(22)

$$K_2=\frac{\left[R_a{R}_{b}NH\right]\left[HC{O}_3^{-}\right]}{ \left[R_a{R}_{b}NCO{O}^{-}\right]}$$

(23)

$$K_3=\frac{\left[HC{O}_3^{-}\right]\left[H^{+}\right]}{\left[C{O}_2\right]}$$

(24)

$$K_4=\frac{\left[C{O}_3^{-2}\right]\left[H^{+}\right]}{\left[HC{O}_3^{-}\right]}$$

(25)

$$K_5=[O{H}^{-}]\left[H^{+}\right]$$

(26)

Henry’s law relates the equilibrium $C{O}_2$ partial pressure to the dissolved $C{O}_2$ concentration $\left(\left[C{O}_2\right]\right)$ in the liquid phase as follows:

$$P_{C{O}_2}=H_{C{O}_2}\left[C{O}_2\right]$$

(27)

Overall mass balances and charge equations can be written as follows:

Amine balance:

$${\left[R_a{R}_{b}NH\right]}_t=\left[R_a{R}_{b}NH\right]+\left[R_a{R}_{b}N{H}_2^{+}\right]+\left[ R_a{R}_{b}NCO{O}^{-}\right]$$

(28)

CO₂ balance:

$${\alpha }_{C{O}_2}{\left[R_a{R}_{b}NH\right]}_t=\left[ R_a{R}_{b}NCO{O}^{-}\right]+\left[HC{O}_3^{-}\right]+\left[C{O}_3^{-2}\right]+\left[C{O}_2\right]$$

(29)

Charge balance:

$$\left[H^{+}\right]+\left[R_a{R}_{b}N{H}_2^{+}\right]=\left[ R_a{R}_{b}NCO{O}^{-}\right]+\left[HC{O}_3^{-}\right]+2\left[C{O}_3^{-2}\right]+[O{H}^{-}]$$

(30)

The equilibrium constants of Equations (22)–(26), the Henry’s law relationship presented in Equation (27), and the material and charge balances (Equations (28)–(30)) can be reduced to a single fifth-order polynomial equation in terms of the concentration of hydrogen ions, $\left[H^{+}\right]$ [60]. Thus, for carbamate forming amine solutions, the following fifth-order polynomial equation is obtained [53]:

$$A{\left[H^{+}\right]}^5+B{\left[H^{+}\right]}^4+ C{\left[H^{+}\right]}^3+ D{\left[H^{+}\right]}^2+E\left[H^{+}\right]+ F=0$$

(31)

where parameters A, B, C, D, E, and F are shown in

Table 4. Parameters of Equation (31).

Parameters
A	1
B	${\left[R_a{R}_{b}NH\right]}_t+K_1$
C 1	$-K_5-K_3\left[C{O}_2\right]+K_C\left[C{O}_2\right]$
D 1	$-K_1{K}_5-2K_3{K}_4\left[C{O}_2\right]-K_1{K}_3\left[C{O}_2\right]-K_C\left[C{O}_2\right]{\left[R_a{R}_{b}NH\right]}_t$
E 1	$-K_C{K}_3{\left[C{O}_2\right]}^2-K_C{K}_5\left[C{O}_2\right]-2K_1{K}_3{K}_4\left[C{O}_2\right]$
F 1	$-2K_C{K}_3{K}_4{\left[C{O}_2\right]}^2$

¹$K_C=K_1{K}_3/K_2$.

.

Only the root with physical meaning, i.e., $pH\in \left[7,12\right]$, is kept from Equation (31) [60]. Then, the CO₂ loading is calculated through the following equations [53]:

$${\alpha }_{C{O}_2}=\frac{\left[C{O}_2\right]+\frac{K_3\left[C{O}_2\right]}{\left[H^{+}\right]}+\frac{K_3{K}_4\left[C{O}_2\right]}{{\left[H^{+}\right]}^2}+\left[ R_a{R}_{b}NCO{O}^{-}\right]}{{\left[R_a{R}_{b}NH\right]}_t}$$

(32)

where:

$$\left[ R_a{R}_{b}NCO{O}^{-}\right]=K_C\frac{\left[C{O}_2\right]}{{\left[H^{+}\right]}^2}\left[\frac{2K_3{K}_4\left[C{O}_2\right]+K_3\left[C{O}_2\right]\left[H^{+}\right]+K_5\left[H^{+}\right]-{\left[H^{+}\right]}^3}{{\left[H^{+}\right]}^2-K_C\left[C{O}_2\right]}\right]$$

(33)

For non-carbamate forming amines, such as AMP, reaction (18) can be neglected because no carbamates are formed. Thus $\left[R_a{R}_{b}NCO{O}^{-}\right]$ is omitted in material and charge balances (Equations (28)–(30)) resulting in the following fourth-order polynomial equation [60]:

$$A{\left[H^{+}\right]}^4+B{\left[H^{+}\right]}^3+ C{\left[H^{+}\right]}^2+ D\left[H^{+}\right]+E=0$$

(34)

where parameters A, B, C, D, and E are shown in

Table 5. Parameters of Equation (34).

Parameters
A	1
B	${\left[R_a{R}_{b}NH\right]}_t+K_1$
C	$-K_5-K_3\left[C{O}_2\right]$
D	$-$2 $K_3{K}_4$[CO2] $-K_1{K}_3$[CO2] $-K_1{K}_5$
E	$-2 K_1{K}_3{K}_4$ [CO2]

.

Consequently, the total CO₂ loading (${\alpha }_{C{O}_2}$) can be calculated through the following equation [53]:

$${\alpha }_{C{O}_2}=\frac{\left[C{O}_2\right]+\frac{K_3\left[C{O}_2\right]}{\left[H^{+}\right]}+\frac{K_3{K}_4\left[C{O}_2\right]}{{\left[H^{+}\right]}^2}}{{\left[R_a{R}_{b}NH\right]}_t}$$

(35)

In both cases, i.e., for carbamate and non-carbamate forming amines, the equilibrium constants $K_i$, as well as the Henry’s law constant, $H_{C{O}_2}$, are estimated through the following empirical relation [53]:

$$ln{K}_i=\frac{A_i}{T}+B_{i}lnT+C_{i}T+D_i$$

(36)

4. Results and Discussion

4.1. Experimental Results

CO₂ loading measurements were performed at 298, 313, 323, and 333 K and various pressures for aqueous solutions that contain AMP (17.7% wt., approximately 2.0 M) and MAPA (30.0% wt., approximately 3.36 M). The obtained experimental data for the AMP and MAPA solutions are presented in

Table 6. CO₂ solubility in 17.7% wt. (2 M) AMP aqueous solutions at 298–333 K ^a.

${\mathit{P}}_{\mathit{C}{\mathit{O}}_2}$ (bar) b	${\mathit{\alpha }}_{\mathit{C}{\mathit{O}}_2}$ (mol CO2/mol AMP)	${\mathit{P}}_{\mathit{C}{\mathit{O}}_2}$ (bar) b	${\mathit{\alpha }}_{\mathit{C}{\mathit{O}}_2}$ (mol CO2/mol AMP)
298.15 K		323.15 K
0.10	0.74 ± 0.05	0.22	0.72 ± 0.05
0.15	0.83 ± 0.04	0.38	0.80 ± 0.05
0.76	1.00 ± 0.05	1.17	0.95 ± 0.05
2.23	1.11 ± 0.05	2.97	1.03 ± 0.05
6.41	1.11± 0.06	7.36	1.05 ± 0.06
313.15 K		333.15 K
0.13	0.74 ± 0.05	0.35	0.71 ± 0.05
0.24	0.82 ± 0.04	0.55	0.78 ± 0.05
0.96	0.97 ± 0.05	1.40	0.92 ± 0.05
2.85	1.04 ± 0.05	3.17	1.02 ± 0.05
7.07	1.06 ± 0.06	7.69	1.04 ± 0.06

^a Standard uncertainty in temperature u(T) = 0.10 K; ^b Standard uncertainty in total pressure u(p) = 0.005∙P.

and

Table 7. CO₂ solubility in 30.0% wt. (3.36 M) MAPA aqueous solutions at 298–333 K ^a.

${\mathit{P}}_{\mathit{C}{\mathit{O}}_2}$ (bar) b	${\mathit{\alpha }}_{\mathit{C}{\mathit{O}}_2}$ (mol CO2/mol MAPA)	${\mathit{P}}_{\mathit{C}{\mathit{O}}_2}$ (bar) b	${\mathit{\alpha }}_{\mathit{C}{\mathit{O}}_2}$ (mol CO2/mol AMP)
298.15 K		323.15 K
0.07	1.00 ± 0.02	0.10	1.00 ± 0.02
0.16	1.10 ± 0.02	0.34	1.09 ± 0.02
0.25	1.14 ± 0.02	0.54	1.12 ± 0.02
0.28	1.17 ± 0.02	0.69	1.15 ± 0.02
0.59	1.22 ± 0.02	1.23	1.18 ± 0.02
0.73	1.26 ± 0.02	1.56	1.21 ± 0.02
0.80	1.25 ± 0.02	1.63	1.20 ± 0.02
1.92	1.34 ± 0.02	3.24	1.27 ± 0.02
3.48	1.43 ± 0.02	5.27	1.34 ± 0.02
4.86	1.47 ± 0.02	6.89	1.37 ± 0.02
313.15 K		333.15 K
0.10	1.00 ± 0.02	0.12	1.00 ± 0.02
0.24	1.10 ± 0.02	0.47	1.08 ± 0.02
0.42	1.13 ± 0.02	0.75	1.11 ± 0.02
0.51	1.16 ± 0.02	0.91	1.13 ± 0.02
1.00	1.19 ± 0.02	1.55	1.17 ± 0.02
1.22	1.23 ± 0.02	1.93	1.19 ± 0.02
1.30	1.22 ± 0.02	1.99	1.18 ± 0.02
2.73	1.30 ± 0.02	3.77	1.24 ± 0.02
4.73	1.36 ± 0.02	5.96	1.30 ± 0.02
6.18	1.40 ± 0.02	7.73	1.33 ± 0.03

^a Standard uncertainty in temperature u(T) = 0.10 K; ^b Standard uncertainty in total pressure u(p) = 0.005∙P.

, respectively. The reported uncertainties in the loading values denote the maximum error, calculated through propagation of errors, considering the uncertainties in the weight of the materials added in the equilibrium cell, in the volume of the cell, in densities, etc.

The new data of this study are illustrated in Figure 3, Figure 4, Figure 5 and Figure 6 and Figure 7, Figure 8, Figure 9 and Figure 10 for AMP and MAPA, respectively. They are compared with available literature experimental data. As it is presented in Figure 3, Figure 4, Figure 5 and Figure 6 and in Table 2, there are some literature experimental data for 2 M aqueous AMP solutions at 313, 323, and 333 K, but it was not possible to find literature data for 298 K. On the other hand, it was not possible to find literature experimental data for 30% wt. aqueous MAPA solutions. Comparisons of Figure 4, Figure 5 and Figure 6 show a rather satisfactory agreement between the new data obtained in this work and the available experimental data from literature.

As shown in Figure 4, the CO₂ loading of the aqueous AMP solutions at 313 K and 0.1 bar, which are the usual conditions of the absorber in the relevant process, is approximately 0.7 mole of CO₂ per mole of amine and reaches a value slightly above 1 mole of CO₂ per mole of amine at higher CO₂ partial pressures. Thus, the obtained experimental data confirm that AMP is performing as a sterically hindered amine, which presents a chemical absorption stoichiometric limit of 1 mole of $C{O}_2$ per mole of amine. However, higher loadings are observed at higher pressures mainly due to physical absorption [14,23]. In addition, as shown in Figure 8, the CO₂ loading of the aqueous MAPA solutions at 313 K and 0.1 bar, is approximately 1 mole of CO₂ per mole of amine. Such loading values are expected, as MAPA molecules consist of two amine groups, one primary and one secondary, each of them presenting a chemical absorption stoichiometric limit of 0.5 moles of CO₂ per mole of amine (group) [8,14,23].

4.2. CPA Modeling Results

As in our previous studies [23,24], the CPA was coupled with the pseudo-chemical reaction approach, i.e., to account for the CO₂–amine chemical interactions as very strong specific interactions. This approximation is often used in equation of state models arising from their inability to explicitly account for chemical interactions [21,22].

Consequently, amine groups, primary and secondary, are modeled assuming that they have one proton donor and one proton acceptor site, which are able to form hydrogen bonds, and one chemical site that can only interact with CO₂. Furthermore, CO₂ is modeled assuming that it has one negative association site that can only interact with water and two (in cases of unhindered primary and secondary amines), or one (in cases of sterically hindered amines) chemical sites that can only associate with the relevant chemical site of the amine groups. In this way, as illustrated in Figure 11, the chemical absorption limit, presented in the Section 1, of 0.5 moles of CO₂ per mole of unhindered primary or secondary amine and of 1 mole of CO₂ per mole of hindered amine is preserved.

The CPA pure fluid parameters for water and CO₂ were adopted from Tsivintzelis et al. [61], whereas the amine parameters were estimated in this study. The AMP molecule, which presents one amine group and one hydroxyl, and the MAPA molecule, which presents two amine groups, one primary and one secondary, were modeled assuming four (equivalent for simplicity) association sites. Thus, the 4C association scheme was used in both cases. Their CPA pure fluid parameters were estimated by adjusting model predictions to available experimental data and/or to DIPRR correlations.

In more detail, the AMP parameters were estimated using the vapor pressure experimental data of Klepacova et al. [62], Barreau et al. [63], Belabbaci et al. [64], and Pappa et al. [65] and the liquid density data from Li and Lie [66]. The MAPA pure fluid parameters were estimated using the vapor pressure data of Kim et al. [67] and the experimental densities of Pinto et al. [68]. All pure fluid parameters used in this study are presented in

Table 8. Pure fluid parameters used in this study.

	a${\mathit{T}}_{\mathit{C}}$ (K)	a0 (L2∙bar∙mol−2)	b (L∙mol−1)	c1	εAiBi (bar∙L∙mol−1)	βAiBi	Association Scheme	Reference
CO2	304.2	3.5079	0.0272	0.7602	-	-	-	Tsivintzelis et al. [61]
H2O	647.3	1.2277	0.0145	0.6736	166.55	0.0692	4C	Tsivintzelis et al. [61]
AMP	619.8 b	19.6710	0.0882	0.9050	162.24	0.0087	4C	This study
MAPA	601.9 c	18.2771	0.0929	1.0732	86.64	0.0557	4C	This study

^a T_c: critical temperature, ^b Predicted (DIPPR), ^c Estimated with Constantinou Gani [69] group contribution method.

. In all cases, model correlations present low absolute average deviations (AAD) for the used data, i.e., 0.14% and 1.53% for the AMP vapor pressures and molar volumes, respectively, and 1.52% and 0.37% for MAPA vapor pressures and molar volumes, respectively. The obtained CPA correlations are illustrated in Figures S1–S4 of the supplementary information file.

The used binary parameters are presented in

Table 9. CPA binary parameters used in this study.

	kij	εcross (bar∙L∙mol−1)	βcross	εcross (bar∙L∙mol−1)	βcross
CO2–water	0.11406 a	Exp. 142.0 a	mCR1: 0.0162 a	-	-
AMP–water	−0.0325	CR-1	CR-1	-	-
MAPA–water	−0.3364	CR-1	CR-1
CO2–AMP	−0.1780	318.9	0.02184	-	-
CO2–MAPA	0.3310	435.3	0.0005	311.9	0.002

^a CO₂-H₂O adopted from Tsivintzelis et al. [61].

. Such parameters for the CO₂–water sub-binary system were adopted form Tsivintzelis et al. [61], who suggested modeling CO₂–water interactions assuming one association site on CO₂ molecule, which is able to cross associate with water, while using the experimental value for the cross association energy. The binary interaction parameter, k_ij, for the AMP–water sub-binary system was estimated using the vapor–liquid equilibrium (VLE) experimental data of Pappa et al. [65]. It was found that, when using the CR-1 combining rule for the cross association interactions, the model satisfactorily describes the VLE of this system as shown in Figure S5 of the supplementary information file. For MAPA–water sub-binary systems, the experimental data of Kim et al. [67] for 373 K were used, and representative calculations are illustrated in Figure S6 of the supplementary information file.

Finally, the parameters for CO₂–amine sub-binary systems were estimated by adjusting model predictions to the experimental data of this study. In all cases, a temperature independent k_ij was used. Considering the CO₂–AMP system, it was found that the cross association energy of 318.9 bar∙L∙mol⁻¹, reported for CO₂–DETA and CO₂–TETA systems in a previous study [24], gives rather satisfactory results and was also adopted for this system. For the same reason, the cross association energies used for CO₂–MPA by Leontiadis et al. [23] were also adopted for the CO₂–MAPA interactions. Such results indicate that, probably, universal parameters for the CO₂–amine interactions can be estimated within the CPA model. Thus, in both cases only the cross association volumes were adjusted to the experimental data. All CPA calculations are presented in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 and shown in

Table 10. Percentage average absolute deviations (AAD %) of models’ correlations form the experimental data of this study for the CO₂ loading of AMP solutions.

Composition (M)	Temperature (K)	No. of Data Points	CPA AAD %	K-E Model AAD %
2	298.15	5	33.9	6.8
2	313.15	5	18.1	1.7
2	323.15	5	14.1	2.1
2	333.15	5	14.7	4.0
		Total	20.2	3.7

and

Table 11. Percentage average absolute deviations (AAD %) of models’ correlations form the experimental data of this study for the CO₂ loading of MAPA solutions.

Composition (M)	Temperature (K)	No. of Data Points	CPA AAD %	K-E Model AAD %
3.35	298.15	10	26.2	1.5
3.35	313.15	10	22.1	1.2
3.35	323.15	10	20.2	0.7
3.35	333.15	10	28.7	0.5
		Total	24.3	1.0

; the percentage AADs of CPA correlations from the experimental data are 20.2 and 24.3% for AMP and MAPA solutions, respectively. Such rather high deviations are mainly observed due to the severe pseudo-chemical association approach, which, however, is necessary in such EoS models.

It is worth noting that using the CPA model, seven adjustable parameters were used for modeling the solubility of CO₂ in aqueous MEA solutions and five parameters for aqueous MDEA solutions by Wang et al. [25], whereas Leontiadis et al. [23] used six parameters for CO₂–MPA and four binary parameters for CO₂–MDEA pseudo-chemical interactions. Finally, Tzirakis et al. [24] used four adjustable parameters for CO₂–DETA and CO₂–TETA interactions. The rather high number of the parameters that need to be adjusted and the rather high value of the obtained k_ijs mainly occur due to the severe approximation of the pseudo-chemical reaction approach.

4.3. Kent-Eisenberg Model Results

As noted in the Section 1, AMP is sterically hindered and, thus, it is considered as a non-carbamate forming amine. Consequently, reaction (18) is not accounted for and Equations (34)–(36) are used to apply the Kent-Eisenberg model. On the other hand, MAPA is a diamine, consisting of a primary and a secondary amine group. In order to minimize the need for adjustable parameters, MAPA was modeled assuming equal and independent reactivity for each amine group, i.e., that the reactivity of each group does not depend on the potential reaction of the other one. This approximation was also used by Tzirakis et al. [70] to model the CO₂ solubility in aqueous solutions of diamines. It resembles the Flory’s principle of independent reactivity, according to which the reactivity of each group is independent of the polymer chain length and is considered as a very good approximation for molecules (oligomers) with higher than 3–5 carbon atoms. Thus, MAPA was modeled using Equations (31)–(33). However, using the aforementioned approximation, all amine species concentrations shown in Equations (17)–(33) will denote moles of amine groups and not moles of molecules. In addition, the calculated loading from Equation (32) will denote the moles of absorbed CO₂ per mole of amine groups (not molecules) and should be multiplied by two to be compared with the experimental results (which show moles of CO₂ per mole of amine molecules).

In this work, we have decided to use the literature values of the parameters of Equation (36) for $K_3$ through $K_5$ and $H_{{CO}_2}$. Consequently, only the parameters of Equation (36) for $K_1$ and $K_2$ were adjusted to the experimental data of this work and to literature data (presented in Tables S1 and S2 of the supplementary information file, for AMP and MAPA solutions, respectively). All the available literature data points within the temperature range of 313 to 383 K and pressure range of 0.1 to 10 bar, plus the data of this work were included and equally weighted in the objective function. All the used parameters, obtained from literature or regressed in this work, for AMP and MAPA solutions are listed in

Table 12. Parameters of Equation (36) for AMP and MAPA aqueous solutions.

Parameter (T in K)	Units	A	B	C	D	Regression Range (K)	Reference
$K_{1 AMP}$	$\mathrm{mol}/\mathrm{kg}$	−5936.63	0	0	−3.1347	313–383	This work
$K_{1 MAPA}$	$\mathrm{mol}/\mathrm{kg}$	−6164.85	0	0	−4.1080	313–383	This work
$K_{2 MAPA}$	$\mathrm{mol}/\mathrm{kg}$	−3534.70	0	0	7.4398	313–383	This work
$K_3$	$\mathrm{mol}/\mathrm{kg}$	−12,092.10	−36.7816	0	235.482	273–498	Edwards et al. [71]
$K_4$	$\mathrm{mol}/\mathrm{kg}$	−12,431.70	−35.4819	0	220.067	273–498	Edwards et al. [71]
$K_5$	$\mathrm{mol}/\mathrm{kg}$	−13,445.90	−22.4773	0	140.932	273–498	Edwards et al. [71]
$H_{C{O}_2}$	$\mathrm{atm} \mathrm{mol}/\mathrm{kg}$	−6789.04	−11.4519	−0.010454	94.4914	273–498	Edwards et al. [71]

.

Using the parameters of Table 12, model-predicted CO₂ loadings were compared to the experimental data of this work. The results for 2 M AMP and 3.35 M MAPA aqueous solutions are illustrated in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 and, as parity plots, in Figures S7 and S8 of the supplementary information file. The obtained deviations of model correlations from the experimental data of this work are shown in Table 10 and Table 11, for AMP and MAPA solutions, respectively. In more detail, using two parameters adjusted to the experimental data (A and D parameters of Table 12 for K_{1 AMP}), the model presents an overall percentage average deviation from the experimental data of this study equal to 3.7%. Using two additional adjustable parameters for MAPA (A and D parameters of Table 12 for K_{1 MAPA} and K_{2 MAPA}), the observed deviations are significantly lower and equal to 1%. Such rather low deviations reveal that the model, although very approximate, allows the correct description of the experimental data if appropriate values of the adjustable parameters are selected, i.e., effective values that, according to Jou et al. [52], absorb all non-idealities of the system. Compared to the CPA EoS, it presents significantly more accurate correlations, however, using more adjustable parameters.

Because the modified Kent-Eisenberg model resulted in more accurate correlations, it was subsequently used to predict the speciation of the loaded liquid phase for both amine systems. Results for 313 K are presented in Figure 12 and Figure 13, whereas the other investigated temperatures are shown in Figures S9–S14 of the supplementary information file. It is observed that the free amine concentration becomes very low at CO₂ partial pressures higher than approximately 1 bar, whereas at higher CO₂ partial pressures, the increase of the overall CO₂ solubility mainly proceeds through the molecular CO₂ dissolution, as shown by the respective molecular CO₂ curve of Figure 12 and Figure 13, and the carbamate hydrolysis, in the case of MAPA, as shown by the RRNCOO⁻ curve in Figure 13.

5. Conclusions

In this study, the solubility of CO₂ in 17.7% wt. (approximately 2M) aqueous 2-amino-2-methyl-1-propanol (AMP) and 30.0% wt. (approximately 3.36 M) 3-(methylamino)propylamine (MAPA) solutions was experimentally measured, in the 298–333 K temperature range, using a pressure decay method. Because the available literature experimental data for MAPA aqueous solutions are very limited, the experimental results of this study were compared to respective literature data only for AMP aqueous systems, and a rather satisfactory agreement was observed. Such experimental data are useful in parameterizing thermodynamic models. Consequently, they were used to parameterize the CPA equation of state coupled with the pseudo-chemical reaction approach, which is a severe, but necessary, approximation in order to apply such thermodynamic models, and the modified Kent-Eisenberg model, which is an approximate semi-empirical model. It is observed that the modified Kent-Eisenberg model correlations present a very satisfactory agreement with the experimental data. Compared to the CPA EoS, the Kent-Eisenberg model presents significantly more accurate correlations, but at the cost of more adjustable parameters. Considering also its low complexity compared to association models, it could be a rather satisfactory choice if, other than the CO₂ solubility, no other thermodynamic properties are needed. However, if other properties, such as densities of phases in equilibrium or thermal properties, are needed in engineering design applications, the choice of a thermodynamic model, such as an equation of state model, is mandatory.